VIO第二讲
Source
Edit
History

第二讲_IMU相关内容

1. 第二讲_IMU相关内容

1.1. 旋转运动学

1.1.1. 运动半径\(r\)对\(\theta\)的求导,再写成矩阵形式

\(\color{red}{下图中:半径a和高度h固定}\)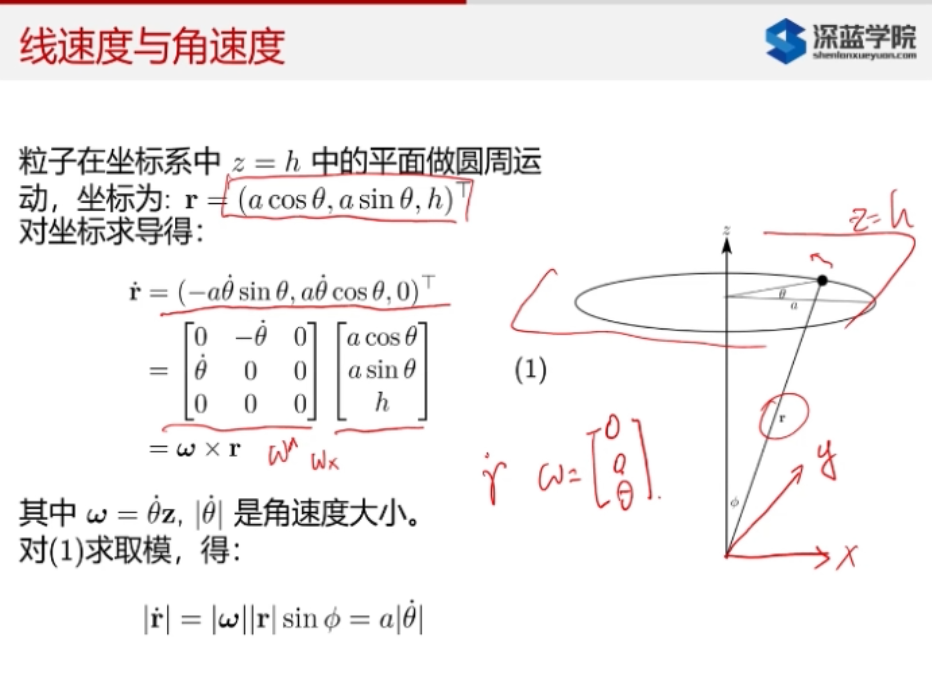

从结果可以看到,矩阵形式的导数表示可以写成矩阵形式\(\omega \times r\),左侧为反对称矩阵w

1.1.2. 考虑更复杂的情况,假设旋转坐标系下的情况

1.1.2.1. 旋转坐标系下的运动学(暂时不考虑平移)

考虑两个坐标系,一个静止的坐标系,惯性坐标系i系,另外一个是旋转的坐标系即载体坐标系b系.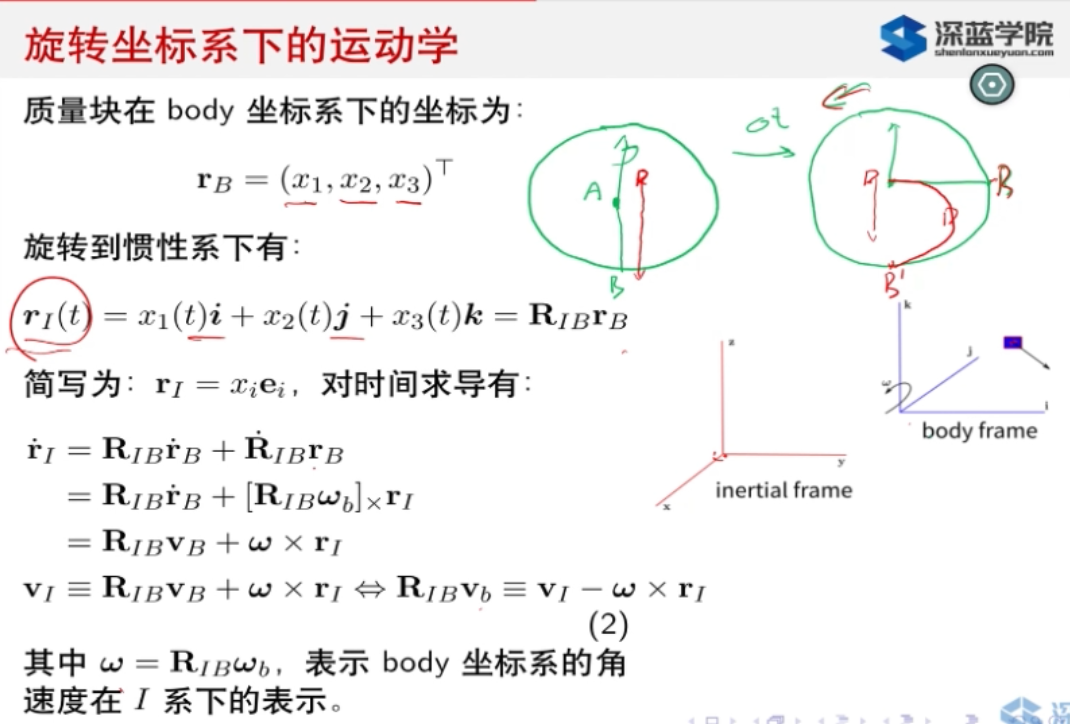

其中,关于旋转矩阵\(R_{IB}\)的导数\(\dot{R_{IB}}\)可看第一讲的内容. > 结果:一个有趣的现象是,物体在惯性系下的速度\(\dot{r}\)并不是直接等于物体在b系下的速度乘以旋转矩阵\(R_{IB}*v_{B}\),后面还多了一项\(-\omega \times r_I\),这就是哥氏加速度带来的影响.

* 补充: * \(\dot{R}_{IB}r_B=\omega \times r_I\)的详细证明 (1)用到了性质\(R[a]_\times=[Ra]_\times R\) (2)用到了性质\(\dot{R}=R\omega\) \[ \begin{aligned} \dot{R}_{IB}r_B &= \lim_{\Delta t \to 0} \frac{R_{IB} \exp([\omega_{BB'} \Delta t]\hat{~})r_B-R_{IB}r_B}{\Delta t} \\ &= \lim_{\Delta t \to 0} \frac{R_{IB} (I+[\omega_{BB'}\Delta t]\hat{~}) r_B-R_{IB}r_B}{\Delta t} \\ &= \lim_{\Delta t \to 0} \frac{R_{IB} [\omega_{BB'}\Delta t]\hat{~} r_B}{\Delta t} \\ &= \lim_{\Delta t \to 0} \frac{-R_{IB} r_B\hat{~} (\omega_{BB'}\Delta t)}{\Delta t} \\ &= {-R_{IB} r_B\hat{~} (\omega_{BB'})} \\ &= R_{IB}(\omega_{BB'})\hat{~}r_B \\ &=[R_{IB}\omega_{BB'}]_\times R_{IB}r_B \\ &=\omega \times r_I \end{aligned} \]

  • 关于速度的求导部分的补充
  • 因为有\(\dot{R_{IB}}=R_{IB}[\omega_b]_\times =[R_{IB}\omega_b]_\times R_{IB}\)(根据性质-第一讲)
  • 所以\(\dot{R_{IB}}v_b=R_{IB}[\omega_b]_\times v_b=[R_{IB}\omega_b]_\times R_{IB} v_{b}=\omega \times v\)
  • \(\dot{R_{IB}}\omega_b=R_{IB}[\omega_b]_\times \omega_b=R_{IB} \omega_b \hat{~}\omega_b=0\)

结果:结果表明,物体在惯性系的加速度a_i并不直接等于b系下的加速度乘以对应的旋转矩阵,而是要加上后面几项,其中,哥氏力是成对出现的,另外:由于w_{ie}为常量,所以\(\omega\)求导后的\(\dot{\omega}\)为0,所以一般欧拉力为0?.

1.2. IMU测量模型和运动模型

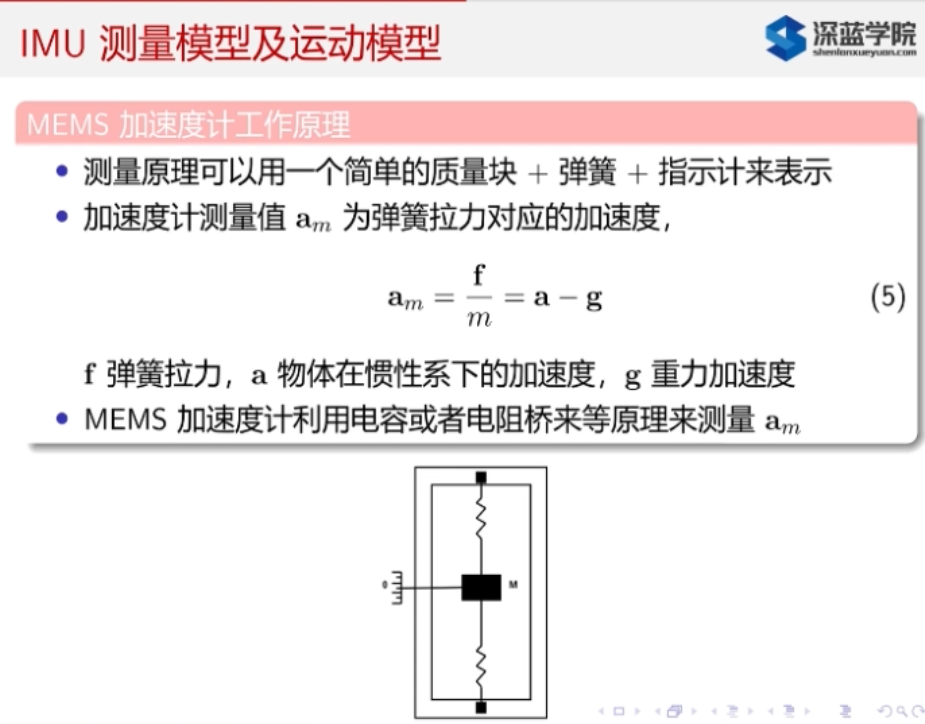
1.2.1. 加速度测量

1.2.2. 角速度测量

主要利用科氏力来计算角速度

1.3. IMU误差模型

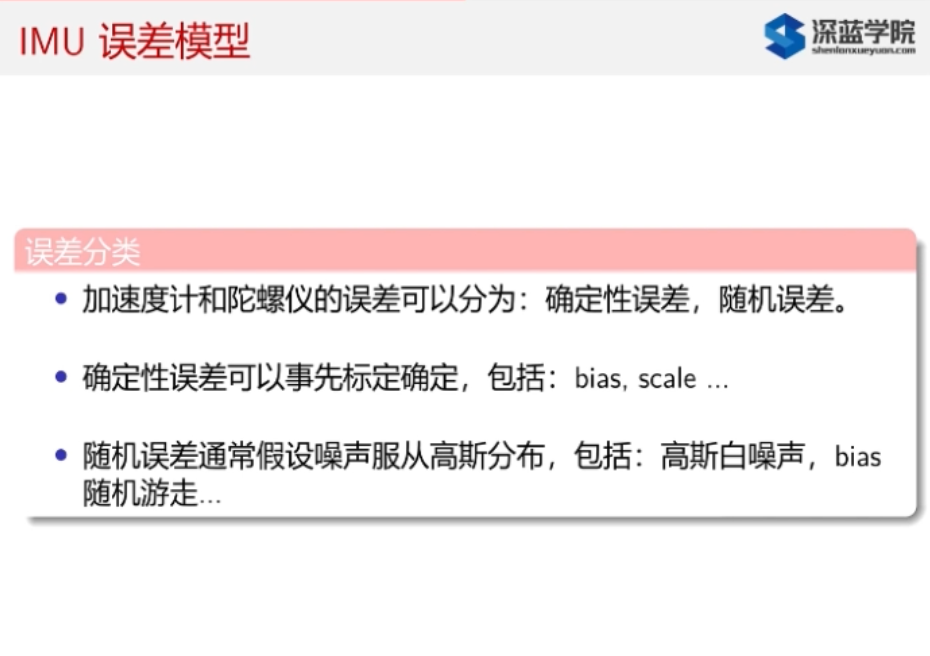
1.3.1. 确定性误差

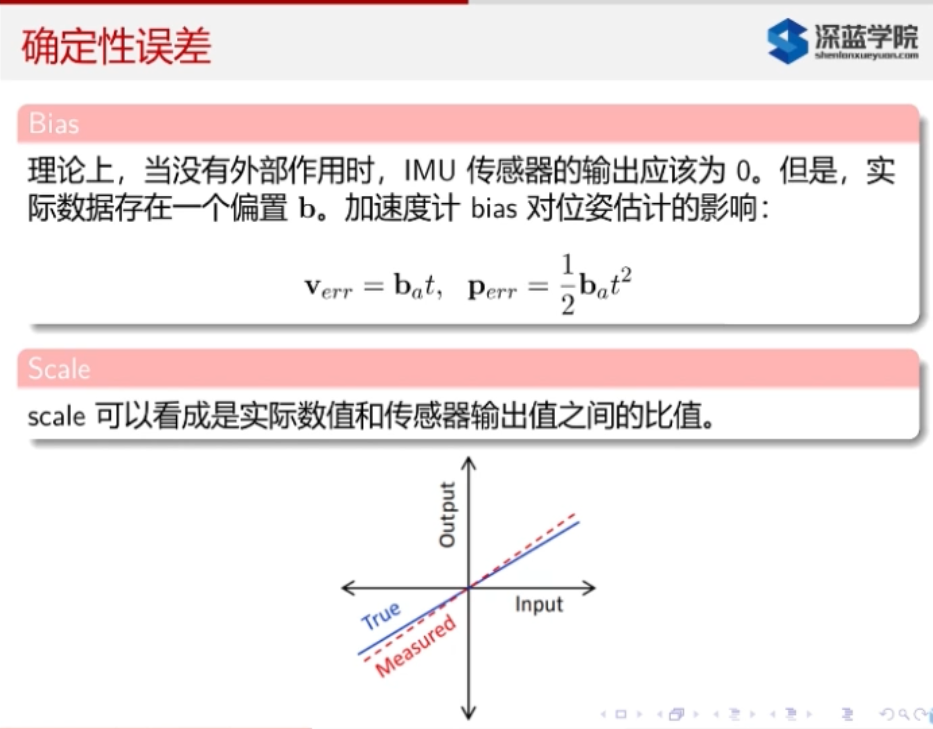
* run-to-run : 每次上电的时候的bias叠加 * run-in-run : 每次上电时候的bias不一样 * 温度

1.3.2. 标定方法

1.3.2.1. 加速度计标定

1.3.2.2. 陀螺仪标定

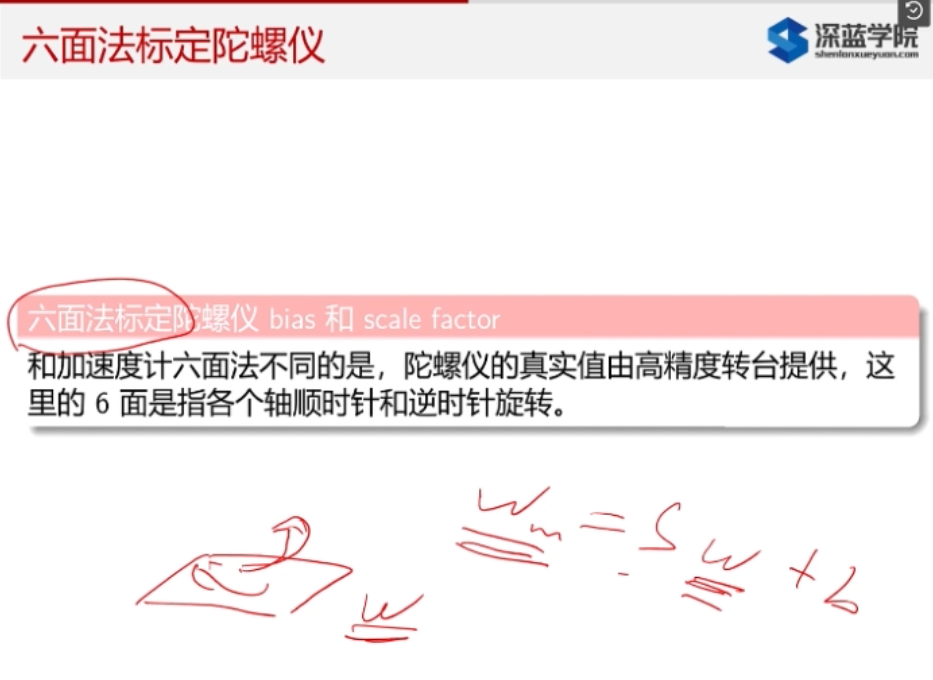
1.3.2.3. 温度相关系数

1.3.2.4. 不确定性误差(随机误差)

1.3.2.5. Bias误差模型

1.3.2.6. 艾伦方差标定(常用)

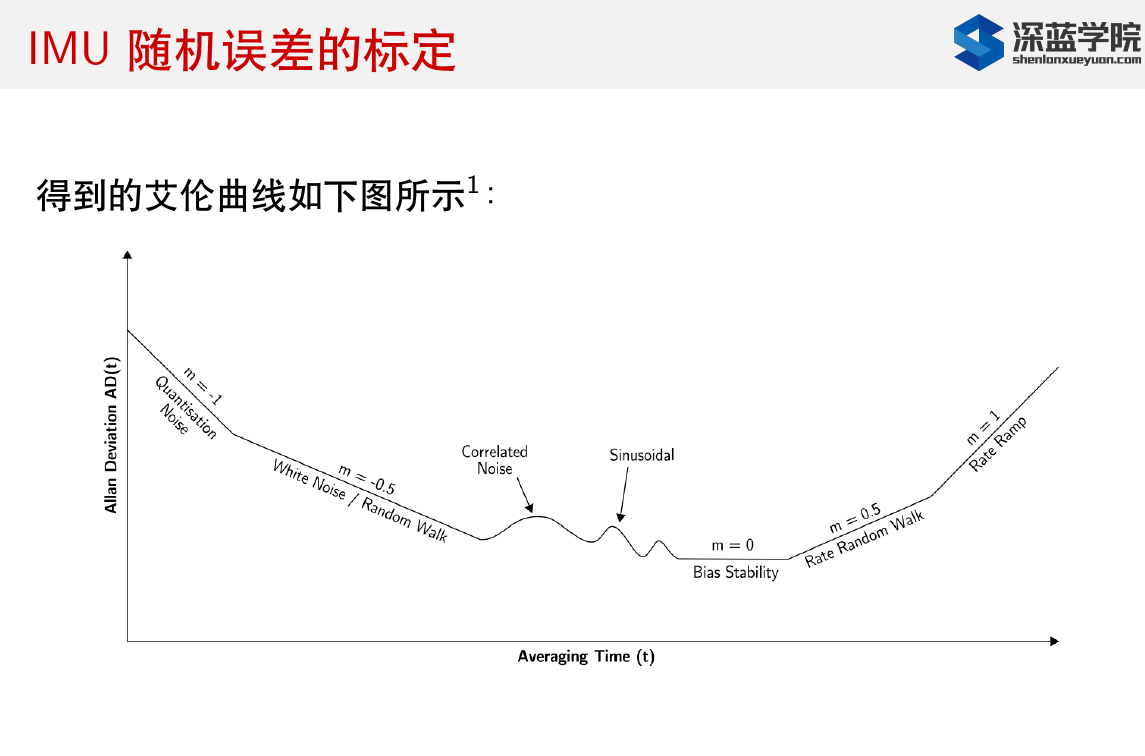* 使用标定工具 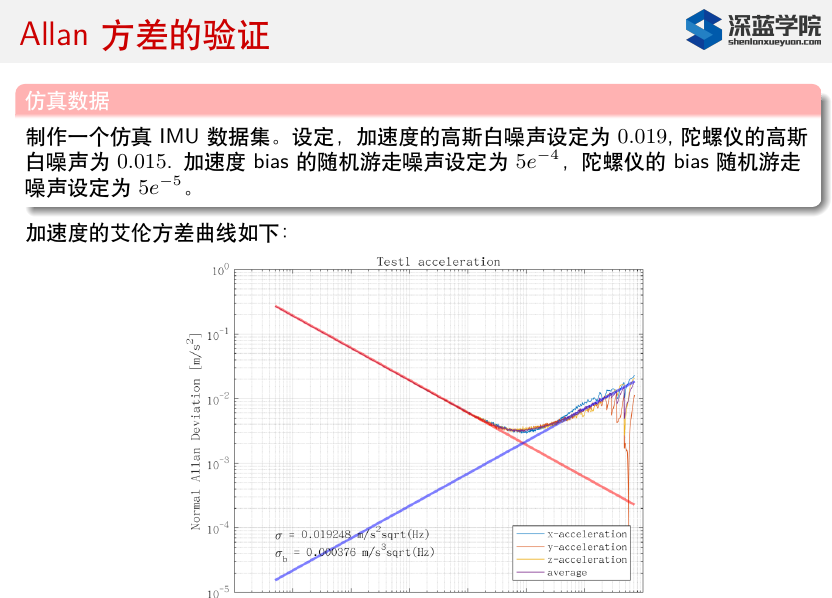* 美国:calibration alan * 港科大:imu_utils

1.3.2.7. 加速度计数学模型

1.3.2.8. 陀螺仪数学模型

  • 1.4. 运动模型离散时间处理

1.4.1. 欧拉法

关于姿态q的离散积分: \[ \begin{aligned} \because \dot{q}_{wb_k}=q_{wb_k} \otimes [0,\frac{1}{2}\omega]^T \end{aligned} \]

\[ \begin{aligned} \therefore q_{wb_{k+1}}&=q_{wb_k}+\dot{q}_{wb_k} \delta t \\ &= q_{wb_k}+q_{wb_k} \otimes [0,\frac{1}{2}\omega]^T \\ &=q_{wb_k} \otimes [1,\frac{1}{2}\omega]^T \end{aligned} \]

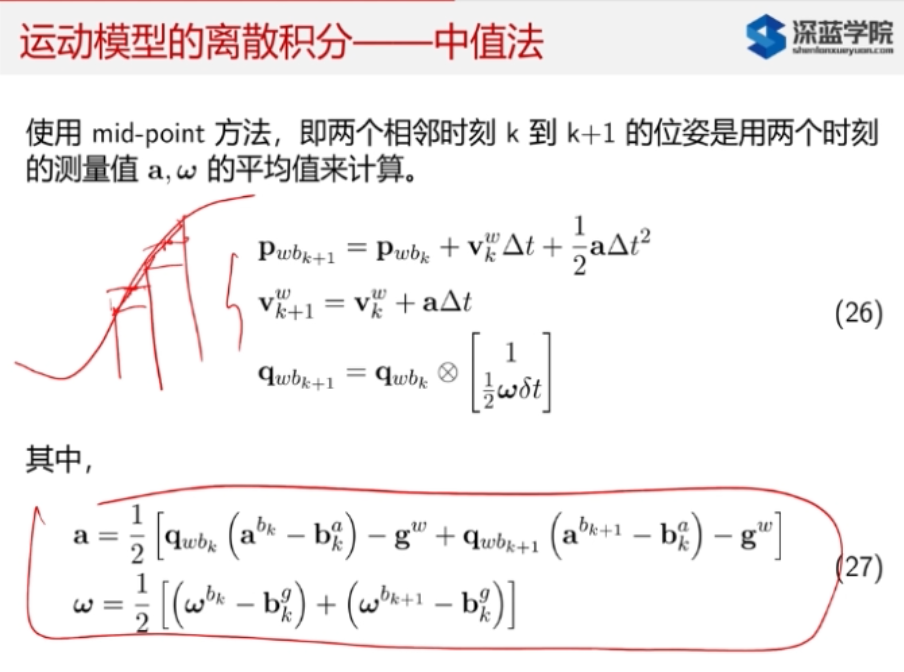
1.4.2. 中值法

比欧拉法稍微精确一点

-- ## 1.5. 仿真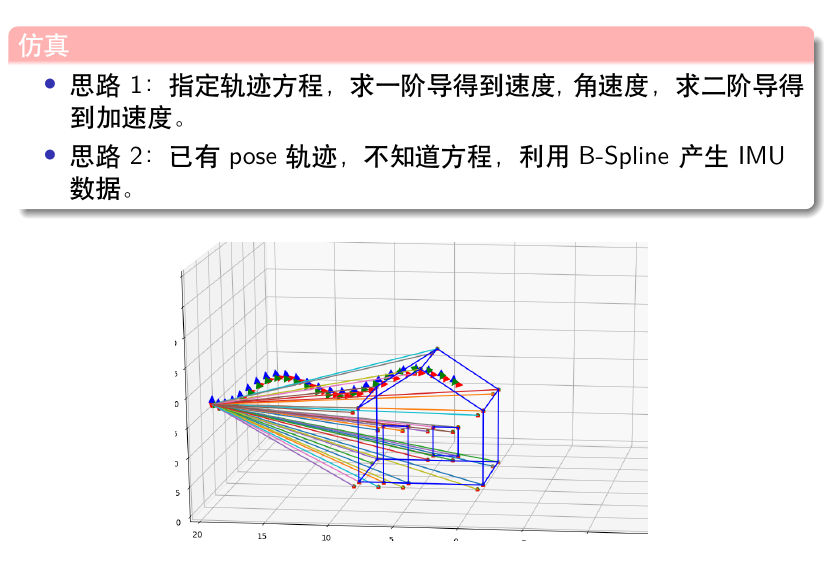

1.5.1. 知识补充

\(\color{red}{注意欧拉角(3维向量)形式的旋转积分:需要先使用旋转矩阵将b系下的角速度转换为世界坐标系的欧拉角速度}\)

1.5.2. 个人理解

上面的关于欧拉角旋转的描述是基于ZYX321顺序的,其对应的坐标系是前右下,对应的导航坐标系是北东地,常用于无人机.下面用另外一种欧拉角顺序推导一遍,该顺序更常用于地面无人车.

1.5.2.1. 方向余弦矩阵的基本形式

一个向量的方向（姿态）我们可以用他在参考坐标系（地理坐标系）各个轴向的夹角的余弦来表示（及在各个轴的投影）。 类似的 一个坐标系 可以看成是3个向量组成，所以三个向量分别在坐标轴上的投影可以用来表示一个坐标系与参考坐标系的关系。这总共9个方向余弦组成了一个三阶矩阵，其对应方式如下图。 \[ \quad C_b^n= \begin{bmatrix} c_{11} & c_{12} &c_{13} \\ c_{21} & c_{22} &c_{23} \\ c_{11} & c_{12} &c_{13} \end{bmatrix} \quad \] 其中，第 i 行、 j 列的元素表示参考坐标系 i 轴和姿态坐标系 j 轴夹角的余弦。事实上方向余弦和欧拉角没有本质区别，因为方向余弦实际上就是用欧拉角表示的。

1.5.2.2. 方向余弦矩阵的举例推导

一个二维的坐标变换如下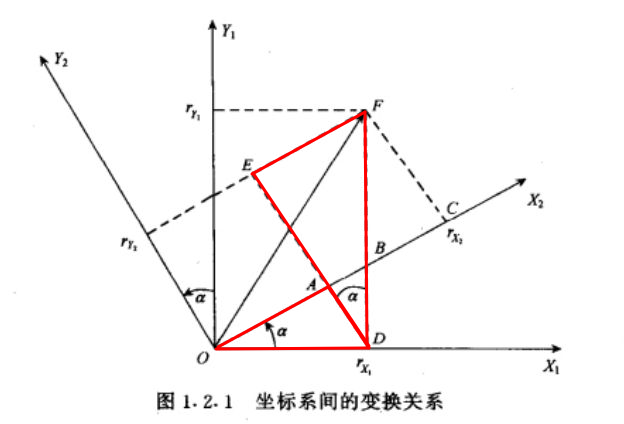： 点F为固定点，在坐标系1下的表示为\(F(r_{x1},r_{y1})\)，在坐标系2下为\(F_{2}(r_{x2},r_{y2})\) 由图可知,注意观察使用图中两个红色的三角形 \[ \begin{aligned} r_{x2}&=r_{x1}*\cos \alpha+ r_{y1}*\sin \alpha \\ r_{y2}&=r_{x1}*(-\sin \alpha)+r_{y1}*\cos \alpha \end{aligned} \] 推广到三维的情况下，可看作是绕Z轴逆时针旋转，并写成矩阵形式： \[ \quad \begin{bmatrix} r_{x2} \\ r_{y2} \\ r_{z2} \end{bmatrix}= \begin{bmatrix} \cos \alpha & \sin \alpha &0 \\ -\sin \alpha & \cos \alpha &0 \\ 0 & 0 &1 \end{bmatrix} \begin{bmatrix} r_{x1} \\ r_{y1} \\ r_{z1} \end{bmatrix} \quad \] 由上面的例子，可推理余弦矩阵各个元素的意义 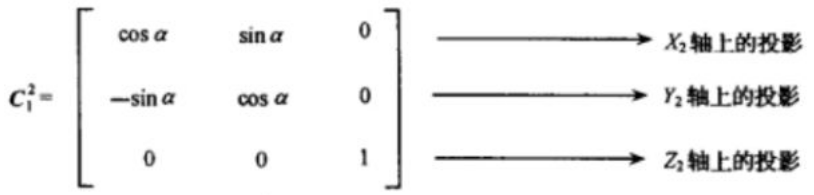* 第1行表示旋转之后的X2轴在原坐标系(X1,Y1,Z1)轴下的投影 * 第2行表示旋转之后的Y2轴在原坐标系(X1,Y1,Z1)轴下的投影 * 第3行表示旋转之后的Z2轴在原坐标系(X1,Y1,Z1)轴下的投影

1.5.2.3. 东北天ENU---->右前上的余弦矩阵\(C_{n}^{b}\)推导

假设我们现在有一个东北天坐标系和一个载体坐标系，现需要将东北天坐标系经过3次旋转，使得最终得到的坐标系与载体坐标系重合。 > 在此之前，需要做出一些规定 > * 旋转的正方向为：从旋转轴看的逆时针方向 > * 旋转的顺序为：Z-X-Y > * 对应的欧拉角：Yaw-Pitch-Roll

1.5.2.3.1. 绕Z轴逆时针旋转\(\psi\)——Yaw

得到旋转矩阵\(C_{n}^{1}\) \[ \quad C_{n}^{1}= \begin{bmatrix} \cos \psi & \sin \psi &0 \\ -\sin \psi & \cos \psi &0 \\ 0 & 0 &1 \end{bmatrix} \quad \]

1.5.2.3.2. 绕X'轴逆时针旋转\(\theta\)——Pitch

得到旋转矩阵\(C_{1}^{2}\) \[ \quad C_{1}^{2}= \begin{bmatrix} 1 & 0 &0 \\ 0 &\cos \theta & \sin \theta \\ 0 &-\sin \theta & \cos \theta \end{bmatrix} \quad \]

1.5.2.3.3. 绕Y''轴逆时针旋转\(\phi\)——Roll

得到旋转矩阵\(C_{2}^{3}\) \[ \quad C_{2}^{3}= \begin{bmatrix} \cos \phi & 0 &-\sin \phi \\ 0 & 1& 0 \\ \sin \phi & 0& \cos \phi \end{bmatrix} \quad \]

1.5.2.3.4. 得到ENU导航坐标系到右前上载体坐标系的方向余弦矩阵\(C_{n}^{b}\)

\[ \begin{aligned} C_{n}^{b}=&C_{2}^{3}C_{1}^{2}C_{n}^{1} \\ =& \begin{bmatrix} \cos \phi & 0 &-\sin \phi \\ 0 & 1& 0 \\ \sin \phi & 0& \cos \phi \end{bmatrix} \begin{bmatrix} 1 & 0 &0 \\ 0 &\cos \theta & \sin \theta \\ 0 &-\sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} \cos \psi & \sin \psi &0 \\ -\sin \psi & \cos \psi &0 \\ 0 & 0 &1 \end{bmatrix} \\ =& \begin{bmatrix} \cos \psi \cos \phi -\sin \psi \sin \theta \sin \phi & \sin \psi \cos \phi+\cos \psi \sin \theta \sin \phi & -\cos \theta \sin \phi \\ -\sin \psi \cos \theta & \cos \psi \cos \theta & \sin \theta \\ \cos \psi \sin \phi+ \sin \psi \sin \theta \cos \phi & \sin \psi \sin \phi- \cos \psi \sin \theta \cos \phi & \cos \theta \cos \phi \end{bmatrix} \\ = & \begin{bmatrix} c_{11} & c_{12} &c_{13} \\ c_{21} & c_{22} &c_{23} \\ c_{11} & c_{12} &c_{13} \end{bmatrix} \end{aligned} \]

1.5.2.4. \({\color{red}{(ZXY-312顺序)欧拉角微分}}\)

上面的方向余弦矩阵\(C_n^b\)描述了将一个点.

1.5.2.5. 导航坐标系下欧拉角离散积分形式推导

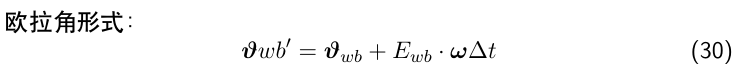
\(\because\)欧拉角形式积分: \(\vartheta_{wb'}=\vartheta_{wb'}+ \frac{d \vartheta}{dt} \Delta t\).用到了欧拉角的微分形式 \(\therefore\)需要求\(\frac{d \vartheta}{dt}\) 其中: (1)\(\vartheta=[\theta_{pitch},\Phi_{roll},\psi_{yaw}]^T\)表示在导航坐标系下的欧拉角速度 (2)\(\omega\)表示在载体坐标系b系下的三个角速度 求:利用\(\omega\)表示出导航坐标系下的欧拉角微分\(\frac{d \vartheta}{dt}\)

求解: 以下部分参考来自:<欧拉角微分方程推导> >1. 假设已经完成绕三个轴的旋转，则最后绕Y轴的角速度在载体坐标系和导航坐标系都是一样的，所以有如下公式： \[ \begin{aligned} \omega_b(roll)=\begin{bmatrix} 0\\ \frac{d roll}{dt} \\ 0 \end{bmatrix} \\ \end{aligned} \] >2. 假设已经完成了前两组旋转，最后一组旋转没有完成，如果接着完成最后一步旋转，则和第一步一样，绕X轴的角速度在两个坐标系下是一样的，则有如下公式： \[ \begin{aligned} \omega_b(pitch)=C_2^{3}\begin{bmatrix} \frac{d pitch}{dt}\\ 0 \\ 0 \end{bmatrix} \end{aligned} \] >3. 分析和第二步类似。假设已经完成了第一组旋转，最后两组旋转没有完成，如果接着完成最后两组旋转，则绕ZZZ轴的角速度在两个坐标系下是一样的，则有如下公式： \[ \begin{aligned} \omega_b(yaw)=C_2^{3}C_1^{2}\begin{bmatrix} 0\\ 0 \\ \frac{d yaw}{dt} \end{bmatrix} \end{aligned} \]

  1. 通过对三次旋转的理解,可以得出,载体坐标系的三轴角速度\(\omega\)可以如下表示: \[ \begin{aligned} \omega_b&=\omega_b(yaw)+\omega_b(pitch)+\omega_b(roll) \\ &=C_2^{3}C_1^{2}\begin{bmatrix} 0\\ 0 \\ \frac{d yaw}{dt} \end{bmatrix}+C_2^{3}\begin{bmatrix} \frac{d pitch}{dt}\\ 0 \\ 0 \end{bmatrix}+\begin{bmatrix} 0\\ \frac{d roll}{dt} \\ 0 \end{bmatrix} \\ &=\begin{bmatrix} \cos \phi & 0 & -\sin \phi \cos \theta \\ 0 & 1 & 0 \\ \sin \phi & 0 & \cos \theta \cos \phi \end{bmatrix} \cdot \begin{bmatrix} \frac{d pitch}{dt} \\ \frac{d roll}{dt} \\ \frac{d yaw}{dt} \end{bmatrix} \\ &=\begin{bmatrix} \cos \phi & 0 & -\sin \phi \cos \theta \\ 0 & 1 & 0 \\ \sin \phi & 0 & \cos \theta \cos \phi \end{bmatrix} \cdot \frac{d \vartheta}{dt} \end{aligned} \]

  2. 于是,通过对矩阵求逆,可求出\(\frac{d \vartheta}{dt}\) \[ \begin{aligned} \frac{d \vartheta}{dt}= \begin{bmatrix} \frac{d pitch}{dt} \\ \frac{d roll}{dt} \\ \frac{d yaw}{dt} \end{bmatrix} = \begin{bmatrix} \cos \phi & 0 & \sin \phi \\ \sin \theta \sin \phi / \cos \theta & 1 & -\sin \theta \cos \phi / \cos \theta \\ -\sin \phi/ \cos \theta & 0 & \cos \phi /\cos \theta \end{bmatrix} \cdot \omega_b \end{aligned} \]

  3. 另外的,还可以参照第一讲的旋转矩阵R的导数\(\dot{R}=Rw_\times\),具体参照下面资料<方法二>

这部分参考资料: (1)<方法一:分步计算偏导:欧拉角微分方程推导> (2)<方法二:直接对旋转矩阵求偏导:欧拉角微分方程的推导>

1.6. IMU仿真