1. 线性方程组求解的直观感受
1.1. 非齐次线性方程组
求解下面的非齐次线性方程组 \[ \begin{cases} \text{ } 2x_{1}+3x_{2}+x_{3}=2 \\ \text{ } x_{1}-2x_{2}+2x_{3}=4 \\ \text{ } 3x_{1}+x_{2}+3x_{3}=6 \end{cases} \]
1.1.1. 第一步:列出增广矩阵
\[ \begin{pmatrix} 2& 3& 1& | 2 \\ 1& -2& 2&|4 \\ 3& 1& 3& |6 \\ \end{pmatrix} \]
1.1.2. 第二步:高斯消元,化成阶梯矩阵
1.1.2.1. 先把第2行换到第1行
\[ \begin{pmatrix} 1& -2& 2&|4 \\ 2& 3& 1& | 2 \\ 3& 1& 3& |6\\ \end{pmatrix} \] #### 1.1.2.2. 第2行减第1行的2倍,第3行减第1行的3倍,得到 \[ \begin{pmatrix} 1& -2& 2&|4 \\ 0& 7& -3& | -6 \\ 0& 7& -3& |-6\\ \end{pmatrix} \] #### 1.1.2.3. 第3行减第2行,得到 \[ \begin{pmatrix} 1& -2& 2&|4 \\ 0& 7& -3& | -6 \\ 0& 0& 0& |0\\ \end{pmatrix} \] #### 1.1.2.4. 化简后的方程组,等于 \[ \begin{cases} 2x_{1}+3x_{2}+x_{3}=2 \\ 7x_{2}-3x_{3}=6 \\ 0x_{1}+0x_{2}+0x_{3}=0 \\ \end{cases} \]
这样,\(x_2\)可以通过\(x_3\)来表示,\(x_1\)也可以通过\(x_3\)来表示,这样\(x_3\)就叫做自由变量,\(x_3\)可以取任意值。所以\(x_1\),\(x_2\),\(x_3\)就有无穷多个解。
对于非齐次线性方程组, 对线性方程组进行初等变换(高斯消元法),化为最简型(阶梯形)矩阵, 得到如下结论
- 考查系数矩阵r(A),增广矩阵r(A,b),以及方程组未知数个数n
- 如果系数矩阵的秩r(A)小于增广矩阵的秩r(A,b),r(A)<r(A,b),那么方程组无解
- 如果系统矩阵的秩小于方程组未知数个数但是等于増广矩阵的秩,r(A)=r(A,b)<n,那么方程组有多个解
- 如果系统矩阵的秩等于方程组未知数个数,r(A)=r(A,b)=n,那么方程组有唯一解
1.2. 齐次方程组
\[ \begin{cases} \text{ } 2x_{1}+3x_{2}+x_{3}=0 \\ \text{ } x_{1}-2x_{2}+2x_{3}=0 \\ \text{ } 3x_{1}+x_{2}+3x_{3}=0 \\ \end{cases} \]
齐次线性方程组,就是方程组的等式右边全部是0的方程组,只有系数矩阵,不需要增广矩阵,所以不会出现{0=d}形式的不相容方程。所以不会出现无解的情况,只需要考虑是多个解,还是唯一解。
对于齐次线性方程组, - 有多个解叫做有非零解。 - 唯一解叫做零解。
1.2.1. 判断零解
- 对于Ax=0的齐次线性方程组,列出其系数矩阵(不需要增广矩阵),使用高斯消元法化简,化为阶梯形矩阵,化简后,判断有效方程组个数(系数矩阵的秩)是否小于未知数个数
- 如果有效方程组个数小于未知数个数,叫做有非零解(多个解)
- 如果等于,叫做只有零解(唯一解)
- 直接判断系数矩阵的行列式 det A
- 判断detA,如果detA==0,则有非零解(无穷多个解)
- 判断detA,如果detA≠0,则只有零解(只有唯一解)
2. 线性方程组(更通用的定义)
2.1. 定义1: 线性方程组
\[ \begin{aligned} &a_{11}x_1 + a_{12}x_2 + \dots + a_{1n}x_n = b_1\\ &a_{21}x_1 + a_{22}x_2 + \dots + a_{2n}x_n = b_2\\ &\dots\\ &a_{m1}x_1 + a_{m2}x_2 + \dots + a_{mn}x_n = b_m\\ \end{aligned} \] 其中,矩阵 \[ \begin{aligned} A = \left( \begin{array}{ccc} a_{11} & \dots & a_{1n}\\ \vdots & \ddots & \vdots\\ a_{m1} &\dots & a_{mn}\\ \end{array} \right) \end{aligned} \] 称为该线性方程组的系数矩阵,而所有满足这个方程组的\(X = (x_1, \dots, x_n)^T\)的集合称为它的解集合
2.2. 定义2: 增广矩阵
上面线性方程组的系数矩阵如果加上右侧的\((b_1, b_2, \dots, b_n)^T\), 就构成了该方程组的增广矩阵
\[ \begin{aligned} A = \left( \begin{array}{ccc|c} a_{11} & \dots & a_{1n} & b_1\\ \vdots & \ddots & & \vdots\\ a_{m1} &\dots & a_{mn} & b_n\\ \end{array} \right) \end{aligned} \]
2.3. 高斯消去法
消元法是最常用的解线性方程组的方法,核心在于对增广矩阵进行初等变换(即数乘,倍加和对调) (具体案例见上面例子)
2.4. 线性方程组解的结构
2.4.1. 有无解的判定

2.4.2. 齐次方程组解的结构
- 对于齐次线性方程组,任意解的线性组合还是解
2.4.3. 定义: 基础解系 (只有齐次方程组才有)
齐次线性方程组的一组解向量\(\eta_1, \eta_2, \dots, \eta_t\), 如果满足两个条件: - (1) \(\eta_1, \eta_2, \dots, \eta_t\)线性无关 (即其中任意一个向量不能被剩余的其他向量线性组合表示) - (2)若该齐次线性方程组的任何一个解都能表示成\(\eta_1, \eta_2, \dots, \eta_t\)的线性组合,那么称\(\eta_1, \eta_2, \dots, \eta_t\)为该方程组的基础解系
齐次线性方程组基础解系的解向量个数: \[ n-r(A) \] 其中,\(n\)是方程组未知数个数,\(r(A)\)是系数矩阵的秩
基础解析解向量个数>=2, 若计算出来解向量只有1个的时候, 很有个可能这个方程组是非齐次线性方程组, 因为自由变量就有0和1两个选择, 至少会生成两个解向量
应用特性进行证明 题一 
题二 
2.4.4. 求基础解系步骤:
- 初等行变换, 将系数矩阵A化为阶梯型
- 得到的阶梯型系数矩阵的非零行数就是矩阵的秩序r(A)
- 把每个非零行最左端的非0系数对应的未知量\(x_i\)保留在等式左端, 其余\(n-r\)个未知量移到等式右端
- 再令右端的\(n-r\)个未知量的其中一个\(x_{(n-r),k}\)为1, 其余为0, 代入方程中计算出左侧未知量\(x_i\)
- 对步骤(4)进行\(n-r\)次操作, 就可以得到\(n-r\)个解向量\(\eta_j\), 这些解向量共同构成基础解系
- 基础解系可以写成\(k_1 \eta_1+ k_2 \eta_2 \cdots +k_{n-r}\eta_{n-r}\)
例子1 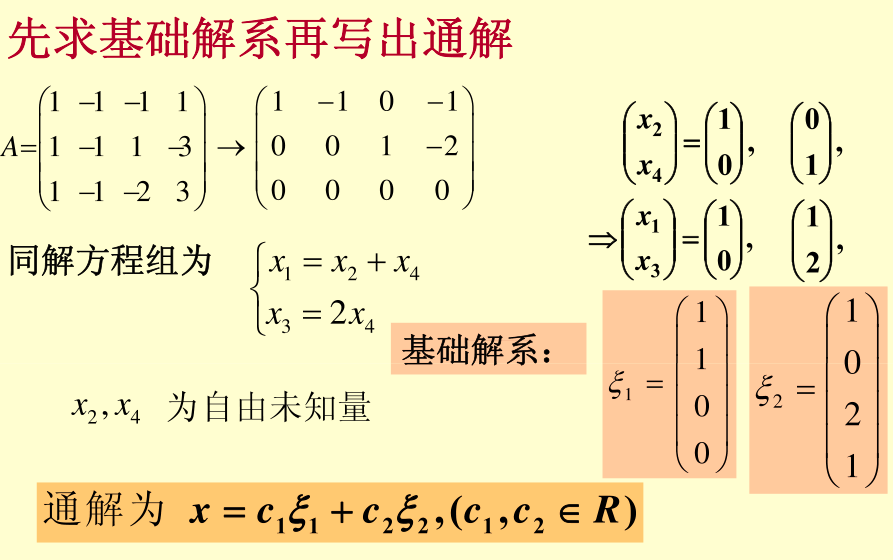
例子2 
例子3 
2.4.5. 非齐次线性方程组解的结构
假定有非齐次方程组: \[ \begin{aligned} &a_{11}x_1 + a_{12}x_2 + \dots + a_{1n}x_n = b_1\\ &a_{21}x_1 + a_{22}x_2 + \dots + a_{2n}x_n = b_2\\ &\dots\\ &a_{m1}x_1 + a_{m2}x_2 + \dots + a_{mn}x_n = b_m\\ \end{aligned} \]
其中,方程组右侧\(b_m\)不全为0
2.4.5.1. 定义: 导出组
把非齐次线性方程组的等式右侧全部为0, 变成齐次方程组, 该齐次方程组也称为这个非线性方程组的导出组
\[ \begin{aligned} &a_{11}x_1 + a_{12}x_2 + \dots + a_{1n}x_n = 0\\ &a_{21}x_1 + a_{22}x_2 + \dots + a_{2n}x_n = 0\\ &\dots\\ &a_{m1}x_1 + a_{m2}x_2 + \dots + a_{mn}x_n = 0\\ \end{aligned} \]
2.4.5.2. 特点
- 非齐次线性方程组任意两个解的差是它的导出组的解, 根据线性性质, 方程组右侧等于\([b-b]_{m \times 1}=[0]_{m \times 1}\), 对应齐次线性方程组
- 非齐次线性方程组的任意解与它的导出组的和还是该非齐次线性方程组的解(很好理解,基本同上面一致)
2.4.5.3. 定理:
假设\(\gamma_0\)是非齐次线性方程组的一个特解(符合方程条件的一个解就行),那么该非齐次线性方程组的任意一个解都可以表示成:
\[ \begin{aligned} \gamma = \gamma_0 + k_1 \eta_1 + k_2 \eta_2 + \dots + k_n \eta_n \end{aligned} \]
其中,\(k_1 \eta_1 + k_2 \eta_2 + \dots + k_n \eta_n\)是导出组基础解系的线性组合
根据定理, 可以得到非齐次线性方程组有唯一解的条件:即它的导出组只有零解, 对应的是r(A)满秩
参考: 1. 线性方程组解的分析:唯一解,无穷多解以及无解 2. 线性方程组什么时候无解?多个解?唯一解?