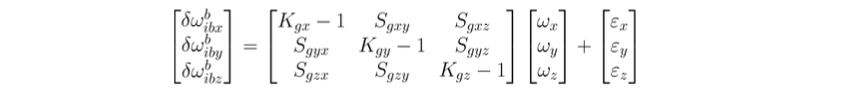捷联惯导更新算法
姿态更新算法
选取“东-北-天”地理坐标系作为惯导系统的导航参考坐标系,后面记为n系,则以n系作为参考系的姿态微分方程为:
\[ \dot{C}_b^n = C_b^n(\omega_{nb}^b \times) \]
其中,矩阵\(C_b^n\)表示载体坐标系(b系)相对于导航坐标系(n系)的姿态矩阵,由于陀螺仪输出的是b系相对于惯性系(i系)的角速度\(\omega_{ib}^b\),而角速度信息\(\omega_{nb}^b\)不能直接测量获得,因此,进一步分解,有:
\[ \begin{aligned} \dot{C}_b^n = C_b^n(\omega_{nb}^b \times)&= C_b^n[(\omega_{ib}^b-\omega_{in}^b)\times] \\ &= C_b^n(\omega_{ib}^b\times)-C_b^n(\omega_{in}^b\times) \\ &= C_b^n(\omega_{ib}^b\times)-C_b^n(\omega_{in}^b\times)C_b^bC_b^n \\ &= C_b^n(\omega_{ib}^b\times)-(\omega_{in}^n\times)C_b^n \end{aligned} \]
其中,
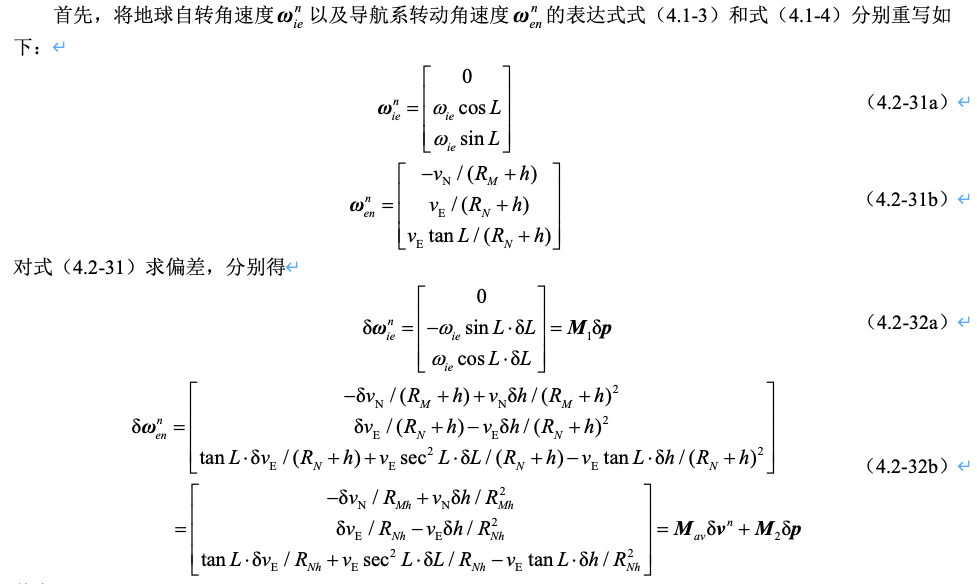
- \(\omega_{in}^n\)表示n系相对于i系的旋转,它包含两部分:地球自转引起的导航系旋转、以及惯导系统在地球表明附近运动因地球表面弯曲而引起的n系旋转,因此,有\(\omega_{in}^n=\omega_{ie}^n+\omega_{en}^n\)
\[ \omega_{ie}^n= \begin{bmatrix} 0 \\ \omega_{ie} \cos L \\ \omega_{ie} \sin L \end{bmatrix} \]
\[ \omega_{en}^n= \begin{bmatrix} -\frac{v_N}{R_M+h} \\ \frac{v_E}{R_N+h} \\ \frac{v_E}{R_N+h} \tan L \end{bmatrix} \]
其中,
- \(\omega_{ie}\)为地球自转角速率
- \(L\)表示地理纬度
- \(h\)表示高度
与矩阵微分方程\(\dot{C}_b^n = C_b^n(\omega_{nb}^b \times)\)相比,上面推导出来的离散化求解更麻烦,一般不会直接求解该方程,而是用如下方法解决姿态矩阵更新问题,
根据矩阵乘法,有:
\[ C_{b(m)}^{n(m)}=C_{i}^{n(m)}C_{b(m)}^{i} \]
其中,
- 角标符号m表示\(t_m\)时刻
- 由于i系是不动的惯性参考坐标系,其与时间无关,不需要标注时刻
由:
\[ C_{b(m)}^i=C_{b(m-1)}^iC_{b(m)}^{b(m-1)} \]
\[ C_{i}^{n(m)}=C_{n(m-1)}^{n(m)}C_{i}^{n(m-1)} \]
其中,
- 矩阵\(C_{b(m)}^{b(m-1)}\)表示以i系作为参考基准,b系从\(t_{m-1}\)时刻到\(t_{m}\)时刻的旋转变化,也就是以\(m-1\)时刻下的载体坐标系作为基准,\(t_m\)时刻下的载体姿态,同时也是载体从\(t_{m}\)时刻载体坐标系到\(t_{m-1}\)时刻载体坐标系的变换
- \(C_{b(m)}^{b(m-1)}\)可由陀螺仪角速度确定
- \(C_{n(m-1)}^{n(m)}\)表示以i系作为参考基准,n系从\(t_{m}\)时刻到\(t_{m-1}\)时刻的旋转变化
- \(C_{n(m-1)}^{n(m)}\)可以由计算角速度\(\omega_{in}^n\)确定
结合上面3条等式,有:
\[ \begin{aligned} C_{b(m)}^{n(m)}&=C_{i}^{n(m)}C_{b(m)}^{i} \\ &=C_{n(m-1)}^{n(m)}C_{i}^{n(m-1)} C_{b(m-1)}^iC_{b(m)}^{b(m-1)} \\ &=C_{n(m-1)}^{n(m)}C_{b(m-1)}^{n(m-1)}C_{b(m)}^{b(m-1)} \end{aligned} \]
其中,
- \(C_{b(m-1)}^{n(m-1)}\)表示\(t_{m-1}\)时刻的姿态阵
- \(C_{b(m)}^{n(m)}\)表示\(t_m\)时刻的姿态阵
若陀螺仪在时间段\([t_{m-1},t_m]\)内\((T=t_m-t_{m-1})\)进行了两次等间隔采样,角增量分别是\(\Delta \theta_{m1}\)和\(\Delta \theta_{m2}\),采用二子样圆锥误差补偿算法,有:
\[ C_{b(m)}^{b(m-1)}=M_{RV}(\phi_{ib(m)}^b)=\exp (\phi_{ib(m)}^b\times) \]
\[ \phi_{ib(m)}^b=(\Delta \theta_{m1}+\Delta \theta_{m2})+\frac{2}{3} \Delta \theta_{m1} \times \Delta \theta_{m2} \]
对于单子样,只需要把 \(\frac{2}{3}\) 改成 \(\frac{1}{12}\)
通常,在导航更新期间\([t_{m-1},t_m]\)内,可以认为由速度和位置引起的\(\omega_{in}^n\)变化很小,视为常数,记为\(\omega_{in(m)}^n\),则有:
\[ C_{n(m-1)}^{n(m)}=(C_{n(m)}^{n(m-1)})^T = [M_{RV}(\phi_{in(m)}^n)]^T \approx [M_{RV}(T*\omega_{in(m)}^n)]^T \]
速度更新算法
比力方程
比力方程是在地球表面附近进行惯性导航解算的基本方程
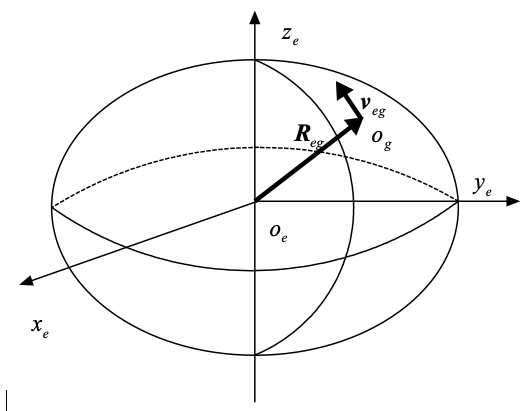
参见图,假设在地球表面附近有一运载体(惯导系统),其中心为\(o_g\)点,以\(o_g\)为原点定义当地地理坐标系(g系),\(o_g\)在地球坐标系(e系)下的矢径记为\(R_{eg}\) ,则\(R_{eg}\)在惯性坐标系(i系)和e系之间的投影变换关系为:
\[ R_{eg}^e = C_{i}^e R_{eg}^i \]
对上式两边同时微分,可得
\[ \dot{R}_{eg}^e =C_i^e \dot{R}_{eg}^i+\dot C_{i}^e R_{eg}^i = C_i^e \dot{R}_{eg}^i + [C_i^e (\omega_{ei}^i \times)]R_{eg}^i = C_{i}^e(\dot{R}_{eg}^i-\omega_{ie}^i \times R_{eg}^i) \]
其中,
- \(\dot{R}_{eg}^e\)表示g系原点\(o_g\)的速度,它是以e系作为参考坐标系的(即在e系观察得到的),即地速,\(v_{eg}^e=\dot{R}_{eg}^e\)
使用变换阵\(C_e^g\)同时对上式两边左乘:
\[ \begin{aligned} C_e^g v_{eg}^e &= C_e^g C_{i}^e(\dot{R}_{eg}^i-\omega_{ie}^i \times R_{eg}^i) \\ &= C_i^g (\dot{R}_{eg}^i-\omega_{ie}^i \times R_{eg}^i) \end{aligned} \]
其中,上式左侧的\(C_e^g v_{eg}^e\)表示地速在g系的投影,记为\(v_{eg}^g=C_e^g v_{eg}^e\)
所以,有:
\[ \begin{aligned} v_{eg}^g = C_i^g (\dot{R}_{eg}^i-\omega_{ie}^i \times R_{eg}^i) \end{aligned} \]
用\(C_{g}^i\)同时对上式两边左乘后,整理:
\[ C_{g}^i v_{eg}^g = (\dot{R}_{eg}^i-\omega_{ie}^i \times R_{eg}^i) \]
\[ \dot{R}_{eg}^i = C_{g}^i v_{eg}^g + \omega_{ie}^i \times R_{eg}^i \]
对上式两边同时微分,可得:
\[ \begin{aligned} \dot{v}_{eg}^g &= \dot{C}_{i}^g(\dot{R}_{eg}^i-\omega_{ie}^i \times R_{eg}^i) + C_i^g (\ddot{R}_{eg}^i - \omega_{ie}^i \times \dot{R}_{eg}^i) \\ &= \underbrace{C_i^g(\omega_{gi}^i \times)C_g^i v_{eg}^g}_{\dot{C}_{i}^g(\dot{R}_{eg}^i-\omega_{ie}^i \times R_{eg}^i)} + C_i^g[\ddot{R}_{eg}^i - \omega_{ie}^i \times (C_g^i v_{eg}^g + \omega_{ie}^i \times R_{eg}^i)] \\ &= C_i^g[\ddot{R}_{eg}^i-(\omega_{ie}^i \times)^2R_{eg}^i] + C_i^g[(\omega_{gi}^i-\omega_{ie}^i)\times]C_{g}^i v_{eg}^g \\ &= C_i^g[\ddot{R}_{eg}^i-(\omega_{ie}^i \times)^2R_{eg}^i] - (\omega_{ie}^g+ \omega_{ig}^g) \times v_{eg}^g \\ &= C_i^g[\ddot{R}_{eg}^i-(\omega_{ie}^i \times)^2R_{eg}^i] - (\omega_{ie}^g+ \omega_{ie}^g+ \omega_{eg}^g ) \times v_{eg}^g \\ &= C_i^g[\ddot{R}_{eg}^i-(\omega_{ie}^i \times)^2R_{eg}^i] - (2\omega_{ie}^g+ \omega_{eg}^g) \times v_{eg}^g \end{aligned} \]
由于\(R_{ig}^i=R_{ie}^i+R_{eg}^i\),当选择地心惯性系作为i系时,则i系和e系的坐标原点始终重合,即有\(R_{ie}^i=0\)和\(\ddot{R}_{eg}^i=\ddot{R}_{ig}^i\)
根据牛顿第二定律,有\(\ddot{R}_{ig}^i=f_{sf}^i+G^i\),其中:
- \(f_{sf}^i\)为比力
- \(G^i\)为地球引力加速度(注意,不是重力)
再根据地球重力公式\(g^i=G^i - (\omega_{ie}^i \times)^2 R_{eg}^i\)
可得:
\[ \begin{aligned} \dot{v}_{eg}^g &= C_i^g[\ddot{R}_{eg}^i-(\omega_{ie}^i \times)^2R_{eg}^i] - (2\omega_{ie}^g+ \omega_{eg}^g) \times v_{eg}^g \\ &= C_i^g(f_{sf}+g^i)-(2\omega_{ie}^g+ \omega_{eg}^g) \times v_{eg}^g \\ &= C_b^g f_{sf}^b - (2 \omega_{ie}^g+\omega_{eg}^g) \times v_{eg}^g +g^g \end{aligned} \]
将上式的地理过坐标系g系替换成“东-北-天”导航坐标系(n系),即可得到比力方程:
\[ \dot{v}_{en}^n = C_b^n f_{sf}^b - (2 \omega_{ie}^n + \omega_{en}^n )\times v_{en}^n + g^n \]
其中,
- \(f_{sf}^b\)为加速度的输出(比力)
- \((2 \omega_{ie}^n ) \times v_{en}^n\) 为由载体运动和地球自转引起的哥氏加速度
- \((\omega_{en}^n) \times v_{en}^n\)为载体运动引起的对地向心加速度
- \(g^n\)为重力加速度
- \(- (2 \omega_{ie}^n + \omega_{en}^n )\times v_{en}^n + g^n\)统称为有害加速度
- 以东北天坐标系为导航坐标系,则\(g^n=[0,0,-9.81]\)
比力方程表明,加速度计输出中扣除有害加速度后,才能获取载体再导航坐标系的几何运动加速度\(\dot{v}_{en}^n\)
有时,为了计算简便,会把哥氏加速度和向心加速度忽略,即\(\dot{v}_{en}^n = C_b^n f_{sf}^b + g^n\)
综上,可得,速度更新方程:
\[ \begin{aligned} V_{m}=V_{m-1}+[\dot{v}_{en}^n]\Delta T \end{aligned} \]
或者由简化形式:
\[ \begin{aligned} V_{m}=V_{m-1}+\frac{1}{2}( C_{b(m-1)}^{n(m-1)}f_{sf(m-1)}^b + C_{b(m)}^{n(m)}f_{sf(m)}^b )\Delta T \end{aligned} \]
位置更新算法
由位置微分方程:
\[ \dot{P} = V \]
可得,位置更新方程:
\[ \begin{aligned} P_{m}=P_{m-1}+\frac{1}{2}(V_m+V_{m-1})\Delta T \end{aligned} \]
捷联惯导误差分析
基本方法——误差分析的思路
误差方程的形式——需要求的是啥?
假设给定微分方程:
\[ \begin{aligned} \dot{z}=x+y \end{aligned} \]
且:
\[ \begin{aligned} \tilde{z}&=z+\delta z \\ \tilde{x}&=x+\delta x \\ \tilde{y}&=y+\delta y \end{aligned} \]
则误差方程的形式为:
\[ \begin{aligned} \delta \dot{z}= ??? \end{aligned} \]
- 写出原微分方程
\[ \begin{aligned} \dot{z}=x+y \end{aligned} \tag{1} \]
写出考虑误差时的微分方程
即把\(\dot{z}=x+y\)使用带有误差的变量代替,得到:
\[ \begin{aligned} \tilde{\dot{z}}=\tilde{x}+\tilde{y} \end{aligned} \tag{2} \]
求出误差关系(真实值与理想值的关系)
这一步中,并非所有的关系都是已知的,有些需要自己推
\[ \begin{aligned} \tilde{z}&=z+\delta z \\ \tilde{x}&=x+\delta x \\ \tilde{y}&=y+\delta y \end{aligned} \tag{3} \]
- 把(3)的误差关系代入到等式(2)
\[ \begin{aligned} \dot{z}+\delta{\dot{z}}=x+\delta x+ y+ \delta y \end{aligned} \tag{4} \]
- 取原微分方程(1),代入(4)
\[ \begin{aligned} \because \dot{z}&=x+y \\ \therefore x+y + \delta \dot{z}&=x + y+ \delta x+\delta y \end{aligned} \tag{5} \]
- 化简
\[ \delta \dot{z} =\delta x+ \delta y \]
姿态误差方程
写出原微分方程
以“东-北-天(E-N-U)”坐标系为导航坐标系(n系),“右-前-上”坐标系为(b系)时,姿态微分方程可以表示为
\[ \dot{C}_b^n = C_b^n(\omega_{nb}^b \times) \]
当考虑地球自转角速度时,不易直接测量,因此上面的微分方程可以拆解为:
\[ \begin{aligned} \dot{C}_b^n = C_b^n(\omega_{nb}^b \times)&= C_b^n[(\omega_{ib}^b-\omega_{in}^b)\times] \\ &= C_b^n(\omega_{ib}^b\times)-C_b^n(\omega_{in}^b\times) \\ &= C_b^n(\omega_{ib}^b\times)-C_b^n(\omega_{in}^b\times)C_b^bC_b^n \\ &= C_b^n(\omega_{ib}^b\times)-(\omega_{in}^n\times)C_b^n \end{aligned} \tag{1} \]
其中,\(\omega_{in}^n\)表示导航系(n系)相对于惯性系(i系)的旋转,它包含地球自转和导航系相对于地球的旋转,其表达式为:
\[ \omega_{in}^n = \omega_{ie}^n + \omega_{en}^n \]
- 写出考虑误差的微分方程:
\[ \begin{aligned} \dot{\tilde{C}_b^n}= \tilde{C}_b^n( \tilde{\omega}_{ib}^b\times)-( \tilde{\omega}_{in}^n\times) \tilde{C}_b^n \end{aligned} \tag{2} \]
- 求出误差关系(真实值与理想值的关系)
- 姿态误差关系
- imu角速度误差关系
- 导航系计算误差关系
姿态误差关系
理想情况下,从载体坐标系(b系)到导航坐标系(n系)的变换矩阵为\(C_b^n\),而姿态计算时会有误差,一般假设误差在n系(global)上。
有误差的导航坐标系称为计算导航坐标系,简记为\(n'\)系。此时有误差的姿态矩阵\(\tilde{C}_b^n\)表示为
\[ \tilde{C}_b^n = C_b^{n'}=C_n^{n'}C_b^n \]
以n系作为参考坐标系,记从 n' 系到 n 系的旋转矩阵为\(C_\phi\),n'系在n系中的姿态为\(C_\phi\),对应的等效旋转矢量为\(\phi\)(其3个元素也被称作失准角),也就是说,n系绕等效旋转矢量为\(\phi\)旋转之后,得到n' 系
当\(\phi\)为小量时,根据等效旋转矢量与方向余弦阵关系式——罗德里格斯公式:
\[ C_{n'}^{n}=I+\frac{\sin \phi}{\phi}(\phi \times)+ \frac{1-\cos \phi}{ \phi^2}(\phi \times)^2 \approx I+(\phi \times) \]
\[ C_n^{n'}=I-\frac{\sin \phi}{\phi}(\phi \times)+ \frac{1-\cos \phi}{ \phi^2}(\phi \times)^2 \approx I-(\phi \times) \]
这个怎么理解,假设n系矩阵\(C_n\)等于\(I\), 对n系绕z轴逆时针旋转\(30\)度,得到n'系,这个等效旋转矢量是\(\phi=[0,0,\frac{1}{6} \pi]\),那么n'系在n系的姿态是\(I+(\phi \times)\),n'系到n系的旋转变换为\(C_{n'}^{n}=I+(\phi \times)\)
因此,带误差的姿态矩阵表示为:
\[ \begin{aligned} \tilde{C}_b^{n}=C_b^{n'} = C_n^{n'}C_b^n = [I-(\phi \times)] C_b^n \end{aligned} \tag{3} \]
IMU角速度误差关系
陀螺仪测量误差关系:
\[ \tilde{\omega}_{ib}^b = \omega_{ib}^b + \delta \omega_{ib}^b \]
一般来说,imu内参的影响会在imu测量的时候先补偿掉,这里就不用考虑了
导航系计算误差
\[ \tilde{\omega}_{in}^n=\tilde{\omega}_{ie}^n+\tilde{\omega}_{en}^n = \omega_{ie}^n + \delta \omega_{ie}^n + \omega_{en}^n + \delta \omega_{en}^n \]
在实际使用过程中,对于mems惯导,可以忽略这误差:
- 在中等精度及以下的惯性导航中,这两项角速度误差相比于器件误差,量级太小,没有考虑的必要;
- 在组合导航中,速度误差和位置误差一直被修正,会使他们的量级进一步减小。
两项误差的具体推导如下:
- 将(3)中的误差关系代入(2)
- 姿态误差关系: \(\tilde{C}_b^{n} = [I-(\phi \times)] C_b^n\)
- imu测量误差关系: \(\tilde{\omega}_{ib}^b = \omega_{ib}^b + \delta \omega_{ib}^b\)
- 导航系计算误差关系: \(\tilde{\omega}_{in}^n= \omega_{ie}^n + \delta \omega_{ie}^n + \omega_{en}^n + \delta \omega_{en}^n\)
对式(2)重新抄写如下:
\[ \begin{aligned} \dot{\tilde{C}_b^n}= \tilde{C}_b^n( \tilde{\omega}_{ib}^b\times)-( \tilde{\omega}_{in}^n\times) \tilde{C}_b^n \end{aligned} \tag{2} \]
代入之后,可得:
\[ \begin{aligned} (-\dot{\phi}\times)C_{b}^n +[I-(\phi\times)]\dot{C}_n^b = [I-(\phi \times)]C_b^n[(\omega_{ib}^b+\delta \omega_{ib}^b)\times]-(\omega_{in}^n\times)[I-(\phi \times)]C_b^n \end{aligned} \tag{4} \]
- 将(1)中的原微分方程代入(4)
\[ \begin{aligned} (-\dot{\phi}\times)C_b^n + [I - (\phi \times)][C_b^n (\omega_{ib}^b\times)-(\omega_{in}^n)C_b^n] \\ = [I-(\phi \times)]C_b^n[(\omega_{ib}^b+\delta \omega_{ib}^b)\times]-(\omega_{in}^n\times)[I-(\phi \times)]C_b^n \end{aligned} \]
- 化简
- 两边同时右乘\(C_n^b\)
- 展开,忽略其中的二阶项
- 利用定理\((a\times)(b\times)-(b\times)(a\times)=[(a\times b)\times]\) 进一步化简
最终,得到:
\[ (\dot{\phi}\times)=[(\phi \times \omega_{in}^n -\delta \omega_{ib}^n)\times] \]
最后,把两边的反对称符号同时去掉
\[ \dot{\phi} = \phi \times \omega_{in}^n - \delta \omega_{ib}^n \]
速度误差方程
- 写出原微分方程
\[ \begin{aligned} \dot{V}^n=C_b^n f^b + g^n \end{aligned} \tag{1} \]
- 写出考虑误差的微分方程
\[ \begin{aligned} \dot{\tilde{V}}^n = \tilde{C}_b^n \tilde{f}^b + \tilde{g}^n \end{aligned} \tag{2} \]
- 求出误差关系(真实值与理想值的关系)
\[ \begin{aligned} & \tilde{V}^n = V^n +\delta V^n \\ & \tilde{C}_b^n = [I-\phi\times]C_b^n \\ & \tilde{f}^b = f^b +\delta f^b \\ & \tilde{g}^n = g^n +\delta g^n \end{aligned} \tag{3} \]
其中:
- \(\delta f^b\)表示加速度测量误差
- \(g^n\)表示重力误差,非高精度模型下可忽略
- 将(3)代入(2)
\[ \begin{aligned} \dot{V}^n+\delta \dot{V}^n = (I-\phi \times)C_b^n(f^b+\delta f^b)+g^n \end{aligned} \tag{4} \]
- 将原微分方程代入(4)
\[ \begin{aligned} C_b^n f^b +g^n + \delta \dot{V}^n = (I-\phi \times)C_b^n(f^b+\delta f^b)+g^n \end{aligned} \tag{5} \]
- 化简
\[ \begin{aligned} \delta \dot{V}^n &= C_b^n \delta f^b - (\phi \times)C_b^n(f^b +\delta f^b) \\ & \approx C_b^n \delta f^b - (\phi \times)C_b^n(f^b) \\ &= \delta f^n + (f^n \times)(\phi) \end{aligned} \tag{6} \]
位置误差方程
- 写出原微分方程
\[ \begin{aligned} \dot {P} = V \end{aligned} \tag{1} \]
- 写出考虑误差的微分方程
\[ \begin{aligned} \dot{\tilde{P}}=\tilde{V} \end{aligned} \tag{2} \]
- 求出误差关系(真实值与理想值的关系)
\[ \begin{aligned} \tilde{P} = P + \delta P \\ \tilde{V} = V + \delta V \end{aligned} \tag{3} \]
- 将(3)代入(2)
\[ \begin{aligned} \dot{P} + \delta \dot{P} = V+ \delta V \end{aligned} \]
- 将原微分方程代入(4)
\[ \begin{aligned} V+\delta \dot{P} = V+ \delta V \end{aligned} \tag{5} \]
- 化简
\[ \begin{aligned} \delta \dot{P} = \delta V \end{aligned} \tag{6} \]
整理
姿态误差方程
\[ \begin{aligned} \dot{\phi} = \phi \times \omega_{in}^n - \delta \omega_{ib}^n \end{aligned} \]
速度误差方程
\[ \begin{aligned} \delta \dot{V}^n = \delta f^n + (f^n \times)(\phi) \end{aligned} \]
位置误差方程
\[ \begin{aligned} \delta \dot{P} = \delta V \end{aligned} \]