On the Covariance of ICP-based Scan-matching Techniques

摘要
本文研究迭代最近点(ICP)算法计算旋转平移的协方差估计问题。这个问题与移动机器人和装备了深度传感相机(如Kinect)或激光雷达(如Velodyne)的车辆的定位问题有关。以往文献中提出的封闭形式的协方差公式通常建立在ICP的解是通过最小化线性最小二乘问题得到的这一事实之上。在本文中,我们表明这种方法需要谨慎,因为算法的重新匹配步骤没有显式解释,并将其应用于点到点版本的ICP导致完全错误的协方差。然后,我们给出了一个形式化的数学证明,证明了该方法在点到平面的ICP版本中是有效的,从而验证了从业者的直觉和实验结果。
介绍
相对旋转-平移估计的协方差不仅取决于传感器噪声特性,还取决于环境的几何形状。实际上,当使用ICP进行扫描匹配时,有几个误差来源会起作用:
- 在一次扫描中没有在后续扫描中观察到几何图形的存在,也就是说,缺乏重叠
- 点的不匹配,也就是说,如果扫描开始时彼此距离很远,则ICP可能会降到局部(而不是全局)最小值,从而产生错误的旋转平移估计
- 即使1)和2)没有发生,由于传感器噪声和可能的欠约束环境(如长而无特征的走廊),计算出的估计仍然具有不确定性
在实践中,第一个问题可以通过拒绝具有过多距离度量或位于扫描边界[11]附近的点对来解决,第二个问题可以通过使用航迹估计预对齐扫描或使用足够快的采样率来解决。因此,我们将把重点放在第三个误差来源上。
通过扫描匹配算法(如ICP)得到的估计的协方差可以从文献[12],[13]得到。
要估计的变换\(\hat{x}\)由代价函数J(x, z)的局部argmin得到,其中\(z\)为当前扫描到的点云。
结果,我们期望得到\(\frac{\partial}{\partial x} J(\hat{x}, z)=0\),根据隐函数定理,此时x是数据z在这个函数最小值附近。
因此,如果此时观测数据z(点云)有一个小的扰动\(\delta z\),意味着\(\delta x\)也有小的变化\(\frac{\partial^2 J}{\partial x^2} \delta x+\frac{\partial^2 J}{\partial z \partial x} \delta z=0\),即有:
\[ \delta x=-\left(\frac{\partial^2 J}{\partial x^2}\right)^{-1} \frac{\partial^2 J}{\partial z \partial x} \delta z \]
因此,如果\(\delta z\)表示由于传感器噪声造成的测量(随机)差异,则估计中相应的可变性\(\delta x=\hat{x}-x\),其中方差为:
\[ \mathbb{E}\left(\delta x \delta x^T\right)=\operatorname{cov}(\hat{x}) \]
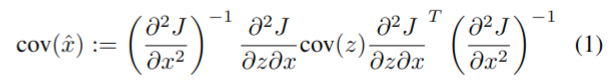
我们的目标是指出这个公式在ICP协方差计算方面的潜在有效性不足,但也要描述它可以安全使用的情况。具体来说,几何配准(1)的问题在于它依赖于\(\delta x=-\left(\frac{\partial^2 J}{\partial x^2}\right)^{-1} \frac{\partial^2 J}{\partial z \partial x} \delta z\),这是基于局部隐函数定理的,它只适用于无穷小的变化\(\delta x, \delta z\)。在ICP的情况下,无穷小意味着亚像素位移,的确,在匹配扫描时,ICP执行的重新匹配步骤使代价函数远不是平滑的,因此对代价函数进行泰勒展开有:
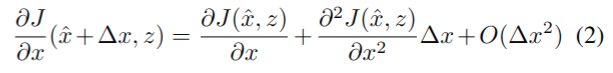
这在极限∆x→0中是正确的,但当位移∆x大于几个像素时,结果可能完全错误。这方面的一个例子将在Section II-A.2. 中给出。另一方面,如果将配准误差投影到参考曲面上,如点到面ICP[2],则式(1)将给出有效结果。这将在第三节中得到正式证明。
我们的论文是[13]和[14]结果的推广和严格证明。我们的主要贡献是指出盲目应用(1)的潜在缺点。然后基于第三节中的几何论证,为(1)点到面ICP的有效性提供形式化的数学证明。最后,我们将在第四节中用一个简单的3D示例说明结果。