1. 线性系统的近似线性化
严格来说,大多物理系统都是非线性的,难以求解,即 \[ \left \{ \begin{aligned} \dot{x}=f(x,u) \\ y=g(x,u) \end{aligned} \right. \] 在误差允许范围内,可以使用线性系统来近似,有:
- 确定线性化点

- 对非线性函数在线性化点处进行泰勒展开,有:
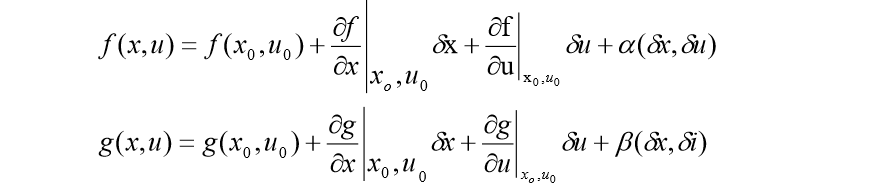
其中,两式的最后一项\(\alpha\)和\(\beta\)是关于\((\delta x,\delta u)\)的高次项,在这里暂时忽略
并且引入了下面的符号:
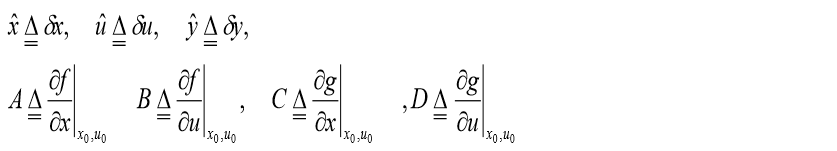
- 求解线性化处的雅可比
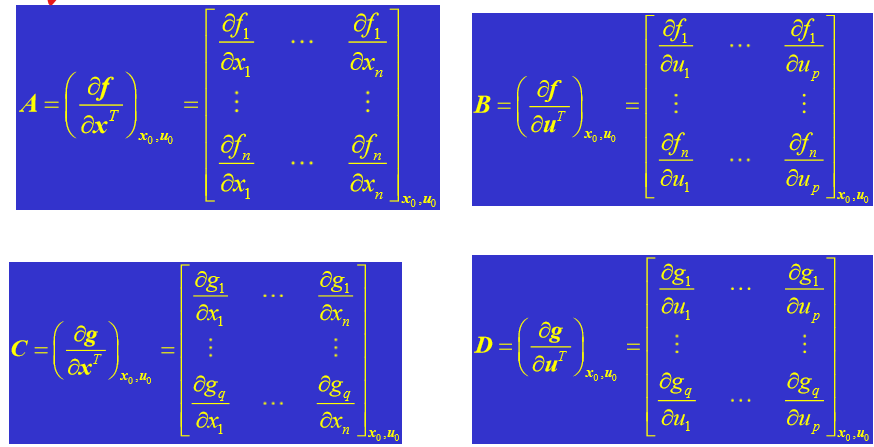
- 线性化后的状态空间表达式为 \[ \dot{\hat{x}}=A\hat{x}+B\hat{u} \]
\[ \hat{y}=C\hat{x}+D\hat{u} \]
1.1. 例子1
对下面的系统在\(x_0=0\)处线性化
\[ \left \{ \begin{aligned} \dot{x}_1 &= x_2 \\ \dot{x}_2 &=x_1+x_2+x_2^3+2u \\ y &=x_1+x_2^2 \end{aligned} \right . \]
由系统状态方程,有
\[ \left \{ \begin{aligned} f_1 &= x_2 \\ f_2 &=x_1+x_2+x_2^3+2u \\ g &=x_1+x_2^2 \end{aligned} \right . \]
根据下面的雅克比求解规则,有:

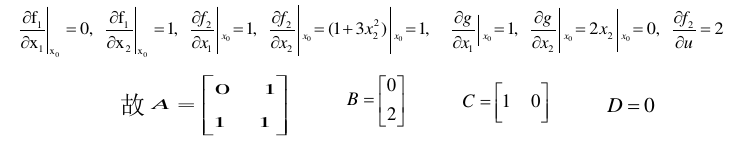
1.2. 例子2
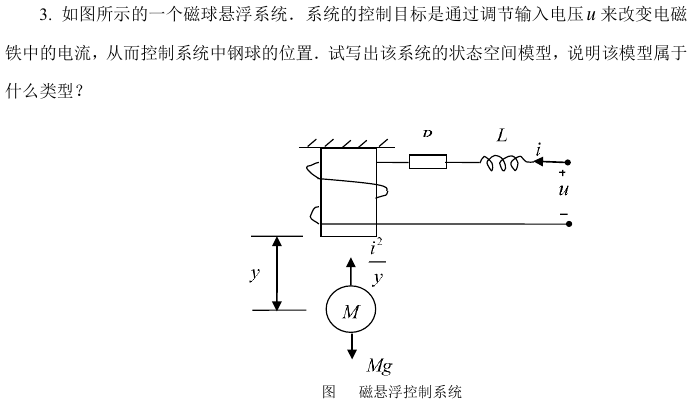
解:
- 写出微分方程有:
\[ \begin{aligned} L\frac{d i}{d t} + iR = u \\ M\frac{d y^2}{d^2t} = Mg-\frac{i^2}{y} \end{aligned} \]
- 对微分方程进行拉氏变换
\[ \left \{ \begin{aligned} s L I(s) + I(s) R = U(s) \\ s^2 M Y(s) = Mg -\frac{I^2(s)}{Y(s)} \end{aligned} \right . \]
- 选取状态变量
\[ \begin{aligned} x= \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} i \\ y \\ \frac{d y}{d t} \end{bmatrix} \end{aligned} \]
- 写出状态方程
\[ \left \{ \begin{aligned} sI(s) = -\frac{R}{L}I(s)+U(s) &\longleftrightarrow \dot{x}_1=\dot{i} = -\frac{R}{L} i + u = -\frac{R}{L} x_1 + u\\ &\longleftrightarrow \dot{x}_2=\dot{y}=\frac{dy}{dt}=x_3 \\ s^2 Y(s) = g -\frac{I^2(s)}{MY(s)} &\longleftrightarrow \dot{x}_3=\dot{\frac{dy}{dt}}=\frac{dy^2}{d^2t}=g -\frac{i^2}{My} = g -\frac{x_1^2}{Mx_2} \end{aligned} \right . \]
- 在\(x_0\)处进行线性化
注意到\(\dot{x}_3\)状态方程是非线性的,因此需要进行线性化
将系统在平衡点\(y_0=x_{20}=\)常数 处进行线性化,于是,进一步推出:
\[ \dot{x}_{20}=\frac{dy}{dt} |_{y=y_0}=x_{30}=0 \]
\[ \dot{x}_{30}=\dot{\frac{dy}{dt}}=\frac{dy^2}{d^2t}|_{y=y_0}=0 \]
将上式代入等式:
\[ M\frac{d y^2}{d^2t} = Mg-\frac{i^2}{y} \]
可得\(x_{10}=i_0=\sqrt{Mgx_{20}}\)
- 求\(\dot{x}_3\)状态方程\(f_3\)的雅克比\(j_3\)
\[ \frac{d f_3}{ d x^T}= \begin{bmatrix} -\frac{2 i_0}{M y_0} & \frac{i_0^2}{y_0^2} & 0 \end{bmatrix} \]
- 写出矩阵A,B
\[ \begin{aligned} A= \begin{bmatrix} -\frac{R}{L} & 0 & 0 \\ 0 & 0 & 1 \\ -\frac{2 i_0}{M y_0} & \frac{i_0^2}{y_0^2} & 0 \end{bmatrix} = \begin{bmatrix} -\frac{R}{L} & 0 & 0 \\ 0 & 0 & 1 \\ -2\sqrt{\frac{g}{M x_{10}}} & \frac{g}{x_{10}} & 0 \end{bmatrix} \end{aligned} \]
\[ \begin{aligned} B= \begin{bmatrix} \frac{1}{L} \\ 0 \\ 0 \end{bmatrix} \end{aligned} \]
- 最后有:
\[ \Delta \dot{x}=A\Delta x + B\Delta u \]
其中,\(\Delta x= x-x_0\)