Adjoints
我们将介绍李群伴随的概念,这将帮助我们将右边的增量或矫正值与左边的增量或校正值联系起来。这种性质使我们能够用代数方法处理李群定义的不确定性,并得到不同协方差变换的表达式。我们将重点讨论3D构造,即 SE (3),因为它的广泛适用性,但类似的定义应该适用于其他李群,因为他们主要依赖于伴随的定义。
Barfoot 和 Furgale (2014年)和 Mangelson 等人(2020年)的文献中已经出现了大多数这样的表达式,但由于它们遵循左手惯例,所以不能直接用于 GTSAM。我们为 Mangelson 等人之后的协方差变换提供了结果表达式,但是我们建议参考他们的工作来理解这个过程的细节。
让我们考虑一个例子,我们在一个姿态\(\mathbf{T}_{WB_i}\)加入小增量\(_{B_i}\mathbf{\xi}\):
\[ \begin{aligned} \mathbf{T}_{W_i B_{i}} \text{Exp}( _{B_i}\mathbf{\xi}) \end{aligned} \]
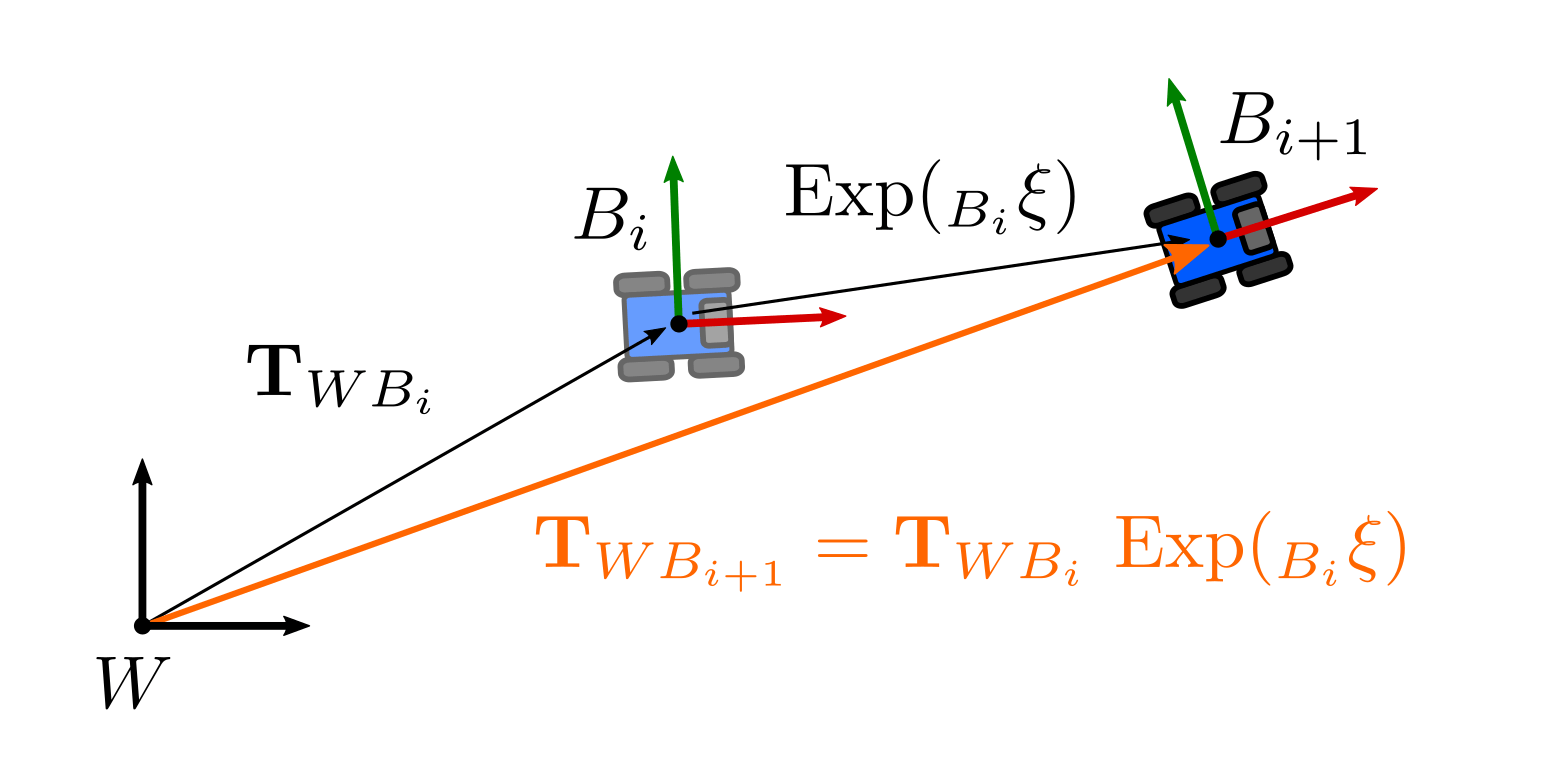
以上遵循了right-hand定则,与GTSAM一致
然而,一些应用则使用left-hand的形式:
\[ \begin{aligned} \mathbf{T}_{W_{i+1} B} = \text{Exp}( _{W_i}\mathbf{\xi}) \mathbf{T}_{W_i B_i} \end{aligned} \]
那么,对应的就是参考坐标系的增量变化:
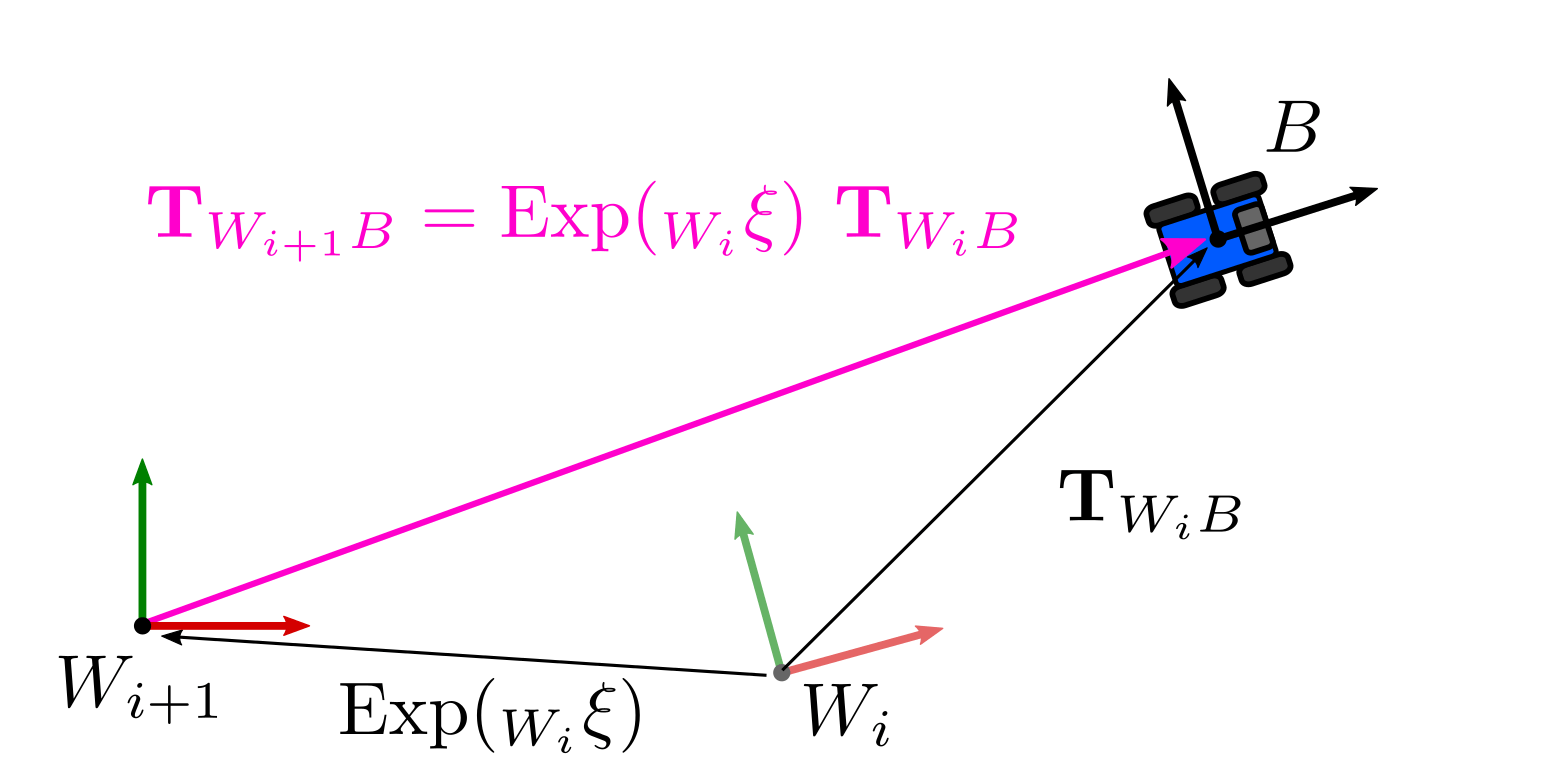
实际上,两种表达的意义都是一样的:

即有如下等式(暂时忽略时间索引):
\[ \begin{aligned} \text{Exp}( _{W}\mathbf{\xi}) \mathbf{T}_{WB} = \mathbf{T}_{WB} \text{Exp}( _{B}\mathbf{\xi}) \end{aligned} \]
进一步的,就可以根据body系的增量来求出world系的增量:
\[ \begin{aligned} \text{Exp}( _{W}\mathbf{\xi}) = \mathbf{T}_{WB} \text{Exp}( _{B}\mathbf{\xi}) \mathbf{T}_{WB}^{-1} \end{aligned} \]
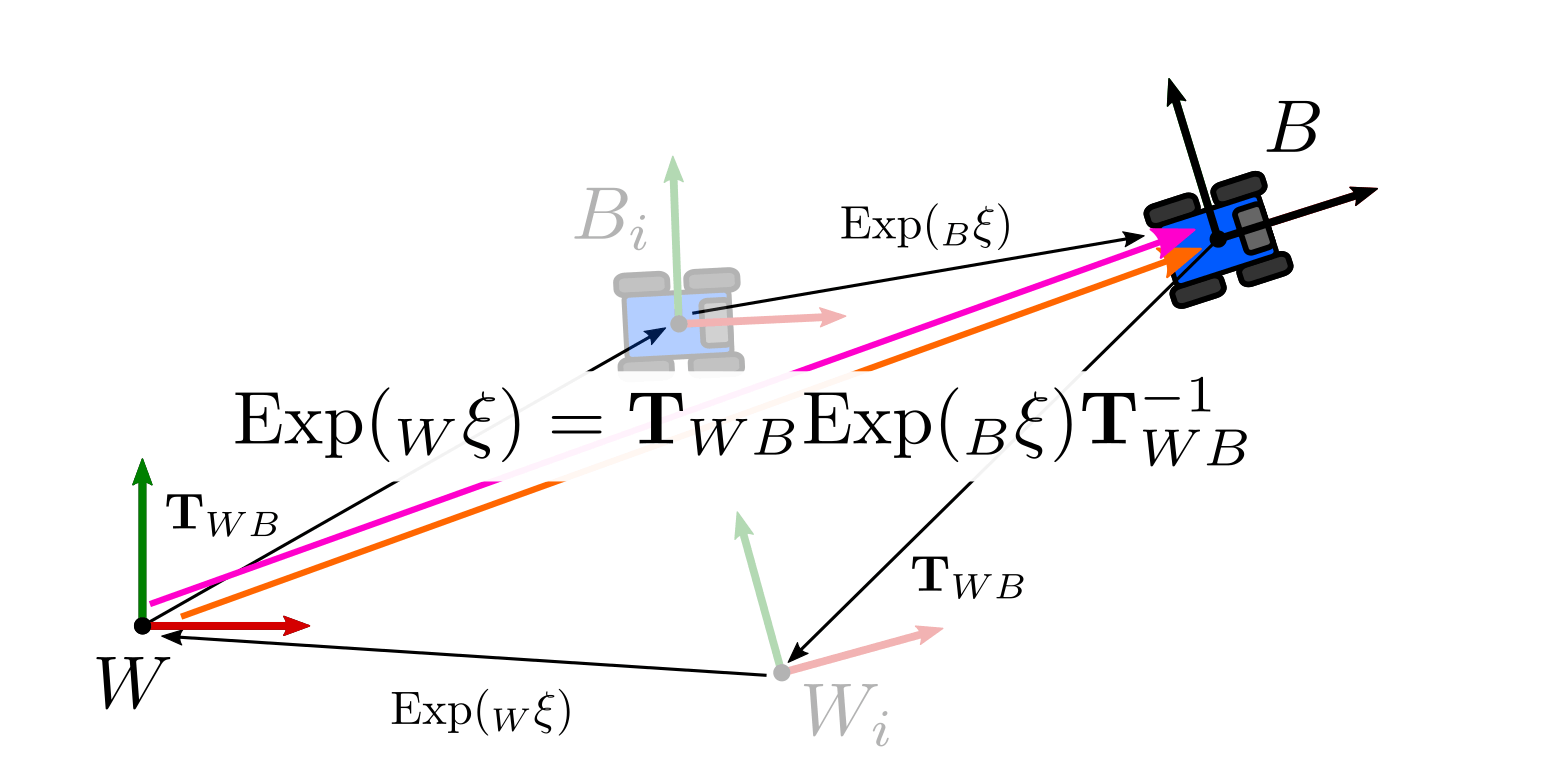
对于我们的目的,使用一个等价的替代表达式是有用的,它直接应用于切空间的元素(solà等人给出了一个更完整的推导,由于一些属性我们在这里省略了) :
\[ \begin{aligned} \text{Exp}( _{W}\mathbf{\xi}) \mathbf{T}_{WB_i} = \mathbf{T}_{WB_i} \text{Exp}( \text{Ad}_{T_{WB_i}^{-1}} {_{W}}\mathbf{\xi}) \end{aligned} \]
其中,\(\text{Ad}_{T_{WB_i}^{-1}}\)称为\(T_{WB_i}^{-1}\)的伴随,伴随直接作用于切线空间的元素上,改变它们的参考坐标系,即:
\[ {_{B}}\mathbf{\xi} = \text{Ad}_{T_{WB_i}^{-1}} {_{W}}\mathbf{\xi} \]
我们也可以把这解释为一种方法,将左边(在世界坐标系中)施加的增量一致地移动到右边(body坐标系) ,这对于保持右边惯例对于回溯和概率分布的一致性特别有用。
这是我们用来定义一些协方差转换的主要属性,并且它已经在
GTSAM的Pose3中实现为AdjointMap。
Distribution of the inverse
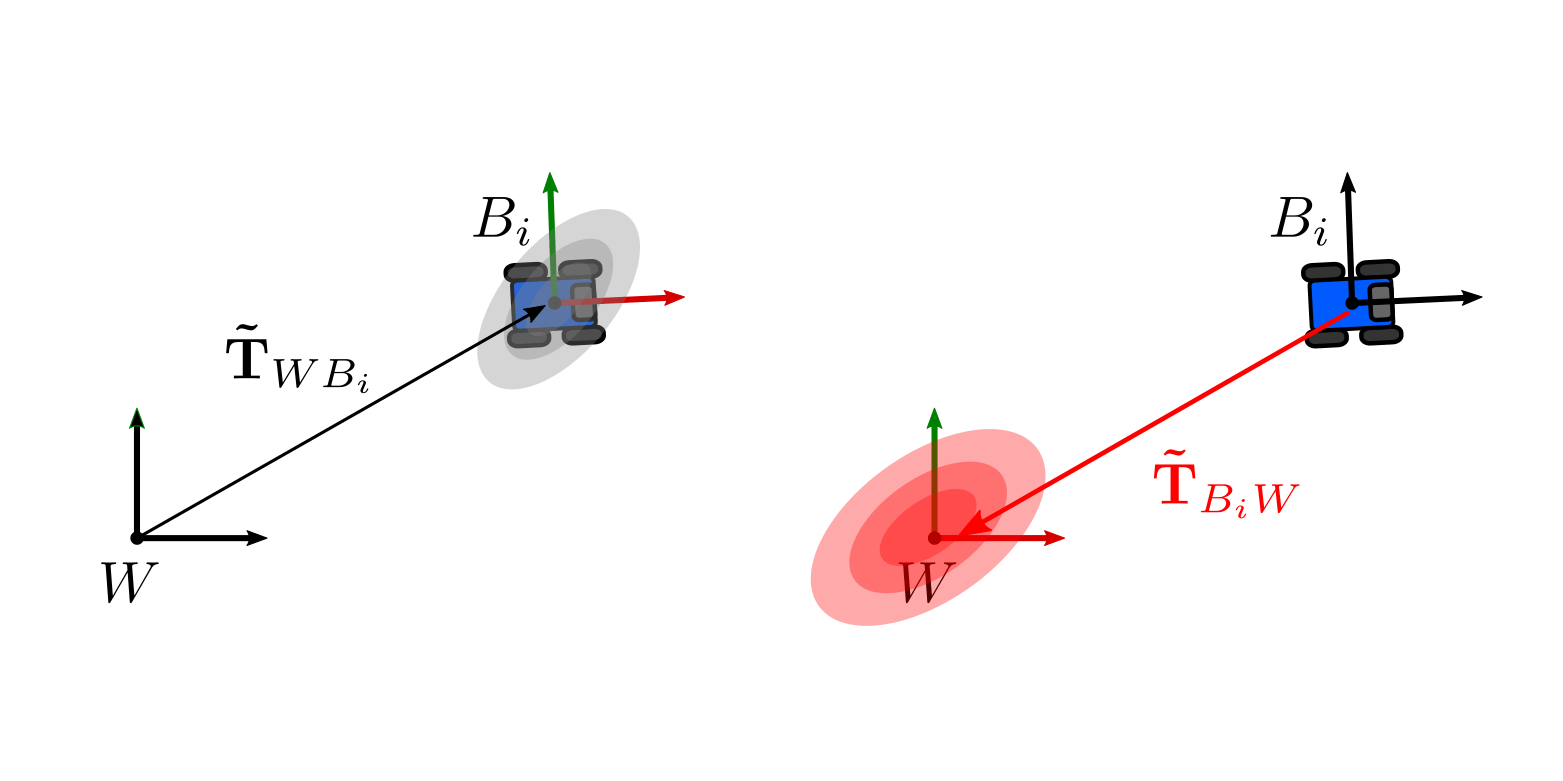
考虑这样一种情况: 我们有一个因子图的解,其协方差定义在body坐标系中。我们感兴趣的是获得一个表示world坐标系的协方差表达式.
 |
|---|
| 给定body坐标系的协方差\(B_i\)(左图),然而我们感兴趣的是右图的世界坐标系的协方差\(W\) |
假设具有正态分布的位姿表达如下:
\[ \begin{aligned} \mathbf{\tilde{T}}_{WB} = \mathbf{T}_{WB} \text{Exp}( _{B}\mathbf{\eta}) \end{aligned} \]
其中,\(_{B}\mathbf{\eta}\)是协方差为\(\Sigma_{B}\)的零均值高斯分布噪声,因此,逆位姿的分布可以通过对位姿表达式求逆:
\[ \begin{aligned} (\mathbf{\tilde{T}}_{WB})^{-1} & = (\mathbf{T}_{WB} \text{Exp}( _{B}\mathbf{\eta}) )^{-1}\\ & = (\text{Exp}( _{B}\mathbf{\eta}) )^{-1}\ \mathbf{T}_{WB}^{-1}\\ & = \text{Exp}(- _{B}\mathbf{\eta}) \ \mathbf{T}_{WB}^{-1} \end{aligned} \]
然而,在求逆后,噪声项被定义在左边,并且仍然是body坐标系下的表达,接下来使用伴随来将这一项移到右边:
1.根据前面推导的:
\[ \begin{aligned} \text{Exp}( _{W}\mathbf{\xi}) \mathbf{T}_{WB_i} = \mathbf{T}_{WB_i} \text{Exp}( \text{Ad}_{T_{WB_i}^{-1}} {_{W}}\mathbf{\xi}) \end{aligned} \]
2.应用于位姿的逆表达(等号右侧),则有:
\[ \begin{aligned} \text{Exp}( -{_{B}}\mathbf{\eta}) \mathbf{T}_{WB}^{-1} = \mathbf{T}_{WB}^{-1} \text{Exp}( -\text{Ad}_{T_{WB}} {_{B}}\mathbf{\eta}) \end{aligned} \]
3.因此,有:
\[ \begin{aligned} (\mathbf{\tilde{T}}_{WB})^{-1} = \ \mathbf{T}_{WB}^{-1}\ \text{Exp}(- \text{Ad}_{\mathbf{T}_{WB}} {_{B}}\mathbf{\eta}) \end{aligned} \]
最终,得到了符合right-hand的分布,其中定义了world坐标系的协方差,如下:
\[ \begin{aligned} \Sigma_{W} = \text{Ad}_{\mathbf{T}_{WB}} \Sigma_B \text{Ad}_{\mathbf{T}_{WB}}^{T} \end{aligned} \]