控制相关线性系统理论
Source
Edit
History

第二章-状态空间描述

Catalogue
  1. 1. 1. 状态空间描述
    1. 1.1. 1.1. 输入-输出描述与状态空间描述的差异
    2. 1.2. 1.2. 状态、状态变量和状态向量
    3. 1.3. 1.3. 状态方程
    4. 1.4. 1.4. 输出方程
    5. 1.5. 1.5. 状态空间
    6. 1.6. 1.6. 线性系统状态空间表达式
    7. 1.7. 1.7. 线性定常系统状态空间表达式
    8. 1.8. 1.8. 线性系统和非线性系统
  2. 2. 2. 传递函数导出状态空间描述
    1. 2.1. 2.1. 给定单输入,单输出线性时不变系统的输入输出描述
    2. 2.2. 2.2. 给定单输入,单输出线性时不变系统的输入输出描述
    3. 2.3. 2.3. 给定单输入,单输出线性时不变系统的传递函数描述
    4. 2.4. 2.4. 由方框图描述导出状态空间描述
  3. 3. 3. 状态空间描述化标准型、约旦型
    1. 3.1. 3.1. 前提基础
      1. 3.1.1. 3.1.1. 特征多项式
      2. 3.1.2. 3.1.2. 特征值和特征向量
      3. 3.1.3. 3.1.3. 特征值的代数重数和几何重数
    2. 3.2. 3.2. 标准型
      1. 3.2.1. 3.2.1. 特征值两两互异(没有重根)
      2. 3.2.2. 3.2.2. 特征值有重根(但是仍然有n个独立特征向量)
    3. 3.3. 3.3. 约当规范形
  4. 4. 4. 状态空间===>传递函数矩阵
    1. 4.1. 4.1. 传递函数矩阵
    2. 4.2. 4.2. 传递函数严真性
    3. 4.3. 4.3. ABCD矩阵===>传递函数(重点在这里)
  5. 5. 5. 关于代数等价

1. 状态空间描述

1.1. 输入-输出描述与状态空间描述的差异

  1. 输入—输出描述(外部描述)

    • 用传递函数、微分方程表征;
    • 是系统的外部描述
    • 是对系统的不完全描述

  2. 状态空间描述(内部描述)

    • 用状态空间表达式表征
    • 是系统的内部描述
    • 是对系统的完全描述

1.2. 状态、状态变量和状态向量

  1. 状态

系统在时间域中的行为或运动信息的集合称为状态。 系统的状态是描述系统的过去、现在和未来行为的变量组,是用来完全表征系统时域行为的最小的一组变量，记为\(x_1(t),x_2(t)\cdots,x_n(t)\)

  1. 状态变量

是构成系统状态的变量,是指能完全表征系统行为的最小变量组中的每一个变量

  1. 状态向量

是由状态变量所构成的向量,即向量\(x(t)=[x_1(t),x_2(t),\cdots,x_n(t)]^T\)称为n维状态向量。给定t =t0 时的初始状态向量x(t0)及t≥t0 的输入向量u(t),则t≥t 0的状态由状态向量x(t)唯一确定。

  • 状态变量不是所有变量的总和
  • 状态变量的选取不唯一
  • 输出量可以选作状态变量
  • 输入量不允许选作状态变量
  • 状态变量有时是不可测量的
  • 状态变量是时域的

1.3. 状态方程

状态方程是描述内部变量\(x=[x_1,x_2,\cdots,x_n]^T\)与输入变量\(u=[u_1,u_2,\cdots,u_p]^T\)之间的因果关系数学表达是，常具有微分方程或差分方程的形式。

状态方程：描述系统状态变量与输入变量之间关系的一阶微分方程组(连续时间系统)或一阶差分方程组(离散时间系统)称为系统的状态方程。状态方程表征了系统由输入所引起的内部状态变化。

连续时间系统状态方程的一般形式为:

\[ \dot{x}(t)=f[x(t),u(t),t] \]

离散时间系统状态方程的一般形式为:

\[ x(t_{k+1})=f[x(t_k),u(t_k),t_k] \]

1.4. 输出方程

是表征系统内部变量\(x=[x_1,x_2,\cdots,x_n]^T\)和输入变量\(u=[u_1,u_2,\cdots,u_p]^T\)与输出变量\(y=[x_1,x_2,\cdots,x_n]^T\)之间的转换关系，就有代数方程形式

连续时间系统输出方程的一般形式为:

\[ y(t)=g[x(t),u(t),t] \]

离散时间系统输出方程的一般形式为:

\[ y(t_{k})=g[x(t_k),u_(t_k),t_k] \]

1.5. 状态空间

状态方程与输出方程的组合称为状态空间表达式,又称为动态方程或状态空间描述。

连续时间系统:

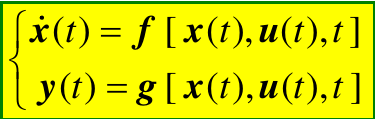
离散时间系统:

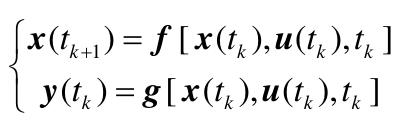
1.6. 线性系统状态空间表达式

状态方程与输出方程都是线性方程的系统是线性系统。线性系统的状态方程是一阶向量线性微分方程或一阶向量线性差分方程。

1.7. 线性定常系统状态空间表达式

线性系统的状态空间描述中,系统矩阵(A(t)或G(k))、控制矩阵(B(t)或H(k))、输出矩阵(C(t)或C(k))和前馈矩阵(D(t)或D(k))的每一个元素都是常数,则称该系统为线性定常系统(线性时不变系统), 否则为线性时变系统。

矩阵\(D\)描述了输入u不经状态变量x对输出y的直接影响,它不影响系统的动态过程,实质上是系统外部模型的一部分，因此,当利用状态模型来分析系统动态行为时,常假设D≡0,并不失对问题讨论的一般性。

1.8. 线性系统和非线性系统

泰勒展开，主要是求雅克比矩阵如下

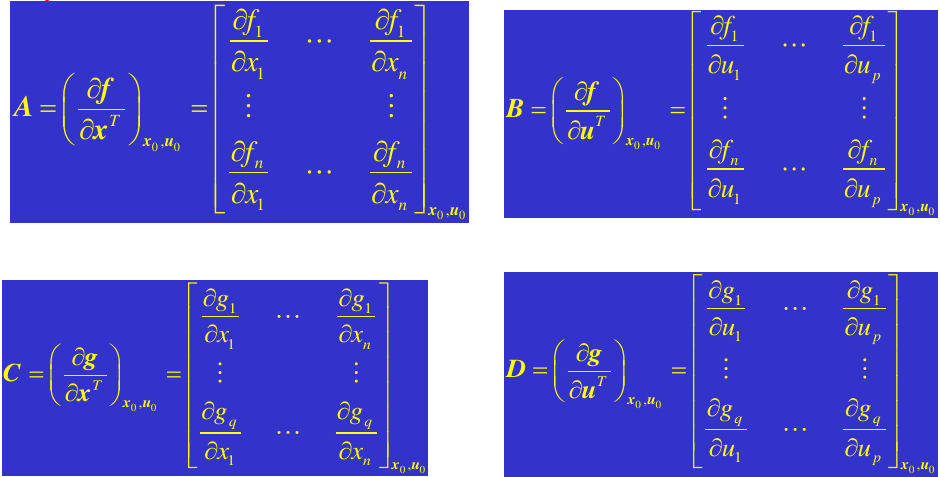
2. 传递函数导出状态空间描述

2.1. 给定单输入,单输出线性时不变系统的输入输出描述

给定单输入,单输出线性时不变系统的输入输出描述如下

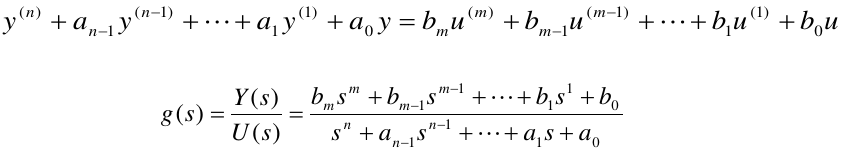
(1)m<n，系统为严真情形

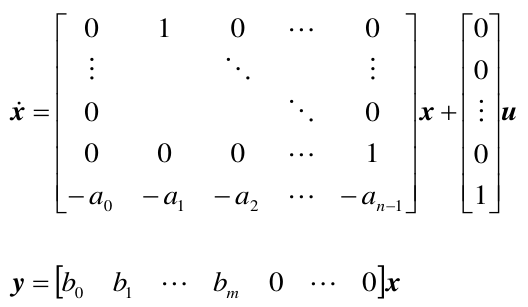
(2)m=n，系统为真情形

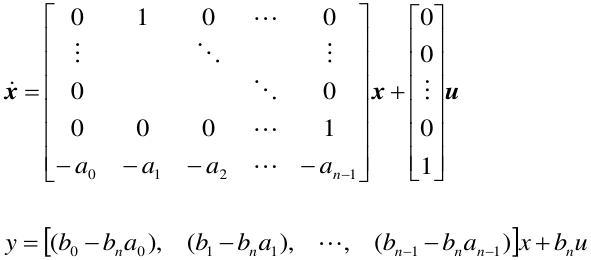
举例：

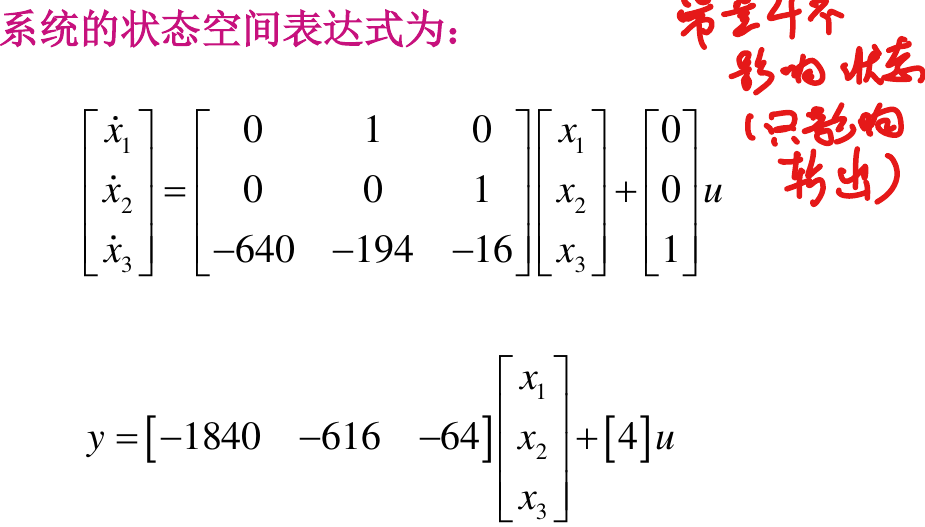
2.2. 给定单输入,单输出线性时不变系统的输入输出描述

(1)m=0情形

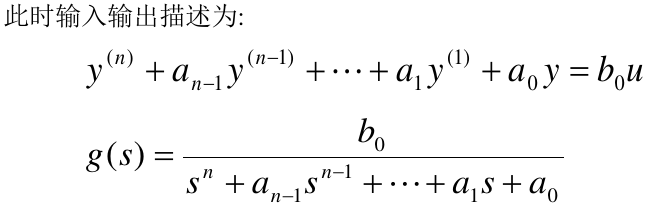
(2)m≠0情形

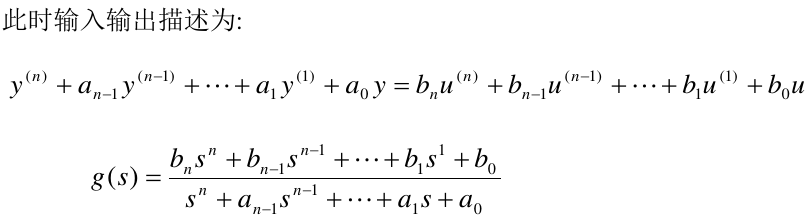
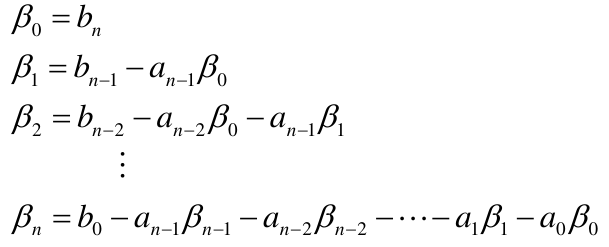
举例：

2.3. 给定单输入,单输出线性时不变系统的传递函数描述

给定单输入单输出线性时不变系统的传递函数描述为

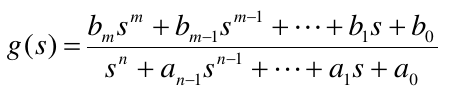
极点： 传递函数中，分母方程的根

要求，极点\(\lambda_1,\lambda_2,\cdots,\lambda_n\)都是两两互异的实数，即没有重根，可以分两种情况讨论

(1)m<n，系统为严真情形

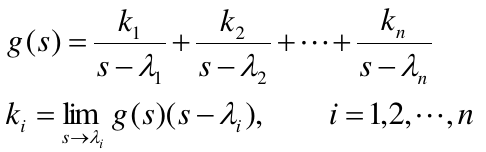
对应的状态空间描述为

\[ \begin{aligned} \dot{x}= \begin{bmatrix} \lambda_1, &~ & ~&~ \\ ~ & \lambda_1 & ~ &~ \\ ~ & ~ & \ddots & ~ \\ ~ & ~ & ~ & \lambda_n \end{bmatrix} x + \begin{bmatrix} k_1 \\ k_2 \\ \vdots \\ k_n \end{bmatrix} u \end{aligned} \]

\[ y=[1,1,\cdots,1]x \]

(1)m=n，系统为真情形

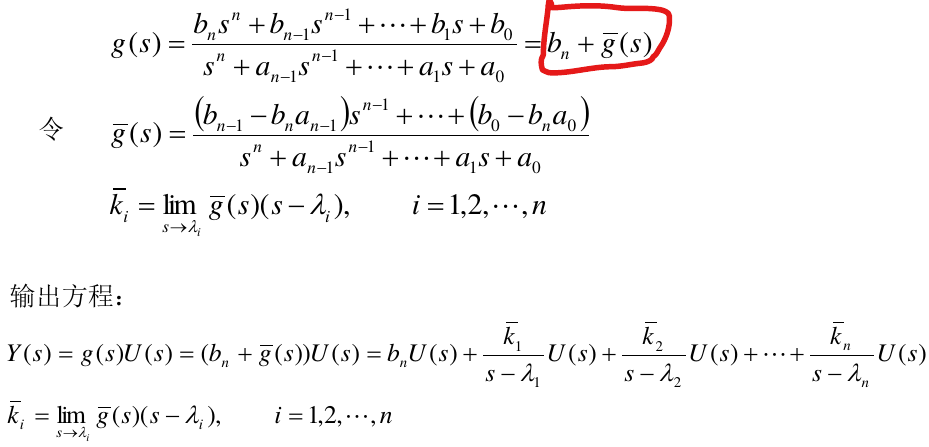
对应的状态空间描述为

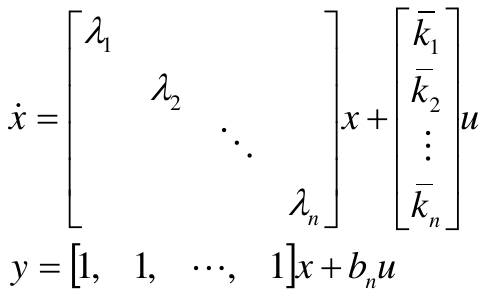
2.4. 由方框图描述导出状态空间描述

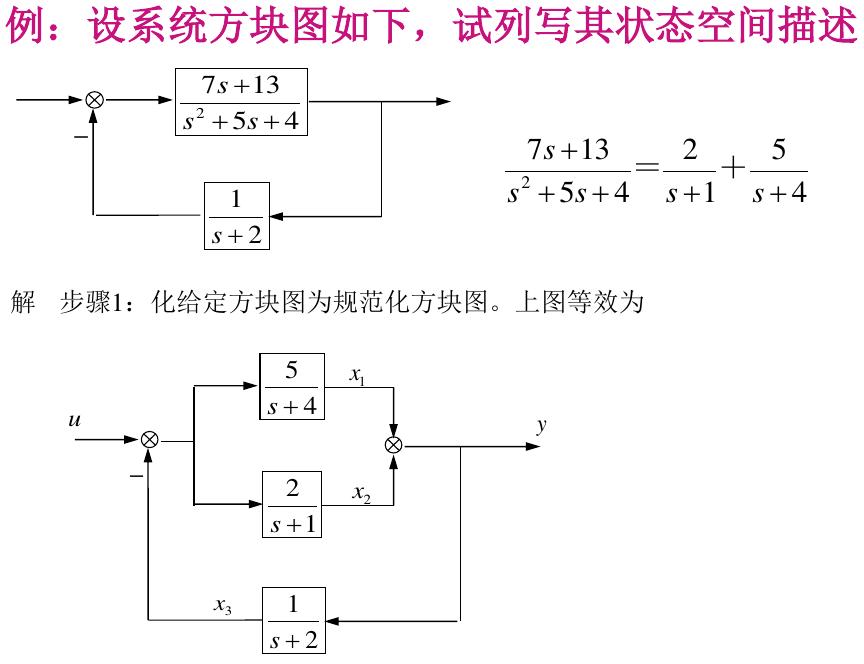
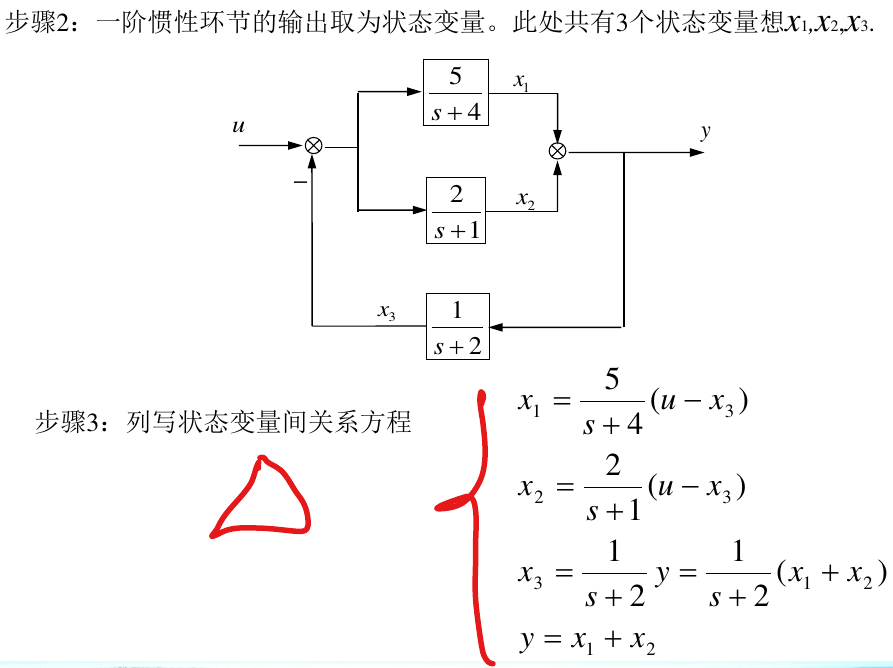
3. 状态空间描述化标准型、约旦型

3.1. 前提基础

3.1.1. 特征多项式

对于连续时间线性时不变系统\(\boldsymbol{\dot{x}=A x + B u}\)

  • 特征矩阵： \((sI-A)\)
  • 预解矩阵: \((sI-A)^{-1}\)
  • 特征多项式: \(\det(sI-A)\)

(1)特征多项式

\[ \alpha(s)=\det(sI-A)=s^n + \alpha_{n-1}s^{n-1}+\cdots + \alpha_1 s + \alpha_0 \]

其中，\(\alpha_0,\cdots,\alpha_{n-1}\)均为实数

(2)凯莱哈密顿定理

\[ \alpha(A)=A^n+ \alpha_{n-1}A^{n-1}+ \cdots + \alpha_1 A + \alpha_0 I =0 \]

其中，\(A\)为矩阵根

(3)莱弗勒算法——计算特征多项式

  • 通过迭代的方式，求出大常数矩阵A的特征多项式\((sI-A)\)

3.1.2. 特征值和特征向量

已知n阶线性定常系统的状态方程

\[ \dot{x}=Ax+Bu \]

系统的特征方程为:

\[ \det(sI-A)=0 \]

特征值为上述特征方程的根，即\(\{\lambda_1,\lambda_2,\cdots \lambda_n\}\)

将矩阵A的第i个特征值\(\lambda_i\)代入下列方程，如果存在一个非零向量\(v_i\)使得等式成立，那么该非零向量\(v_i\)就是关于特征值\(\lambda_i\)的特征向量。

\[ \begin{aligned} \lambda_i v_i = A v_i \\ \Longrightarrow (\lambda_i I -A)v_i = 0 \end{aligned} \]

3.1.3. 特征值的代数重数和几何重数

(1)代数重数\(\sigma_i\)

即某个特征值\(\lambda_i\)的重根数

(2)几何重数\(\alpha_i\)

即将特征值代入上面齐次方程组基础解系的解向量个数

\[ \alpha_i=n- rank(\lambda_i I -A) \]

特征值的几何重数\(\alpha_i\)表示了属于该特征值\(\lambda_i\)的线性无关特征向量的个数

  • 单特征值只对应一个特征向量(即\(\alpha_i=1\))
  • 有重根的特征值，可能对应多个独立的特征向量

只有当所有特征值的代数重数\(\sigma_i\)等于其几何重数\(\alpha_i\)时,矩阵A可以化为对角线规范形

3.2. 标准型

3.2.1. 特征值两两互异(没有重根)

可通过线性非奇异变换\(\bar{x}=P^{-1}x\)将状态方程化为对角型(标准型)

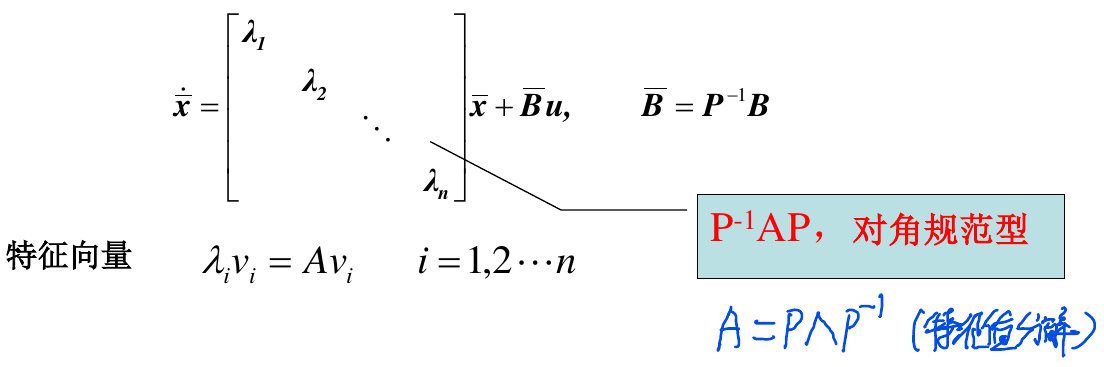
步骤:

  • 对A矩阵进行特征值分解\(A=P \Lambda P^{-1}\)
  • 那么，可得到化为标准型之后的\(\bar{A},\bar{B}\)
  • \(\bar{A}=P^{-1}AP\)
  • \(\bar{B}=p^{-1}B\)
  • 状态方程可重写为\(\dot{x}=\bar{A}x+\bar{B}u\)

例子1

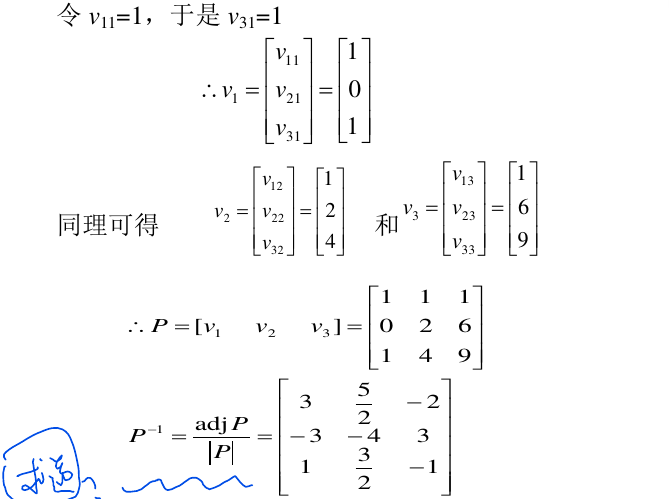
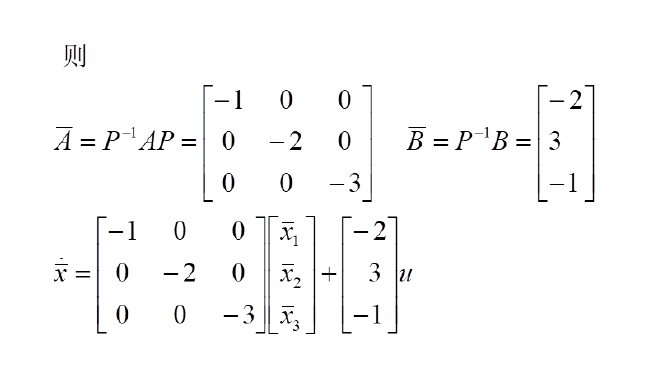
(特例)友矩阵形式

那么，可以直接写出变换矩阵P，不用进行特征值分解了

直接写出矩阵P

3.2.2. 特征值有重根(但是仍然有n个独立特征向量)

状态方程中的矩阵A虽然有重根，但是仍然有n个独立的特征向量，此时仍然可以化为对角标准型

例子

小结

两种情况可以化为对角标准型

  • 系统矩阵A的n个特征值两两互异
  • 系统矩阵A有重特征值，且所有特征值的几何重数都等于其代数重数

在对角线规范形下,系统矩阵是以特征值为元素的一个对角线矩阵,这意味着系统状态在对角线规范形下,系统各个状态变量之间实现了完全解耦

3.3. 约当规范形

当矩阵A有重根，并且独立向量个数\(<n\)，此时矩阵A不能化为对角型，但是可以化成约旦(Jordan)规范型

例子1

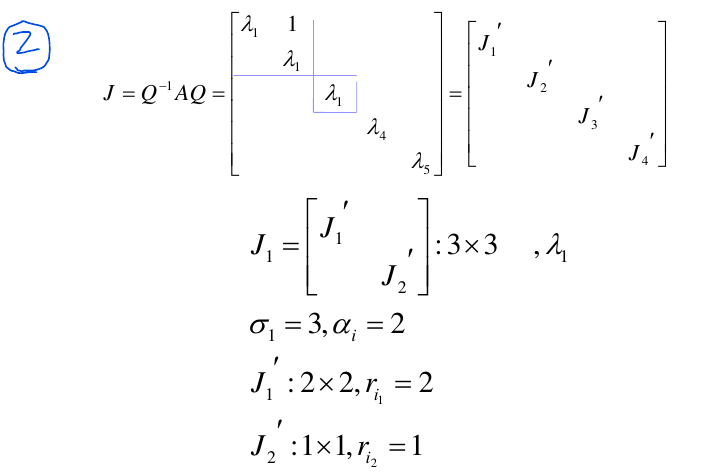
例子2

(特例)友矩阵形式

4. 状态空间===>传递函数矩阵

4.1. 传递函数矩阵

定义:

  1. 单输入单输出

单输入单输出线性时不变系统,在零初始条件下,输出变量拉普拉斯变换和输入变量拉普拉斯变换之比,称为系统的传递函数,即

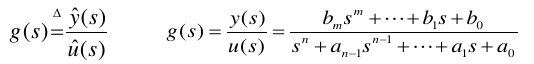
  1. 多输入多输出

多输入多输出线性时不变系统,在零初始条件下,输出变量拉普拉斯变换和输入变量拉普拉斯变换因果关系,即

4.2. 传递函数严真性

4.3. ABCD矩阵===>传递函数(重点在这里)

考虑连续时间线性时不变系统

\[ \begin{aligned} \dot{x}=Ax+Bu \\ y=Cx+Du \\ \\ \Longrightarrow G(s)=C(sI-A)^{-1}B+D \end{aligned} \]

计算机进行迭代计算，避免求逆的算法:

5. 关于代数等价

  • 两个系统为代数等价的必要条件是它们具有相同的维数
  • 同一系统采用不同的状态变量组所导出的两个状态空间描述之间,必然是代数等价的
  • 代数等价系统具有相同的传递函数矩阵,但相反的情况却不一定成立
  • 代数等价系统具有相同的特征值

系统经过线性非奇异变换后,不会改变系统原有特性(包括系统特征值、传递函数矩阵、可控性、可观性等),这就是所谓的线性非奇异变换的不变特性