占用栅格更新过程
静态二值贝叶斯滤波
机器人技术中的某些问题表达为不随时间变化的二值状态的最优估计间题。这些问题通过二值贝叶斯滤波 (binary Bayes filter) 来阐述。
如果一个机器人从传感器测量的序列中估计环境的一个固定的二值数,此时这类问题就产生了。例如,一个机器人可能想知道门是开着的还是关着的,并认为在检测期间门的状态不改变。
更新算法
当状态静止时,置信度就仅是测量的函数:

这里状态有两种:
- \(x\)
- \(\neg x\)
具体来说,有
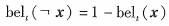
状态 x 不含时间项反映了状态不会改变的事实
自然的,这类二值估计问题可以利用程序 4. 1 的离散贝叶斯滤波来处理。但是,置信度通常由一个概率比的对数 (log odds ratio)来实现。状态 x 的概率比(odds) 定义为此事件的概率除以该事件不发生的概率
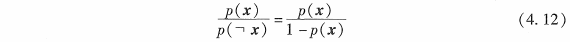
概率对数就是这个表达式的对数
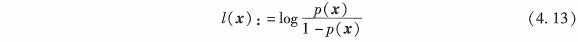
逆向公式,即置信度\({bel}_t(x)\)可以根据概率比对数\(l_t\)通过下面的方程来求得: :
概率对数将(0,1)映射到\(-\infty\) ~ \(\infty\),用于更新以概率对数表示的置信度的贝叶斯滤波计算很简洁。它避免了概率接近0或1引起的截断间题。
程序 4.2给出了其基本的更新算法。这种算法是加法。
事实上,任何对测量做出反应的变量的递增和递减都可以解释为贝叶斯滤波的概率对数形式。该二值贝叶斯滤波利用一个反向测量模型 (inverse measurement model) \(p(x|z_t)\)代替熟 悉的前向模型\(p(z_i|x)\) 。反向测量模型将关于(二值)状态变量的一个分布指定为测量\(z_t\)的一个函数。

反向模型经常用于测凰比二值状态更复杂的情况。这种情况的一个实例就是:
从相机图像中估计门是否为关的问题。这里状态很简单,但需要进行所有测量的空间却是很大的。通过设计一个函数根据相机图像来计算门为关着的概率, 要比描述所有相机图像中显示门为关着的分布更容易些。换旬话说,实现一个反向传感器模型比前向传感器模型更容易。
具体证明
根据贝叶斯公式及马尔可夫假设:
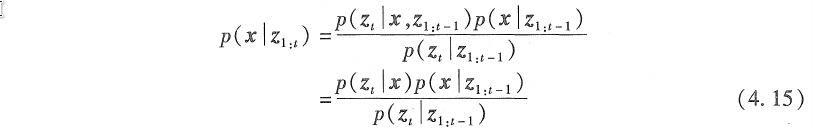
将贝叶斯准则应用于测量模型\(p(z_t|x)\)
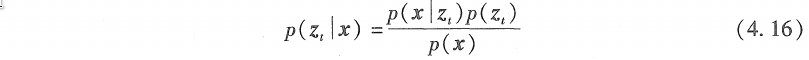
将上述两式结合,得到:
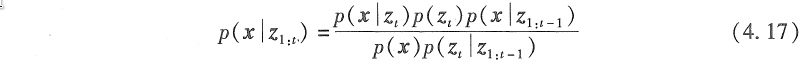
对于对立事件\(\neg x\),可得:
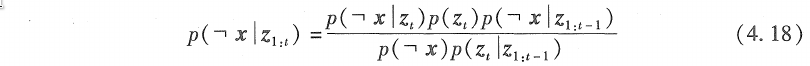
用式 (4. 18)除以式 (4. 17) 可以将各种难以计算的概率抵消:
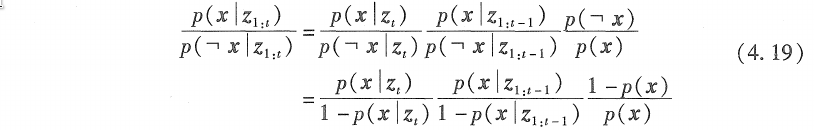
对上式两边同时取对数,用\(l_t(x)\)表示,即为置信度 \({bel}_t (x)\)的概率比对数\(log \frac{p(x|z_{1:t})}{1-p(x|z_{1:t})}\),有:
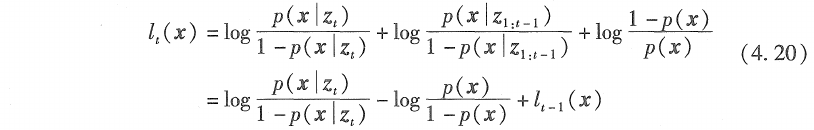
这里 \(p(x)\) 是状态 x 的先验 (prior) 概率。在式 (4. 20)中, 每个测最更新涉及先验(以概率对数形式)的求和。先验也定义为处理传感器测量前的初始置信度的概率对数: