Camera与单线激光标定

Catalogue

1. 1. Camera-单线激光标定
   1. 1.1. 1. 前言
   2. 1.2. 2.理论
      1. 1.2.1. 2.1 基于平面约束的相机激光标定算法
      2. 1.2.2. 2.1.2 2D 激光和相机外参数初始值求解
      3. 1.2.3. 2.1.3 3D 激光和相机外参数初始值求解
      4. 1.2.4. 2.1.4 联合优化进行调优
      5. 1.2.5. 2.2 推论：所有平行的平面提供的约束等价
      6. 1.2.6. 2.3 拓展：标定板的边界约束
   3. 1.3. 3. 实践
      1. 1.3.1. 3.1 代码梳理和上手操作
      2. 1.3.2. 3.2 仿真代码的特别说明
      3. 1.3.3. 3.2.1 系统可观性的判断
      4. 1.3.4. 3.2.2 利用仿真代码验证平行平面提供的约束等价
      5. 1.3.5. 3.2.2 利用仿真代码指导采集数据：如何充分旋转标定板
   4. 1.4. 4. 结语
   5. 1.5. 5. 参考文献
   6. 1.6. 作者简介

Camera-单线激光标定

本文来源于 《标定系列三 | 实践之Camera-Lidar标定》

1. 前言

从理论上看，相机和激光之间外参数的标定原理非常简单，但在实际标定过程中，特别是一个初学者采集数据进行标定时，却发现标定结果非常不理想。如何采集有效的标定数据（何种运动轨迹，如何晃动标定板）对于激光相机标定而言非常重要。

读完本文，你会发现原来采集数据时标定板和传感器之间只做纯粹的平移运动是没有意义的。本文也对相机激光标定的一些基础知识和小细节进行讨论，主要贡献点有三：

1. 从理论开始对激光（单线、多线都适用）和相机外参数的标定进行简要推导（公式多但简单），然后给出一些可以提升标定精度的改进建议。
2. 给出一个简单的开源代码对上述标定原理进行实践。
3. 提供一个仿真程序，可以直观感受标定数据对系统可观性的影响。

2.理论

通常，标定激光和相机之间的外参数有两类方法：一类是利用 3D-3D 的约束，即利用激光测量的三维激光点 (3D) 和相机测量的标定板三维坐标 (3D) 两者来构建约束；另一类是利用 3D-2D 的约束，即利用激光测量的三维激光点 (3D) 和图像二维特征（2D、点特征、线段特征）来构建约束。

本文主要讲解利用 3D-3D 约束来进行外参数标定的方法，而 3D-2D 这一方法和 PnP 或 PnL 问题类似，这里不做展开。另外，标定过程的通常做法是先利用少量观测求解外参数的初始值，然后利用多帧数据的约束进行最小二乘优化对初始值进行 refine。接下来，将按照这个逻辑对标定算法进行讲解并推荐一些改进的算法。

2.1 基于平面约束的相机激光标定算法

如下图所示，相机可以通过标定板平面的二维码或棋盘格来计算标定板平面在相机坐标系下的表示。同时，激光发出的光束落在标定板平面上（图中红点），利用激光点在激光坐标系下的坐标和平面方程在相机坐标系下的坐标，构建点在平面上的约束从而求解外参数。

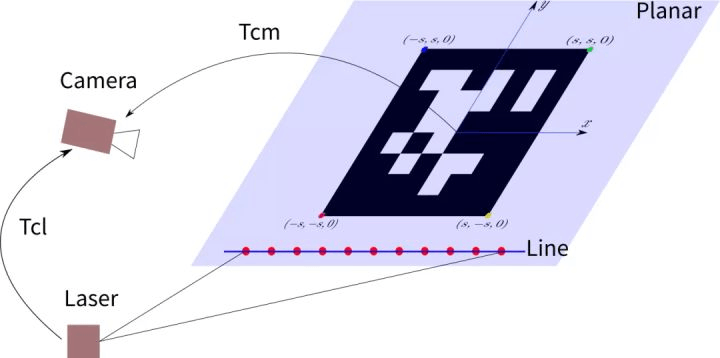
2.1.1 平面约束

假设标定板平面在相机坐标系$c$中的参数为$\pi^{c}=\left[\mathrm{n}^{c}, d\right] \in \mathbb{R}^{4}$，其中$\mathrm{n}^{c} \in \mathbb{R}^{3}$是平面法向量，$d$是相机坐标系原点到平面的距离。

假设平面上的一个三维空间点在相机坐标系的坐标为$\mathbf{P}^{c} \in \mathbb{R}^{3}$，那么该点满足如下约束方程：

$$\mathbf{n}^{c \top} \mathbf{P}^{c}+d=0$$

假设从激光雷达坐标系$l$到相机坐标系$c$的旋转和平移表示为：$\mathbf{R}_{c l}, \mathbf{t}_{c l}$，一旦知道激光坐标系中的某个激光点$\mathbf{P}^{l}$落在标定板上，则通过点在平面上的约束可以构建关于外参的方程（1）：

$$\mathbf{n}^{c \top}\left(\mathbf{R}_{c l} \mathbf{P}^{l}+\mathbf{t}_{c l}\right)+d^{c}=0$$

上述方程能够提供一个约束，通过多个这样的约束就能求解外参数。求解时，一个直观的想法是利用 g2o 或者 ceres 等优化工具构建非线性最小二乘进行优化求解。但是对于非线性最小二乘问题，需要知道外参数的一个初始值，如果初始值不准确，则有可能会优化到局部最小值。因此，一个合理的求解流程应该是闭式解提供初始值，对该初始值利用多帧数据进行优化，得到更准确的标定结果。

虽然平面约束对于 2D 激光和 3D 激光而言是一样的，但 2D 激光和 3D 激光闭式求解外参数的方式稍有不同。因为 3D 激光的激光点更多，从而可以直接计算激光点云的法向量，利用这个法向量简化外参数计算流程，下文将详述。接下来，介绍 2D 激光和相机外参数的求解。

2.1.2 2D 激光和相机外参数初始值求解

这里主要参考 2004 年 Zhou 等人的论文【1】，该论文是比较早期的工作，求解思路清晰。论文中估计的参数为从相机坐标系到激光坐标系的变换矩阵$\mathbf{R}_{c l},\mathbf{t}_{c l}$，因此，激光点从激光雷达坐标系到相机坐标系的变换如下：

$$\mathbf{P}^{c}=\mathbf{R}_{l c}^{\top}\left(\mathbf{P}^{l}-\mathbf{t}_{l c}\right)$$

考虑到，激光为 2D 激光，激光束形成的平面不妨假设为 xy 平面，即$z=0$，此时，激光点形如$\mathbf{P}^{l}=[x, y, 0]^{\top}$，因此，上面的坐标变换可以写成更紧凑（矩阵、向量相乘）的形式：

$$\mathbf{P}^{c}=\mathbf{R}_{l c}^{\top}\left(\left[\begin{array}{l} x \\ y \\ 0 \end{array}\right]-\mathbf{t}_{l c}\right)=\underbrace{\mathbf{R}_{l c}^{\top}\left[\begin{array}{lll} 1 & 0 & \\ 0 & 1 & -\mathbf{t}_{l c} \\ 0 & 0 & \end{array}\right]}_{\mathbf{H} }\left[\begin{array}{l} x \\ y \\ 1 \end{array}\right]=\mathbf{H} \overline{\mathbf{P} }^{l}$$

因此，将紧凑形式的坐标变换代入公式（1），得到：

$$\mathbf{n}^{c \top} \mathbf{H} \overline{\mathbf{P} }^{l}=-d^{c}$$

如果把 3 乘 3 的$\mathbf{H}$矩阵当做新的未知量（ 9 个参数）进行估计，那上述约束就变成了一个线性最小二乘问题。

对于单线激光而言，一帧激光可以提供两个有效约束（直线上两个点在平面上即能确定直线在平面上），因此大于等于 5 帧激光（不同姿态）就能得到 10 个以上的约束，来直接求得 9 参数的$\mathbf{H}$矩阵，然后还原出$\mathbf{R}_{c l}, \mathbf{t}_{c l}$：

$$\begin{aligned} \mathbf{R}_{l c} &=\left[\begin{array}{lll} \mathbf{h}_{1} & \mathbf{h}_{2} & \mathbf{h}_{1} \times \mathbf{h}_{2} \end{array}\right]^{\top} \\ \mathbf{t}_{l c} &=-\left[\begin{array}{lll} \mathbf{h}_{1} & \mathbf{h}_{2} & \mathbf{h}_{1} \times \mathbf{h}_{2} \end{array}\right]^{\top} \mathbf{h}_{3} \end{aligned}$$

简单推导：

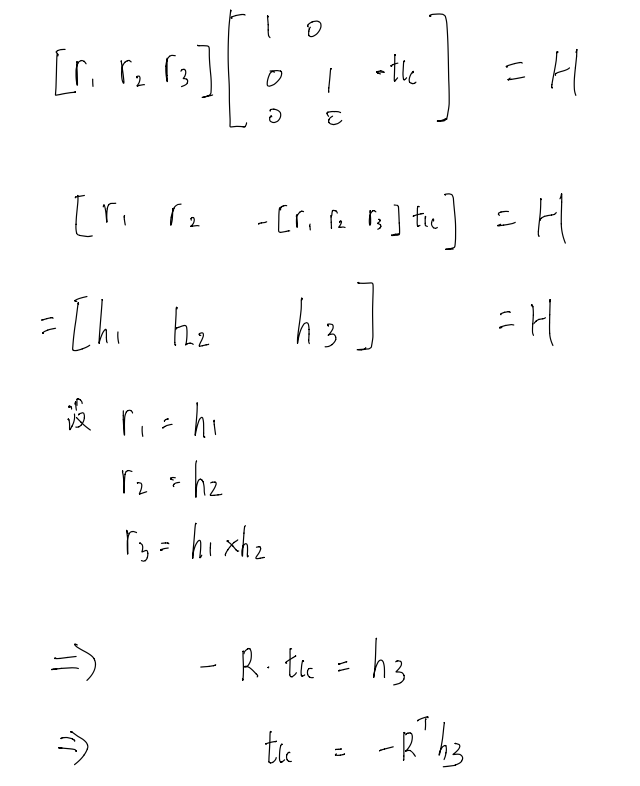
但是，利用上述方式求得的旋转矩阵并不满足旋转矩阵的性质$\mathbf{R}^{\top} \mathbf{R}=\mathbf{I}_{3 \times 3}$，假设期望的旋转矩阵为$\hat{\mathbf{R} }_{l c}$，则可通过计算带约束的最小化F范数问题来估计出期望的旋转矩阵$\hat{\mathbf{R} }_{l c}$：

$$\arg \min \left\|\hat{\mathbf{R} }_{l c}-\mathbf{R}_{l c}\right\|_{F}, \quad \text { subject to } \hat{\mathbf{R} }_{l c}^{\top} \hat{\mathbf{R} }_{l c}=\mathbf{I}$$

其意义为：找一个最接近$\mathbf{R}_{c l}$又满足旋转矩阵质$\mathbf{R}^{\top} \mathbf{R}=\mathbf{I}_{3 \times 3}$的矩阵$\hat{\mathbf{R} }_{l c}$作为要求的旋转矩阵。此外，参考文献【2，3】给出了闭式解。

然而，文献【3】指出，上述方式求解的精度不高，实际应用过程并不推荐，正如多视角几何中估计本征矩阵E矩阵一样，也分为 DLT 算法（直接计算 8 个参数）和其他算法。

因此，在这里，优雅的方式应该是直接闭式求解 6 自由度的外参数，即旋转矩阵只用 3 个参数而不是上述方法中先估计 9 个参数。参考文献【4】给出了一种闭式求解 6 自由度外参数的方法，由于估计的参数为 6 ，因此需要的最少激光观测变成了 3 帧（每帧提供两个有效约束）。

2.1.3 3D 激光和相机外参数初始值求解

跟 2D 激光的单线数据仅仅能提供一条线相比， 3D 激光的多线数据能提供点云面的信息。因此，同样是利用激光点在标定板平面上这个约束，3D 激光的约束可以比 2D 激光更多一个。

3D 的激光的点云平面和标定板平面重合，意味着单帧 3D激光提供的有效约束为 3 个（即点云平面上的3个点落在标定板平面上），从而可以用 3 个激光点来构建公式 (1) 的约束。这样两帧激光（6个约束）就能求解外参数了，求解方式可以利用前面 2D 激光所描述的方法（则同样存在 DLT 方法初始值不准的问题）。

这里给出了 3D 激光求解外参数的另一个思路，该方法中，求解的旋转矩阵能自然地满足旋转矩阵的性质：$\mathbf{R}^{\top} \mathbf{R}=\mathrm{I}, \operatorname{det}(\mathrm{R})=1$。

将单帧激光的点云平面和标定板平面重合的约束进行简单置换，如下公式（2）：

$$\begin{aligned} \mathbf{R}_{c l} \mathbf{n}^{l} &=\mathbf{n}^{c} \\ \mathbf{n}^{c \top}\left(\mathbf{R}_{c l} \mathbf{P}^{l}+\mathbf{t}_{c l}\right)+d^{c} &=0 \end{aligned}$$

公式 (2) 中的两个方程中，第一个方程能提供 2 个有效约束，第二个方程提供 1 个有效约束。虽然公式 (2) 和三个点落在平面上的物理意义一样，但是，公式 (2) 中第一个方程只和旋转矩阵有关，和平移无关。意味着可以先求解旋转矩阵，再线性求解平移向量，从而简化参数估计。

当激光帧数 N 大于等于 2 时，可以求解如下非线性最小二乘问题来计算旋转矩阵，如下公式（3）：

$$C=\sum_{i=1}^{N}\left\|\mathbf{n}_{i}^{c}-\mathbf{R}_{c l} \mathbf{n}_{i}^{l}\right\|^{2}$$

这里基于参考文献【5】介绍上述问题的通用解法。将公式 (3) 进行展开有：

$$\begin{aligned} C &=\sum_{i=1}^{N}\left(\mathbf{n}_{i}^{c}-\mathbf{R}_{c l} \mathbf{n}_{i}^{l}\right)^{\top}\left(\mathbf{n}_{i}^{c}-\mathbf{R}_{c l} \mathbf{n}_{i}^{l}\right) \\ &=\sum_{i=1}^{N}\left(\mathbf{n}_{i}^{c \top} \mathbf{n}_{i}^{c}+\mathbf{n}_{i}^{l \top} \mathbf{n}_{i}^{l}-2 \mathbf{n}_{i}^{c \top} \mathbf{R}_{c l} \mathbf{n}_{i}^{l}\right) \end{aligned}$$

由于两个坐标系下的平面法向量$n$已知，因此，最小化损失函数 C 转化成最大化如下目标：

$$\begin{aligned} F &=\sum_{i=1}^{N} \mathbf{n}_{i}^{c \top} \mathbf{R}_{c l} \mathbf{n}_{i}^{l} \\ &=\operatorname{Trace}\left(\sum_{i=1}^{N} \mathbf{R}_{c l} \mathbf{n}_{i}^{l} \mathbf{n}_{i}^{c \top}\right)=\operatorname{Trace}(\mathbf{R} \mathbf{H}) \end{aligned}$$

此处应用了迹的性质 （跟ICP的推导一样） - 常数等于常数的迹 - 迹内的元素顺序可交换

其中，这里引入了一个中间矩阵$\mathbf{H}$

$$\mathbf{H}=\sum_{i=1}^{N} \mathbf{n}_{i}^{l} \mathbf{n}_{i}^{c \top}$$

下面还要用到一个引理：

对于任意的正定矩阵$\mathrm{AA}^{\top}$以及任意正交矩阵B，有下面的不等式成立：

$$\operatorname{Trace}\left(\mathbf{A} \mathbf{A}^{\top}\right) \geq \operatorname{Trace}\left(\mathbf{B A A}^{\top}\right)$$

接下来，回到之前的推导，我们对中间矩阵$\mathbf{H}$进行SVD分解，有：

$$\mathbf{H}=\mathbf{U} \mathbf{\Lambda} \mathbf{V}^{\top}$$

其中，$\mathbf{U}, \mathbf{V}$是3x3矩阵，$\mathbf{\Lambda}$ 是3x3的对角阵，其元素非负。

下面做一个假设，令$\mathbf{R}_{c l}=\mathbf{V} \mathbf{U}^{\top}$，那么上面的$\operatorname{Trace}(\mathbf{R} \mathbf{H})$可以重写为：

$$\begin{aligned} \mathbf{R}_{c l} \mathbf{H} &=\mathbf{V} \mathbf{U}^{\top} \mathbf{U} \mathbf{\Lambda} \mathbf{V}^{\top} \\ &=\mathbf{V} \mathbf{\Lambda} \mathbf{V}^{\top} \end{aligned}$$

此时，$\mathbf{R}_{c l} \mathbf{H}$是对称的正定矩阵，这时候就要使用前面埋下的引理，来证明$\mathbf{R}_{c l}=\mathbf{V} \mathbf{U}^{\top}$即为解。

反证：如果$\mathbf{R}_{c l}=\mathbf{V} \mathbf{U}^{\top}$不是解，那么它和正确解之前存在一个增量旋转矩阵$\mathbf{R}_{\Delta}$，即$\mathbf{R}_{c l}=\mathbf{R}_{\Delta}\mathbf{V} \mathbf{U}^{\top}$ ，此时根据上面的引理，可得，这个解不会使得损失函数F的值取最大，因为：

$$\operatorname{Trace}\left(\mathbf{R}_{c l} \mathbf{H}\right) \geq \operatorname{Trace}\left(\mathbf{R}_{\Delta} \mathbf{R}_{c l} \mathbf{H}\right)$$

最后，还需要做旋转矩阵性质的判断，如果$\operatorname{det}\left(\mathbf{V} \mathbf{U}^{\top}\right)=1$，则说明所求得的正交矩阵$\mathbf{R}_{c l}=\mathbf{V} \mathbf{U}^{\top}$是旋转矩阵。如果$\operatorname{det}\left(\mathbf{V} \mathbf{U}^{\top}\right)=-1$，则说明这个正交矩阵是镜面反射矩阵，不是旋转矩阵。幸运的是，在实际应用中，采集的多帧不同姿态下的激光数据并不会出现镜面反射矩阵的情况。

在旋转矩阵已知的情况下，利用公式 (1) 就可以求解平移向量$\mathbf{t}_{c l}$，这时候求解只涉及到平移，是个线性最小二乘问题$\mathbf{A} \mathbf{t}_{c l}=\mathbf{b}$，可以使用闭式解求解。

最后，关于上面使用的引理$\operatorname{Trace}\left(\mathbf{A} \mathbf{A}^{\top}\right) \geq \operatorname{Trace}\left(\mathbf{B A A}^{\top}\right)$，证明如下：

假设$a_{i}$是矩阵$\mathbf{A}$的第i列，则有：

$$\begin{aligned} \operatorname{Trace}\left(\mathbf{B A} \mathbf{A}^{\top}\right) &=\operatorname{Trace}\left(\mathbf{A}^{\top} \mathbf{B} \mathbf{A}\right) \\ &=\sum_{i} \mathbf{a}_{i}^{\top}\left(\mathbf{B} \mathbf{a}_{i}\right) \end{aligned}$$

根据Cauchy-Schwarz不等式$x y \leq \sqrt{x^{2} y^{2} }$，且矩阵B为正交矩阵，有：

$$\mathbf{a}_{i}^{\top}\left(\mathbf{B} \mathbf{a}_{i}\right) \leq \sqrt{\left(\mathbf{a}_{i}^{\top} \mathbf{a}_{i}\right)\left(\mathbf{a}_{i}^{\top} \mathbf{B}^{\top} \mathbf{B a}_{i}\right)}=\mathbf{a}_{i}^{\top} \mathbf{a}_{i}$$

因此，可证得：

$$\operatorname{Trace}\left(\mathbf{A} \mathbf{A}^{\top}\right)=\sum_{i} a_{i}^{\top} a_{i} \geq \operatorname{Trace}\left(\mathbf{B A} \mathbf{A}^{\top}\right)$$

2.1.4 联合优化进行调优

通过上述方式计算出外参数的初始值之后，再对采集的N组数据进行联合优化得到最优估计，假设第i帧激光有$N_{i}$个激光点落在标定板上，同时第i帧激光时刻下对应的标定板平面方程在相机坐标系的表示为$\left[\mathbf{n}_{i}^{c}, d_{i}^{c}\right]^{\top}$，则问题可以描述为：

$$\hat{\mathbf{R} }_{c l}, \hat{\mathbf{t} }_{c l}=\arg \min _{\mathbf{R}_{cl}, t_{cl} } \sum_{i=1}^{N} \frac{1}{N_{i} } \sum_{m=1}^{N_{i} }\left\|\mathbf{n}_{i}^{c \top}\left(\mathbf{R}_{c l} \mathbf{P}_{i m}^{l}+\mathbf{t}_{c l}\right)+d_{i}^{c}\right\|^{2}$$

优化过程中，对于旋转矩阵$\mathbf{R}_{c l}$，可以使用 SO3 的参数化方式，也可以采用四元数的参数化方式。优化方法 (LM算法），雅克比的推导等知识点这里不再赘述，大家可以对照开源的代码自行推导验证雅克比。

2.2 推论：所有平行的平面提供的约束等价

前面求解过程中，是假设采集的数据足够有效，即采集了不同姿态下标定板和激光数据的数据。那么，如何摆放标定板来采集数据是有效的呢？这里将证明只平移标定板对标定没有意义，标定过程中只需要旋转标定板。推荐阅读参考文献【6】

平移标定板意味着不同时刻之间的标定板平面是平行的。假设有两个平行平面$\pi_{1}, \pi_{2}$，它们在相机坐标系中的参数分别为$\left[\mathbf{n}^{c}, d_{1}^{c}\right]^{\top}$和$\left[\mathbf{n}^{c}, d_{2}^{c}\right]^{\top}$。另外，假设在激光坐标系下，激光测量了两个平面上任意的一个点$\mathbf{P}_{1}^{l}, \mathbf{P}_{2}^{l}$，考虑点在平面上的约束有：

$$\begin{array}{l} \mathbf{n}^{c \top}\left(\mathbf{R}_{c l} \mathbf{P}_{1}^{l}+\mathbf{t}_{c l}\right)+d_{1}^{c}=0 \\ \mathbf{n}^{c \top}\left(\mathbf{R}_{c l} \mathbf{P}_{2}^{l}+\mathbf{t}_{c l}\right)+d_{2}^{c}=0 \end{array}$$

通过简单的变换，可以发现上面两个等式能够相互转换，即表示平行的平面只能提供相同的约束信息。

变换如下：首先将$\mathbf{n}^{c \top} \mathbf{t}_{c l}$这部分从两个等式中移除，然后有：

$$\begin{aligned} & \mathbf{n}^{c \top} \mathbf{R}_{c l} \mathbf{P}_{1}^{l}+d_{1}^{c} \\ =& \mathbf{n}^{c \top} \mathbf{R}_{c l}\left(\mathbf{P}_{2}^{l}+\mathbf{P}_{1}^{l}-\mathbf{P}_{2}^{l}\right)+d_{2}^{c}+d_{1}^{c}-d_{2}^{c} \\ =& \mathbf{n}^{c \top} \mathbf{R}_{c l} \mathbf{P}_{2}^{l}+d_{2}^{c}+\left(\mathbf{n}^{c \top} \mathbf{R}_{c l}\left(\mathbf{P}_{1}^{l}-\mathbf{P}_{2}^{l}\right)+d_{1}^{c}-d_{2}^{c}\right) \\ =& \mathbf{n}^{c \top} \mathbf{R}_{c l} \mathbf{P}_{2}^{l}+d_{2}^{c} \end{aligned}$$

其中，$\mathbf{n}^{c \top} \mathbf{R}_{c l}\left(\mathbf{P}_{1}^{l}-\mathbf{P}_{2}^{l}\right)$和$d_{1}^{c}-d_{2}^{c}$表示两个平面之间的距离，式中，它们两个方向符号相反可以抵消。

由此证明：所有平行的平面物体提供的约束是等价的。这意味着：采集数据用于标定时，如果只平移标定板来采集数据，那就做了很多无用功。比如不断平移标定板采集了 100 个时刻的数据，那这 100 次的数据仅相当于 1 次有效数据。所以，采集标定数据时，只要不断旋转标定板采集数据就足够了，而不是不断平移。

2.3 拓展：标定板的边界约束

上述标定过程只利用了平面标定板的平面约束来进行标定，也清楚了这个约束对于单次测量而言，其提供的有效约束 (2个或者3个) 不足以完成单帧标定，而采集多帧数据又容易由于采集轨迹不充分，导致外参在某些维度标定不好。

因此，如果标定板一次就能够提供 6 个以上的约束，那意味着单帧数据就能完成标定，并且多约束的加入能够提升标定精度。这方面的工作有两类方式，一种是改变标定板的形状，比如两个垂直的标定板，或者三个垂直的标定板，V 形标定板等。

另一种是充分利用其他约束，比如激光点落在标定板边缘直线上（标定板边缘的直线方程以及哪个激光点落在上面是可以计算出来的）。这里不作详细的推导和解释，仅推荐两篇2018年的经典论文，见参考文献【6】和参考文献【7】。论文【6】是利用标定板的边缘直线约束来标定3D激光，论文【7】对2D激光的多种标定板的有效约束进行了充分讨论。

3. 实践

根据上述的理论推导，本文完成了一个简单的 2D 激光和相机之间外参数的标定代码：

https://github.com/MegviiRobot/CamLaserCalibraTool

3.1 代码梳理和上手操作

关于数据的采集，标定板的制作，标定的流程以及标定结果等上手操作细节在项目的 README.md 里已经进行了详细说明，这里对系统中的几个主要文件进行简单梳理，帮助大家更快熟悉代码。

大家关注的外参数的代码大多都在 src 文件夹里的 LaserCamCalCeres.cpp，其中：

• CamLaserCalClosedSolution() ：闭式求解外参数初始值。
• CamLaserCalibration() ：采用非线性最小二乘对初始值进行优化。

另外，比较重要的为 main 文件夹中的三个主程序：

• kalibratag_detector_node.cpp : 相机利用二维码或者棋盘格估计标定板平面和相机之间的姿态。
• calibr_offline.cpp : 处理激光数据（获取在标定板上的激光点云），读取事先处理好的相机姿态，利用这些数据构建平面约束进行外参数求解。
• calibr_simulation.cpp : 生成仿真数据，验证系统参数是否可观。后面小结讲着重说明。

3.2 仿真代码的特别说明

仿真代码可以帮助大家理解采集数据的有效性对标定结果的影响，对理解系统辨识（系统参数是否可观）非常有意义，因此在这里进行特别说明。

代码中的 GenerateSimData() 函数主要用来生成仿真数据，原理为利用激光射线和标定板平面相交，从而得到激光点在标定板上的三维坐标，通过不断变换标定板的姿态，得到多组有效数据（激光点云+标定板在相机中的姿态）用来完成标定。

其中标定板和相机之间的姿态保存在变量$\mathbf{R}_{c a}, \mathbf{t}_{c a}$，代码中采用利用随机数的方式来生成标定板姿态，并可以通过对标定板参数进行不同的设置来对系统的可观性进行验证。

3.2.1 系统可观性的判断

熟悉 VIO(visual inertial odometry) 系统也会熟知可观性问题。实际上，系统的可观性在线代控制理论中有专门论述，涉及到可观性矩阵等知识点，但是那套从线性系统出发的理论可能容易让大家迷惑。这里会从大家熟知的非线性优化求解的角度来简单描述可观性问题。

关于状态量参数是否可观的一个简单解释是：如果改变状态向量$\mathbf{X}$的值，系统对应的观测函数$\mathrm{f}(\mathrm{x})$不发生变化，即$\mathbf{f}(\mathbf{x})=\mathbf{f}\left(\mathbf{x}^{\prime}\right)$，则说明系统在某些维度上不可观。直观的理解就是，系统有无数个解从而使得状态量无法辨识。在非线性最小二乘问题中，通过构建误差函数利用高斯牛顿算法进行优化求解时，通常需要求解如下 normal equation：

$$\mathbf{J}^{\top} \mathbf{J} \delta \mathbf{x}=-\mathbf{J}^{\top} \mathbf{r} \Rightarrow \mathbf{H} \delta \mathbf{x}=\mathbf{b}$$

其中，

• $\mathbf{J}$是残差对状态量求导的雅克比矩阵
• $\mathbf{r}$是利用约束构建的残差

如果系统求解过程中$\mathbf{H}$矩阵不满秩，假设其零空间为$\mathbf{N}$，有$\mathbf{H} \mathbf{N}=0$，意味着求解存在多个解：

$$\begin{array}{r} \mathbf{H} \delta \mathbf{x}=\mathbf{b} \\ \mathbf{H} \delta \mathbf{x}+\mathbf{H N}=\mathbf{b} \end{array}$$

即系统有无穷多个解$\delta \mathbf{x}+\lambda \mathbf{N}$使得残差最小，零空间$\mathbf{N}$的基底对应不可观的方向。所以可以通过判断$\mathbf{H}$矩阵的秩来判断系统的可观性，比如$\mathbf{H}$矩阵为 6 维的方阵，而秩等于 4，则意味着零空间维度为 2 ，有两个不可观的方向，这个结论在后面将用来指导采集数据。

那么，如果你熟悉 VIO，自然要问既然线性系统中的可观性矩阵和优化方法中的 H 矩阵都能够判断系统可观性？这两者之间存在什么样的联系呢？这里不再展开推导，推荐阅读参考文献【8】，读完第二章你将豁然开朗。

3.2.2 利用仿真代码验证平行平面提供的约束等价

为了生成平行的标定板平面，只需要把代码中的$\mathbf{R}_{c a}$设置成常数，如单位矩阵。这时，标定板只有平移，意味着生成的所有数据里标定板平行。编译并运行仿真程序后会有如下信息：

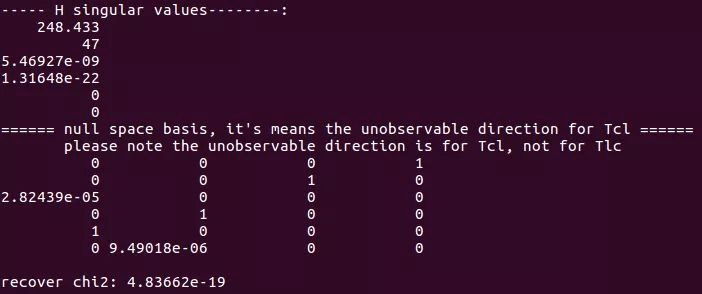
由于估计的外参数为 6 维，其中 H 矩阵的奇异值有 4 个接近 0，意味着只产生了两个维度的有效信息。这和之前的推论结论一致，即多帧数据中平行的标定板产生的约束等效于一帧，而单线激光落在平面上的有效约束为 2。

另外利用数值的方法计算了 H 矩阵的零空间基底，从图中可以看到最右边两列的两个基底，它们是对应平移 x,y 不可观，而左边两列对应的的两个基底为旋转矩阵角度的两个维度不可观。不可观基底对应的方向表示外参数对应的维度无法求出正确解。

3.2.2 利用仿真代码指导采集数据：如何充分旋转标定板

既然采集数据时只平移标定板不行，那是否意味着简单旋转一下标定板就可以了呢？比如标定板只绕着 y 轴旋转。这里可通过设置不同的旋转矩阵去验证 H 矩阵是否有零空间。通过简单修改代码（注释或反注释设置旋转矩阵的那几行代码），运行后会发现：标定时需要充分旋转 x 和 y 两个轴，标定过程中标定板只旋转一个轴一样会存在零空间基底。

这意味着拿着标定板旋转时，需要充分旋转 roll 和 pitch。更直白一点，假设在长方形的标定板中心画了个十字线，那请绕着十字线的两个轴充分旋转，比如绕着竖轴旋转，然后还要绕着横轴旋转。

4. 结语

至此，相机和激光标定从理论到实践就基本完成了。本文抛砖引玉，介绍了比较基础的标定原理，开源了相应的代码（包括求解代码、仿真代码、debug 验证代码），大家可以进一步改进和拓展（支持边界约束、V 形标定板等）。

最后，这种标定相机和激光外参数的方法估计可以有效避开两个传感器之间的时间延时问题，因为两个传感器都是静止的，晃动标定板时每摆好一个 pose 稍微静止几十毫秒就能避免传感器延时的问题。

5. 参考文献

1. Qilong Zhang, Extrinsic Calibration of a Camera and Laser Range Finder (improves camera calibration)
2. On Closed-Form Formulas for the 3D Nearest Rotation Matrix Problem,
3. Finding the Nearest Orthonormal Matrix,
4. A Minimal Solution for the Extrinsic Calibration of a Camera and a Laser-Rangefinder
5. K.S. Arun, Least Squares Fitting of Two 3-d Point Set,
6. Automatic Extrinsic Calibration of a Camera and a 3D LiDAR using Line and Plane Correspondences
7. Wenbo Dong, A Novel Method for the Extrinsic Calibration of a 2D Laser Rangefinder and a Camera
8. B.T. Hinson,Observability-based guidance and sensor placement,

作者简介

贺一家，中科院自动化所博士毕业，目前为旷视研究院 SLAM 组研究员，研究方向为基于多传感器融合的 SLAM，结构化特征 SLAM 等。乐于分享和开源，对机器人、AR 等领域有浓厚兴趣。