VIO第六讲
Source
Edit
History

第六讲_三角化

Catalogue
  1. 1. 三角化
    1. 1.1. 相关代码

三角化

当估计出相机运动之后, 需要利用相机运动估计出特征点的空间位置，三角测量（三角化）就是用来解决这个问题的。三角化主要是单目mono使用

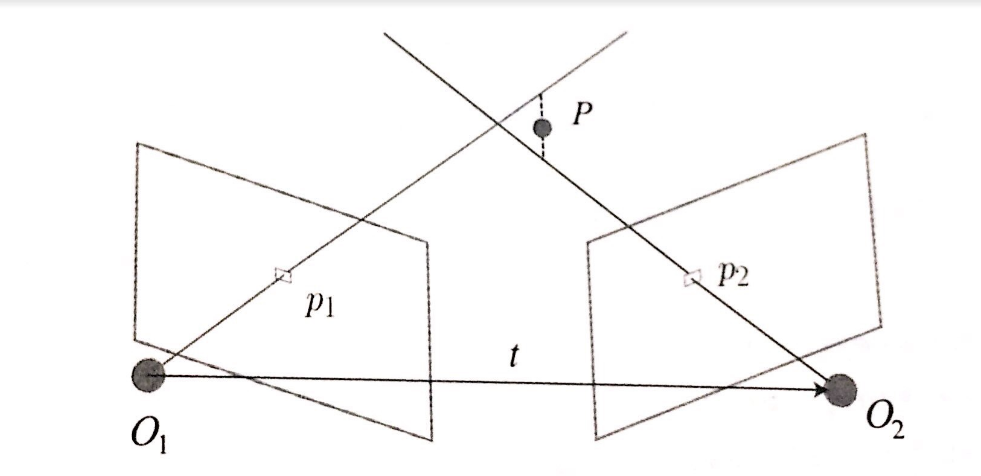
image-20200214160321348

问题描述：

​ 现在假设有两帧图像，其中两帧图像(Frame1,Frame2)的特征点匹配已有，相机的相对运动T_{21}(从第一帧到第二帧的变换)也已经获得，如何求解出某个特征点的空间坐标（以第一帧的相机坐标系为参考）？

假设：

  • 在第一帧坐标系下的某个路标点\(P\in R^4\)，(下式右侧)
  • 已知相机的位姿\(T_k=[R_k,t_k]\)，也就是第一帧坐标系转换到第二帧坐标系的变换矩阵\(T_{21}\)或者说是\(T_{CW}\)(如果第一帧是初始化帧的话)。
  • 利用相机的相对运动\(T_{21}\)(从第一帧到第二帧的变换)将路标点\(P\)投影到第二帧相机坐标系下，得到预测点的归一化平面坐标为\(p_2=x_k=[u_k,v_k,1]^T\)(下式左侧)

即： \[ \frac{1}{\lambda_k}x_k= \frac{1}{\lambda_k} \begin{bmatrix} u_k \\ v_k \\ 1 \end{bmatrix}_{1:3} =\bigg\{ T_k \begin{bmatrix} p_x \\ p_y \\ p_z \\ 1 \end{bmatrix}\bigg\}_{1:3} = \bigg\{ \begin{bmatrix} R_{k,3\times 3} & t_k \\ 0 & I \end{bmatrix} \begin{bmatrix} p_x \\ p_y \\ p_z \\ 1 \end{bmatrix} \bigg\}_{1:3} \] 其中，\(\lambda_k\)是逆深度，也就是\(\frac{1}{z_k}\)

问题是：如何求解上式右侧的第一帧坐标系下的某个路标点\(P\) ？

根据上式子的第三行，可以得到 \[ \frac{1}{\lambda_k}=T_{k,3}^T P= \begin{bmatrix} R_{k,3} & t_{k,3} \end{bmatrix}_{1\times4} \begin{bmatrix} p_x \\ p_y \\ p_z \\ 1 \end{bmatrix} \] 将（1）的前两行中的逆深度\(\frac{1}{\lambda_k}\)用上式等号右侧替换，得到 \[ T_{k,3}^T P u_k = T_{k,1}^T P \\ T_{k,3}^T P v_k = T_{k,2}^T P \] 于是，一帧就可以得到两个这样的方程，当有两帧或以上时，则：

\[ \begin{bmatrix} T_{1,3}^T u_1 - T_{1,1} \\ T_{1,3}^T v_1 - T_{1,2} \\ \vdots \\ T_{n,3}^T u_1 - T_{n,1} \\ T_{n,3}^T v_1 - T_{n,2} \\ \end{bmatrix} y = 0 \Longrightarrow Dy=0 \]

于是，把问题转化为求线性方程组的问题。

当观测次数>=2时，即有多帧观测到同一个路标点\(P\)，且这些帧对应的相机位姿已经知道的时候，由于各种测量噪声的影响，（投影回去的点并不是同一点），方程组的系数矩阵D很有可能满秩，（齐次线性方程组有唯一解），那么这个方程组就只有零解

于是，通常使用SVD分解来求这个方程组的最小二乘解 \[ \min_y || Dy ||_2^2 \] 其中， \[ ||y||=1 \] 求解方法：对\(D^TD\)进行SVD分解，得到 \[ \begin{aligned} D^TD &=U \Sigma V^T = \sum_{i=1}^{4} \sigma_{i}^2 u_i u_j^T \notag \\ &= \begin{bmatrix} u_{1,4 \times 1} & u_{2} & u_{3} & u_{4} \end{bmatrix}_{4 \times 4} \begin{bmatrix} \sigma_1^2 & 0 & 0 &0 \\ 0 & \sigma_2^2 & 0 & 0 \\ 0 & 0 & \sigma_3^2 & 0 \\ 0 & 0 & 0 & \sigma_4^2 \end{bmatrix} \begin{bmatrix} u_{1,4 \times 1}^T \\ u_{2}^T \\ u_{3}^T \\ u_{4}^T \end{bmatrix}_{4 \times 4} \end{aligned} \] 其中，\(u_1,u_2,u_3,u_4\)都是SVD分解产生的相互正交的单位向量，\(y\)也是单位向量

现在，回到要求解的问题上，即最小化目标函数： \[ \min_y ||Dy||_2^2=(Dy)^T(Dy)=y^TD^TDy \] \(y\)可以有\(D^TD\)分解之后的空间向量\(u_i\)经过线性组合得到，即 \[ y=\sum_{i}^4 k_i u_i= u_m+v \] 其中，\(u_m\)为任意的\(D^TD\)分解之后的空间向量\(u_i\)，另外\(v\)与\(u_m\)相互正交，即有： \[ v=\sum_{j,j\neq u}^4 k_j u_j \] 假设\(u_m=u_4\)，将\(y\)代入目标函数，得到 \[ \begin{aligned} \min_y ||Dy||_2^2 &=y^TD^TDy=(u_m+v)^T D^TD(u_m+v) \notag \\ &= [u_m+v]^T_{1 \times 4} ~ \begin{bmatrix} u_{1} & u_{2} & u_{3} & u_{4} \end{bmatrix}_{4 \times 4} \begin{bmatrix} \sigma_1^2 & 0 & 0 &0 \\ 0 & \sigma_2^2 & 0 & 0 \\ 0 & 0 & \sigma_3^2 & 0 \\ 0 & 0 & 0 & \sigma_4^2 \end{bmatrix} \begin{bmatrix} u_{1}^T \\ u_{2}^T \\ u_{3}^T \\ u_{4}^T \end{bmatrix}_{4 \times 4} [u_m+v]_{4 \times 1} \notag \\ &= \begin{bmatrix} v^Tu_1 & v^Tu_2 & v^Tu_3 & u_4^T u_4 \end{bmatrix} \begin{bmatrix} \sigma_1^2 & 0 & 0 &0 \\ 0 & \sigma_2^2 & 0 & 0 \\ 0 & 0 & \sigma_3^2 & 0 \\ 0 & 0 & 0 & \sigma_4^2 \end{bmatrix} \begin{bmatrix} u_1^Tv \\ u_2^Tv \\ u_3^Tv \\ u_4^Tu_4 \end{bmatrix} \notag \\ &= \sigma_1^2v^Tu_1u_1^Tv+ \sigma_2^2v^Tu_2u_2^Tv+ \sigma_3^2v^Tu_3u_3^Tv+ \sigma_4^2u_4^Tu_4u_4^Tu_4 \notag \\ &= (\sigma_1^2+\sigma_2^2+\sigma_3^2)v^Tv+\sigma_4^2 \end{aligned} \] 同理，当\(u_m=u_1\)时 \[ y^TD^TDy=(\sigma_4^2+\sigma_2^2+\sigma_3^2)v^Tv+\sigma_1^2 \] 当\(u_m=u_2\)时 \[ y^TD^TDy=(\sigma_1^2+\sigma_4^2+\sigma_3^2)v^Tv+\sigma_2^2 \] 当\(u_m=u_3\)时 \[ y^TD^TDy=(\sigma_1^2+\sigma_2^2+\sigma_4^2)v^Tv+\sigma_3^2 \]

当且仅当\(u_m=u_4\)且\(v=0\)时，目标函数\(y^TD^TDy\)取最小值\(\sigma_4^2\)

综上，当\(y\)等于奇异值向量\(u_4\)时，为最小二乘解。

  • 另外，\(y\)是单位向量，需要进行scale把z值恢复到相机坐标系z=1的归一化平面，此时即可得到对应的坐标P
  • 或者, 如果需要恢复完整的点P而不是归一化到z=1平面上的点, 那么可以进行scale, 对\(y\)向量的齐次化维, 即第4维进行归一化, 即可得到真正的点P

\[ P= \frac{y_{1:4}}{y[4]} = \begin{bmatrix} y_1/y_4 \\ y_2/y_4 \\ y_3/y_4 \\ y_4/y_4 \end{bmatrix} = \begin{bmatrix} P_x \\ P_y \\ P_z \\ 1 \end{bmatrix} \]

相关代码

代码之前, 有一些细节需要注意:

  • 结论: \(\color{red}{t_{cw} \neq -t_{wc}}\) , 之间还差了一个旋转变换
  • 若已知从相机坐标系到世界坐标系的变换\(T_{wc}=[R_{wc},t_{wc}]\) 则有相机坐标系的点转换到世界坐标系的转换\(P_{w}=R_{wc}P_c + t_{wc}\)
  • 那么从世界坐标系到相机坐标系的变换\(T_{cw}=[R_{cw} , t_{cw}]=[R_{wc}^T,-R_{wc}^T t_{wc}]\) , 原因是, 根据上面"相机坐标系到世界坐标系的转换 ", 反推出世界坐标系到相机坐标系的转换 \(P_{c}=R_{wc}^{-1}( P_w - t_{wc})=R_{cw}( P_w - t_{wc})\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
//
// Created by hyj on 18-11-11.
//
#include <iostream>
#include <vector>
#include <random>  
#include <Eigen/Core>
#include <Eigen/Geometry>
#include <Eigen/Eigenvalues>
#include <Eigen/Jacobi>
#include <Eigen/SVD>

struct Pose
{
    Pose(Eigen::Matrix3d R, Eigen::Vector3d t):Rwc(R),qwc(R),twc(t) {};
    Eigen::Matrix3d Rwc;
    Eigen::Quaterniond qwc;
    Eigen::Vector3d twc;

    Eigen::Vector2d uv;    // 这帧图像观测到的特征坐标
};
int main()
{

    int poseNums = 10;
    double radius = 8;
    double fx = 1.;
    double fy = 1.;
    std::vector<Pose> camera_pose;
    for(int n = 0; n < poseNums; ++n ) {
        double theta = n * 2 * M_PI / ( poseNums * 4); // 1/4 圆弧
        // 绕 z轴 旋转
        Eigen::Matrix3d R;
        R = Eigen::AngleAxisd(theta, Eigen::Vector3d::UnitZ());
        Eigen::Vector3d t = Eigen::Vector3d(radius * cos(theta) - radius, radius * sin(theta), 1 * sin(2 * theta));
        camera_pose.push_back(Pose(R,t));
    }

    // 随机数生成 1 个 三维特征点
    std::default_random_engine generator;
    std::uniform_real_distribution<double> xy_rand(-4, 4.0);
    std::uniform_real_distribution<double> z_rand(8., 10.);
    double tx = xy_rand(generator);
    double ty = xy_rand(generator);
    double tz = z_rand(generator);

    Eigen::Vector3d Pw(tx, ty, tz);
    // 这个特征从第三帧相机开始被观测，i=3
    int start_frame_id = 3;
    int end_frame_id = poseNums;
    for (int i = start_frame_id; i < end_frame_id; ++i) {
        Eigen::Matrix3d Rcw = camera_pose[i].Rwc.transpose();
        //注意这里,
        // pose结构体里面关于相机位姿它这里并不是world->camera, 而是camera->world
        // 而实际的投影应该是 Pc= Rcw*Pw + tcw
        // 但是仅有的参数只有 Rwc 和 twc
        // 从等式 Pw= Rwc*Pc + twc
        // 可以得到 Pc= Rcw*Pc + tcw = Rwc*Pc -Rwc*twc
        // 所以,从世界坐标系到相机坐标系的平移量 tcw= -Rwc*twc
        Eigen::Vector3d Pc = Rcw * (Pw - camera_pose[i].twc);

        double x = Pc.x();
        double y = Pc.y();
        double z = Pc.z();

        camera_pose[i].uv = Eigen::Vector2d(x/z,y/z);
    }
    
    /// TODO::homework; 请完成三角化估计深度的代码
    // 遍历所有的观测数据，并三角化
    Eigen::Vector3d P_est;           // 结果保存到这个变量
    P_est.setZero();
    /* your code begin */
    //构造系数矩阵D
    Eigen::MatrixXd D(2*(camera_pose.size()-start_frame_id),4);
    for (int i=start_frame_id;i<camera_pose.size();i++) {
        Eigen::Isometry3d T_i=Eigen::Isometry3d::Identity();
        T_i.rotate(camera_pose[i].Rwc.transpose());
        //从世界坐标系到相机坐标系的平移量 tcw= -Rwc*twc
        T_i.pretranslate(-camera_pose[i].Rwc.transpose()*camera_pose[i].twc);

        D.row(2*(i-start_frame_id))=T_i.matrix().row(2)*camera_pose[i].uv[0]-T_i.matrix().row(0);
        D.row(2*(i-start_frame_id)+1)=T_i.matrix().row(2)*camera_pose[i].uv[1]-T_i.matrix().row(1);
    }
    std::cout<<D<<std::endl;
    //对D^TD进行SVD分解
    Eigen::JacobiSVD<Eigen::MatrixXd> svd(D.transpose()*D, Eigen::ComputeThinU | Eigen::ComputeThinV);
    Eigen:: MatrixXd U = svd.matrixU();
    Eigen:: MatrixXd V = svd.matrixV();
    Eigen:: MatrixXd A = svd.singularValues();

    P_est=U.col(3).head(3);
    //std::cout<<U.col(3).norm()<<std::endl;
    P_est /= U.col(3)[3];

    Eigen:: VectorXd b(2*(camera_pose.size()-start_frame_id));
    b.setZero();

    Eigen::Vector4d result;
    result=D.jacobiSvd(Eigen::ComputeThinU | Eigen::ComputeThinV).solve(b);
    std::cout<<result.transpose()<<std::endl;

    /* your code end */
    
    std::cout <<"ground truth: \n"<< Pw.transpose() <<std::endl;
    std::cout <<"your result: \n"<< P_est.transpose() <<std::endl;
    return 0;
}