第五讲(上)_最小二乘求解器Solver流程&代码
非线性最小二乘
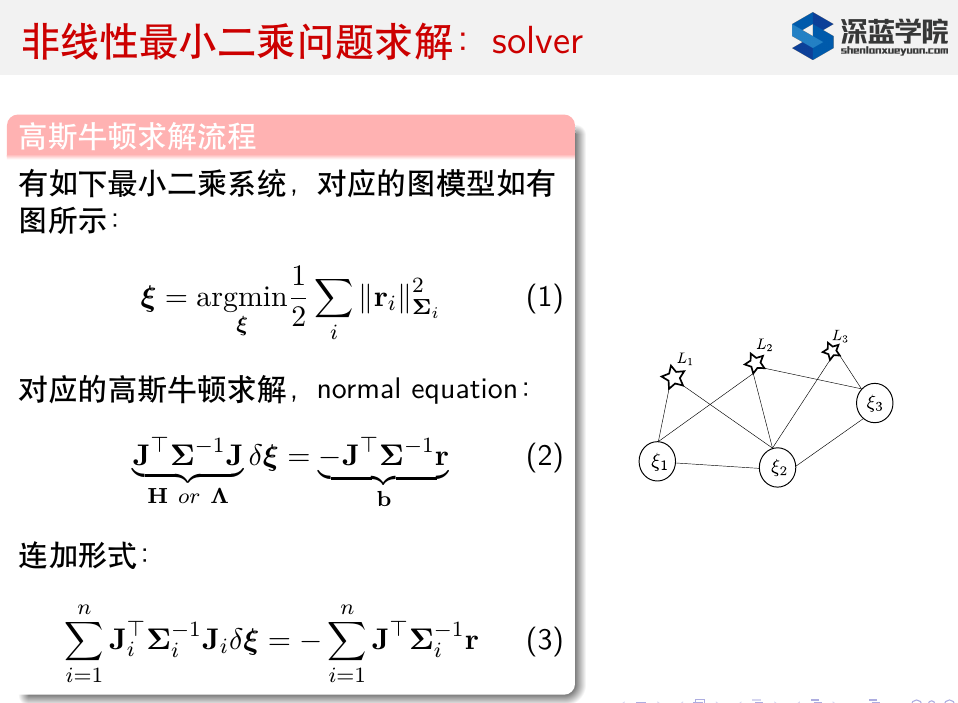
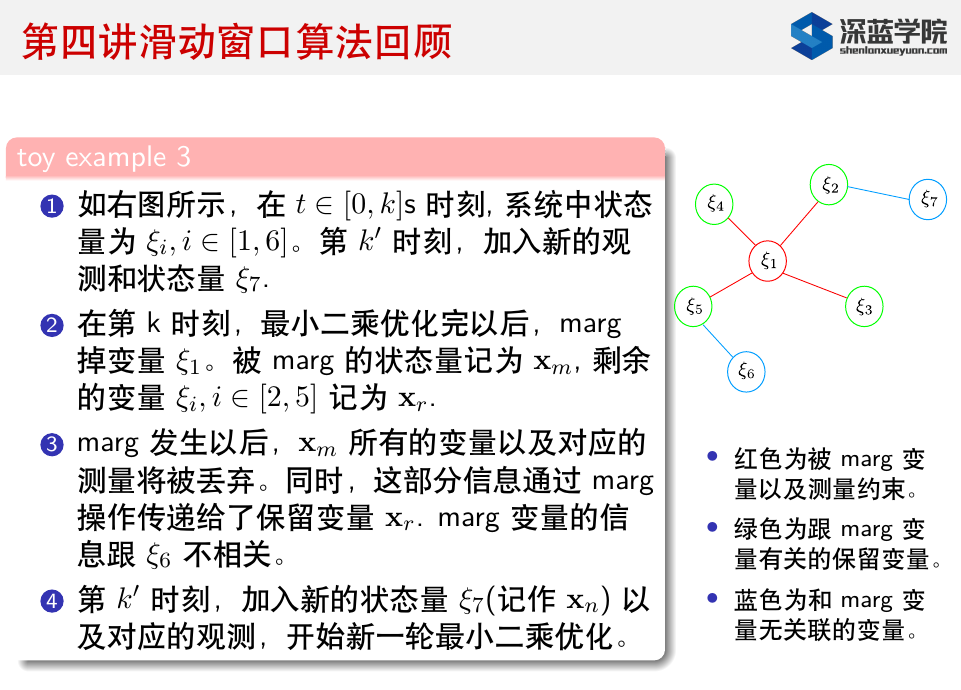
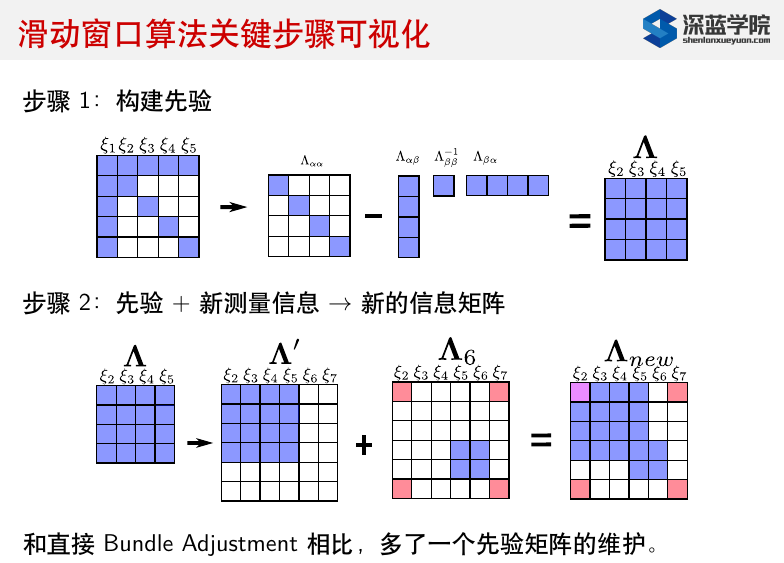
- 关于舒尔补操作消元,可参考<视觉SLAM14讲的BA部分>

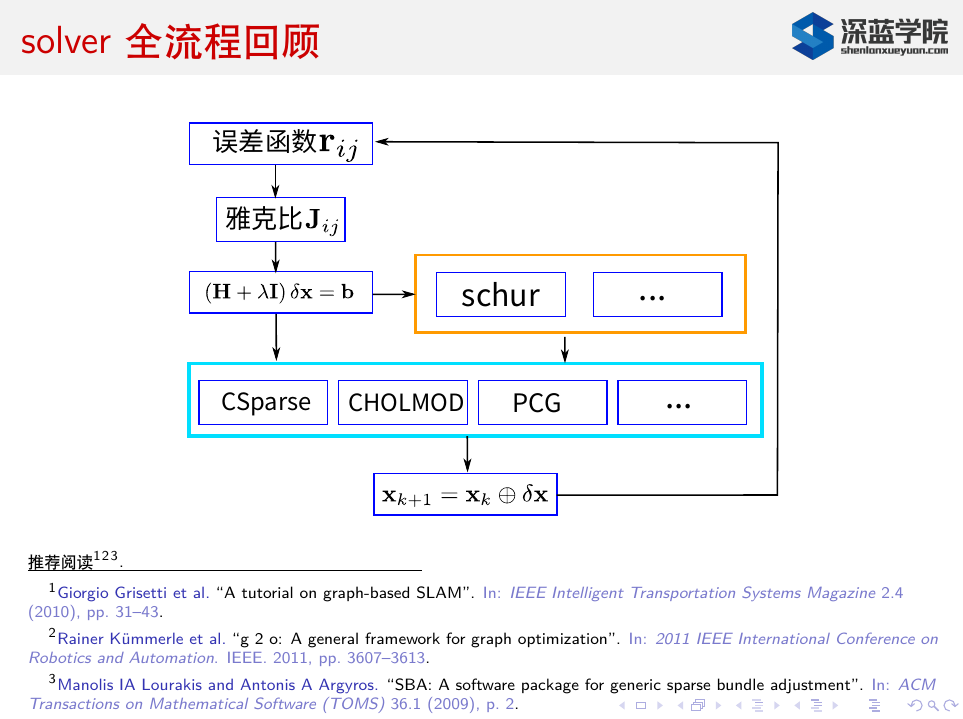
求解过程的细节操作

解释:
- 使用LM算法可以强行使得信息矩阵H满秩, 但是有可能造成整条轨迹相对世界坐标系发生漂移, 尽管整条轨迹的残差已经达到最小值, 也就是所说的零空间变化. 举例: 对整条轨迹的漂移问题, 可以对整条轨迹乘以一个变换矩阵\(T\), 使轨迹变换到原来的状态.
- 固定某个位姿顶点\(\xi_i\), 通常是固定第0个姿态\(\xi_0\)为(0,0,0,0,0,0), 这相当于人为的给整条轨迹BA的信息矩阵添加先验信息(添加了额外的观测), 使得原本不是满秩的信息矩阵H变成满秩.
- 针对尺度不可观的问题, 可采取 (1)对某个固定之后的位姿\(\xi_i\)所能观测到的某个路标点\(L_i\)也进行固定, 使得整个BA的尺度固定下来. (2)对连续两个位姿\(\xi_i\)和\(\xi_{i+1}\)进行固定, 使得轨迹的尺度确定下来.
- 具体操作:
- g2o论文: 对第一个位姿\(\xi_1\)对应的信息矩阵加上单位阵I, 使得位姿\(\xi_1\)对应的增量\(\delta x_1\)被强行约束为0. \[ \begin{aligned} \begin{bmatrix} H_{11}+I\\ H_{12} \\ \vdots \end{bmatrix} \Delta X = b \\ \Longrightarrow \delta x_1 = 0 \end{aligned} \]
- 添加超强先验: 直接把位姿\(\xi_1\)对应的信息矩阵设置为无穷大, 使得\(\delta x_1\)无限接近0
- g2o实现: 把位姿\(\xi_1\)对应的雅克比设置为0, 直观上意味着残差=0, 残差=0, 意味着不用优化该位姿, \(\delta x_1\)=0.
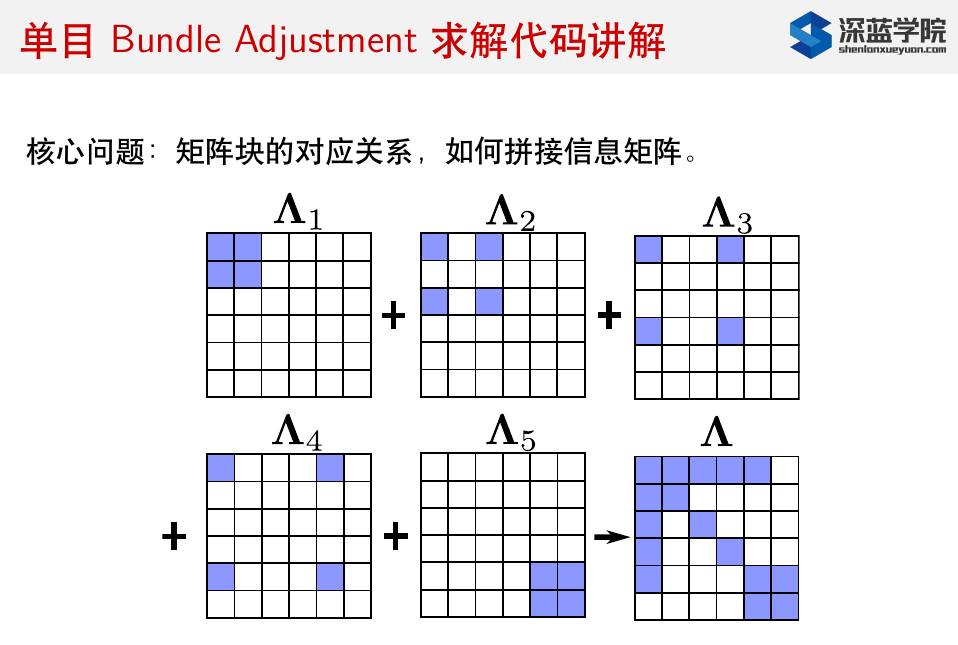

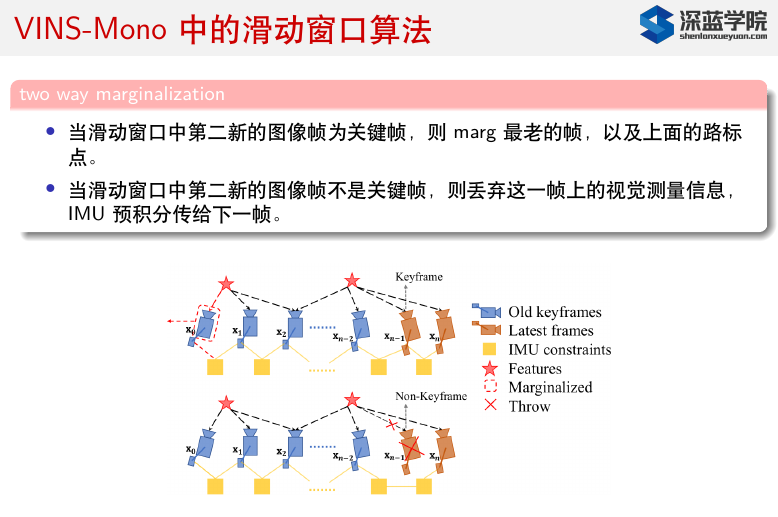
第五讲(下)_滑动窗口