Catalogue
1. ORB_SLAM2

2. 预备知识【1】

2.1. ICP SE3/Sim3求解
2.1.1. 已知n对匹配的3D点----3点法求R

- 这3个点实际上是世界坐标系W中的点,即世界坐标系中的点\(p_1,p_2,p_3\)构造出一个新的坐标系O,其中\(p_1\)的意义就相当于相机的坐标
- 根据这3个点\(p_1,p_2,p_3\),可以得到坐标系O的三个轴的方向在世界坐标系W的表示
- 根据坐标系O的三个轴的方向在世界坐标系W的表示,可以写出从世界坐标系W到坐标系O的旋转变换\(R_{w2o}=[\bar{x},\bar{y},\bar{z}]\),(我自己而言还是比较习惯写成\(R_{o\leftarrow w}=[\bar{x},\bar{y},\bar{z}]\)的形式)
- 如果知道两组这样的的点,并且这两组点一一匹配
- 那么就可以写出这从上面坐标系O到下面坐标系O'的旋转变换\(R_{o2o'}=R_{w2o'}R_{w2o}^T\),(我自己而言还是比较习惯写成\(R_{o'\leftarrow o}=R_{o'\leftarrow w}R_{o\leftarrow w}^T\)的形式)
当匹配对数n>3,则可以采用最小二乘的方法,最小化误差
2.1.2. 求Sim3尺度因子

- 上图中,\(p_i'=p_i-p^-\),\(q_i'=q_i-q^-\)
2.1.2.1. 尺度因子的正解:

2.1.3. 求旋转R的四元数方法

2.2. 3D-2D PnP

2.2.1. EPnP

需要4个点是因为原点+3个方向
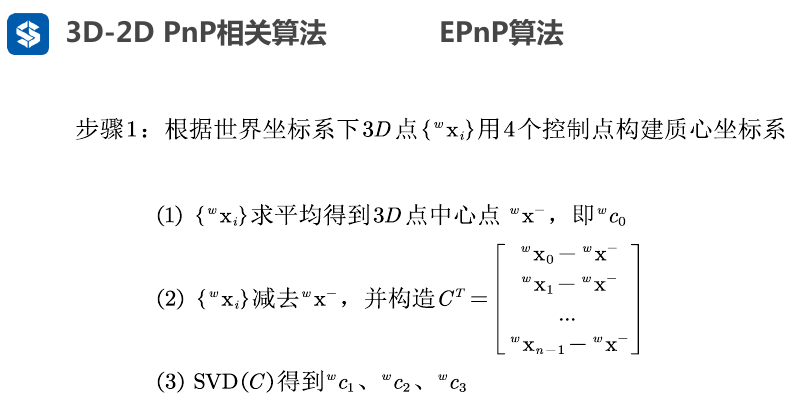
得到4个控制点分别是c0, c1, c2, c3 模长均为1

世界坐标系下的每个点\(x_i^w\)都可以用4个控制点以及映射关系\([\alpha_1,\alpha_2,\alpha_3,\alpha_4]^T\)来表示
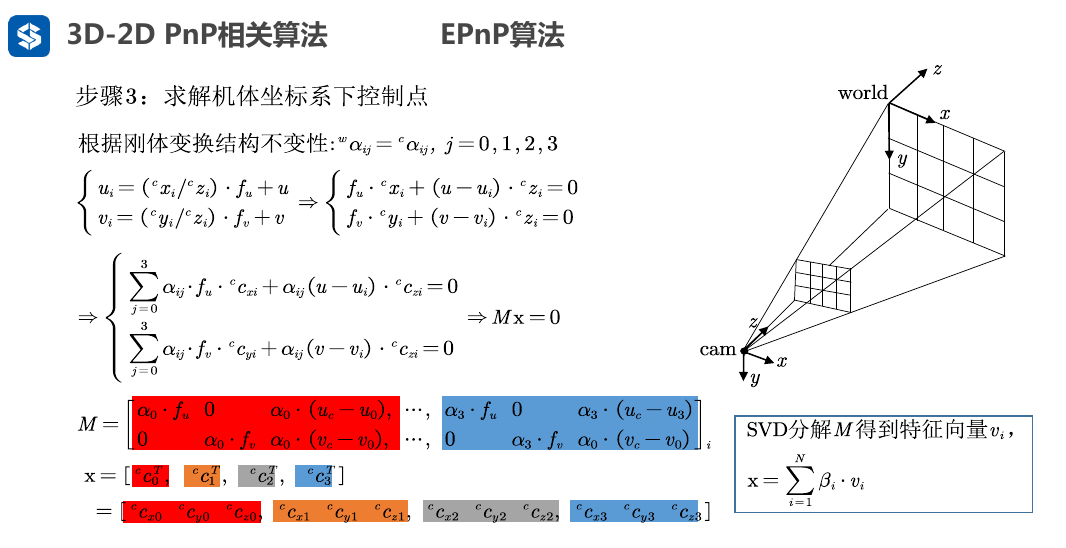
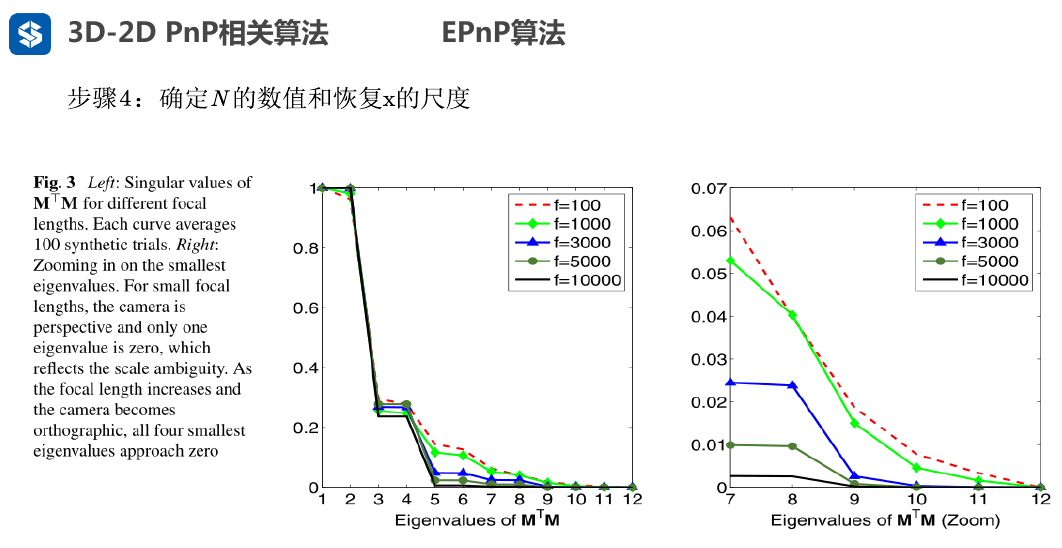

EPNP 省略一部分
2.2.2. DLT算法

2.3. 2D-3D 三角化
2.3.1. 单目
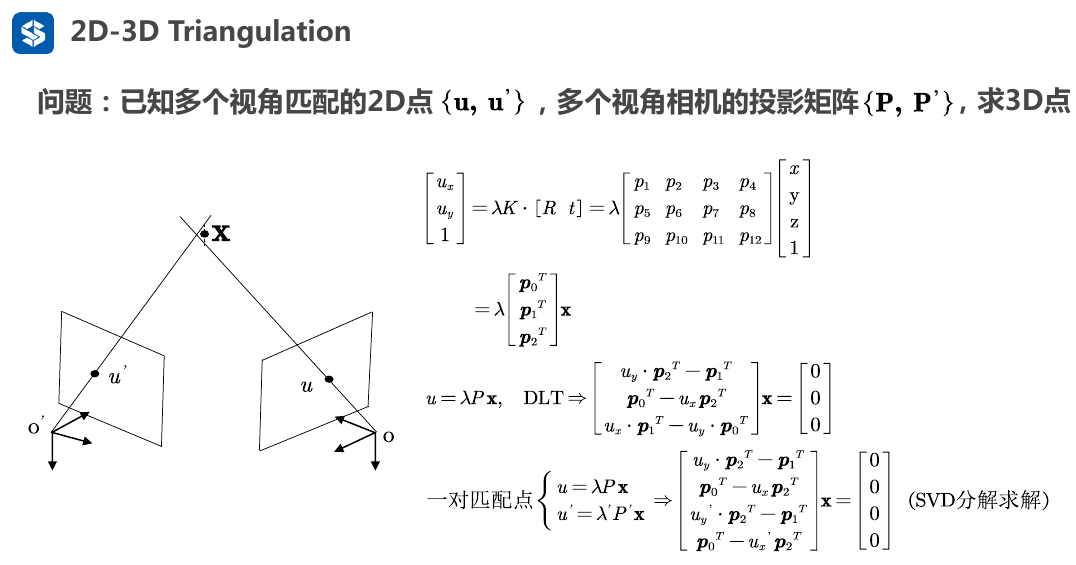
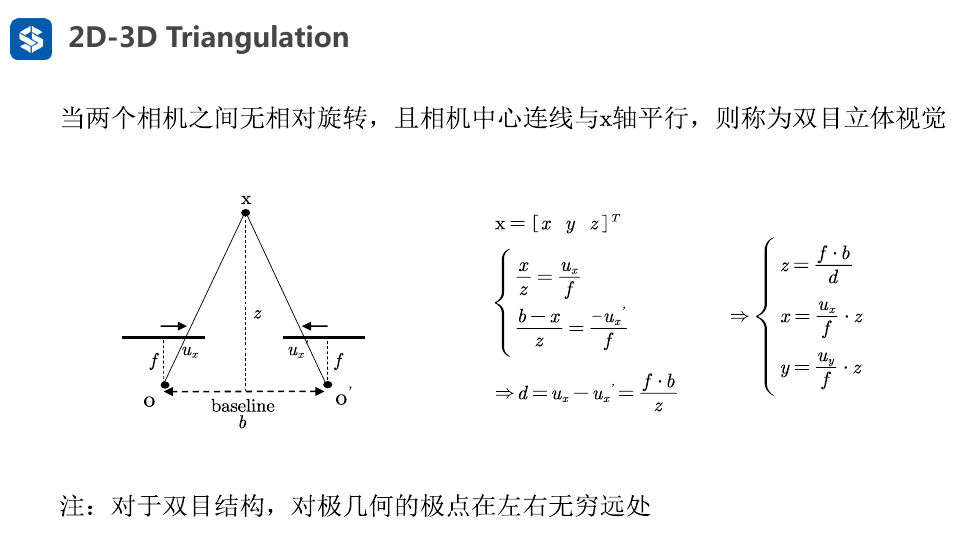
2.3.2. 双目立体
2.4. 2D-2D Homography/Fundamental 对极几何
2.4.1. 基础矩阵与本质矩阵
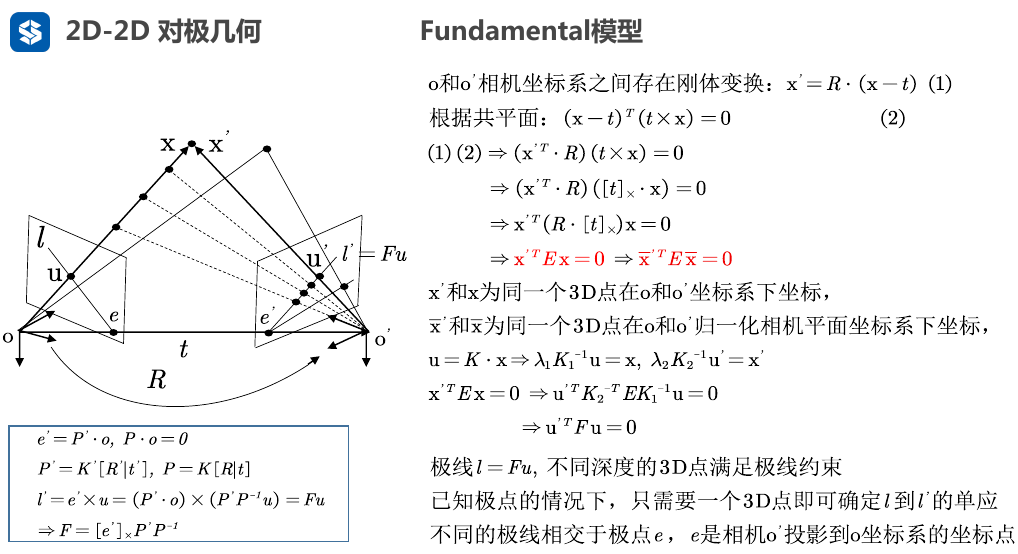
- 极线\(l'=e' \times u\) 的意思是, 这里的 极线 \(l'\) 指的是这条极线在相机平面上的法向量
- 换句话说, 相机平面上极线上的两个点叉乘, 即向量叉乘\(e' \times u\) , 得到极线所在平面上的法向量\((a,b,c)\)
- 这个法向量可以构成极线点法式方程, 设极点\(e(e_x,e_y,1)\) , 那么极线方程为 \(ae_x+be_y+c=0\)
- 利用这个法向量, 可以出点\(p_{proj}=[p_x,p_y,1]^T\)到这条直线的距离 \(d=\frac{|ae_x+be_y+c|}{\sqrt{a^2+b^2}}=\frac{l'*p_{proj}}{\sqrt{a^2+b^2}}\)
- 因此, 这个距离也就是极线约束, 利用这个距离可以判断基础矩阵F的好坏 (ORB_SLAM2 Initializer::CheckFundamental()函数就是这么计算初始化的基础矩阵F得分 )
e'和u不是指二维像素点坐标(u,v),二维没法做叉乘, e'应该指的是相机坐标系O'到像素点e'的向量,u类比,这样才能做叉乘,叉乘完之后得到的是极线l'在平面上的法向量,这个法向量用来计算投影点到极线的距离。(点法式方程)

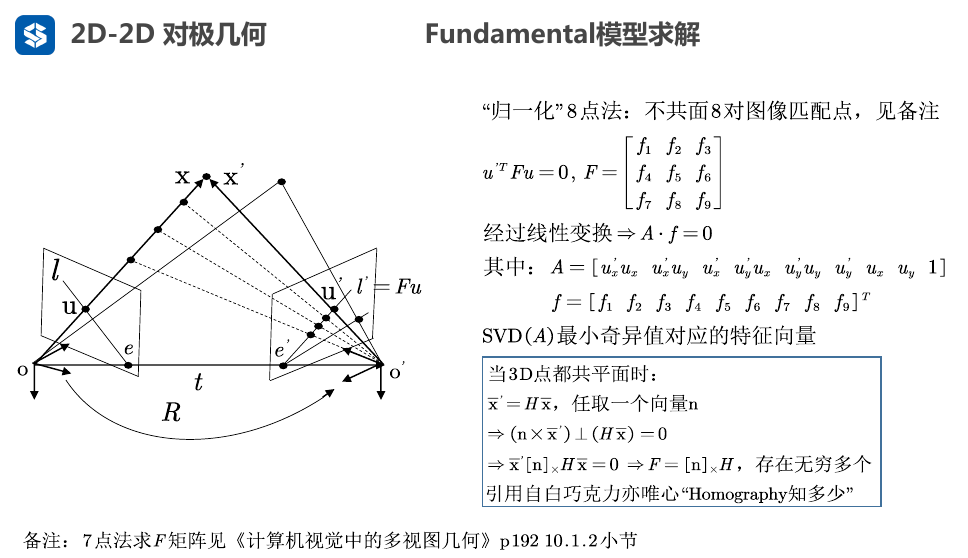
注意 8点法的8个点不能在同一个平面上, 如墙壁
原因是3D点共面时, 就满足单应性\(\bar{x}'=H\bar{x}\)
后话: 所以, 一般操作时都会计算F和H, 两种情况, 看哪种情况下更好
另外: H矩阵的筛选点能力要强一些( 去除outlier ? )
另外: 纯旋转不能用求F

- 由基础矩阵约束 \(u_2^T*F*u_1=0\)
- 可以得到,使用归一化的点代入,有: \(\bar{u}_2^T \bar{F} \bar{u}_1'=0\)
- 因此,使用归一化的点代入约束方程,可以求出\(\bar{F}\)
- 又因为\(\bar{u}_2'=T_2 u_2 , \bar{u}_1'=T_1 u_1\)
- \(\bar{u}_2^T \bar{F} \bar{u}_1' = (T_2 u_2)^T \bar{F} (T_1 u_1) = u_2^T(T_2^T \bar{F} * T_1)* u_1 = 0\)
- 所以,最终要求归一化之前的F
- \(u_2^T(T_2^T \bar{F} * T_1)* u_1=u_2^T*F*u_1=0\)
- \(F=T_2^T \bar{F} * T_1\)
ORB_SLAM2中归一化变换代码
1 | void Initializer::Normalize(const vector<cv::KeyPoint> &vKeys, vector<cv::Point2f> &vNormalizedPoints, cv::Mat &T) |

ORB_SLAM2中计算基础矩阵F的代码(8点法)
1 | void Initializer::FindFundamental(vector<bool> &vbMatchesInliers, float &score, cv::Mat &F21) |
ORB_SLAM2中利用基础矩阵F约束进行重投影的代码
1 | //利用基础矩阵F进行重投影,计算得分 [理解对极约束] |
ORB_SLAM2中分解基础矩阵F得到R,t 代码
1 | bool Initializer::ReconstructF(vector<bool> &vbMatchesInliers, cv::Mat &F21, cv::Mat &K, |
2.4.2. Homography模型
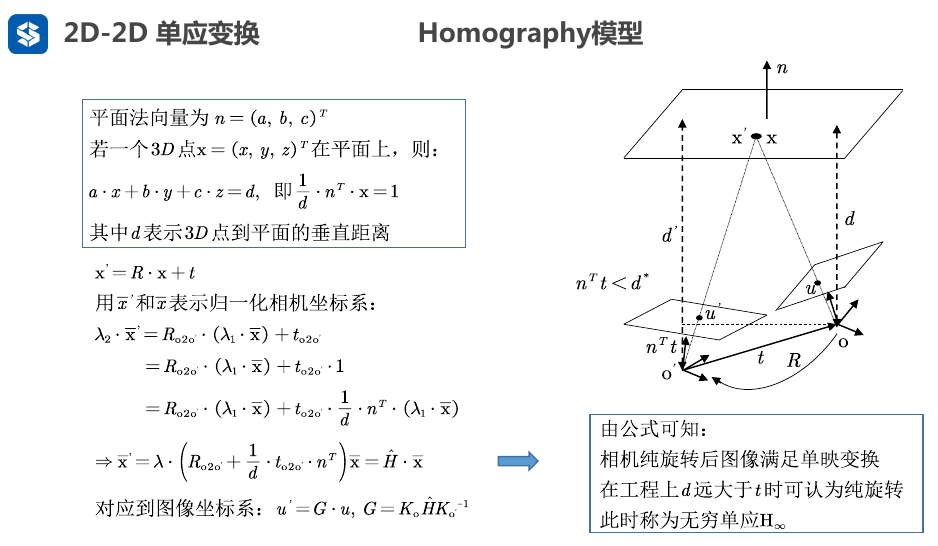
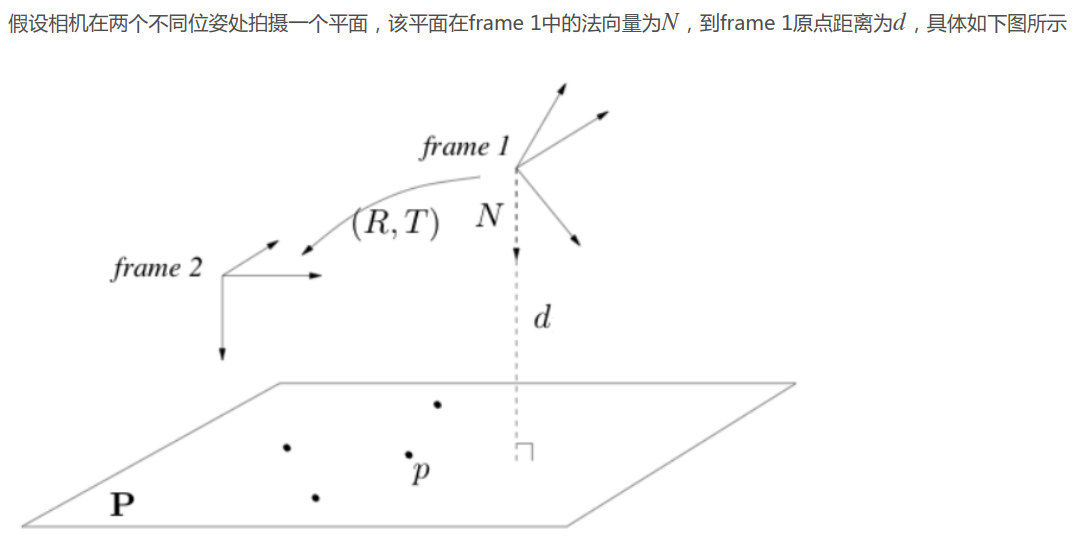
- \(d\)表示的是平面到相机坐标系原点O的距离, 上面的"其中d表示~"说法有误。
下面给出"白巧克力亦违心"的博客内容:

- 注意: 上面的单应矩阵\(\hat{H}\)是包含了尺度项\(\lambda\), 所以\(\hat{H}=\lambda H\) , 可以把h9看做是包含了\(\lambda\)的项, 所以, 这里(ORB_SLAM2)的 H 矩阵参数为9个
- 这里 \(Ah=0\) 与<视觉SLAM14讲-第二版 P171 公式7.20>的两个约束是对应的, 不同的地方是这里没有把h9看做是1, 这里的h9包含\(\lambda\)项, 把它看做参数一起求了.

ORB_SLAM2计算单应矩阵H代码
1 | void Initializer::FindHomography(vector<bool> &vbMatchesInliers, float &score, cv::Mat &H21) |
ORB_SLAM2利用单应矩阵H进行重投影约束代码
1 | //通过单应矩阵H21以及H21_inv 反投影,计算误差,得到当前单应矩阵H的分数 |
2.4.3. 2D-2D模型约束与外点剔除

下面是分解的方法推导, 可暂时不看
Faugeras SVD 解法求R,t

- 对右侧得到的3个方程(2) (3) (4) 两两之间乘以\(t^{'}\)的系数, 例如将方程(2)乘以\(x_2\) , 将方程(3)乘以\(x_1\), 两式相减, 可以得到一个消去\(t^{'}\)的方程, 两两操作, 一共得到三个新的方程如下
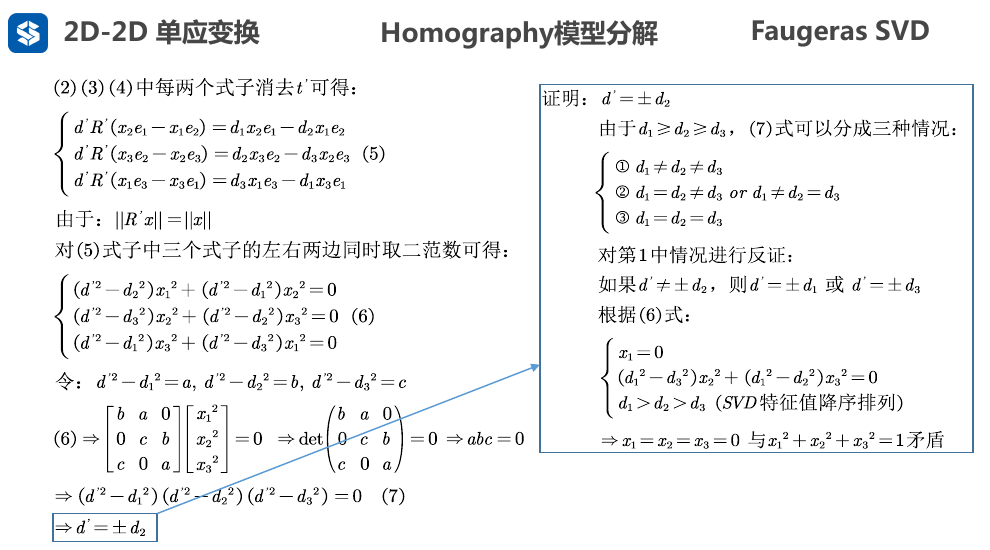
- 技巧1: 利用旋转变换不改变向量模长的性质, 可以对等式两边同时取范数, 即可消去旋转矩阵\(R\)
- 技巧2: 根据克莱姆法则,系数行列式delta不等于0时, 线性方程组只有唯一零解。因此, 要使齐次线性方程组有非零解, 则系数矩阵的行列式要等于0 . 性质用于上面的方程(6)
- 证明中: 由于\([x_1,x_2,x_3]^T\)是法向量\(n^{'}\), 所以 模长不可能为0
- 最后得到距离\(d^{'}\)等于特征值\(d_2\)

- 先求R' , 再求t'
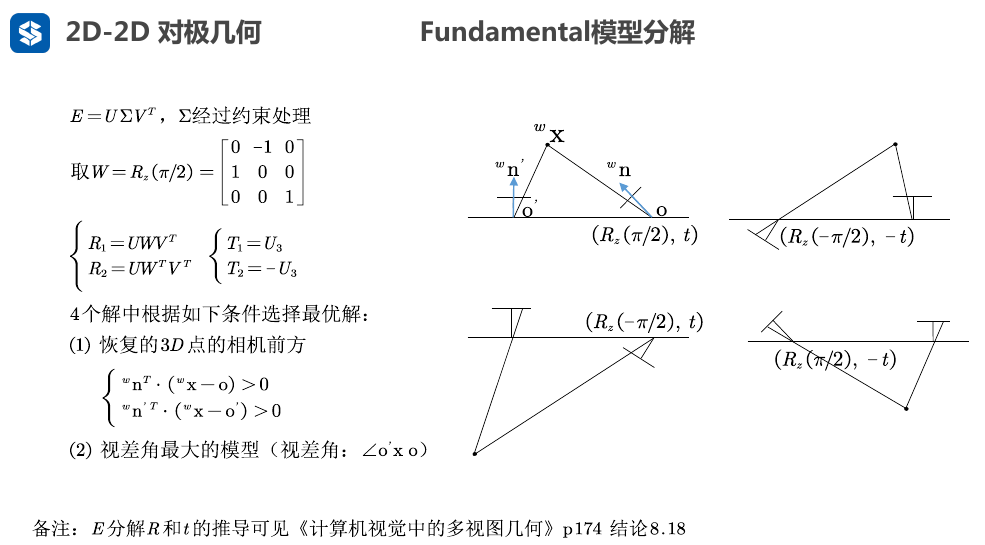
- 最后由约束\(n^T t <d\) (两个相机位姿平移量远小于相机坐标系原点到3D点平面的距离) , 来使得3D点均在相机同一面, 剩下4种符合的情况
- 然后实际上又可以通过判断3D点(路标点) 是否在相机的正前方, 以及视差角, 在正前方的点 这些数据来筛选出最终的R,t

- 由于\(d'\) 可以为\(+d_2\)或者\(-d_2\) , 每种情况下又有4种符合, 所以一共得到8种情况 (8种情况下3D点都在两个相机位姿的同一面)
- 对这8种情况进行筛选, 选出3D点在相机正前方的情况
- 最后再选取最符合实际情况(比如正前方3D点最多的)一种作为最终的解 , 求出 $R' , t' $
Malis 解法求R,t

- 关于左侧\(det(\hat H^T \hat H -\lambda I)=0\) 也没说清楚, 貌似不太严谨? opencv是这么做了
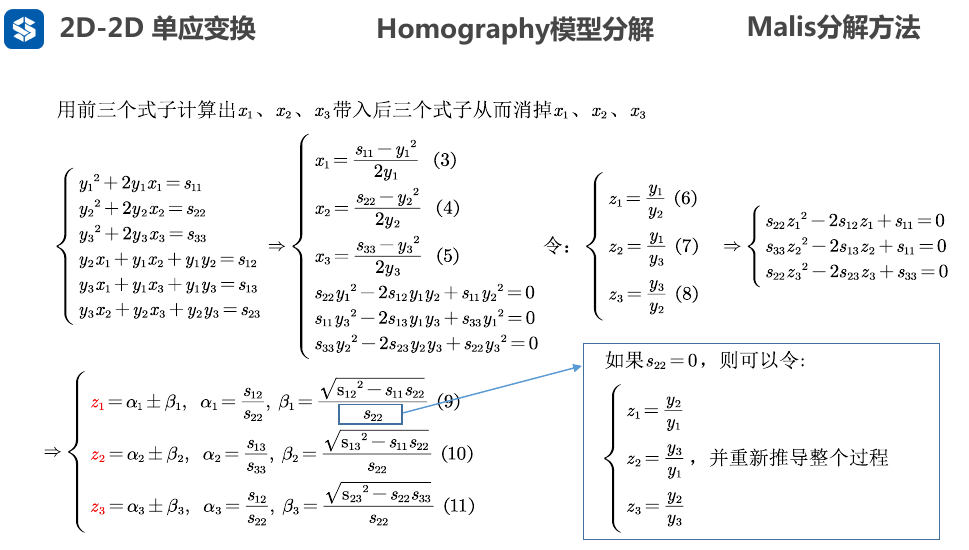
- 这里还不能求出\(y_1 , y_2 , y_3\), 只能求出\(z_1, z_2, z_3\)
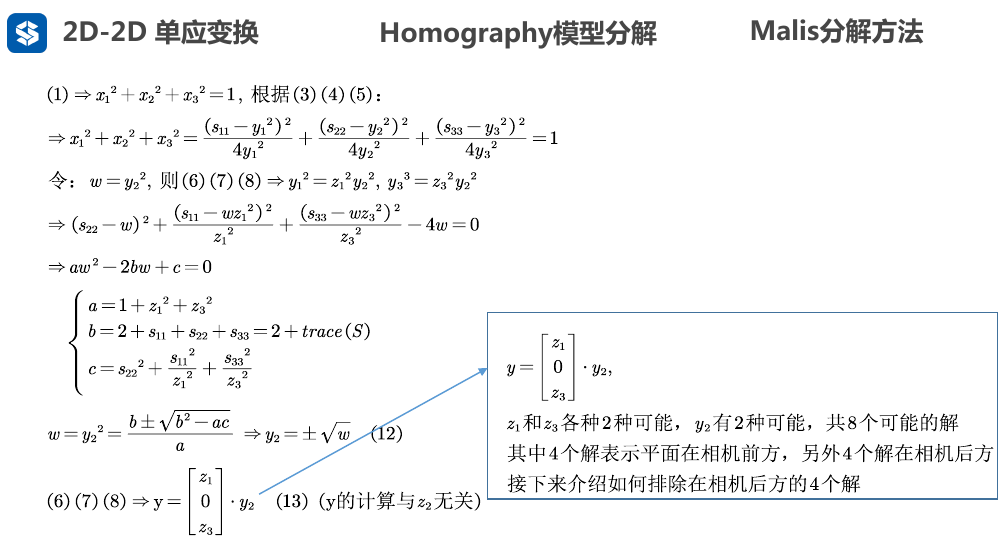
- 因为前面令\(x=\frac{R^T t}{|| R^T t||}=[x_1,x_2,x_3]^T\) , 显然 \(x\)是单位向量,而且 旋转矩阵R 不改变向量模长, 因此 可以得到\(x_1^2+x_2^2+x_3^2=1\)



Zhang SVD 解法求R,t

求齐次方程组最小二乘解-SVD