1. Real-Time Loop Closure in 2D LIDAR SLAM

2. 摘要
提出的方法应用在一个小型背包平台,可以达到实时的建图和定位,回环精度为5CM。为了达到实时的回环检测,使用了分枝定界为帧扫描和子图的匹配运算进行加速,这个方法达到了state-of-art。
3. 介绍
相反,本文的贡献在于提出了一种新的方法来降低从激光数据计算回环约束的计算要求,这种技术使SLAM能够绘制非常大的楼层,数万平方米的面积,同时实时为操作员提供完全优化的结果。
4. 相关工作
4.1. Scan-to-scan matching
常用于计算相对位姿的变化,具有累计误差。
4.2. Scan-to-map matching
有助于限制累计误差,其中一种方法是使用高斯-牛顿法在线性插值的地图上找到局部最优解。在这种情况下,通过使用足够高的数据率激光雷达提供良好的姿态初始估计,局部优化的扫描到地图匹配是有效和稳健的,在不稳定平台上,可以利用惯性测量单元(IMU)估计重力方向。
4.3. Pixel-accurate scan matching
可进一步减少局部累计误差,尽管需要更进一步的计算力,但是这个方法对于回环检测十分有用。一些方法侧重于通过匹配从激光扫描中提取的特征来提高计算cost,其他方法还有使用基于直方图匹配的,基于扫描特征提取的,还有使用机器学习的。
4.4. Else
处理剩余的局部误差积累的两种常用方法是粒子滤波和基于图的方法
4.5. 粒子滤波
粒子滤波器必须在每个粒子中维护一个完整系统状态的表示,对于基于网格的SLAM,随着地图变大,这很快就会成为资源密集型系统。
4.6. 图优化
基于图的方法在一组表示姿态和特征的节点上工作,图中的边是由观察产生的约束,可以使用各种优化方法来最小化所有约束带来的误差。
5. 系统概述
谷歌的Cartographer提供了一个实时的室内测绘解决方案,它采用了一个配备传感器的背包,可以生成分辨率为r = 5厘米的2D网格地图,该系统的操作员可以在穿过建筑物时看到正在创建的地图。
激光扫描被插入到子图上的一个最优位姿,在短时间内具有足够的准确度。扫描匹配是针对最近的子图进行的,因此它只依赖于最近的扫描,并且世界帧中的姿态估计的误差会累积。
为了解决积累的误差,我们定期运行一个位姿优化。当一个子图完成,就不会再新的一帧被插入,这个子图将会成为回环检测的一部分。所有完成的子图和激光扫描都被自动的被考虑到回环检测中。如果它们(激光扫描和子图之间)根据当前的位姿估计足够接近,则扫描匹配器尝试在子图中找到对应的激光扫描。
如果在当前估计位姿附近所创建的搜索窗口中找到了足够好的匹配,将会增加一条回环约束到最优化问题中。通过每几秒计算一次优化问题,可以看到,每当重新回到某个已经到达过的位置时,将会立即得到回环约束。
6. 局部2D-SLAM
系统结合了分离的局部和全局的方法来实现2D-SLAM。每一种方法的目的都是取优化位姿\(\xi\),\(\xi=(\xi_x,\xi_y,\xi_\theta)\)由平移量\((x,y)\)和旋转量\(\xi_\theta\)组成。对于激光雷达的观测,基本上就是一帧的激光扫描。在一个不稳定的平台上,比如我们的背包,一个IMU被用来估计重力的方向,从水平安装的激光雷达投射扫描到2D世界。
在我们的局部方法中,每个连续的扫描都是针对世界的一小块区域进行匹配的,称为子图\(M\),使用了非线性优化的方法将一帧扫描和当前子图对齐,这个过程进一步称为扫描匹配。扫描匹配会随着时间积累错误,稍后通过全局方法消除这些错误。
6.1. Scans
子图的构造是对扫描和子图坐标系进行多次对齐的迭代过程,又称帧。基于一帧扫描的坐标原点,可以写出所有激光点\(H=\{h_k\}_{k=1,\cdots,K},h_k \in R^2\)。这一帧的扫描在子图坐标系的位姿\(\xi\)可以使用变换\(T_{\xi}\)来表示,即如下的变换:
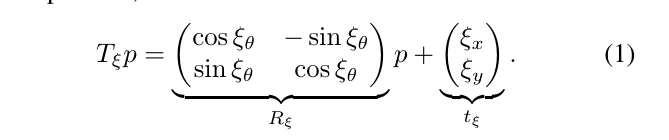
6.2. Submaps
一些连续的激光扫描用于构建一个子图,这些子图具有概率网格的形式\(M:rZ \times rZ \rightarrow [p_{min},p_{max}]\),这些离散网格具有分别率,如5cm一个网格点。每一个网格所对应的值可以看做是该网格被占据的概率。对于每一个网格点,定义相应的像素,使该像素由最接近网格点的所有点组成。
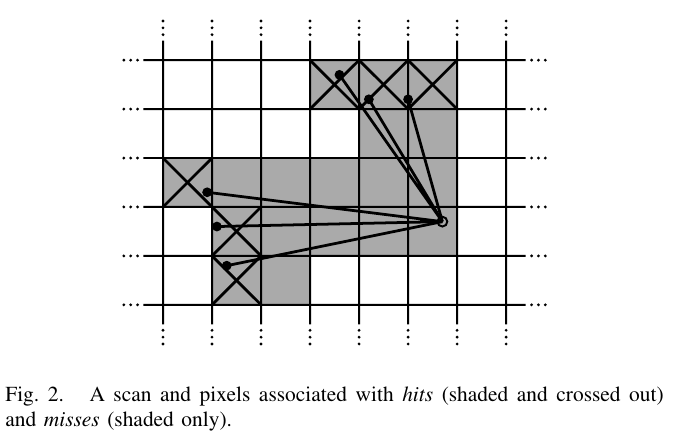
当一帧扫描被插入到概率网格,将计算网格点的\(hits\)和\(misses\)。对于每一次命中,我们都将最近的网格点插入命中集,对于每个未命中,我们插入与每个像素相关的网格点,这些像素与扫描原点和每个扫描点之间的射线相交,不包括已经在命中集中的网格点。
每个以前未观测到的网格点都被分配一个概率\(phit\)或\(pmiss\),如果它在这些集合中的一个。
如果一个网格点x之前已经被观测过,那么就更新命中和未命中的概率,如下:
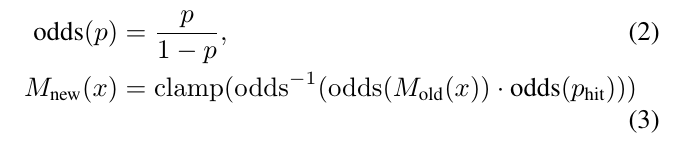
6.3. 在 scan matching使用Ceres
在将扫描插入子图之前,该帧相对于当前子图的位姿\(\xi\)使用Ceres的Scan matcher优化得到。Scan matcher的作用是寻找一个位姿pose,该位姿使子图中扫描点(激光点?)的概率最大化,可以写成一个非线性最小二乘的问题:
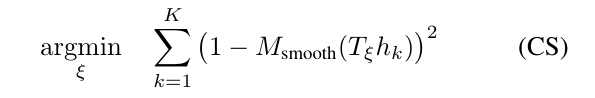
其中,\(T_\xi\)表示根据位姿\(\xi\)把激光扫描中的点(雷达坐标系下的点)转换到子图坐标系下。\(M_{smooth}: R^2 \rightarrow R\)是子图概率值的平滑函数。我们使用双三次插值,结果,会出现[0,1]之外的值,但可认为是无害的。
这种光滑函数的数学优化通常比网格的分辨率精度更高,由于这是一个局部优化,所以需要好的初始估计。IMU可以测量角速度可以用来估计旋转值\(\xi_\theta\)。在没有IMU的情况下,可以使用更高频率的扫描匹配或像素精确的扫描匹配方法,尽管这需要更大的计算量。
7. 回环
由于一帧扫描只与(包含几个最近扫描)的子图匹配,因此上面描述的方法会慢慢积累误差。
较大的空间通过创建许多小的子图来处理,我们的方法,优化所有扫描和子图的姿态,遵循稀疏姿态调整。每一个相对位姿所对应的激光扫描,都被插入到内存中储存,用来回环优化。除了这些相对位姿,其他的每一帧扫描和一帧子图之间的构成的所有匹配对也会被考虑到回环中,一旦该子图不再改变。扫描匹配(scan matcher)程序在后台运行,如果找到了合适的匹配,这个相关联的相对位姿会被加入到优化问题中。
7.1. 优化问题
回环优化,如scan matching,也可以使用非线性最小二乘问题来表示,每隔几秒,就使用Ceres对下面的优化问题进行求解:
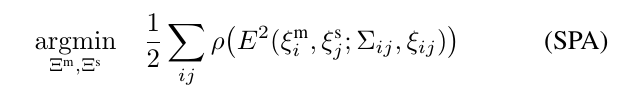
其中,世界坐标系下的子图的位姿\(\Xi^m=\{\xi_i^{m} \}_{i=1,\cdots,m}\)以及扫描的位姿\(\Xi^s=\{\xi_j^{s} \}_{j=1,\cdots,n}\)将由给定的约束进行优化。
这些约束采用相对位姿\(\xi_{ij}\)以及对应的协方差矩阵\(\Sigma_{ij}\)组成。对弈每一对{子图\(i\),扫描\(j\)},相对位姿\(\xi_{ij}\)描述了该激光扫描在子图坐标系中的匹配位置。协方差矩阵\(\Sigma_{ij}\)也可以被估计。这样一个约束的残差\(E\)可以如下表示,
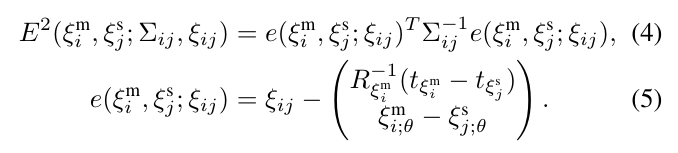
另外,损失函数\(\rho\)可以使用\(Huber\)损失,用来减少outliers (错误约束)带来的影响。这种情况常发生在局部特征相似的情况,如办公室的隔间。
7.2. 分枝定界的scan matching
7.2.1. 目标函数
系统对像素的准确度匹配优化问题感兴趣,即:
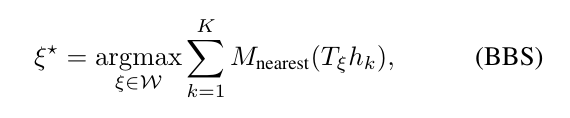
其中,\(w\)是搜索窗口,\(M_{nearest}\)是M扩展到最接近的像素点,这就是将网格点的值扩展到相应的像素。匹配的质量可以使用CS来进一步提高。
通过仔细选择步长来提高效率,选择角度步长\(\delta_\theta\)使得激光扫描到的最远的点不会移动超过\(r\),也就是一个像素的范围。使用余弦定理,可以得到:
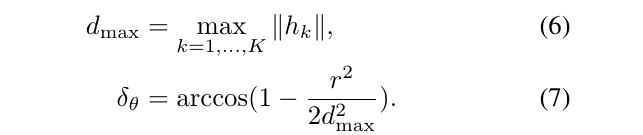
我们计算可以覆盖给定线性和角搜索窗口大小的整数步长,如给定\(W_x=W_y=7m\)和 \(W_\theta=30 \degree\),那么转换为像素就是:
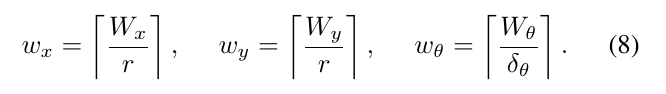
这将导致在估计的位姿\(\xi_0\)附近形成一个搜索集合,且\(\xi_0\)是搜索窗口的中心。
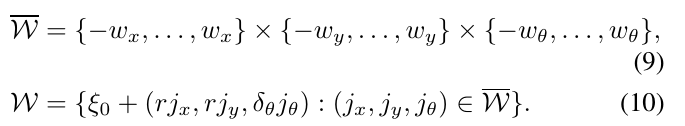
对应的寻找最优位姿\(\xi^{*}\)的算法可以写成如下流程,但对于搜索窗口的大小,我们认为它将是太慢。运算复杂度\(O(n^3)\)?

7.2.2. 分枝定界
为此,使用分枝定界法来高效的计算最优位姿\(\xi^{*}\),以便于在更大的搜索窗口进行搜索。一个通用的分枝定界算法流程如下:

其主要思想是将可能性的子集表示为树中的节点,其中根节点表示所有可能的解,在最优位姿搜索的这个情况就是搜索窗口W。
- 每个节点的子节点形成其父节点的一个分区,因此它们一起表示相同的一组可能性。
- 叶节点是单节点;每一个都代表一个可行的解决方案
- 注意到算法是精确的,它提供了与朴素方法相同的解决方案,其中的前提条件是只要内部某个节点\(c\)的得分\(Score(c)\)是其所有子节点得分的上限
- 在这种情况下,当一个节点有界(上限)时,这个节点的所有子节点就不存在比已知的最好的解决方案更好的解决方案
7.2.3. 分枝定界树的构建
为了将问题转换为分枝定界数搜索问题,需要确定节点选择、分支和上界计算的方法。
7.2.3.1. 节点选择
算法使用深度优先搜索(DFS)作为默认选择,该算法的效率很大程度上取决于被修剪的树。后一部分借助于DFS,它可以快速计算许多叶节点。
由于我们不希望添加坏的匹配作为回环约束,所以我们还引入了一个分数阈值,低于这个阈值时我们对于给出的结果不感兴趣。因为在实践中,这个门槛不会经常被超越,这降低了选择节点或寻找初始启发式解决方案的重要性。(降低了初值的敏感性)。
对于在DFS期间访问子节点的顺序,需要计算每个子节点得分的上界,首先访问最有希望的子节点和最大的上界,即如下:

- 最佳分数设置为给定的阈值
- 计算和储存集合\(C_0\)的每一个元素的得分
- 对集合\(C_0\)按得分排序,初始化堆栈,分数最高的在顶部。
- 如果堆栈\(C\)不为空,则进入遍历:
- 从堆栈\(C\)弹出顶部元素\(c\)(得分最高的)
- 如果\(c\)的得分比最佳分数高
- 同时也是一个叶子节点(表示一种可能的解决方案),就记录下此时\(c\)所代表的位姿\(\xi_c\),最佳分数也设置为新的值。
- 否则,若元素\(c\)不是一个叶子节点,即还没有展开到最底层,那么对元素\(c\)进一步展开,得到元素\(c\)的子集\(C_c\),计算和储存元素\(c\)的子集\(C_c\)里面每一个元素的得分,最后将\(C_c\)推入堆栈\(C\),按得分排序,最大分数在最顶部。
- 遍历堆栈\(C\)的所有元素之后,得到最佳分数和对应的位姿。
7.2.3.2. 分支法则
树中的每一个叶子节点由一组整数的元素\(c\)来描述,\(c=(c_x,c_y,c_\theta,c_h) \in Z^4\)。
在高度为\(c_h\)的节点有\(2^{c_h} \times 2^{c_h}\)种可能的平移,但是旋转量是固定的。即:
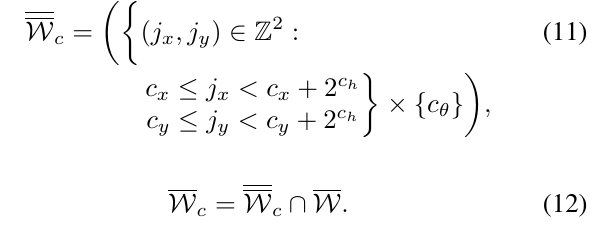
对于叶子节点,其高度\(c_h=0\),对应着一种可能的解决方案\(\xi_c=\xi_0+(rc_x,rc_y,\delta_\theta c_\theta)\),这个解的意思就是在给定初始值\(\xi_0\)的基础上加上一个偏移。
在算法3中,根节点包含了所有的可行解,不显式出现并分支成一组初始节点\(C_0\),在高度\(h_0\)包括了如下的搜索窗口:
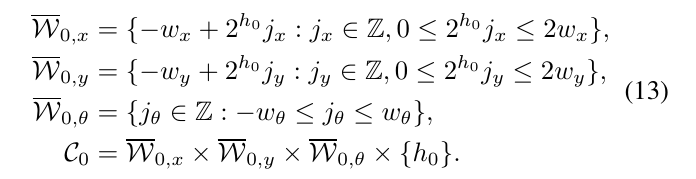
其中,\(w_x,w_y,w_\theta\)都是给定的搜索范围。
对于某一个高度为\(c_h>1\)的节点\(c\),又可以分支成4个高度为\(c_{h-1}\)的子节点:
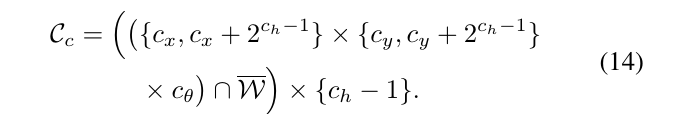
7.2.3.3. 计算上界
在计算量和质量的角度上考虑,选取以下来作为节点上界的计算。
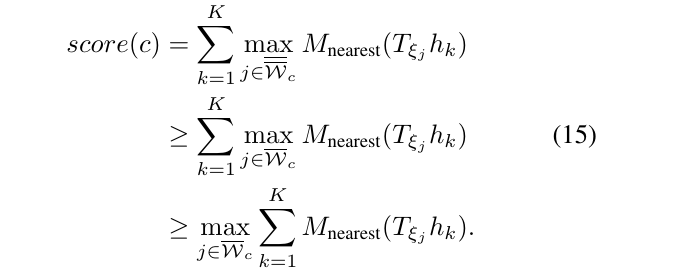
其中,\(\overline{W}\)是给定搜索窗口(全解),\(\overline {\overline {W_c}}\)是指定高度的某个节点所对应的全部可能的平移所组成的集合,而\(\overline{W_c}\)则是上述搜索窗口与平移集合的交集。
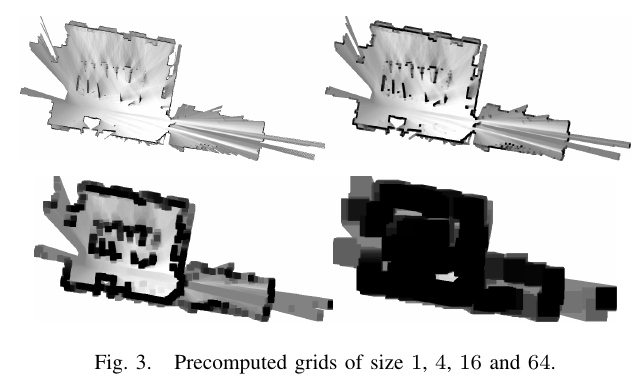
为了高效的计算出最大值,使用了预计算的网格地图\(M_{precomp}^{c_h}\)。为每一个可能的高度\(c_h\)预计算一个网格地图,可以使得计算量与扫描激光点的数量成线性。预计算的网格地图\(M_{precomp}^{c_h}\)与元地图有同样的像素结构(width × height),但是每个像素取的是\(2^h \times 2^h\)大小的范围内的最大值,如下:
为了确定上界,还计算指定高度的某个节点所对应的全部可能的平移所组成的集合了\(\overline {\overline {W_c}}\)的最高分数值,这个分数值大于或等于\(\overline{W_c}\)的最大值。那么,某一个高度\(c_h\)节点的上界可以按如下确定:
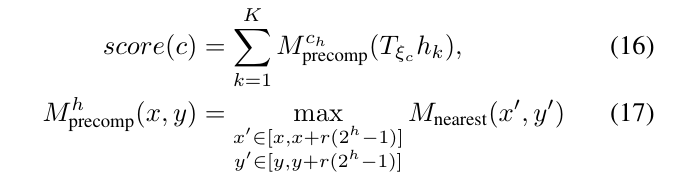
7.2.3.4. 操作流程
为了将构建(预计算网格地图)的计算工作量保持在较低的水平,我们要等到概率网格不再更新的时候,然后我们计算一组预计算的网格地图,并开始与之匹配。