1. Introduction:SVD分解(奇异值分解)
奇异值分解(Singular Value Decompositionm,简称SVD)是在机器学习领域应用较为广泛的算法之一,也是学习机器学习算法绕不开的基石之一。SVD算法主要用在降维算法中的特征分解、推荐系统、自然语言处理计算机视觉等领域。(也是PCA降维的核心之一)
奇异值分解(SVD)通俗一点讲就是将一个线性变换分解为两个线性变换,一个线性变换代表旋转,一个线性变换代表拉伸。
SVD是将一个矩阵分解成两个正交矩阵和一个对角矩阵,我们知道正交矩阵对应的变换是旋转变换,对角矩阵对应的变换是伸缩变换
2. 特征值分解
在学习SVD奇异值分解之前,先来看一下特征值分解
2.1. 矩阵特征值与特征向量
若有 \[ \begin{aligned} Ax=\lambda x \end{aligned} \]
其中,\(A \in R^{n \times n}\)是一个矩阵,如果上式成立,则称\(\lambda\)是矩阵\(A\)的特征值,向量\(x\)是\(\lambda\)对应的特征向量。
2.2. 特征分解
如果已经求出了矩阵\(A\)的\(n\)个特征值\(\lambda_1 \leq \lambda_2 \cdots \leq \lambda_n\),以及这\(n\)个特征值所对应的特征向量\(w_1,w_2,\cdots , w_n\),如果这n个特征向量线性无关,则矩阵A可以用以下特征分解表示:
\[ A=W\Sigma W^{-1} \]
其中, \[W=(w_1,w_2,\cdots,w_n)\]
\[ \begin{aligned} \Sigma= \begin{pmatrix} \lambda_1 & & & \\ & \lambda_2 & & \\ & & \cdots & \\ & & & \lambda_n \end{pmatrix} \end{aligned} \]
一般情况下,会把\(W\)的n个特征向量进行归一化,即\(||w_i||_2=1\)或者是\(w_i^{T}w_i=1\),归一化之后,这n个特征向量则是标准正交基,满足\(W^TW=I\)
实际上,这个操作就是线性代数里面的对角化操作。
特征值分解有一个前提:
- 分解的矩阵必须是方阵
对于不是方阵的矩阵,该如何进行分解? 这就是SVD的用处了
3. 奇异值分解(SVD)
对于一个非方阵的矩阵\(A_{m \times n}\)来说,其SVD分解可写成如下: \[ A=U\Sigma V^T \]
其中:
- \(U\)和\(V\)都是单位正交阵,则有\(UU^T=I\)、\(VV^T=I\),其中\(U\)为\(m \times m\)矩阵,\(V\)为\(n\times n\)矩阵
- \(\Sigma\)是一个\(m \times n\)矩阵,只有主对角线上的元素有值,其他元素均为0.
- 分解可如下表示
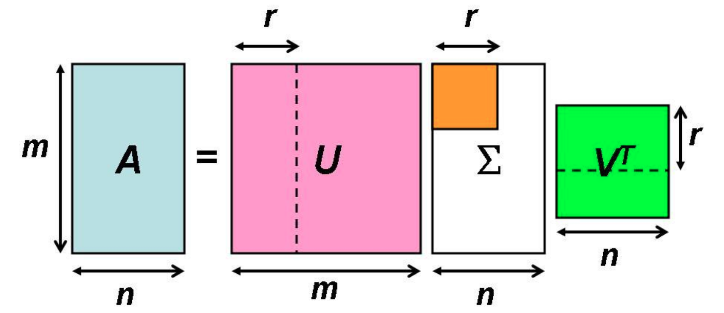
SVD分解的主要步骤就是求解\(U,\Sigma,V^T\),接下来继续讨论如何求解
3.1. 求解\(U\)
因为==>
\[ \begin{aligned} AA^T &=(U\Sigma V^T)(U\Sigma V^T)^T \\ &=U\Sigma V^TV\Sigma^TU^T \\ &=U\Sigma \Sigma^TU^T \end{aligned} \]
\[ \begin{aligned} A^TA &=(U\Sigma V^T)^T(U\Sigma V^T) \\ &=V\Sigma^TU^TU\Sigma V^T \\ &=V\Sigma^T\Sigma V^T \end{aligned} \]
其中,这里的\(\Sigma \Sigma^T\)和\(\Sigma^T \Sigma\)在矩阵维度上面不相等,但是对角线上的元素是相等的。 \[ \begin{aligned} \Sigma\Sigma^T = \left[ \begin{matrix} \sigma_1^2 & 0 & 0 & 0\\ 0 & \sigma_2^2 & 0 & 0\\ 0 & 0 & \ddots & 0 \\ 0 & 0 & 0 & \ddots \\ \end{matrix} \right]_{m\times m}\quad \Sigma^T\Sigma = \left[ \begin{matrix} \sigma_1^2 & 0 & 0 & 0\\ 0 & \sigma_2^2 & 0 & 0\\ 0 & 0 & \ddots & 0\\ 0 & 0 & 0 & \ddots\\ \end{matrix} \right]_{n\times n} \end{aligned} \]
所以==>
可以注意到,\(AA^T\)是方阵,于是对\(AA^T\)进行特征值分解,有
\[ \begin{aligned} M=(AA^T)&=W\Sigma W^{-1} \\ &=U\Sigma_u \Sigma_u^TU^T \end{aligned} \]
可得:
- \(AA^T\)进行特征值分解之后的特征向量矩阵\(W\)就是矩阵\(A\)的右奇异向量矩阵\(U\)
即: \[ W=V \]
3.2. 求解\(V\)
于是==>
同理可得:
- \(A^TA\)进行特征值分解之后的特征向量矩阵\(W_r\)就是矩阵\(A\)的左奇异向量矩阵\(V\)
即: \[ W_r=V \]
3.3. 求解\(\Sigma\)
因为==>
\[AA^T=U\Sigma \Sigma^TU^T\]
其中,
\[ \begin{aligned} \Sigma\Sigma^T = \left[ \begin{matrix} \sigma_1^2 & 0 & 0 & 0\\ 0 & \sigma_2^2 & 0 & 0\\ 0 & 0 & \ddots & 0 \\ 0 & 0 & 0 & \ddots \\ \end{matrix} \right]_{m\times m}= \left[ \begin{matrix} \lambda_1 & 0 & 0 & 0\\ 0 & \lambda_2 & 0 & 0\\ 0 & 0 & \ddots & 0\\ 0 & 0 & 0 & \ddots\\ \end{matrix} \right]_{m\times m} \end{aligned} \]
所以==>
- \(\Sigma\)的元素就是\(\Sigma\Sigma^T\)的主对角线元素的开方
- (也就是说,\(A\)的奇异值\(\sigma\)等于\(AA^T\)特征值的开方)
\[ \begin{aligned} \sigma_i=\sqrt{\lambda_i} \end{aligned} \]
3.4. 实际例子
3.4.1. 例1


3.4.2. 例2
3.5. SVD分解的结论
- 任意的矩阵A可以分解成3个矩阵
- 其中可得到\(U\)和\(V\)两个标准正交基
- \(\Sigma\)中的主对角线上的奇异值\(\sigma_i\)按大到小向右下角排列,值越大,表示该维度的信息重要性越大
3.6. SVD分解的应用
- 数据降维(取奇异值大的几个维度)
- 数据压缩(图片压缩),例子见:奇异值分解应用
- 求解非齐次线性方程组
- 求解齐次线性方程组最小二乘解