- 1. 1. PnP问题回顾
- 2. 2. EPnP
- 3. 3. 参数定义
- 4. 4. 确定世界坐标系的控制点\(c_{j}^w\)
- 5. 5. 确定权重\(\alpha_{ij}\)
- 6. 6. 确定相机坐标系的控制点\(c_{j}^c\)
- 6.1. 6.1. 构造约束
- 6.2. 6.2. 求解齐次方程组
- 6.3. 6.3. 选择正确的线性组合[\(\boldsymbol{x}=\sum_{i=1}^{N} \beta_i \boldsymbol{v_i} ~~, N=?\)]
- 6.4. 6.4. 优化\(\beta\)
- 6.5. 6.5. 恢复[R | t] ——ICP问题求解
- 7. EPnP总流程:
- 8. 6.6. 参考资料
1. PnP问题回顾
已知
- 世界坐标系下的3D点
- 这些3D点在相机坐标系下的, 经过相机模型投影形成的图像点(u,v)
- 相机内参矩阵K
求解
- 相机位姿Tcw(即世界坐标系到相机坐标系的变换)
2. EPnP
EPnP算法将世界坐标系中的3D坐标表示为一组虚拟的控制点的加权和。对于一般情形,EPnP算法要求控制点的数目为4,且这4个控制点不能共面。因为摄像头的外参未知,这四个控制点在摄像头参考坐标系下的坐标是未知的。而如果能求解出这四个控制点在摄像头参考坐标系下的坐标,我们就可以计算出摄像头的位姿。
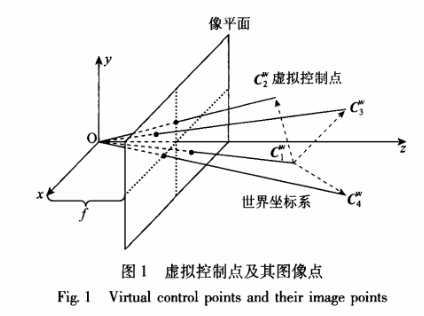
2.1. 摘要
EPnP主要idea是使用4个虚拟的控制点的加权来表示3D点的坐标, 使得求解[R,t]问题变成估计这些控制点在相机坐标系下的坐标的问题。
控制点在相机坐标系下的坐标又可以通过使用一个12x12矩阵的奇异值向量\(v_i\)的加权\(\beta_i v_i\)来表示(也就是齐次线性方程组的最小二乘解)。
最终, 问题变成了最优化一个具有少量约束的二次等式的问题来选取合适的\(\beta\)。另外,如果需要足够准确的值,那么可以通过闭式解的输出作为高斯牛顿迭代优化的初始值,使用优化方法来获取足够的精度。
2.2. 主要思路
使用一种方式来构造点云在相机坐标系下的表达,最终通过世界坐标系的点云和相机坐标系的点云进行ICP匹配。
3. 参数定义
3.1. 世界坐标系下的点
\[ p_i, ~~ i=1,2,\cdots,n \]
3.2. 4个控制点
注意: 这4个控制点不能在同一平面上
\[ \begin{aligned} c_j=\begin{bmatrix} c_{jx} \\ c_{jy} \\ c_{jz} \\ c_{jw} \end{bmatrix} , ~~ j=1,2,3,4 \end{aligned} \]
3.3. 使用控制点来表示世界坐标系下的点
\[ \begin{aligned} p_i^{w}=\sum_{j=1}^{4}\alpha_{ij}c_{j}^{w},~~~with \sum_{j=1}^{4} \alpha_{ij}=1 \end{aligned} \]
其中,
- \(\alpha_{ij}\)是齐次重心坐标\((Homogeneous~Barycentric~Coordinates)\)的权重,**在世界坐标系和相机坐标系都保持一致。[**这是个重要的假设]
- \(c_j^w\)表示4个控制点在世界坐标系的表示
3.4. 使用控制点来表示相机坐标系的点
同样的,有
\[ \begin{aligned} p_i^{c}=\sum_{j=1}^{4}\alpha_{ij}c_{j}^{c},~~~with \sum_{j=1}^{4} \alpha_{ij}=1 \end{aligned} \]
4. 确定世界坐标系的控制点\(c_{j}^w\)
理论上, 控制点可以任意选取. 但是实际实践中, 文章作者发现这个方法的稳定性取决于中心作为参考点
4.1. 第一个控制点
一般选择世界坐标系下3D点质心作为第一个控制点\(c_{1}^w\),即
\[ c_{1}^w=\frac{1}{n} \sum_{i=1}^{n} p_i^w \]
4.2. 其他控制点的确定
4.2.1. 计算世界坐标系参考点的去质心坐标
\[ \begin{aligned} A=q_i^{w}= \begin{bmatrix} p_1^{wT}-c_1^{wT} \\ \vdots \\ p_n^{wT}-c_1^{wT} \end{bmatrix} \end{aligned} \]
4.2.2. 对矩阵\(A^TA\)进行SVD分解
\[ A^TA=V\Sigma V^T \]
为什么只有V,可参见SVD分解
取分解后的前3个特征值\(\lambda_1,\lambda_2,\lambda_3\),以及对应的特征向量\(v_{1},v_{2},v_{3}\),这3个特征向量实际上就代表了点云的3个主方向,剩下的3个控制点使用这3个主方向来表示。
4.2.3. 剩下的3个控制点
\[ \begin{aligned} c_{2}^w &=c_{1}^w + \sqrt{\frac{\lambda_1}{n}} v_{1} \\ c_{3}^w &=c_{1}^w + \sqrt{\frac{\lambda_2}{n}} v_{2} \\ c_{4}^w &=c_{1}^w + \sqrt{\frac{\lambda_3}{n}} v_{3} \end{aligned} \]
5. 确定权重\(\alpha_{ij}\)
对于权重来说,不论是在世界坐标系还是相机坐标系下,它的值都是一样的,我们只须通过世界坐标和世界坐标系下得到控制点得到权重。
5.1. 世界坐标系下点的表达
\[ \begin{aligned} p_i^{w}=\sum_{j=1}^{4}\alpha_{ij}c_{j}^{w},~~~with \sum_{j=1}^{4} \alpha_{ij}=1 \end{aligned} \]
对上式进一步展开(齐次形式,因为控制点有4个),
\[ \begin{aligned} \begin{bmatrix} p_{i}^w \\ 1 \end{bmatrix} = \begin{bmatrix} c_{1}^w & c_{2}^w & c_{3}^w &c_{4}^w \\ 1 & 1 & 1 & 1 \end{bmatrix} \begin{bmatrix} \alpha_{i}^1 \\ \alpha_{i}^2 \\ \alpha_{i}^3 \\ \alpha_{i}^4 \end{bmatrix} \end{aligned} \]
5.2. 所以,\(\alpha\)可以按下式确定:
\[ \begin{aligned} \begin{bmatrix} \alpha_{i}^1 \\ \alpha_{i}^2 \\ \alpha_{i}^3 \\ \alpha_{i}^4 \end{bmatrix} = \begin{bmatrix} c_{1}^w & c_{2}^w & c_{3}^w &c_{4}^w \\ 1 & 1 & 1 & 1 \end{bmatrix}^{-1} \begin{bmatrix} p_{i}^w \\ 1 \end{bmatrix} \end{aligned} \]
5.3. 也可以按下面来确定(ORB_SLAM2采用的):
因为
\[ \begin{aligned} \begin{bmatrix} p_{i}^w \\ \end{bmatrix} = \begin{bmatrix} c_{1}^w & c_{2}^w & c_{3}^w &c_{4}^w \end{bmatrix} \begin{bmatrix} \alpha_{i}^1 \\ \alpha_{i}^2 \\ \alpha_{i}^3 \\ \alpha_{i}^4 \end{bmatrix} \\ \Longrightarrow \begin{bmatrix} c_1^w & c_2^w-c_1^w & c_3^w-c_1^w & c_4^w-c_1^w \end{bmatrix} \begin{bmatrix} 1 \\ \alpha_i^2 \\ \alpha_i^3 \\ \alpha_i^4 \end{bmatrix} \\ \Longrightarrow (p_{i}^w-p_0^{w})= \begin{bmatrix} c_2^w-c_1^w & c_3^w-c_1^w & c_4^w-c_1^w \end{bmatrix} \begin{bmatrix} \alpha_i^2 \\ \alpha_i^3 \\ \alpha_i^4 \end{bmatrix} \end{aligned} \]
所以:
\[ \begin{aligned} \begin{bmatrix} \alpha_i^2 \\ \alpha_i^3 \\ \alpha_i^4 \end{bmatrix} = \begin{bmatrix} c_2^w-c_1^w & c_3^w-c_1^w & c_4^w-c_1^w \end{bmatrix}^{-1} [p_{i}^w-p_0^{w}] \end{aligned} \]
\[ \alpha_i^1=1-\alpha_i^2-\alpha_i^3-\alpha_i^4 \]
6. 确定相机坐标系的控制点\(c_{j}^c\)
6.1. 构造约束
假设矩阵\(A\)相机内参, \(u_i\)为世界坐标系的点在经过相机模型之后的图像点, 则有:
\[ \begin{aligned} w_i \begin{bmatrix} \boldsymbol{u_i} \\ 1 \end{bmatrix} = w_i \begin{bmatrix} u_i \\ v_i \\ 1 \end{bmatrix} = A p_i^c = A\sum_{j=1}^{4}\alpha_{ij}c_{j}^c \end{aligned} \]
其中,
- \(w_i\)是投影的尺度参数
进一步展开, 得到
\[ \begin{aligned} w_i \begin{bmatrix} u_i \\ v_i \\ 1 \end{bmatrix} = A p_i^c & = A\sum_{j=1}^{4}\alpha_{ij}c_{j}^c \\ & = \begin{bmatrix} f_u & 0 & u_c \\ 0 & f_v & v_c \\ 0 & 0 & 1 \end{bmatrix} \sum_{j=1}^{4} \alpha_{ij} \begin{bmatrix} x_{j}^c \\ y_{j}^c \\ z_{j}^c \end{bmatrix} \end{aligned} \]
其中, \(c_{j}^c\)表示每个控制点在相机坐标系下的表示
\[ \begin{aligned} c_j^{c}= \begin{bmatrix} x_{j}^c \\ y_{j}^c \\ z_{j}^c \end{bmatrix} \end{aligned} \]
根据上面等式的最后一行,有
\[ w_i=\sum_{j=1}^{4} \alpha_{ij} z_{j}^c \]
将这个约束回代到等式的第1,第2行, 消去尺度因子\(w_i\), 可得
\[ \begin{aligned} \sum_{j=1}^{4} \alpha_{ij}f_{u}x_{j}^c+ \alpha_{ij}(u_c-u_i)z_{j}^c=0 \\ \sum_{j=1}^{4} \alpha_{ij}f_{v}y_{j}^c+ \alpha_{ij}(v_c-v_i)z_{j}^c=0 \end{aligned} \]
于是, 对于每一个相机坐标系的3D点, 都可以得到两个这样的齐次方程
于是, 当有n个参考点的时候, 可以得到如下齐次线性方程组:
\[ \begin{aligned} \boldsymbol{Mx}=0 \end{aligned} \]
在构造系数矩阵\(M\)的时候,注意,式中的求和\(\sum\)实际上是矩阵维度上的拼接,即\(\boldsymbol{M}\)和\(x\)的形式如下:
- 图中的\(c_{x0}\)等于上面公式中的\(x_{j}^c\)
- \(c_{y0}=y_{j}^c\)、\(c_{z0}=z_{j}^c\)
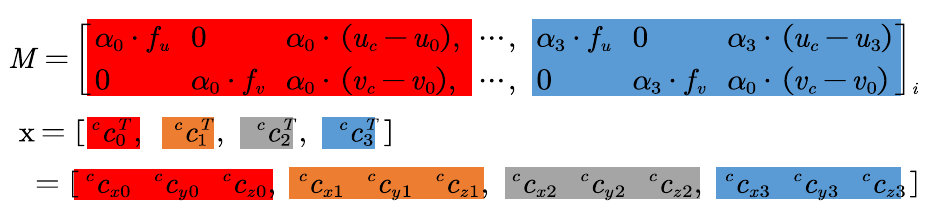
其中,
- \(\boldsymbol{x}=[c_{1}^{cT},c_{2}^{cT},c_{3}^{cT},c_{4}^{cT}]\) 是一个12维的向量, 也就是4个控制点的坐标,是未知数
- 矩阵\(A\)是一个\((2n \times 12)\)的矩阵.
- 与DLT不同,由于不涉及图像参考系统,我们不需要对2D投影进行归一化
6.2. 求解齐次方程组
上面得到的齐次线性方程组的解就是矩阵\(A\)的零空间, 可以表示成下面的形式:
\[ \boldsymbol{x}=\sum_{i=1}^{N} \beta_i \boldsymbol{v_i} \]
其中,
- \(\boldsymbol{v_i}\)是矩阵\(A\)经过SVD分解后得到的右奇异矩阵的列向量, 也就是奇异值对应的特征向量,维度是\(12\times 1\)
- \(\boldsymbol{v_i}\)可以通过对\(A^TA\)进行SVD分解得到, 并且\(A^TA\)只是一个\((12 \times 12)\)的矩阵
- 实际上, 计算\(A^TA\)是这个算法最花费时间的步骤, 具有\(O(n)\)的复杂度
6.3. 选择正确的线性组合[\(\boldsymbol{x}=\sum_{i=1}^{N} \beta_i \boldsymbol{v_i} ~~, N=?\)]
已知齐次线性方程组的解可以表示成\(A^TA\)的奇异值向量的线性组合, 问题实际上变成了求解\(\beta_i\)合适的值.
理论上, 当给定十分完美的数据(至少6个点以及一个准确的相机模型), 这个\(A^TA\)的零空间的维度是十分准确的是1, 因为仅仅只有尺度的不确定性.
对比下, 如果考虑一个不那么精确的相机模型, 那么\(A^TA\)的零空间维度变成4, 因为有4个控制点的深度不确定.
实验表明,一个带有大焦距的相机可能会有an affine model, 因此零空间的维度是不确定的, 可能是1到4之间的值. 其带来的影响如下图
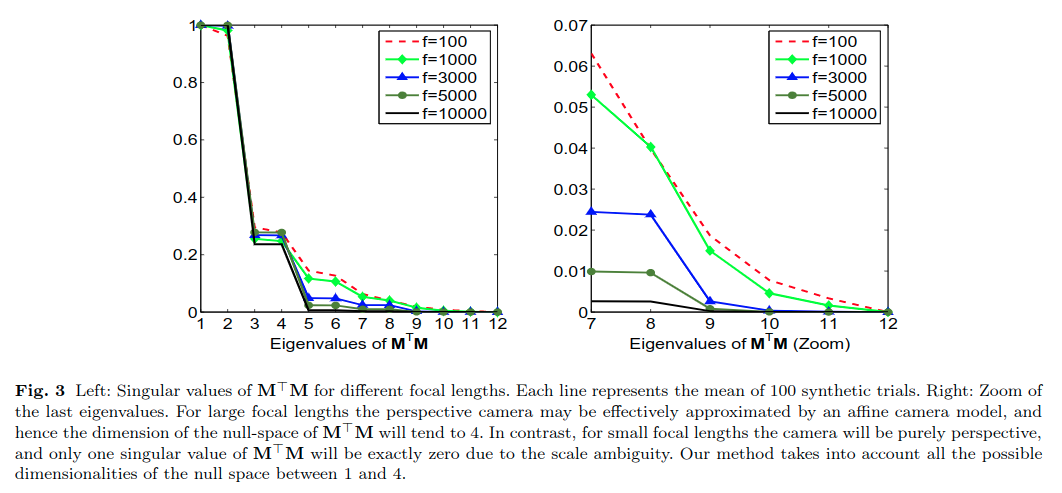
上图说明了, 矩阵\(A^TA\)的特征值个数与相机的焦距有关.
此外,由于噪声的存在,没有特征值严格为零,但可能很小.
另外, EPnP算法认为只需考虑特征值个数为\(N=1,2,3,4\)的情况, 当考虑了相机带有观测噪声时, N可能>5, 但是经过仿真实验表示, 没有必要考虑N>=5的情况
控制点之间必须保持一定的距离,这是为了保证控制点之间的距离可以使用几个少量的二次等式来表示, 用来求解系数\(\beta_i, i=1,2,3,4\)
因此, EPnp选择对\(N=1,2,3,4\)的情况都进行计算, 最后选择产生最小的重投影误差的情况作为solution
\[ \begin{aligned} res=\sum_{i} dist^2(K*[R|t] \begin{bmatrix} p_{ix}^w \\ p_{iy}^w \\ p_{iz}^w \\ 1 \end{bmatrix} , \boldsymbol{u_i}= \begin{bmatrix} u_i \\ v_i \end{bmatrix}) \end{aligned} \]
下面, 从N的各种情况来讨论这个二次约束
6.3.1. N=1
当N=1的时候,可以简化为\(x=\beta v\),\(\beta\)(标量)的求解过程如下:
\[ \begin{aligned} &\because x^{c}=\beta v = [c_1^{cT},c_2^{cT},c_3^{cT},c_4^{cT}]_{1 \times 12} \\ \end{aligned} \]
在相机坐标系下的控制点\(c_{i}^{c}\)之间的距离可以看做是等于世界坐标系下的控制点\(c_{i}^{w}\)之间的距离,即
\[ \begin{aligned} And: ~~~~~~~ dist(c_{i}^{c},c_{j}^{c}) &=dist(c_{i}^{w},c_{j}^{w}) \\ ||\beta v^{[i]}-\beta v^{[j]}||^2 &=||c_{i}^{w}-c_{j}^{w}||^2 \end{aligned} \]
其中,\(v^{[i]}\)表示向量\(v\)(或者是\(x\))中与第i个控制点相关的3维的向量,一共有4个,即\(i=1,2,3,4\).
又因为世界坐标系下的控制点之间的距离\(||c_{i}^{w}-c_{j}^{w}||\)是已知的,所以\(\beta\)的闭式解(解析解)可以写成如下
\[ \begin{aligned} \beta = \frac {\sum_{\{i,j\} \in [1:4]} ||v^{[i]}-v^{[j]} || \cdot ||c_{i}^{w}-c_{j}^{w}||} {\sum_{\{i,j\} \in [1:4]} ||v^{[i]}-v^{[j]}||^2} \end{aligned} \]
6.3.2. N=2
N=2时,有
\[ x=\beta_1 v_1 +\beta_2 v_2 \]
控制点的距离约束可写成:
\[ \begin{aligned} dist(c_{i}^{c},c_{j}^{c}) =dist(c_{i}^{w},c_{j}^{w}) \\ \Longrightarrow ||(\beta_1 v_1^{[i]}+\beta_2 v_2^{[i]})-(\beta_1 v_1^{[j]}+\beta_2 v_2^{[j]})||^2 &=||c_{i}^{w}-c_{j}^{w}||^2 \\ \Longrightarrow ||(\beta_1 v_1^{[i]}-\beta_1 v_1^{[j]})+(\beta_2 v_2^{[i]}-\beta_2 v_2^{[j]})||^2 &=||c_{i}^{w}-c_{j}^{w}||^2 \\ \Longrightarrow ||\beta_1 \underbrace{(v_1^{[i]}- v_1^{[j]})}_{V_1^{[ij]}}+\beta_2 \underbrace{(v_2^{[i]}- v_2^{[j]})}_{V_2^{[ij]}}||^2 &=||c_{i}^{w}-c_{j}^{w}||^2 \end{aligned} \]
整理得到
\[ \begin{aligned} \beta_1^2 {V_1^{[ij]}}^T V_1^{[ij]} +2 \beta_1 \beta_2 {V_1^{[ij]}}^T V_2^{[ij]} + \beta_2^2 {V_2^{[ij]}}^T V_2^{[ij]} &=||c_{i}^{w}-c_{j}^{w}||^2 \\ \Longrightarrow \beta_{11} {V_1^{[ij]}}^T V_1^{[ij]} +2 \beta_{12} {V_1^{[ij]}}^T V_2^{[ij]} + \beta_{22} {V_2^{[ij]}}^T V_2^{[ij]} &=||c_{i}^{w}-c_{j}^{w}||^2 \end{aligned} \]
对上式左侧展开,可以得到关于\(\beta_1 \beta_1\)、\(\beta_1 \beta_2\)、\(\beta_2 \beta_2\)的二次项,将其分别表示为\(\beta_{11},\beta_{12},\beta_{22}\),把这三项作为未知数。
线性化求解:也就是把这个非线性方程线性化,把二次的未知数用一次未知数替换
因为有4个控制点,每两个控制点可以构成上面的一个线性化方程,那么一共可以构成\(C_{4}^{2}=6\)个方程,即有:
\[ \begin{aligned} \boldsymbol{L} \boldsymbol{\beta} = \boldsymbol{\rho} \end{aligned} \]
其中,
- \(\boldsymbol{L}\)是一个\(6 \times 3\)的矩阵,由系数\(V_1^{[ij]}\)和系数\(V_2^{[ij]}\)组成
- \(\boldsymbol{\rho}\)是一个\(6\)维向量,代表的是控制点之间的平方距离\(||c_{i}^{w}-c_{j}^{w}||^2\)
- \(\boldsymbol{\beta}=[\beta_{11},\beta_{12},\beta_{22}]^T\)则是待求的未知数
- 上面方程的求解使用了\(\boldsymbol{L}\)矩阵的伪逆矩阵,还要选择\(\beta\)的符号来使得相机坐标系下的所有点\(p_{i}^c\)都具有正的深度
原文提到: 求解得到\(\boldsymbol{\beta}\),并进一步分解得到\(\beta_1\)和> \(\beta_2\)之后,可进一步调整\(\beta_1\)和\(\beta_2\)的值:
- 使用下面公式求解得到一个通用的尺度\(\beta\)来满足\(c_{i}^{c}> =\beta(\beta_1 v_1^{[i]}+\beta_2 v_2^{[i]})\)
\[ \begin{aligned} \beta =\frac{\sum_{\{i,j\} \in [1:4]} ||v^{[i]}-v^{[j]} || \cdot ||c_{i}^{w}-c_{j}^{w}||}{\sum_{\{i,j\} \in [1:4]} ||v^{[i]}-v^{[j]}||^2} \end{aligned} \] 这是[不理解的地方]
6.3.3. N=3
N=3的情况与N=2的情况处理方法基本一致,此时未知数有\(\boldsymbol{\beta}=[\beta_{11},\beta_{12},\beta_{13},\beta_{22},\beta_{23},\beta_{33}]^T\),一共6个未知数。
同理,因为有4个控制点,每两个控制点可以构成上面的一个线性化方程,那么一共可以构成\(C_{4}^{2}=6\)个方程,即有:
\[ \begin{aligned} \boldsymbol{L} \boldsymbol{\beta} = \boldsymbol{\rho} \end{aligned} \]
其中,
- \(\boldsymbol{L}\)是一个\(6 \times 6\)的矩阵
- 求解这个非齐次线性方程组,与前面不同的是,这里可以直接求逆而不是求伪逆。
6.3.4. N=4
N=4时,继续尝试使用线性化的方法,此时未知数有\(\boldsymbol{\beta}=[\beta_{11},\beta_{12},\beta_{13},\beta_{14},\beta_{22},\beta_{23},\beta_{24},\beta_{33},\beta_{34},\beta_{44}]\),一共10个未知数。所以,4个控制点产生的6个距离约束在这里已经不够用了,论文提出使用重线性化方法
注意到:
- \(\beta_{ab} \beta_{cd}=\beta_a \beta_b \beta_c \beta_d=\beta_{a'} \beta_{b'} \beta_{c'} \beta_{d'}\)
- \(\{a',b',c',d'\}\)是对\(\{a,b,c,d\}\)的排列,即通过一些等价来介绍系数
- 例如:假设已知\(\beta_{11} ,\beta_{12} ,\beta_{13}\),则\(\beta_{23}\)可表示为\(\beta_{23}=\frac{\beta_{12} \beta_{13}}{\beta_{11}}\)
- 利用这个思想来减少未知数的个数
6.3.5. 除了上面各种情况的闭式解,还有一般形式的近似解(ORB_SLAM2采用的)

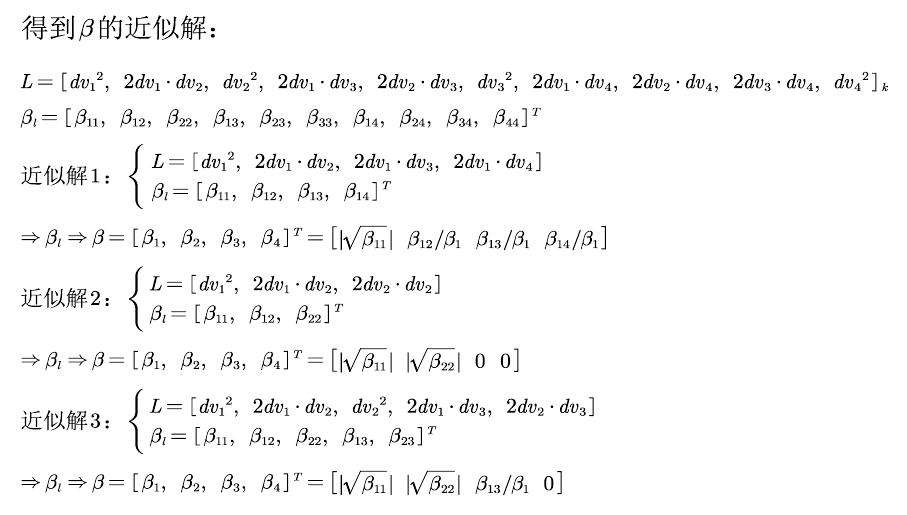
6.4. 优化\(\beta\)
经过上面的步骤,已经得到了关于\(\beta\)的闭式解
接下来通过使得下面的目标函数最小化,来对\(\boldsymbol{\beta}=[\beta_1,\beta_2,\beta_3,\beta_4]^T\)进行优化,求出更精确的\(\beta\)。
6.4.1. 残差
\[ e_{i,j}(\beta)=||c_i^c - c_j^c||^2 - ||c_i^w - c_j^w||^2 \]
6.4.2. 目标函数
\[ \begin{aligned} D =\sum_{(i,j),s.t.i<j} (||c_i^c - c_j^c||^2 - ||c_i^w - c_j^w||^2)^2 \end{aligned} \]
6.4.3. 优化目标
\[ \begin{aligned} \beta^*= \argmin_{\beta} \sum_{(i,j),s.t.i<j} (||c_i^c - c_j^c||^2 - ||c_i^w - c_j^w||^2)^2 \end{aligned} \]
其中,
- 世界坐标系下的控制点之间的距离\(||c_i^w - c_j^w||^2\)是已知的
- 相机坐标系下的控制点可以使用\(\beta\)作为系数,是矩阵\(A^TA\)奇异值向量的线性组合:
\[ c_{i}^{c}=\sum_{j=1}^{4} \beta_{j} v_{j}^{[i]} \]
又因为\(D_{k}^w=D_{ij}^w=||c_i^w - c_j^w||^2\)已知,所以接下来并不关注这部分
目标函数中,需要关注的是相机坐标系下的控制点距离这个部分: \[ \begin{aligned} D_{k}^c=D_{ij}^c &=||c_{i}^c-c_{j}^c|| \\ &= ||(\beta_1 v_{1}^i+\beta_2 v_{2}^i +\beta_3 v_{3}^i +\beta_4 v_{4}^i)-(\beta_1 v_{1}^j+\beta_2 v_{2}^j +\beta_3 v_{3}^j +\beta_4 v_{4}^j)||^2 \\ &=||\beta_1 \underbrace{(v_1^i-v_1^j)}_{dV_{1k}}+\beta_2 \underbrace{(v_2^i-v_2^j)}_{dV_{2k}}+\beta_3 \underbrace{(v_3^i-v_3^j)}_{dV_{3k}}+\beta_4 \underbrace{(v_4^i-v_4^j)}_{dV_{4k}}||^2 \\ &=\beta_1^2 [dV_{1k}]^T [dV_{1k}] + 2 \beta_1 \beta_2 [dV_{1k}]^T [dV_{2k}] + 2 \beta_1 \beta_3 [dV_{1k}]^T [dV_{3k}] + 2\beta_1 \beta_4 [dV_{1k}]^T[dV_{4k}]\\ &+\beta_2^2 [dV_{2k}]^T [dV_{2k}]+ 2 \beta_2 \beta_3 [dV_{2k}]^T[dV_{3k}] + 2 \beta_2 \beta_4 [dV_{2k}]^T[dV_{4k}]\\ &+ \beta_3^2 [dV_{3k}]^T[dV_{3k}] + 2\beta_3 \beta_4 [dV_{3k}]^T[dV_{4k}] \\ &+ \beta_4^2 [dV_{4k}]^T[dV_{4k}] \\ &= \boldsymbol{L\beta} \end{aligned} \]
6.4.4. 求解雅克比
\[ \begin{aligned} J=\frac{\partial D_{6 \times 1}}{\partial \beta^T} &=\frac{\partial [\sum_{k=1}^{6} D_{k}^{c}]}{\partial \beta^T} =\sum_{k=1}^{6} \frac{\partial [D_{k}^{c}]}{\partial [\beta_1,\beta_2,\beta_3,\beta_4]} \\ &=\sum_{k=1}^{6} 2 \begin{pmatrix} [dV_{1k}]^T[dV_{1k}] + \beta_2 [dV_{1k}]^T[dV_{2k}] + \beta_3 [dV_{1k}]^T[dV_{4k}] + \beta_4 [dV_{1k}]^T[dV_{4k}] \\ \beta_1 [dV_{1k}]^T[dV_{2k}] + [dV_{2k}]^T[dV_{2k}] + \beta_3 [dV_{2k}]^T[dV_{3k}]+ \beta_4 [dV_{2k}]^T[dV_{4k}] \\ \beta_1 [dV_{1k}]^T[dV_{3k}] + \beta_2 [dV_{2k}]^T[dV_{3k}] + [dV_{3k}]^T[dV_{3k}] + \beta_4 [dV_{3k}]^T[dV_{4k}] \\ \beta_1 [dV_{1k}]^T[dV_{4k}] + \beta_2 [dV_{2k}]^T[dV_{4k}] + \beta_3 [dV_{3k}]^T[dV_{4k}] + [dV_{4k}]^T[dV_{4k}] \end{pmatrix}_{4 \times 1}^T \\ &= \sum_{k=1}^6 2 J_{k,1 \times 4} \\ &= J_{6 \times 4} \end{aligned} \]
其中,
- \(D_{6 \times 1}\)是控制点间的距离\(C_{4}^2=6\),是6维向量
- \(D_{k}^c\)是某两个控制点之间的距离,是标量
- \(\boldsymbol{\beta}=[\beta_1,\beta_2,\beta_3,\beta_4]^T\)是未知数,是4维列向量
- 上面的求和\(\sum_{k=1}^6\)不是相加,只是在维度上进行拼接
6.4.5. 增量方程
\[ \boldsymbol{J^TJ} \delta \boldsymbol{\beta} = -\boldsymbol{J^T} D_{6 \times 1} \]
6.4.6. 进行迭代
通过迭代,可以对\(\beta\)的闭式解进一步调整优化,达到更高精度
6.5. 恢复[R | t] ——ICP问题求解
若变换关系为:
\[ p_i^c=R_{cw}p_i^w + t_{cw} \]
接下来求解\(R_{cw},t_{cw}\)
6.5.1. 计算控制点在相机坐标系的坐标\(c_{i}^c\)
\[ c_{i}^c=\sum_{j=1}^N \beta_{j}v_{j}^{[i]} ~~ i=1,2,3,4 \]
- \(c_{i}^c\) 是控制点的坐标,是\(3 \times 1\)向量
- \(v_{j}^{[i]}\) 是第j个特征值对应的特征向量的第i个控制点的分量,如果是第1个控制点,则对应前3个元素\(v_{[j,1:3]}\),是一个3维向量
- \(\beta_j\)是线性组合的权重
6.5.2. 利用控制点\(c_{i}^c\)计算n个参考点在相机坐标系的坐标
\[ p_i^c=\sum_{j=1}^4 \alpha_{ij}c_{j}^c , ~~~ i=1,2,\cdots,n \]
- 每个点都对应一组\(\alpha_i=[\alpha_{i1},\alpha_{i2},\alpha_{i3},\alpha_{i4}]\)值
6.5.3. 计算相机坐标系下参考点\(\{p_{i}^c \}_{i=1,\cdots,n}\)的质心\(p_0^c\)和去质心坐标
\[ \begin{aligned} p_0^c=\frac{1}{n} \sum_{i=1}^n p_{i}^c \\ q_i^{c}=\begin{bmatrix} p_1^{cT}-p_0^{cT} \\ \vdots \\ p_n^{cT}-p_0^{cT} \end{bmatrix} \end{aligned} \]
6.5.4. 计算世界坐标系下参考点\(\{p_{i}^w \}_{i=1,\cdots,n}\)的质心\(p_0^w\)和去质心坐标
\[ \begin{aligned} p_0^w=\frac{1}{n} \sum_{i=1}^n p_{i}^w \\ q_i^{w}=\begin{bmatrix} p_1^{wT}-p_0^{wT} \\ \vdots \\ p_n^{wT}-p_0^{wT} \end{bmatrix} \end{aligned} \]
6.5.5. 开始进行ICP求解
ICP求解可参见《视觉SLAM14讲-第二版P197》
6.5.5.1. 先求旋转R
令
\[ W_{3 \times 3}=q_i^{cT} q_i^{w} \]
对\(W_{3 \times 3}\)进行SVD分解,得
\[ W_{3\times3}=U \Sigma V^T \]
为了满足\(RR^T=I\),把SVD分解得到的奇异值矩阵\(\Sigma\)变成\(I\)
得到旋转矩阵\(R\)
\[ R=UV^T \]
如果旋转矩阵\(R\)的行列式\(\det R<0\),那么取\(R=-R\)
6.5.5.2. 再求平移t
\[ t=p_0^c-Rp_0^w \]
EPnP总流程:
