正态分布变换(The Normal Distributions Transform)

算法提出
Biber和Straer提出了二维数据配准的正态分布变换(NDT)方法。该算法中的关键元素是参考扫描的表示。不是将当前扫描直接匹配到参考扫描的点,而是通过正态分布的线性组合来模拟在特定位置找到表面点的可能性。
算法应用
- 点云配准
- 地图匹配
算法特点
计算正态分布是一个一次性的工作(初始化),不需要消耗大量代价计算最近邻搜索匹配点。概率密度函数在两幅图像采集之间的时间可以离线计算出来
其他配准算法
ICP
- 要剔除不合适的点对(点对距离过大、包含边界点的点对)
- 基于点对的配准,并没有包含局部形状的信息
IDC
- ICP的一种改进,采用极坐标代替笛卡尔坐标进行最近点搜索匹配
PIC
- 考虑了点云的噪音和初始位置的不确定性
Point-based probabilistic registration
Gaussian fields
- 和NDT正态分布变换类似,利用高斯混合模型考察点和点的距离和点周围表面的相似性
Likelihood-field matching——随机场匹配
CRF匹配
Branch-and-bound registration
Registration using local geometric features
2D-NDT基本原理
NDT算法论文原文是从2D角度描述的。
概率密度计算
NDT利用局部正态分布建立了一次激光扫描所有重建二维点的分布模型,首先,将机器人周围的二维空间细分为固定大小的网格(类似于占据栅格地图),然后对于每一个单元,进行下面3个操作
- 收集在这个窗口内的所有2D点
- 计算2D点集的质心\(q=\frac{1}{n}\sum_{i} x_i\)
- 计算协方差矩阵\(\Sigma=\frac{1}{n}\sum_i(x_i-q)(x_i-q)^T\)
那么,在这个单元cell内观测到一个样本在该2D点\(\boldsymbol{x}=(u,v)^T\) 的概率可以用下面的正态分布来描述:
\[ \begin{aligned} p(x) \sim \exp (-\frac{(x-q)^T \Sigma^{-1}(x-q)}{2}) \end{aligned} \]
与占据栅格类似,NDT建立了平面的网格细分,但是占据栅格代表的是该栅格被占据的概率,而NDT的栅格代表的是在一个单元(cell)内的每个位置上,观测到一个样本的概率。这个操作有什么好处?好处在于使用概率密度的形式对二维平面进行了分段连续可微的描述。
在进一步描述example之前,需要提出两点需要注意的地方
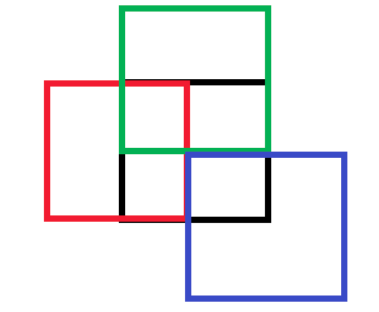
为了最小化离散化的影响,我们决定使用四个重叠的网格,首先放置一个边长为l的单网格,第二个则水平平移\(\frac{l}{2}\)长度,第三个则垂直方向平移\(\frac{l}{2}\)长度,而最后一个则水平和垂直都平移\(\frac{l}{2}\)长度。如下图所示,现在每个2D点都落入到这4个cell里面,因此,如果计算一个点的概率密度,即对所有四个单元的密度进行评估,并对结果进行求和。但是在下面的讨论中,暂时不考虑这样的情况,只需考虑只有1个cell即可。
另外一个点就是,如果在一个完全没有噪声的理想情况下,协方差矩阵会变成奇异的,无法求逆。在实际情况中,协方差矩阵有时候十分接近奇异,为了避免这种情况,进行检查,检查协方差矩阵的最小特征值是否至少是最大特征值的0.001倍,如果不是,则设置该值。
下图1展示了对激光扫描进行NDT之后的结果:

右图是NDT结果,这是通过计算每个点的概率密度得到的,高亮的部分表示着该处有较大的概率密度。接下来讨论这个变换怎么发挥作用在匹配中。
帧间配准(匹配)
给定两个机器人坐标系之间的空间映射T, \[ \begin{aligned} T= \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos \phi & -\sin \phi \\ \sin \phi & \cos \phi \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} t_x \\ t_y \end{pmatrix} \end{aligned} \]
其中,\((t_x,t_y)^T\)表示平移,\(\phi\)表示旋转——(两帧之间),帧间匹配就是要求出平移和旋转的量。
本文提出的基本流程是:
- 对第一帧进行NDT处理
- 参数(R,t)初始化,可设置为0或者使用里程计的数据
- 对于第二帧的每一个样本,利用待优化参数将第二帧的点反投影到第一帧的坐标系中
- 确定每个映射点对应的正态分布 ?
- 参数(R,t)的得分是通过评估每个映射点的分布并对结果求和来确定的
- 计算一个新的参数估计试图优化评分。这是通过执行牛顿算法的一个步骤完成的
- 重复,直到收敛
前4步就是前文所说的计算NDT变换,接下来详细介绍剩下的步骤
参数约定:
- 待优化参数\(\boldsymbol{T}()=\boldsymbol{P}=(p_i){i=1,2,3}=(t_x,t_y,\phi)^T\)
- 第二帧的第i个扫描点\(x_i\)
- 第二帧的第i个扫描点反投影回第一帧坐标系后得到的点\(x_i'=T(x_i,\boldsymbol{P})\)
- \(\Sigma_i,q_i\)分别是第二帧反投影点\(x_i'\)的联合高斯分布的协方差矩阵和均值,在第一帧的NDT变换中查找
评分函数
\[ score(p)=\sum_i \exp ( \frac{-(x_i'-q_i)^T \Sigma_i^{-1}(x_i'-q_i)}{2}) \]
这个其实就是联合高斯分布的表达,其中\(\Sigma_i^{-1}\)就是信息矩阵,也就是协方差矩阵的逆
牛顿迭代法优化
由于优化问题通常被描述为最小化问题,我们将采用这个约定的符号。最优化可以表示为最小化\(-socre\)。牛顿迭代法可以表示为求解增量方程
\[ \boldsymbol{H\Delta p}=-\boldsymbol{g} \]
其中,
- \(\boldsymbol{g}\)是函数\(f()\)的梯度转置,也就是雅克比
- \(\boldsymbol{H}\)是对应的海森矩阵
这个方程的解是一个增量\(\Delta p\),用来更新估计值:
\[ \boldsymbol{p} \leftarrow \boldsymbol{p} +\Delta \boldsymbol{p} \]
如果矩阵\(H\)是正定的,那么\(f(\boldsymbol{p})\)将会在增量\(\Delta \boldsymbol{p}\)的方向减小,否则使用\(\boldsymbol{H}'=\boldsymbol{H}+\lambda I\)来代替\(\boldsymbol{H}\),其中\(\lambda\)用来使得矩阵\(\boldsymbol{H}\)变成正定。
这个算法使用函数\(-score\),通过收集方程3中所有和的偏导数来建立梯度和海森矩阵。
下面的\(x_i\)将表示第i帧的点集,不再是第i个点?
于是,有 \[ q=x_i'-q_i \]
所以,优化的目标函数可以写成
\[ -score= s =- \exp \frac{- \boldsymbol{q^T} \Sigma^{-1} \boldsymbol{q} }{2} \]
于是,目标函数对优化变量的梯度为
\[ \begin{aligned} \bar{g_i} &= - \frac{ \partial s}{ \partial p[i]}= - \frac{ \partial s}{ \partial q} \frac{q}{p[i]} \\ &= \boldsymbol{q^T} \Sigma^{-1} \frac{ \partial q}{ \partial p[i]} \exp \frac{- \boldsymbol{q^T} \Sigma^{-1}q}{2} \end{aligned} \]
根据变换等式2,使用线性化的来表示,有
\[ \begin{aligned} u' = \cos (p[3]) u -\sin(p[3]) v+ p[1]\\ v' = \sin (p[3]) u -\cos(p[3]) v + p[2] \end{aligned} \]
对应的雅克比可写成
\[ \begin{aligned} \boldsymbol{J_T}= \frac{\partial \boldsymbol{q} }{\partial \boldsymbol{T} }=\frac{\partial \boldsymbol{q} }{\partial \boldsymbol{P} }= \begin{pmatrix} 1 & 0 & -x \sin \phi -y \cos \phi \\ 0 & 1 & x \cos \phi - y \sin \phi \end{pmatrix} \end{aligned} \]
海森矩阵\(\boldsymbol{H}\):
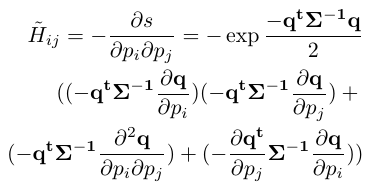
其中,投影后的去质心点集\(\boldsymbol{q}\)对变换\(p[i],p[j]\)的二阶导\(\frac{\partial ^2 \boldsymbol{q} }{ \partial p[i] \partial p[j]}\)可以如下表示:
\[ \frac{ \partial ^2 \boldsymbol{q} }{ \partial p_i \partial p_j}= \left \{ \begin{aligned} \begin{pmatrix} -x \cos \phi + y \sin \phi \\ -x \sin \phi - y \cos \phi \end{pmatrix} ~~ i=j=3 \\ \begin{pmatrix} 0 \\ 0 \end{pmatrix} ~~~~~~~~~~~~~~~ otherwise \end{aligned} \right. \]
注意:上面的\(p[i],p[j]\)都是指同一个变换\(P\)里面的某个元素\(t_x,t_y, \phi\)其中一个。
从这些方程可以看出,建立梯度和海森矩阵的计算成本较低,每点只有一次对指数函数的调用和少量的乘法。三角函数计算仅与估计的角度\(\phi\)有关,因此每次迭代都需要计算一次。
应用于位置跟踪
下面把参考的激光扫描称为关键帧,在时间\(t=t_k\),算法执行一下流程
- 设置一个从\(t_k-1\)到\(t_k\)的运动估计作为初值\(\delta\)
- 将当前帧的激光扫描点根据这个\(\delta\)反投影到上一个时刻的机器人坐标系下
- 使用当前帧的扫描、参考关键帧的NDT以及新的运动估计\(\delta\)来实现优化迭代
- 检查参考关键帧与当前帧是否比较靠近,如果是,则继续迭代,否则,采用上一次成功匹配的激光扫描作为新的关键帧。
判断一个扫描是否仍然足够近是基于一个简单的经验标准,涉及到关键帧和当前帧之间的平移和角距离以及最终的评分.
SLAM上的应用
定义地图就是对关键帧的采集以及各个关键帧的位姿。
对多次扫描进行定位
对于地图上的每帧的扫描\(i\),都拥有其位姿,位姿指该帧在全局坐标系下的,当前机器人姿态由旋转矩阵R和平移向量t表示
添加关键帧以及优化地图
地图是由一些关键帧以及它们的全局坐标系位姿组成的,如果当前扫描与地图的重叠太小,那么只取到最后一次成功匹配的扫描来组成地图。然后,每个重叠的扫描分别匹配到新的关键帧,产生两个扫描之间的相对位姿,这意味着需要维护一个图,其中包含成对匹配结果的信息。
在这个图里面,每个关键帧都使用一个节点来代表,每个节点维护着对应关键帧的世界坐标系的位姿。两个节点之间的边表示对应的扫描已经成对匹配,并维护着两个扫描之间的相对位姿,作为优化的约束条件。
当一个新的关键帧插入,地图会通过优化损失函数来调整所有关键帧的位姿来进行调整。关键帧之间两两配准的结果被用来定义每一对匹配的二次误差模型如下:两次扫描的全局位姿参数可用来表示两次扫描之间的相对位姿。
如果使用\(\Delta T\)来表示(使用两次扫描的全局位姿所构成的相对位姿)与(使用NDT匹配算法得到的相对位姿)之间的差,那么评分模型可以使用下面来描述
\[ socre'(\Delta T)= score + \frac{1}{2} (\Delta T)^T H (\Delta T) \]
这种全局优化的做法,当关键帧的数量变得很大的时候,难以再实时进行,因为待优化的参数随关键帧呈线性增长\(3N-3\),每个关键帧都需要3个参数,后面减3是因为第一个关键帧的位姿固定为(0,0,0),为了减少在零空间的漂移,采用固定第一帧的做法。
为了避免这个问题,文章采用使用局部图的思想,只对一个局部地图进行优化,这个局部子图通过遍历所有的关键帧,只有与当前帧相连不超过3条边的,才参与组成这个局部子图。我们现在只针对参数优化上面的错误函数,这些参数属于这个子图中包含的关键帧。
当然,如果如果要形成回环,我们将不得不优化所有关键帧。
文章实现效果
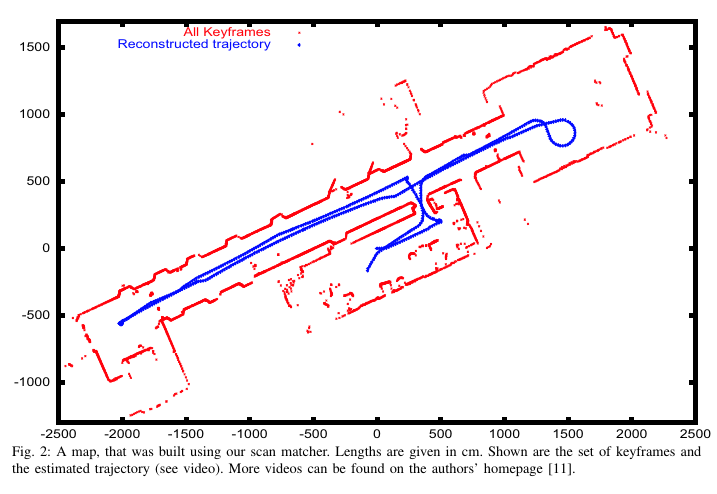
2020-03-06更新: PCL中关于2D-NDT的代码及注释
PCL代码基本与论文一致
ndt_2d.h 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
namespace pcl
{
/** \brief @b NormalDistributionsTransform2D provides an implementation of the
* Normal Distributions Transform algorithm for scan matching.
*
* This implementation is intended to match the definition:
* Peter Biber and Wolfgang Straßer. The normal distributions transform: A
* new approach to laser scan matching. In Proceedings of the IEEE In-
* ternational Conference on Intelligent Robots and Systems (IROS), pages
* 2743–2748, Las Vegas, USA, October 2003.
*
* \author James Crosby
*/
// 2D-NDT点云配准
template <typename PointSource, typename PointTarget>
class NormalDistributionsTransform2D : public Registration<PointSource, PointTarget>
{
using PointCloudSource = typename Registration<PointSource, PointTarget>::PointCloudSource;
using PointCloudSourcePtr = typename PointCloudSource::Ptr;
using PointCloudSourceConstPtr = typename PointCloudSource::ConstPtr;
using PointCloudTarget = typename Registration<PointSource, PointTarget>::PointCloudTarget;
using PointIndicesPtr = PointIndices::Ptr;
using PointIndicesConstPtr = PointIndices::ConstPtr;
public:
using Ptr = shared_ptr< NormalDistributionsTransform2D<PointSource, PointTarget> >;
using ConstPtr = shared_ptr< const NormalDistributionsTransform2D<PointSource, PointTarget> >;
/** \brief Empty constructor. */
// 空的构造函数
NormalDistributionsTransform2D ()
: Registration<PointSource,PointTarget> (),
grid_centre_ (0,0), grid_step_ (1,1), grid_extent_ (20,20), newton_lambda_ (1,1,1)
{
reg_name_ = "NormalDistributionsTransform2D";
}
/** \brief Empty destructor */
~NormalDistributionsTransform2D () {}
/** \brief centre of the ndt grid (target coordinate system)
* \param centre value to set
*/
// 设置NDT网格中心, 目标坐标系的, (也就是要将点云匹配过去的坐标系)
virtual void
setGridCentre (const Eigen::Vector2f& centre) { grid_centre_ = centre; }
/** \brief Grid spacing (step) of the NDT grid
* \param[in] step value to set
*/
// 步长设置
virtual void
setGridStep (const Eigen::Vector2f& step) { grid_step_ = step; }
/** \brief NDT Grid extent (in either direction from the grid centre)
* \param[in] extent value to set
*/
// 从网格中心扩展多少,也就是NDT cell范围?
virtual void
setGridExtent (const Eigen::Vector2f& extent) { grid_extent_ = extent; }
/** \brief NDT Newton optimisation step size parameter
* \param[in] lambda step size: 1 is simple newton optimisation, smaller values may improve convergence
*/
// 设置优化步长, 1是简单的牛顿迭代, 更小的值可以提高收敛效果
virtual void
setOptimizationStepSize (const double& lambda) { newton_lambda_ = Eigen::Vector3d (lambda, lambda, lambda); }
/** \brief NDT Newton optimisation step size parameter
* \param[in] lambda step size: (1,1,1) is simple newton optimisation,
* smaller values may improve convergence, or elements may be set to
* zero to prevent optimisation over some parameters
*
* This overload allows control of updates to the individual (x, y,
* theta) free parameters in the optimisation. If, for example, theta is
* believed to be close to the correct value a small value of lambda[2]
* should be used.
*/
// 重载函数, 就是说,当认为优化的时候某个变量如朝向角已经足够精确了,那么可以把 lambda[2]设置为一个小值,加快速度
virtual void
setOptimizationStepSize (const Eigen::Vector3d& lambda) { newton_lambda_ = lambda; }
protected:
/** \brief Rigid transformation computation method with initial guess.
* \param[out] output the transformed input point cloud dataset using the rigid transformation found
* \param[in] guess the initial guess of the transformation to compute
*/
// 使用初始位姿计算点云之间的变换矩阵,输出: 利用变换将输入点云匹配到目标点云
void
computeTransformation (PointCloudSource &output, const Eigen::Matrix4f &guess) override;
using Registration<PointSource, PointTarget>::reg_name_;
using Registration<PointSource, PointTarget>::target_;
using Registration<PointSource, PointTarget>::converged_;
using Registration<PointSource, PointTarget>::nr_iterations_;
using Registration<PointSource, PointTarget>::max_iterations_;
using Registration<PointSource, PointTarget>::transformation_epsilon_;
using Registration<PointSource, PointTarget>::transformation_rotation_epsilon_;
using Registration<PointSource, PointTarget>::transformation_;
using Registration<PointSource, PointTarget>::previous_transformation_;
using Registration<PointSource, PointTarget>::final_transformation_;
using Registration<PointSource, PointTarget>::update_visualizer_;
using Registration<PointSource, PointTarget>::indices_;
Eigen::Vector2f grid_centre_;
Eigen::Vector2f grid_step_;
Eigen::Vector2f grid_extent_;
Eigen::Vector3d newton_lambda_;
public:
PCL_MAKE_ALIGNED_OPERATOR_NEW
};
} // namespace pcl
ndt_2d.hpp
1 |
|