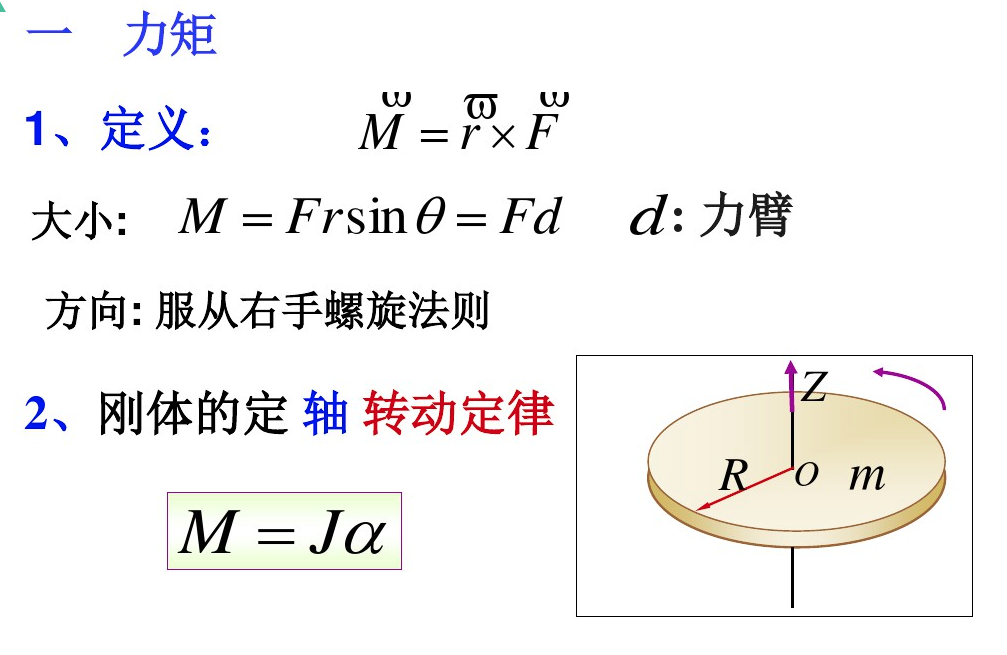
车辆动力学模型
变量约定
| 变量名 | 意义 | 变量名 | 意义 |
|---|---|---|---|
| \(F_y\) | 整车受到y方向的力 | \(\delta\) | 方向盘转角 |
| \(F_{yf}\) | 前轮胎受到y方向的力 | \(\delta_f\) | 前轮转角 |
| \(F_{yr}\) | 后轮胎受到y方向的力 | \(\delta_r\) | 后轮转角 |
| \(V_x\) | 纵向速度 | \(\delta_o\) | 外轮转向角 |
| \(V\) | 全速度 | \(\delta_i\) | 内轮转向角 |
| \(\dot{y}\) | 横向速度 | \(l_w\) | 宽度 |
| \(V_{y}\) | 横向速度,等于\(\dot{y}\) | \(\alpha_f\) | 前轮胎滑移角 |
| $m $ | 质量 | \(\alpha_r\) | 后轮胎滑移角 |
| \(I_z\) | Z轴转动惯量 | \(C_\alpha\) | 轮胎转向刚度 |
| \(l_f\) | 前悬长度 | \(F_z\) | 轮胎法向力 |
| \(l_r\) | 后悬长度 | \(\mu\) | 摩擦系数 |
| \(L\) | \(L=l_f+l_r\) | \(\dot{\psi}_{des}\) | 期望的偏航角速度 |
| \(\psi\) | 偏航角 | \(\beta\) | 在车辆重心处的滑动角度 |
| \(\dot{\psi}\) | 偏航角速度 | \(\theta_v\) | 速度方向与纵轴的角速度 |
| \(r\) | 偏航角速度\(r=\dot{\psi}\) | \(\phi\) | road bank angle |
| \(X,Y\) | 轴 | \(R\) | 转弯半径 |
| \(e_1\) | 相对于路面的横向位置误差 | ||
| \(e_2\) | 相对于路面的偏航角误差 | ||
| \(C(t)\) | 菲涅耳积分(Fresnel Integral) | ||
| \(S(t)\) | 菲涅耳积分(Fresnel Integral) |
车辆横向运动的运动学模型
运动学模型提供了车辆运动的数学描述,而不考虑影响运动的力。运动方程完全是基于支配系统的几何关系。
考虑一个单车模型
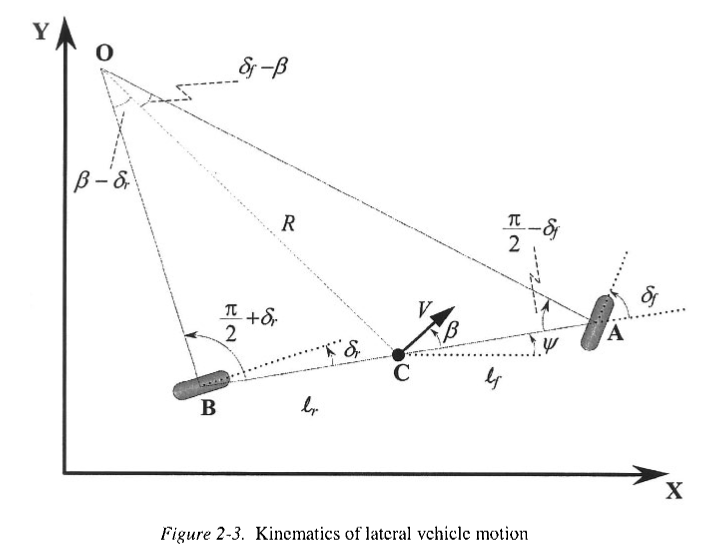
表示前轮和后轮的转向角分别为\(\delta_f\)和\(\delta_r\),该模型是在假定前轮和后轮都可以操纵的情况。对于只有前轮可以操纵的情况,那么有\(\delta_r=0\)。整车质心在点C,从前轮胎A到质心点C的距离为\(l_f\),后轮胎到点C为\(l_r\),其中\(L=l_f+l_r\)。
假设车辆具有平面运动,则可以使用\((X,Y,\psi)\)来描述。整车速度使用向量\(V\)来描述,与车辆的纵轴成一个角度\(\beta\),其中,\(\beta\)称为车的侧滑角度。
假设
运动学模型建立的主要假设是:点A和点B的速度矢量分别与前轮和后轮的方向一致,换句话说,就是前轮胎的速度向量与纵轴方向成\(\delta_f\)的角,后轮的速度向量与纵轴方向成\(\delta_r\)的角。这相当于假设两个轮子的“滑动角度”为零 (?不懂) 。 这是一个合理的假设为低速运动的车辆(例如,速度低于5米/秒),这是因为在低速时,轮胎产生的侧向力很小。
为了在半径为R的环形路上行驶,两个轮胎的总侧向力为:
\[ \begin{aligned} \frac{mV^2}{R} \end{aligned} \]
当速度很小时,侧向力很小。当侧向力很小时,如2.4节后面所解释的那样,假设每个轮子上的速度矢量都在轮子的方向上确实是非常合理的。
车辆路径R的半径即为由连接重心C到瞬时旋转中心O的直线OC的长度。车辆速度与直线OC垂直,速度方向相对于车辆纵轴方向称为滑移角\(\beta\)。
车辆的朝向角为\(\psi\),于是有\(\gamma=\psi+\beta\)
对三角形\(OCA\)使用正弦定理:
\[ \begin{aligned} \frac{\sin(\delta_f-\beta)}{l_f} &= \frac{\sin(\frac{\pi}{2}-\delta_f)}{R} \\ \frac{\sin(\delta_f)\cos(\beta)-\sin(\beta)\cos(\delta_f)}{l_f} &= \frac{\cos(\delta_f)}{R} \end{aligned} \tag{2.5} \]
对三角形\(OCB\)使用正弦定理
\[ \begin{aligned} \frac{\sin(\beta-\delta_r)}{l_r} &= \frac{\sin(\frac{\pi}{2}+\delta_r)}{R} \\ \frac{\cos(\delta_r)\sin(\beta)-\cos(\beta)\sin(\delta_r)}{l_r} &= \frac{\cos(\delta_r)}{R} \end{aligned} \tag{2.6} \]
两式分别乘以\(\frac{l_f}{\cos(\delta_f)}\)和\(\frac{l_r}{\cos(\delta_r)}\),分别得到
\[ \tan(\delta_f)\cos(\beta)-\sin(\beta)=\frac{l_f}{R} \]
\[ \tan(\beta)-\tan(\delta_r)\cos(\beta)=\frac{l_r}{R} \]
两式相加,得到
\[ [\tan(\delta_f)-\tan(\delta_r)]\cos(\beta)=\frac{l_f+l_r}{R} \tag{2.8} \]
如果我们假设车辆路径的半径由于车速较低而变化缓慢,那么车辆的方向变化率(\(\psi\))一定等于车辆的角速度,由车辆角速度等于\(\frac{V}{R}\),于是有:
\[ \dot{\psi}=\frac{V}{R} \]
于是,替换变量\(R\),重写式2.8
\[ \dot{\psi}=\frac{V\cos(\beta)}{l_f+l_r}(\tan(\delta_f)-\tan(\delta_r)) \tag{2.12} \]
得到的模型,有三个输入\(\delta_f,\delta_r,V\),速度V是一个外部变量,可以假设为一个时变函数,也可以从纵向车辆模型中得到。
通过将式2.5乘以\(l_r\),对式2.6乘以\(l_f\),两式相减,可以得到侧滑角\(\beta\):
\[ \beta=\tan^{-1} \frac{l_f \tan \delta_r + l_r \tan \delta_f}{l_f+l_r} \]
阿克曼转向
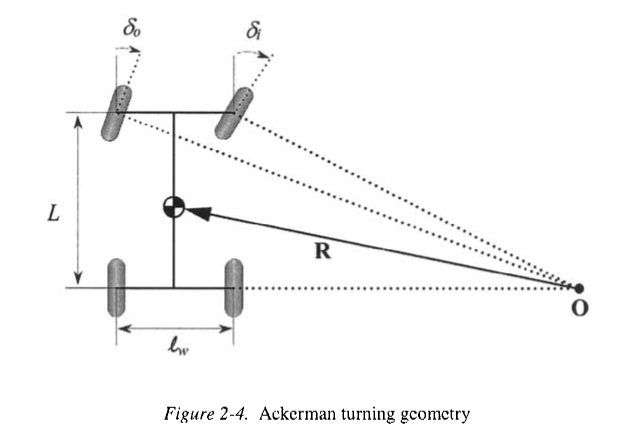
令\(l_w\)为宽度,\(\delta_o\)和\(\delta_i\)分别为前轮的外轮和内轮的转角。并且假设\(L=l_f+l_r << R\),并且侧滑角\(\beta\)很小 \((\cos \beta) \approx 1\),那么式2.12可以近似为:
\[ \begin{aligned} & \psi=\frac{V}{R}=\frac{V \delta}{L} \\ & \Longrightarrow \frac{\dot{\psi}}{V} \approx \frac{1}{R} = \frac{\delta}{L} \\ &\Longrightarrow \delta = \frac{L}{R} \end{aligned} \]
又因为内外车轮的行驶路径曲率是不同的,于是有
\[ \delta_o=\frac{L}{R+\frac{l_w}{2}} \]
\[ \delta_i=\frac{L}{R-\frac{l_w}{2}} \]
前轮平均转向角约为:
\[ \delta=\frac{\delta_o+\delta_i}{2} \approx \frac{L}{R} \]
其中,差为
\[ \delta_i-\delta_o =\frac{L}{R^2}l_w =\delta^2 \frac{l_w}{L} \]
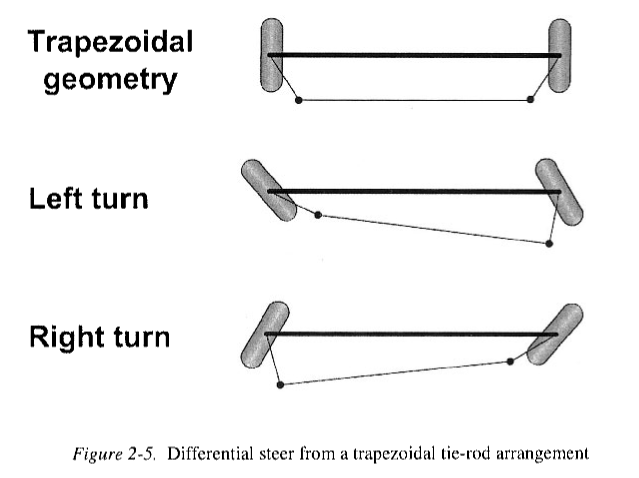
因此,两个前轮转角的差值与平均转角的平方成正比,这种差动转向可以从梯形拉杆装置中获得,从图中可以看出,无论是左转还是右转,内转轮的转向角度都比较大。
总结
| 符号 | 意义 | 等式 |
|---|---|---|
| X | 全局坐标系X坐标轴 | \(\dot{X}=V\cos(\psi+\beta)\) |
| Y | 全局Y轴 | \(\dot{Y}=V\sin(\psi+\beta)\) |
| \(\psi\) | 朝向角:车体纵轴与X轴的夹角 | \(\dot{\psi}=\frac{V\cos(\beta)}{l_f+l_r}(\tan(\delta_f)-\tan(\delta_r))\) |
| \(\beta\) | 侧滑角 | \(\beta=\tan^{-1} \frac{l_f \tan \delta_r + l_r \tan \delta_f}{l_f+l_r}\) |
车辆动力学模型
在较高的车辆速度下,不能再假设每个轮子上的速度是在轮子的方向上。在这种情况下,必须建立横向车辆运动的动态模型,而不是运动学模型。
考虑具有两个自由度的车辆的“自行车”模型,如图2-6所示
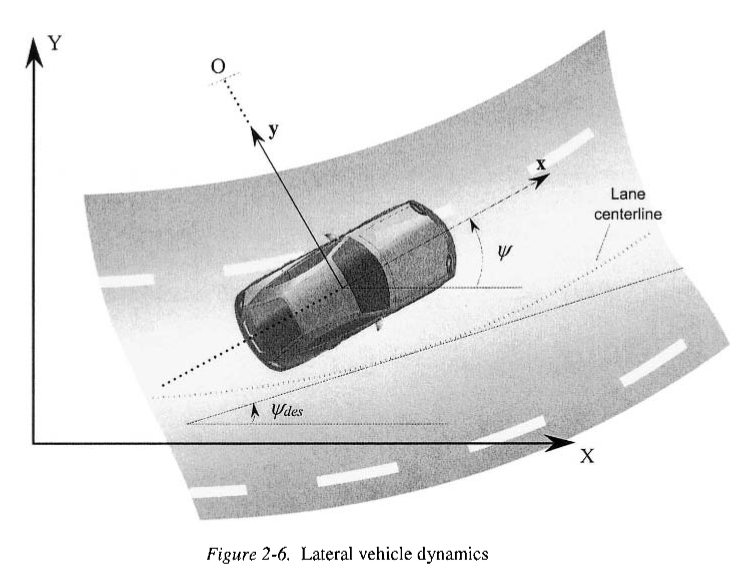
两个自由度分别是横向位置\(y\)和车辆的偏航角\(\psi\)。车辆的横向位置是沿着车辆的横向轴测量到0点,即车辆的旋转中心,车辆的偏航角\(\psi\)是根据全局X轴来测量的,车辆在c.g.处的纵向速度用\(V_x\)表示。
这里暂时不讨论道路的倾斜角。然后应用牛顿第二定律:
\[ ma_y=F_{yf}+F_{yr} \tag{2.19} \]
其中,\(a_y=\frac{d^2}{d t^2}_{inertial}\)是车辆的在\(y\)轴方向的惯性加速度,\(F_{yf},F_{yr}\)分别是前轮胎和后轮胎的横向力,这两项对\(y\)轴方向的惯性加速度产生贡献,即加速度\(\ddot{y}\)是由\(y\)轴方向的运动和向心加速度\(V_x \dot{\psi}\)产生的,因此有:
\[ a_y=\ddot{y}+V_x \dot{\psi} \tag{2.20} \]
同时,将式2.19代入2.20,车辆横向平动运动方程为:
\[ m(\ddot{y}+V_x \dot{\psi})=F_{yf}+F_{fr} \tag{2.21} \]
关于z轴的力矩平衡得到了偏航动力学方程:
\[ l_z \ddot{\psi}=l_f F_{yf}-l_r F_{yr} \tag{2.22} \]
补充材料: 力矩与转动惯量
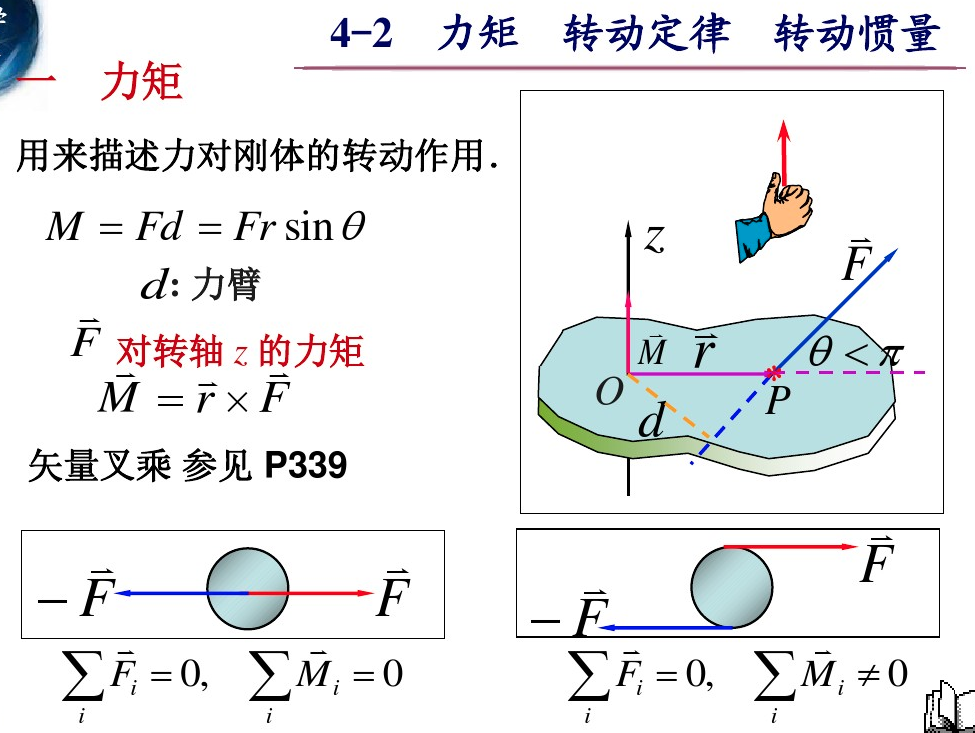
从补充材料可知,上面的等式只是从向量的模来考虑。
下一步是对作用于车辆轮胎的横向力\(F_{yf},F_{yr}\)进行建模。试验结果表明,在小滑角情况下,轮胎的侧向力(横向力)与滑角成正比。轮胎的滑移角定义为轮胎方向与车轮速度矢量方向之间的夹角,如图2.7
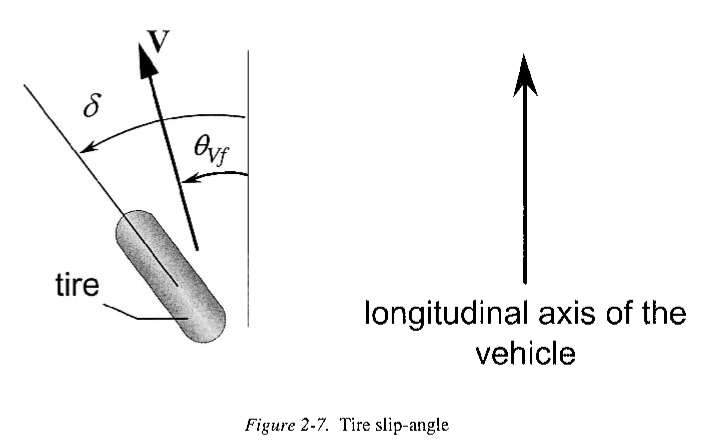
如图所示,前轮的滑移角为:
\[ \alpha_f=\delta-\theta_{vf} \tag{2.23} \]
其中,\(\theta_{vf}\)是速度矢量与车辆纵轴的夹角,\(\delta\)是前轮与纵轴的夹角。同样的,后轮的滑移角近似为:
\[ \alpha_r=-\theta_{vr} \tag{2.24} \]
这里暂不解释为什么会有滑移角的存在,具体可见
接下来,前轮受到的横向力可以写成:
\[ F_{yf}=2C_{\alpha f}(\delta-\theta_{vf}) \]
其中,常数\(C_{\alpha f}\)称为前轮的转向刚度,\(\theta_{vf}\)是前轮速度矢量与车辆纵轴的夹角,\(\delta\)是前轮与纵轴的夹角。有一个系数2是因为有两个前轮。
相似的,后轮的轮胎横向力可以写成:
\[ F_{yr}=2C_{\alpha r}(-\theta_{vr}) \]
其中,\(C_{\alpha r}\)是前轮的转向刚度,\(\theta_{vr}\)是后轮速度矢量与车辆纵轴的夹角。
于是有:(怎么来的没说)
\[ \tan(\theta_{vf})=\frac{V_y+l_f \dot{\psi}}{V_x} \tag{2.29} \]
\[ \tan(\theta_{vr})=\frac{V_y-l_r \dot{\psi}}{V_x} \tag{2.30} \]
使用小角度近似,\(\tan(x)=x\),有:
\[ (\theta_{vf})=\frac{\dot{y}+l_f \dot{\psi}}{V_x} \]
\[ (\theta_{vr})=\frac{\dot{y}-l_r \dot{\psi}}{V_x} \]
将式2.23、2.24、2.29、2.30代入2.21和2.22,可以得到状态空间模型:
\[ \begin{aligned} \frac{d}{dt} \begin{bmatrix} y \\ \dot{y} \\ \psi \\ \dot{\psi} \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & -\frac{2C_{\alpha_f}+2C_{\alpha_r}}{mV_x} & 0 & -V_x-\frac{2C_{\alpha_f} l_f-2C_{\alpha_r}l_r}{mV_x} \\ 0 & 0 & 0 & 1 \\ 0 & -\frac{2C_{\alpha_f} l_f-2C_{\alpha_r}l_r}{I_z V_x} & 0 & -\frac{2 l_f^2 C_{\alpha_f}+2l_r^2 C_{\alpha_r}}{mV_x} \end{bmatrix} \begin{bmatrix} y \\ \dot{y} \\ \psi \\ \dot{\psi} \end{bmatrix} + \begin{bmatrix} 0 \\ \frac{2C_{\alpha f}}{m} \\ 0 \\ \frac{2 l_f C_{\alpha f}}{I_z} \end{bmatrix} \delta \end{aligned} \]