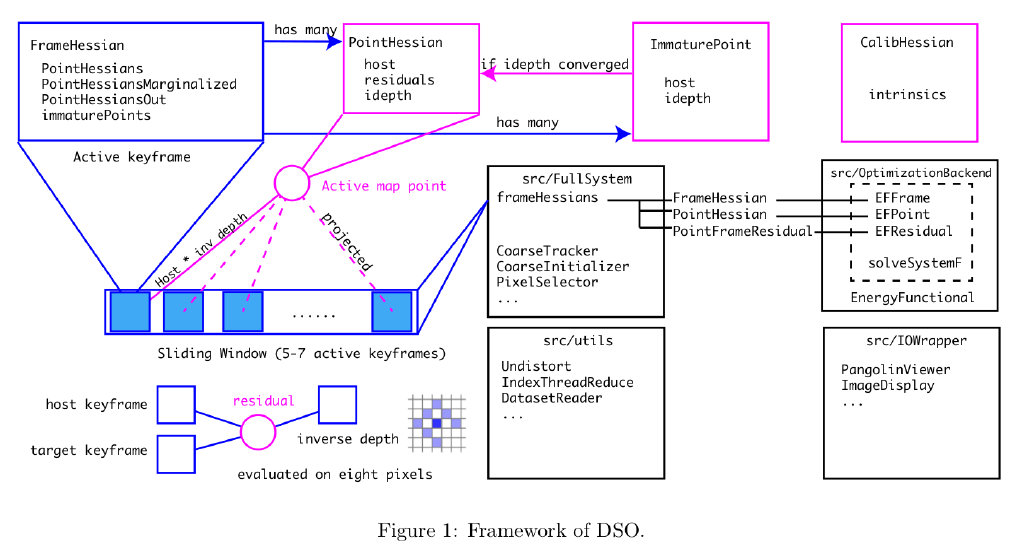
1. DSO-1-系统框架与初始化


2. 直接&稀疏
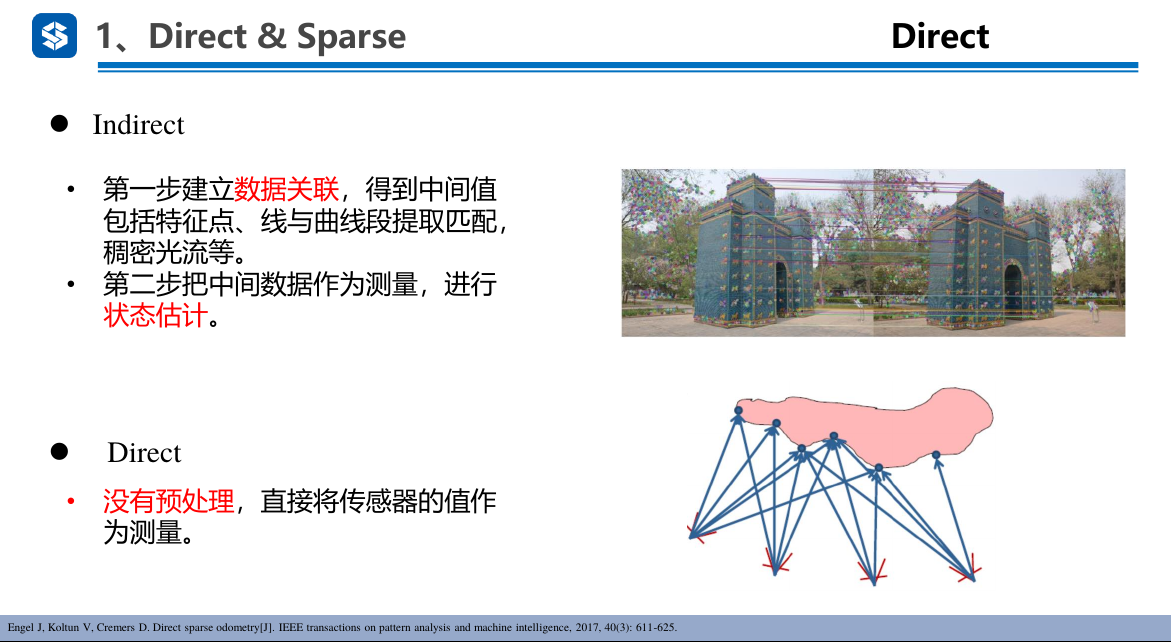
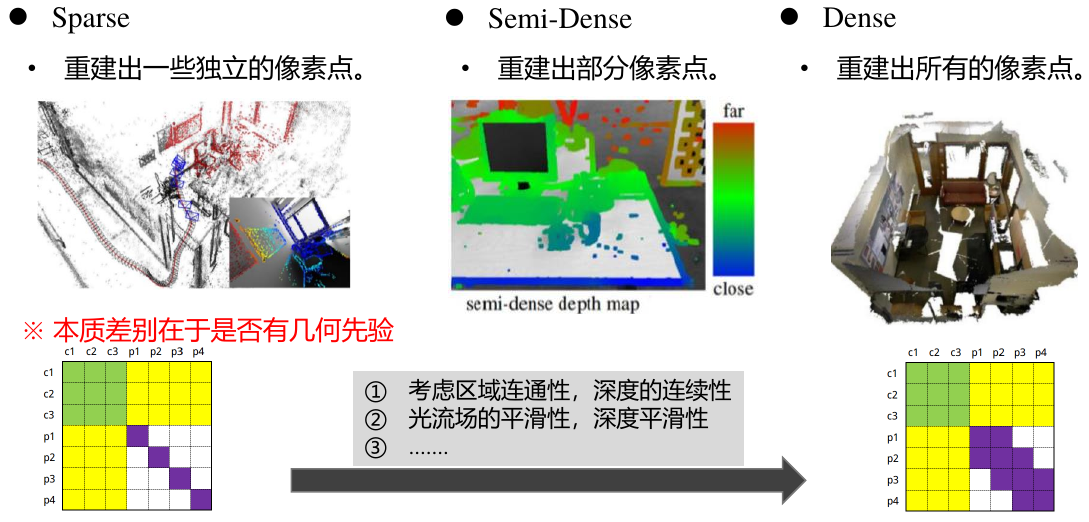
- 非直接法: ORB_SLAM2
- 直接法: DSO
3. 相机几何模型与光度模型&雅克比推导
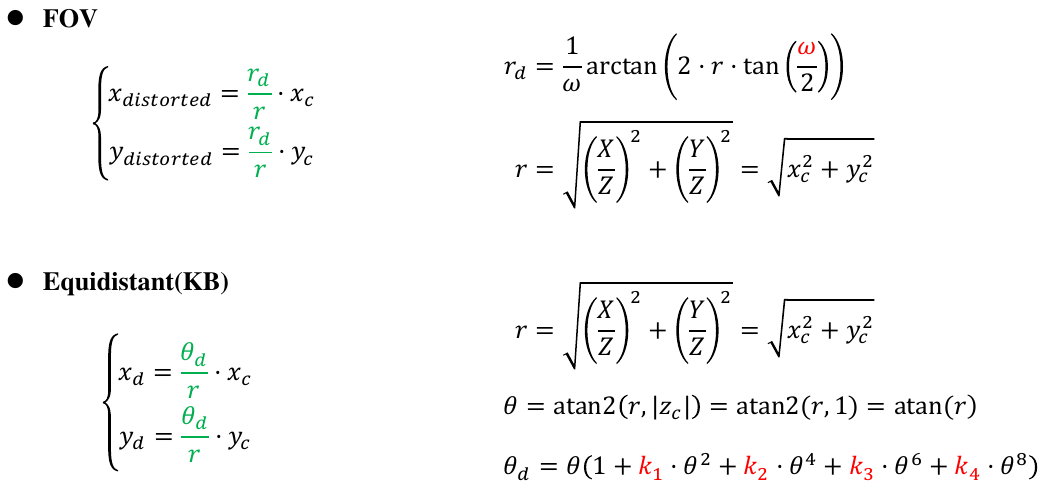

DSO中的几种畸变模型:
- FOV: (\(f_x,f_y,c_x,c_y,\omega\) 一共5个参数)
- RadTan: 考虑径向和切向两种畸变(视觉SLAM14讲第二版P102)
- KB: \(f_x,f_y,c_x,c_y,k_1,k_2,k_3,k_4\) 一共8个参数
3.1. 计算去畸变后的新内参


(1)已知相机内参和畸变模型, 给定一个超大范围的归一化平面[x_min->x_max],[y_min->y_max], 遍历这个归一化平面上的点
- 遍历归一化平面上的点,将每个点应用畸变模型+相机模型,得到畸变的像素点(也就是相机输出图像上的点)
- 不断裁剪这个超大范围的归一化平面,直到这个归一化平面[x_min->x_max],[y_min->y_max]的边界范围内所有(任意)点所对应的畸变像素点都在畸变图像(相机输出图像)的范围内
(2)取归一化平面上的边界,4个点(\(X_{min},X_{max},Y_{min},Y_{max}\)组合得到),即可计算出新的(无畸变的)相机内参
(虽然新的参数还不知道,但是这里这是先用符号表示)
\[ \left \{ \begin{aligned} u_{min}=f_x' X_{min}+c_x' \\ u_{max}=f_x' X_{max}+c_x' \end{aligned} \Longrightarrow \underbrace{u_{max}-u_{min}}_{known}=f_x' \underbrace{(X_{max}-X_{min})}_{known} \right . \]
因此,可得
\[ f_x'=\frac{u_{max}-u_{min}}{X_{max}-X_{min}} \]
令\(u_{min}=0\),代入\(u_{min}=f_x' X_{min}+c_x'\),可得
\[ c_x'= - f_x' X_{min} \]
(3)对于y方向的新内参,同理
根据这些新的(无畸变的)相机内参,如何从畸变图像得到无畸变图像?
畸变图像----->旧相机内参------>归一化平面
归一化平面---->新相机内参------>无畸变图像
3.2. 光度模型
3.2.1. 辐射(与方向有关),\(B_i(x)\)
辐射率(Radiance)是指一个表面在单位立体角和单位投影面积上所发射、反射、透射或接收的辐射通量
3.2.2. 辐照(与方向无关),IR(x)
在辐射测量学中,辐照度是指一个表面单位面积所接受的辐射通量(功率),和方向无关。比如,用来描述传感器像元的入射光强(来自于不同方向的环境光的累加)。
3.2.3. 渐晕,V(x)
光学晕影是由一个或多个透镜的实际尺寸造成的,后方的元件遮蔽了前方的,导致前端透镜离轴的有效入射光减少,结果是光的强度由图像中心向周围逐渐减弱。
也就是说,假如拍摄一个亮度非常均匀的物体,图像中心和边缘的亮度值并不一致。
3.2.4. 三者关系
\[ IR(x)=V(x)B_i(x) \]
3.2.5. 快门
快门影响的是曝光时间。自动曝光模式下,不同场景曝光时间并不一样,会导致同一物体在不同场景下的灰度值产生差异。另外还想提到的是全局快门(global shutter)和卷帘快门(rolling shutter)。
- 全局快门保证所有感光元件的曝光起始时间和间隔是一样的
- 卷帘快门并不能保证。
- 因此文献中一般推荐使用全局快门。
3.2.6. 响应函数
传感器(CCD/CMOS)将每个像元接收到的光子通过一系列处理转化为亮度值。这里面涉及到光电效应、ADC、DSP等过程。输入的曝光量和输出的亮度值之间的关系称为响应函数(response function)。
响应函数一般来说是非线性的,甚至包含人为调整的成分,比如伽马校正、白平衡、色调、饱和度等。
为图像进行伽马编码的目的是用来对人类视觉的特性进行补偿,从而根据人类对光线或者黑白的感知,最大化地利用表示黑白的数据位或带宽。人眼对暗部比较敏感,因此一般选择提高暗部的分辨率。这些因素会非线性地修正曝光量,因此作者希望通过光度标定来补偿它们的影响。
3.2.7. 光度模型
结合了曝光时间和响应函数[映射到0-255],(在光照时间ti内对辐照积分,再传入响应函数)
\[ I_i(x)=G(t_i IR(x))=G(t_i V(x)B_i(x)) \]
- 这里的I_i(x)可否理解为就是图像上的强度?
3.2.8. 光度矫正
3.2.8.1. 方法一:
- 标定响应函数G()
- 标定晕影V(x)
通过标定V和G,可以反求出辐射B,(使用B去做直接法当然要比I准确地多。当然,场景的亮度在不同视角下有差异,这是无法避免的)
\[ I_i'(x)= t_i B_i(x) = \frac{G^{-1}(I_i(x))}{V(x)} \]
- 上面得到的\(I_i'(x)\)就是经过矫正之后的光度,仅包含曝光时间和辐射,其中曝光时间在每一帧可能都不一样,因此不是常数。
3.2.8.2. 方法二:
对于做过光度标定的相机,我们可以用上面的方法一处理,对于一般的相机呢? 通常采用下面的光度仿射变换进行矫正
\[ I_i'(x)=e^{-\alpha_i}(I_i(x)-b_i) \]
总结如下:

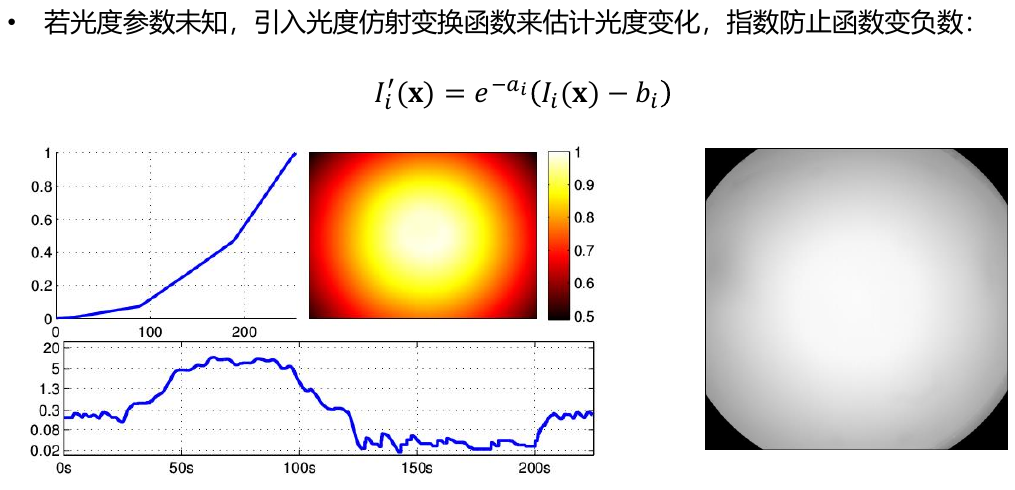
光度模型对于直接法来说是十分重要的,因为直接法是基于光度不变性的假设
3.3. 光度误差模型
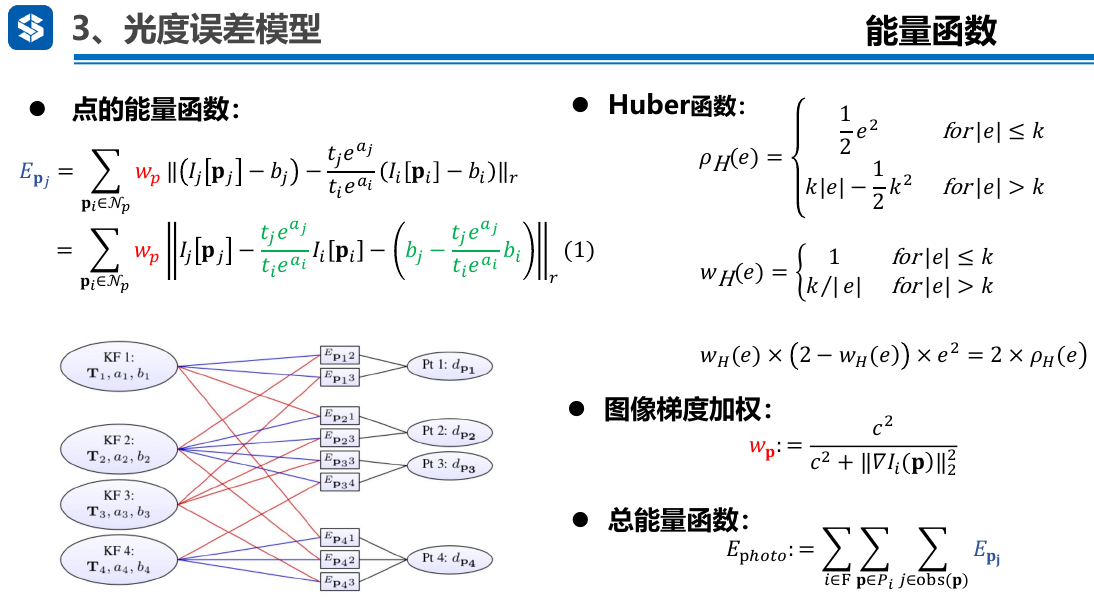
- 上面能量函数中: \(I[p_j] ...\)指的是经过矫正之后的光度
- 图像梯度加权:对于边缘处非连续的点,一旦发生移动,那么其光度变化会很大,因此如果引入了外点,会造成明显的影响,因此对于梯度较大的点,那么其权重一般较小。
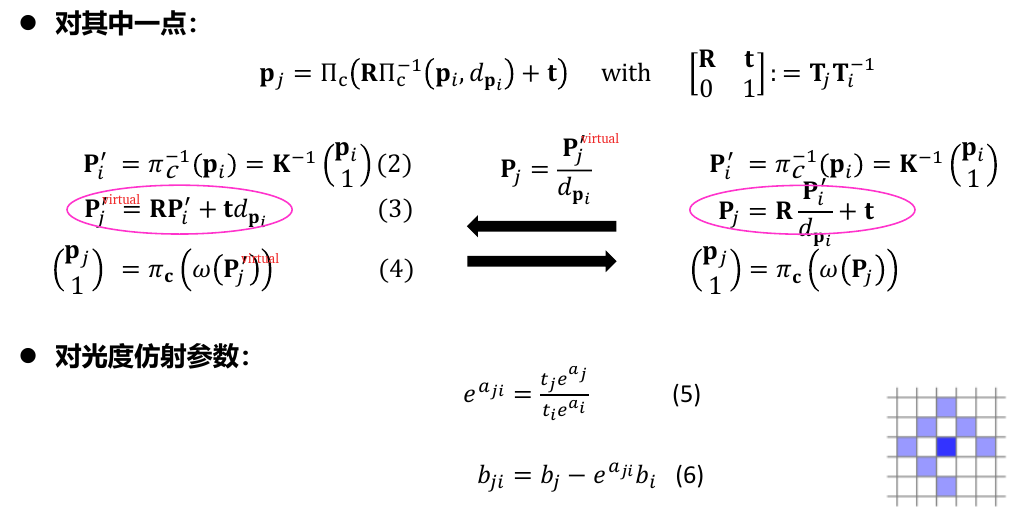
假设世界坐标系中有某点P,其对于两帧图像上的点为\(x_i,x_j\),有
第i帧归一化平面上的点\(P_i'\)
\[ P_i'=\pi_c^{-1}(p_i)=K^{-1} \begin{pmatrix} x_i \\ 1 \end{pmatrix} \]
其中,第i帧相机坐标系上的点\(P_i=\frac{P_i'}{d_{pi}}\) , \(d_{pi}=\frac{1}{Z_i}\)为逆深度
第j帧相机坐标系上的点\(P_j\)
\[ P_j=R P_i + t= R\frac{P_i'}{d_{pi}}+t \]
对上式两边同时乘以第i帧点\(P_i\)的逆深度,得到一个(齐次点)虚拟点\(P_j^{virtual}\)
\[ \begin{aligned} P_j d_{pi} &= R P_i' + t d_{pi} \\ P_j^{virtual} &= R P_i' + t d_{pi} \end{aligned} \]
那么,第i帧相机坐标系点\(P_i\)转换到第j帧相机坐标系的点\(P_j\)可以如下表示:
\[ P_j=\frac{P_j^{virtual}}{d_{pi}} \]
\[ \Longrightarrow P_j[2]=\frac{P_j^{virtual}[2]}{d_{pi}} \]
最终,第j帧相机坐标系点\(P_j\)投影到图像上的点\(x_j\)可表示为:
\[ \begin{aligned} \begin{pmatrix} x_j \\ 1 \end{pmatrix} =\pi_c(P_j') &= \pi_c(\frac{P_j}{P_j[2]}) \\ &= \pi_c(\frac{P_j^{virtual}}{d_{pi} \cdot P_j[2]}) \\ &= \pi_c(\frac{P_j d_{pi}}{P_j^{virtual}[2]}) \end{aligned} \]
上式子的\(\frac{d_{pi}}{P_j^{virtual}[2]}\)对应DSO代码中ResidualProjections.h文件的new_idepth = idepth*drescale;这一句。
1 | EIGEN_STRONG_INLINE bool projectPoint( |
3.4. 关于(齐次点)虚拟点\(P_j^{virtual}\)的意义
到这里,是时候讨论\(P_j^{virtual}\)的内在意义了:
- 已知将点Pi从第i帧相机坐标系转换到第j帧相机坐标系的坐标q如下:
\[ q=P_j=R P_i + t= R\frac{P_i'}{d_{pi}}+t \]
- 对q转换到归一化平面上,即得到\(P_j'\)
\[ \begin{aligned} P_j'= \begin{bmatrix} \frac{P_j[0]}{P_j[2]} \\ \frac{P_j[1]}{P_j[2]} \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{q[0]}{q[2]} \\ \frac{q[1]}{q[2]} \\ 1 \end{bmatrix} \end{aligned} \]
- 同时,有虚拟点\(P_j^{virtual}\) , (\(P_i'\)为点\(P_i\)的归一化平面点)
\[ P_j^{virtual}= d_{pi} P_j = R P_i' + t d_{pi} \]
对虚拟点\(P_j^{virtual}\)也转换到归一化平面上
\[ \begin{aligned} P_j^{virtual-normal}= \begin{bmatrix} \frac{d_{pi} P_j[0]}{d_{pi} P_j[2]} \\ \frac{d_{pi} P_j[1]}{d_{pi} P_j[2]} \\ 1 \end{bmatrix}= \begin{bmatrix} \frac{P_j[0]}{P_j[2]} \\ \frac{P_j[1]}{P_j[2]} \\ 1 \end{bmatrix} \end{aligned} \]
(4)可以看到,归一化之后的虚拟点\(P_j^{virtual-normal}\)与归一化之后的真实点\(P_j'\)是等价的。
DSO作者采用(齐次点)\(P_j^{virtual}\)的目的是希望可以简化下面的雅克比求导过程。
3.5. 雅克比
3.5.1. 损失函数(残差)

上面的残差怎么来的,其实原式如下:
\[ \begin{aligned} E_{pj}=\sum_{p_i \in \mathcal{N}_p} w_p || \frac{1}{t_j \exp^{\alpha_j}}(I_j[p_j]-b_j)-\frac{1}{t_i \exp^{\alpha_i}}(I_j[p_i]-b_i)||_r \end{aligned} \]
其中,\(t_k\)是光度矫正,\(\exp^{\alpha}\)是光度仿射变换

3.5.2. 对光度参数\(a_{ji},b_{ji}\)求导

3.5.3. 对相对位姿求导,即\(\frac{\partial e}{\partial \delta \xi}\)
这个图的雅克比计算是基于DSO作者所使用的(齐次点)\(P_j^{virtual}\)进行的,可以简化的雅克比求导过程。

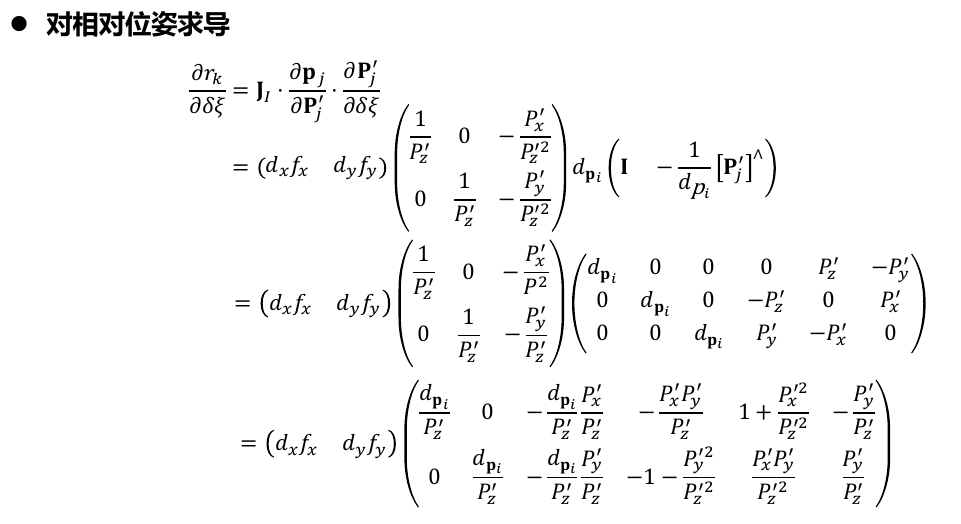
下面给出先使用正常思路进行推导雅克比,在最后证明两种方法的推导结果是一致的:
对于求相对位姿的雅克比,可以对残差作一些简化:
\[ \begin{aligned} r_k &= \frac{1}{t_j \exp^{\alpha_j}}(I_j[p_j]-b_j)-\frac{1}{t_i \exp^{\alpha_i}}(I_i[p_i]-b_i) \\ & \Longrightarrow r_k = I_j[p_j]-I_i[p_i] \\ & \Longrightarrow r_k = I_1[u]-I_2[p_i] \end{aligned} \]
其中, q为第i帧相机坐标系点\(P_i\)转换到第j帧相机坐标系的点,u为对应的图像平面点
\[ \begin{aligned} q=P_j=TP_i \\ u=x_j=\frac{1}{q[2]} K q \end{aligned} \]
现在,回到一个问题: 问什么需要求雅克比?
目标:最小化损失函数\(r_k\),需要优化的参数有:
- 光度参数\(a_{ji},b_{ji}\)
- 从第i帧到第j帧的变换(\(T_{j\leftarrow i}\))
- 第i帧的3D点的位置(或者说第i帧3D点的逆深度\(d_{pi}\))
推导开始:
(1)考虑高斯牛顿法,对损失函数原函数进行泰勒一阶展开
\[ f(x+\Delta x)=f(x)+J^T(x)\Delta x \]
即, 把\(\Delta x\)看做是姿态的扰动量\(\delta \xi\), 得到:
\[ \begin{aligned} e(\xi \oplus \delta \xi) &= I_1(\frac{1}{Z_j}K \exp(\delta \xi ^\wedge)\exp(\xi^\wedge)P_i)-I_2(\frac{1}{Z_i}KP_i) \\ &= I_1(\frac{1}{Z_j}K (1+\delta \xi ^\wedge)\exp(\xi^\wedge)P_i)-I_2(\frac{1}{Z_i}KP_i) \\ &= I_1(\frac{1}{Z_j}K \exp(\xi^\wedge)P_i+ \underbrace{\frac{1}{Z_j}K(\delta \xi ^\wedge)\exp(\xi^\wedge)P_i}_{u})-I_2(\frac{1}{Z_i}KP_i) \end{aligned} \]
对上式在\(\delta \xi \approx 0\)处进行泰勒一阶展开,可以得到
\[ \begin{aligned} e(\xi \oplus \delta \xi) &= I_1(\frac{1}{Z_j}K \exp(\xi^\wedge)P_i+ \underbrace{\frac{1}{Z_j}K(\delta \xi ^\wedge)\exp(\xi^\wedge)P_i}_{u})-I_2(\frac{1}{Z_i}KP_i) \\ &\approx I_1(\frac{1}{Z_j}K \exp(\xi^\wedge)P_i)+\frac{\partial I_1(\frac{1}{Z_j}K \exp(\xi^\wedge)P_i+ \frac{1}{Z_j}K(\delta \xi ^\wedge)\exp(\xi^\wedge)P_i)}{\partial \delta \xi} \delta \xi -I_2(\frac{1}{Z_i}KP_i) \\ &= I_1[u]+J^T\delta \xi-I_2[p_i] \end{aligned} \]
其中,J为雅克比,实际上就是\(I_1(u)\)对位姿量的偏导
(2)\(I_1(u)\)对位姿量的偏导
\[ \begin{aligned} J^T=\frac{\partial e}{\partial T}=\frac{\partial I_1(u)}{\partial \delta \xi} &=\frac{\partial I_1}{\partial u} \frac{\partial u}{\partial q} \frac{\partial q}{\partial \delta \xi} \end{aligned} \]
其中,
- \(\frac{\partial I_1}{\partial u}\)为在点u处的图像像素梯度
\[ \frac{\partial I_1}{\partial u}=\frac{\partial I_1}{\partial x_j}= \begin{pmatrix} \frac{\partial I_j}{\partial u_j } & \frac{\partial I_j}{\partial v_j} \end{pmatrix} =(d_x,d_y) \]
\(\frac{\partial u}{\partial q}\)为相机投影方程关于相机坐标系下的三维点\(q\)的导数
(点\(q=[X,Y,Z]^T=(q[0],q[1],q[2])^T\)为第i帧相机坐标系点\(P_i\)转换到第j帧相机坐标系的点)
\[ \frac{\partial u}{\partial q}= \begin{bmatrix} \frac{\partial u}{\partial X} & \frac{\partial u}{\partial Y} & \frac{\partial u}{\partial Z} \\ \frac{\partial v}{\partial X} & \frac{\partial v}{\partial Y} & \frac{\partial v}{\partial Z} \end{bmatrix} = \begin{bmatrix} \frac{f_x}{Z} & 0 & -\frac{f_x X}{Z^2} \\ 0 & \frac{f_y}{Z} & -\frac{f_y Y}{Z^2} \end{bmatrix} \]
- \(\frac{\partial q}{\partial \delta \xi}\)为变换之后的点对位姿变换的导数,即SE3上的李代数求导:
\[ \begin{aligned} \frac{\partial q}{\partial \delta \xi} &= \begin{bmatrix} I & -q^\wedge \end{bmatrix}_{3\times6} \\ &= \begin{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 &1 \end{bmatrix} \begin{bmatrix} 0 & q[2] & -q[1] \\ -q[2] & 0 & q[0] \\ q[1] & -q[0] & 0 \end{bmatrix} \end{bmatrix} \\ &= \begin{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 &1 \end{bmatrix} \begin{bmatrix} 0 & Z & -Y \\ -Z & 0 & X \\ Y & -X & 0 \end{bmatrix} \end{bmatrix} \end{aligned} \]
一般情况下,可以把\(\frac{\partial u}{\partial q}\frac{\partial q}{\partial \delta \xi}\)合起来,得到
\[ \begin{aligned} \frac{\partial u}{\partial \delta \xi} = \begin{bmatrix} \frac{f_x}{Z} & 0 & -\frac{f_x X}{Z^2} & -\frac{f_x X Y}{Z^2} & f_x+\frac{f_x X^2}{Z^2} & -\frac{f_x Y}{Z} \\ 0 & \frac{f_y}{Z} & -\frac{f_y Y}{Z^2} & -f_y - \frac{f_y Y^2}{Z^2} & \frac{f_y X Y}{Z^2} & \frac{f_y X}{Z} \end{bmatrix} \end{aligned} \]
如果使用虚拟点进行计算(DSO),那么,第i帧相机坐标系点\(P_i\)转换到第j帧相机坐标系的点\(P_j\)可以如下表示:
\[ q=P_j=\frac{P_j^{virtual}}{d_{pi}} \]
\[ \Longrightarrow \left \{ \begin{aligned} X=P_j[0]=\frac{P_j^{virtual}[0]}{d_{pi}} \\ Y=P_j[1]=\frac{P_j^{virtual}[1]}{d_{pi}} \\ Z=P_j[2]=\frac{P_j^{virtual}[2]}{d_{pi}} \end{aligned} \right. \]
使用上式对\(\frac{\partial u}{\partial q}\frac{\partial q}{\partial \delta \xi}\)进行替换,得到:
\[ \begin{aligned} \frac{\partial u}{\partial \delta \xi} = \begin{bmatrix} \frac{f_x d_{pi}}{P_j^{virtual}[2]} & 0 & -\frac{f_x P_j^{virtual}[0] d_{pi} }{P_j^{virtual}[2]^2} & -\frac{f_x P_j^{virtual}[0] P_j^{virtual}[1]}{P_j^{virtual}[2]^2} & f_x+\frac{f_x P_j^{virtual}[0]^2}{P_j^{virtual}[2]^2} & -\frac{f_x P_j^{virtual}[1]}{P_j^{virtual}[2]} \\ 0 & \frac{f_y d_{pi}}{P_j^{virtual}[2]} & -\frac{f_y P_j^{virtual}[1] d_{pi}}{P_j^{virtual}[2]^2} &-f_y - \frac{f_y P_j^{virtual}[1]^2}{P_j^{virtual}[2]^2} & \frac{f_y P_j^{virtual}[0] P_j^{virtual}[1]}{P_j^{virtual}[2]^2} & \frac{f_y P_j^{virtual}[0]}{P_j^{virtual}[2]} \end{bmatrix} \end{aligned} \]
于是,最终得到误差e对位姿(李代数)的雅克比
\[ J^T=\frac{\partial I_1}{\partial u} \frac{\partial u}{\partial \delta \xi} \]
3.5.4. 对逆深度求导
与前文保持一致:
\[ P_j=R P_i + t= R\frac{P_i'}{d_{pi}}+t \]
\[ P_j^{virtual}= d_{pi} P_j = R P_i' + t d_{pi} \]
\[ \Longrightarrow P_j=\frac{P_j^{virtual}}{d_{pi}} \]
根据上面的$ q=P_j=$,残差对逆深度的导数如下:
\[ \begin{aligned} \frac{\partial e}{\partial \delta d_{pi}} = \frac{\partial I_1}{\partial u} \frac{\partial u}{\partial q} \frac{\partial q}{\partial d_{pi}} \end{aligned} \]
其中,\(P_j^{virtual} = R P_i' + t d_{pi}\)也是关于\(d_{pi}\)的函数,根据分数求导公式,可得\(\frac{\partial q}{\partial d_{pi}}\)
\[ \frac{\partial q}{\partial d_{pi}}=\frac{t d_{pi}-P_j^{virtual}}{d_{pi}^2} \]
其中,t为从第i帧相机坐标系到第j帧相机坐标系变换的平移量
在这里,残差对逆深度的导数为:
\[ \begin{aligned} \frac{\partial e}{\partial \delta d_{pi}} &= \frac{\partial I_1}{\partial u} \frac{\partial u}{\partial q} \frac{\partial q}{\partial d_{pi}} \\ &= \frac{\partial I_1}{\partial u} \begin{bmatrix} \frac{f_x}{Z} & 0 & -\frac{f_x X}{Z^2} \\ 0 & \frac{f_y}{Z} & -\frac{f_y Y}{Z^2} \end{bmatrix} (\frac{t d_{pi}-P_j^{virtual}}{d_{pi}^2}) \\ &= \frac{\partial I_1}{\partial u} \begin{bmatrix} \frac{f_x d_{pi}}{P_j^{virtual}[2]} & 0 & -\frac{f_x P_j^{virtual}[0] d_{pi}}{P_j^{virtual}[2]^2} \\ 0 & \frac{f_y d_{pi}}{P_j^{virtual}[2]} & -\frac{f_y P_j^{virtual}[1] d_{pi}}{P_j^{virtual}[2]^2} \end{bmatrix} (\frac{t d_{pi}-P_j^{virtual}}{d_{pi}^2}) \\ &= \frac{\partial I_1}{\partial u} \begin{bmatrix} f_x & 0 \\ 0 & f_y \end{bmatrix} \begin{bmatrix} \frac{1}{P_j^{virtual}[2]} & 0 & -\frac{ P_j^{virtual}[0] }{P_j^{virtual}[2]^2} \\ 0 & \frac{1}{P_j^{virtual}[2]} & -\frac{ P_j^{virtual}[1] }{P_j^{virtual}[2]^2} \end{bmatrix} (\frac{t d_{pi}-P_j^{virtual}}{d_{pi}}) \\ &= \begin{bmatrix} d_x & d_y \end{bmatrix} \begin{bmatrix} f_x & 0 \\ 0 & f_y \end{bmatrix} \frac{1}{P_j^{virtual}[2]} \begin{bmatrix} 1 & 0 & -\frac{ P_j^{virtual}[0] }{P_j^{virtual}[2]} \\ 0 & 1 & -\frac{ P_j^{virtual}[1] }{P_j^{virtual}[2]} \end{bmatrix} (t - q) \end{aligned} \]
到这里,是时候讨论\(P_j^{virtual}\)的内在意义了:
根据虚拟点\(P_j^{virtual}\)的定义
\[ P_j^{virtual}= d_{pi} P_j = R P_i' + t d_{pi} \]
对虚拟点\(P_j^{virtual}\)也转换到归一化平面上
\[ \begin{aligned} P_j^{virtual-normal}= \begin{bmatrix} \frac{P_j^{virtual}[0]}{P_j^{virtual}[2]} \\ \frac{P_j^{virtual}[1]}{P_j^{virtual}[2]} \\ 1 \end{bmatrix} \begin{bmatrix} \frac{d_{pi} P_j[0]}{d_{pi} P_j[2]} \\ \frac{d_{pi} P_j[1]}{d_{pi} P_j[2]} \\ 1 \end{bmatrix}= \begin{bmatrix} \frac{P_j[0]}{P_j[2]} \\ \frac{P_j[1]}{P_j[2]} \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{q[0]}{q[2]} \\ \frac{q[1]}{q[2]} \\ 1 \end{bmatrix} \end{aligned} \]
因此,最终可以将上面的残差对逆深度的导数进一步化简:
\[ \begin{aligned} \frac{\partial e}{\partial \delta d_{pi}} &= \begin{bmatrix} d_x & d_y \end{bmatrix} \begin{bmatrix} f_x & 0 \\ 0 & f_y \end{bmatrix} \frac{1}{P_j^{virtual}[2]} \begin{bmatrix} 1 & 0 & -\frac{ P_j^{virtual}[0] }{P_j^{virtual}[2]} \\ 0 & 1 & -\frac{ P_j^{virtual}[1] }{P_j^{virtual}[2]} \end{bmatrix} (t - q) \\ &= \begin{bmatrix} d_x f_x & d_y f_y \end{bmatrix} \frac{1}{P_j^{virtual}[2]} \begin{bmatrix} 1 & 0 & -\frac{ q[0] }{q[2]} \\ 0 & 1 & -\frac{ q[1] }{q[2]} \end{bmatrix} \begin{bmatrix} t[0]-q[0] \\ t[1]-q[1] \\ t[2]-q[2] \end{bmatrix} \\ &= \begin{bmatrix} d_x f_x & d_y f_y \end{bmatrix} \frac{1}{P_j^{virtual}[2]} \begin{bmatrix} 1 & 0 & -\frac{ q[0] }{q[2]} \\ 0 & 1 & -\frac{ q[1] }{q[2]} \end{bmatrix} \begin{bmatrix} t[0] \\ t[1] \\t[2] \end{bmatrix} \\ &= \begin{bmatrix} d_x f_x & d_y f_y \end{bmatrix} \frac{1}{P_j^{virtual}[2]} \begin{bmatrix} 1 & 0 & -\frac{ P_j^{virtual}[0] }{P_j^{virtual}[2]} \\ 0 & 1 & -\frac{ P_j^{virtual}[1] }{P_j^{virtual}[2]} \end{bmatrix} \begin{bmatrix} t[0] \\ t[1] \\t[2] \end{bmatrix} \end{aligned} \]
总结PPT:

DSO作者采用(齐次点)\(P_j^{virtual}\)的目的是希望可以简化的雅克比求导过程。
4. 初始化

- 将图像分成许多个32x32的block
- 在block内创建直方图hist0
- 直方图,统计block内像素点的梯度
- 取block内直方图的梯度中位数作为阈值
- 使用 size=3x3 的窗口, 对每个block的阈值进行滤波
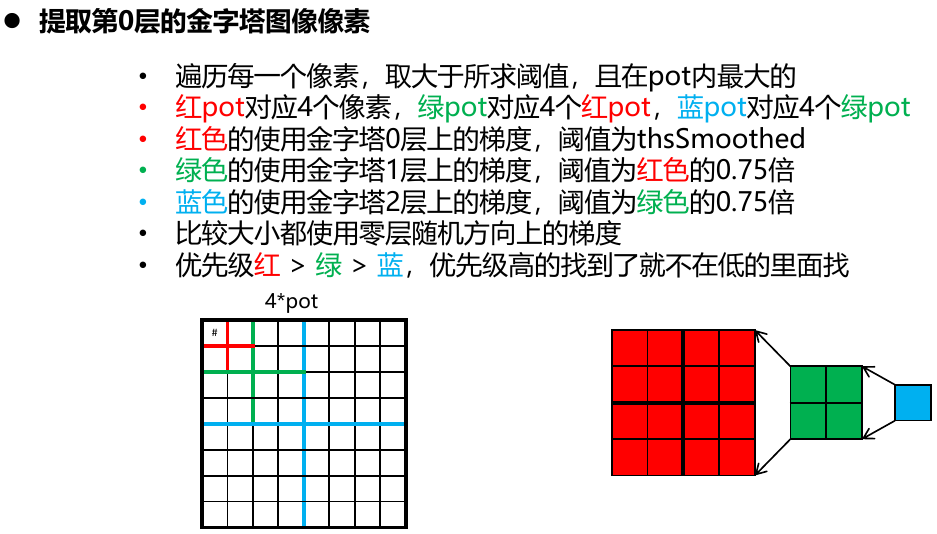
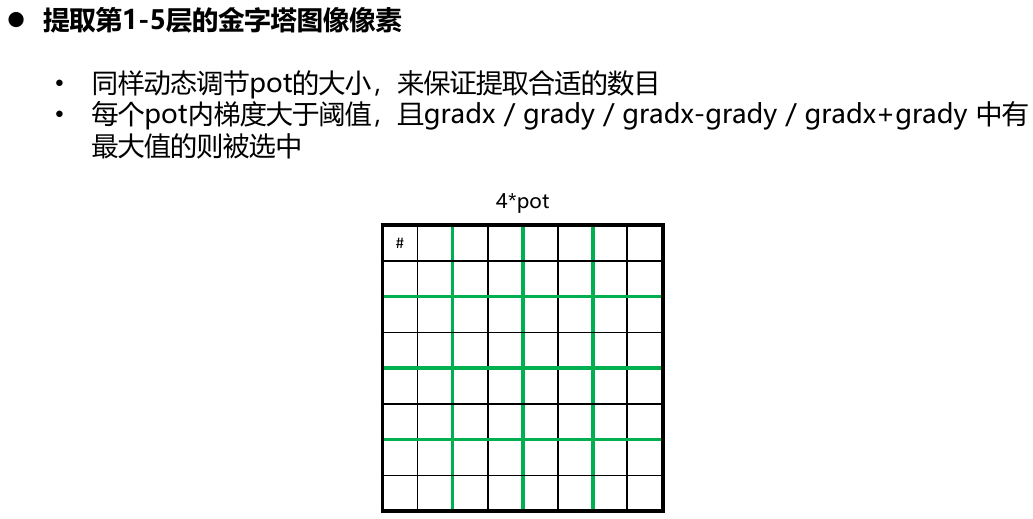
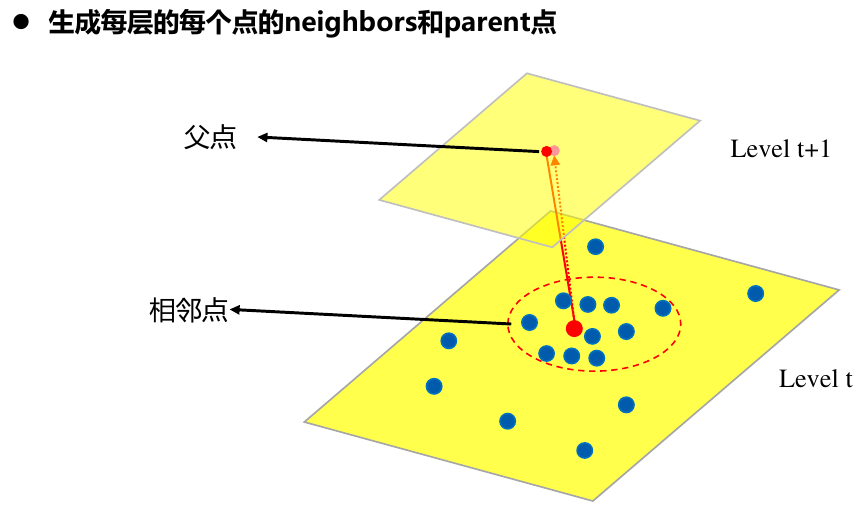
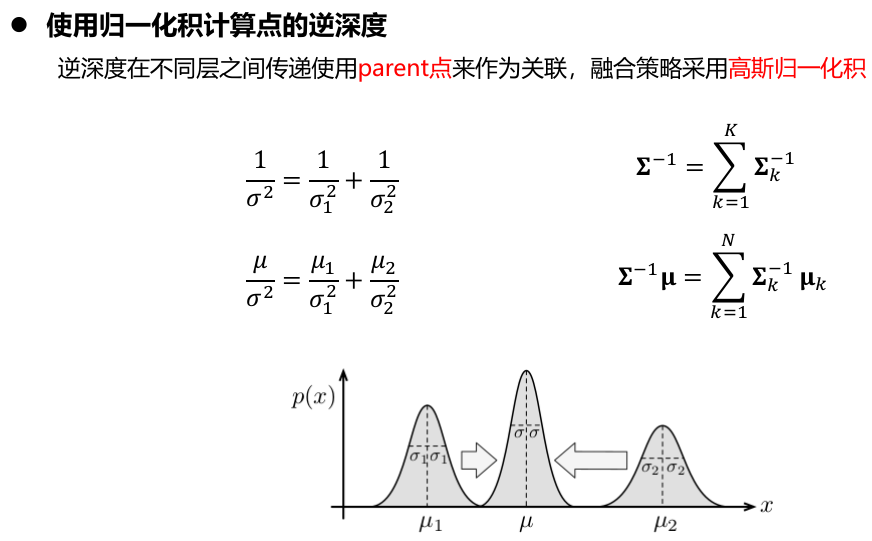
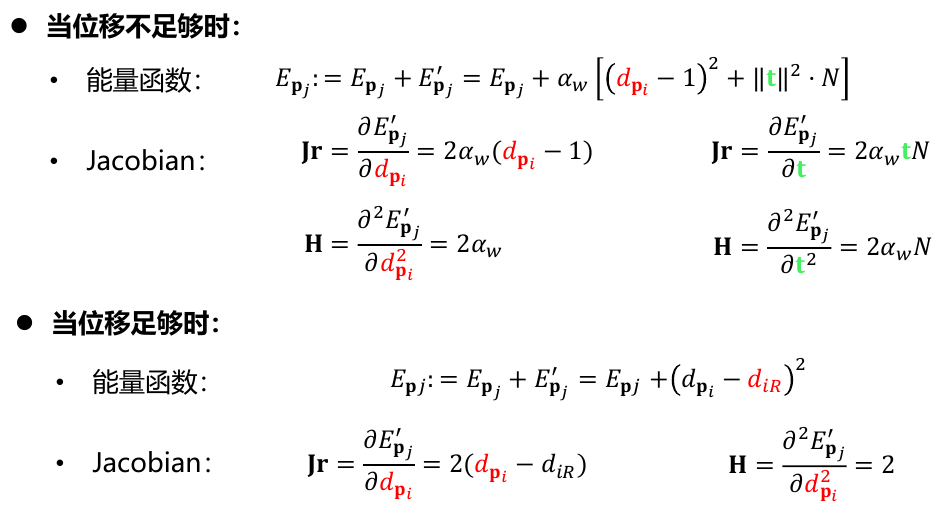
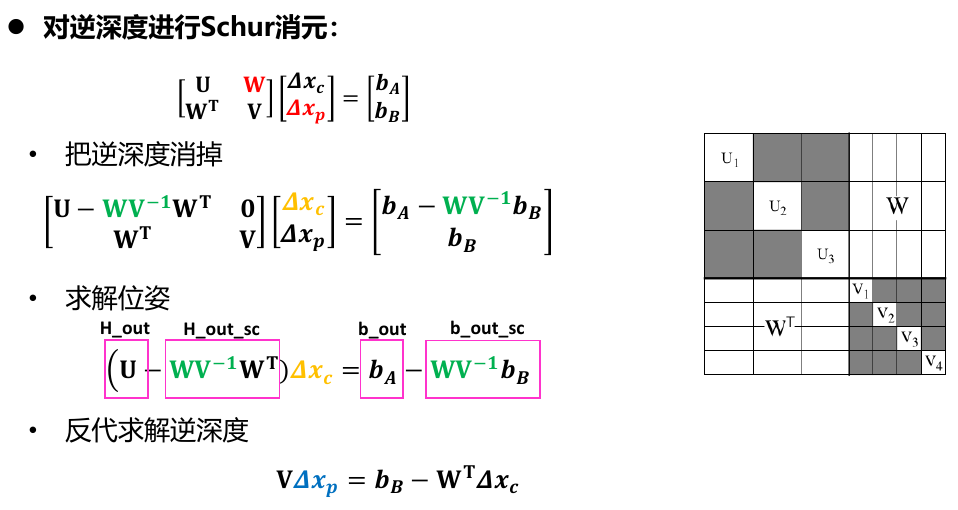
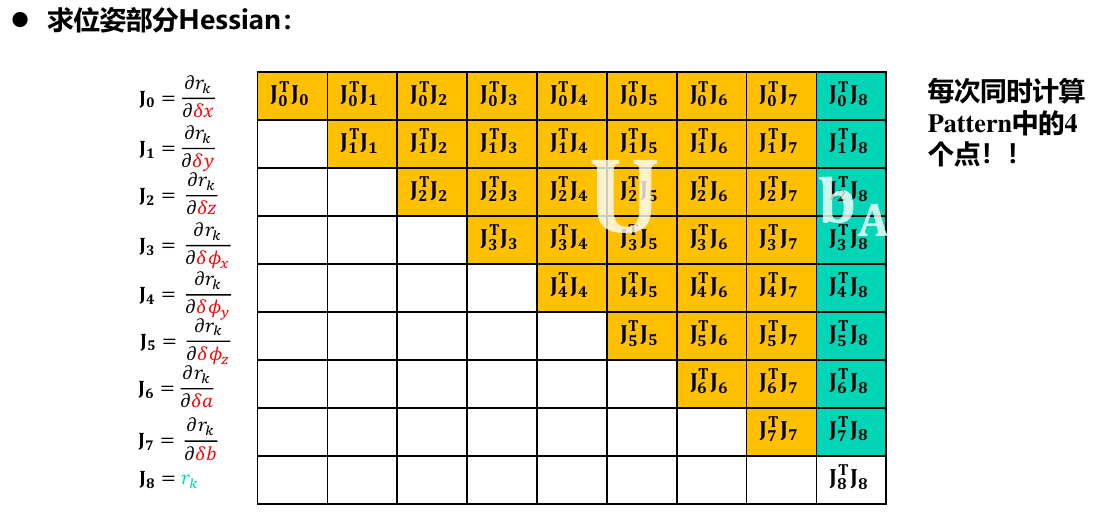
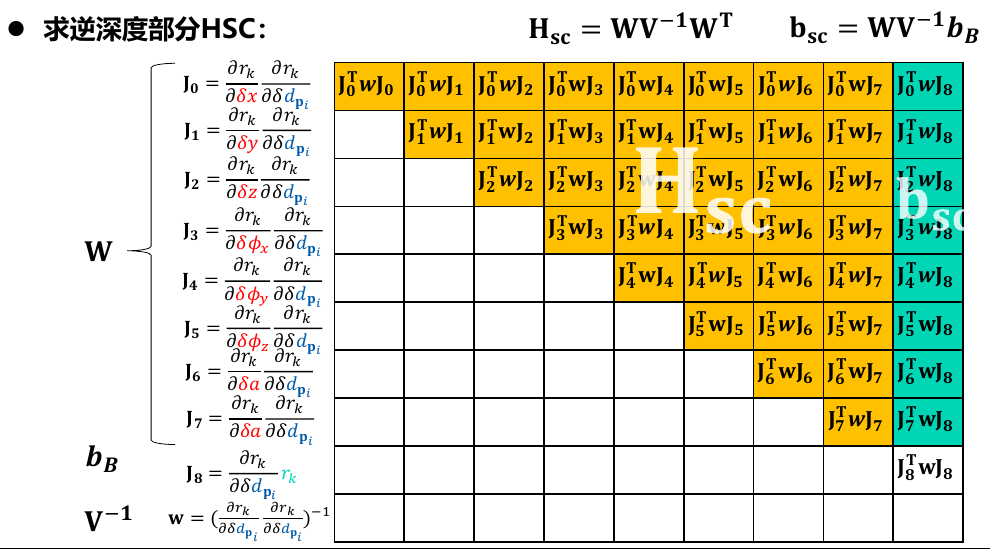
DSO代码中初始化时候的雅克比:
\[ \begin{aligned} J &= \begin{bmatrix} \frac{\partial e}{\partial \delta x} & \frac{\partial e}{\partial \delta y} & \frac{\partial e}{\partial \delta z} & \frac{\partial e}{\partial \delta \phi_x} & \frac{\partial e}{\partial \delta \phi_y} & \frac{\partial e}{\partial \delta \phi_z} & \frac{\partial e}{\partial a} & \frac{\partial e}{\partial b} & \frac{\partial e}{\partial d_{pi_1}} & 0 & \cdots & 0 \\ \frac{\partial e}{\partial \delta x} & \frac{\partial e}{\partial \delta y} & \frac{\partial e}{\partial \delta z} & \frac{\partial e}{\partial \delta \phi_x} & \frac{\partial e}{\partial \delta \phi_y} & \frac{\partial e}{\partial \delta \phi_z} & \frac{\partial e}{\partial a} & \frac{\partial e}{\partial b} & 0 & \frac{\partial e}{\partial d_{pi_2}} & \cdots & 0 \\ \frac{\partial e}{\partial \delta x} & \frac{\partial e}{\partial \delta y} & \frac{\partial e}{\partial \delta z} & \frac{\partial e}{\partial \delta \phi_x} & \frac{\partial e}{\partial \delta \phi_y} & \frac{\partial e}{\partial \delta \phi_z} & \frac{\partial e}{\partial a} & \frac{\partial e}{\partial b} & 0 & 0 & \ddots & 0 \\ \frac{\partial e}{\partial \delta x} & \frac{\partial e}{\partial \delta y} & \frac{\partial e}{\partial \delta z} & \frac{\partial e}{\partial \delta \phi_x} & \frac{\partial e}{\partial \delta \phi_y} & \frac{\partial e}{\partial \delta \phi_z} & \frac{\partial e}{\partial a} & \frac{\partial e}{\partial b} & 0 & 0 & \cdots & \frac{\partial e}{\partial d_{pi_n}} \end{bmatrix} \\ &= \begin{bmatrix} \begin{bmatrix} & & & & & & & J_{c} & & & & & & & & & & \end{bmatrix} & \frac{\partial e}{\partial d_{pi_1}} & 0 & \cdots & 0 \\ \begin{bmatrix} & & & & & & & J_{c} & & & & & & & & & & \end{bmatrix} & 0 & \frac{\partial e}{\partial d_{pi_2}} & \cdots & 0 \\ \begin{bmatrix} & & & & & & & J_{c} & & & & & & & & & & \end{bmatrix} & 0 & 0 & \ddots & 0 \\ \begin{bmatrix} & & & & & & & J_{c} & & & & & & & & & & \end{bmatrix} & 0 & 0 & \cdots & \frac{\partial e}{\partial d_{pi_n}} \end{bmatrix} \end{aligned} \]
其中,前6个是残差对位姿(SE3)的偏导,继续后两个是残差对光度参数(a,b)的偏导,然后就是残差对该层图像各个点的逆深度的偏导。
那么对应的hessian近似可以写成这个样子:
\[ \begin{aligned} J^T J &= \begin{bmatrix} \begin{bmatrix} & & & & \\ & & & & \\ & & n*J_c^TJ_c & \\ & & & & \\ & & & & \\ \end{bmatrix} , & \begin{bmatrix} \\ \\ J_c^T \\ \\ \\ \end{bmatrix} \frac{\partial e}{\partial d_{pi_1}} ,& \begin{bmatrix} \\ \\ J_c^T \\ \\ \\ \end{bmatrix} \frac{\partial e}{\partial d_{pi_2}} ,& \cdots & \begin{bmatrix} \\ \\ J_c^T \\ \\ \\ \end{bmatrix} \frac{\partial e}{\partial d_{pi_n}} \\ \frac{\partial e}{\partial d_{pi_1}} \begin{bmatrix} & & & J_c & & & \end{bmatrix} & \frac{\partial e}{\partial d_{pi_1}} \cdot \frac{\partial e}{\partial d_{pi_1}} & 0 & \cdots & 0 \\ \frac{\partial e}{\partial d_{pi_2}} \begin{bmatrix} & & & J_c & & & \end{bmatrix} & 0 & \frac{\partial e}{\partial d_{pi_2}} \cdot \frac{\partial e}{\partial d_{pi_2}} & \cdots & 0 \\ \vdots & 0 & 0 & \ddots & 0 \\ \frac{\partial e}{\partial d_{pi_n}} \begin{bmatrix} & & & J_c & & & \end{bmatrix} & 0 & 0 & \cdots & \frac{\partial e}{\partial d_{pi_n}} \cdot \frac{\partial e}{\partial d_{pi_n}} \end{bmatrix} \\ &= \begin{bmatrix} \begin{bmatrix} \\ & & U(or B) & \\ \\ \end{bmatrix} , & \begin{bmatrix} \\ & & & & W(or E) & & & & \\ \\ \end{bmatrix} \\ \\ \begin{bmatrix} \\ \\ \\ & W^T (or E^T) & \\ \\ \\ \\ \end{bmatrix} ,& \begin{bmatrix} & \\ & \\ & \\ &&&& V (or C) &&&& \\ & \\ & \\ & \\ \end{bmatrix} \end{bmatrix} \end{aligned} \]
Tips
在应用舒尔补的时候,需要计算\(WV^{-1}W^T\),那么有:
\[ \begin{aligned} WV^{-1}W^T &=V^{-1}WW^T \\ &=(V^{-1}[1][1]W.col[1]W^T.row[1]+V^{-1}[2][2]W.col[2]W^T.row[2]+ \\ &\cdots+V^{-1}[n][n]W.col[n]W^T.row[n]) \end{aligned} \]
其中,
- \(W.col[]\)表示\(J^TJ\)矩阵右上角块的按列取
- \(W^T.row[]\)表示\(J^TJ\)矩阵左下角块的按行取
- 优点:这样就可以把大矩阵的运算变成小矩阵的加法运算,通过遍历观测到的每一个点,计算一个8x8的小矩阵,对这些矩阵进行求和,就可以得到原本需要计算(8xn)x(nx8)大矩阵来得到的\(WV^{-1}W^T\)。 (DSO就是通过这样的思路+SSE进行加速运算)
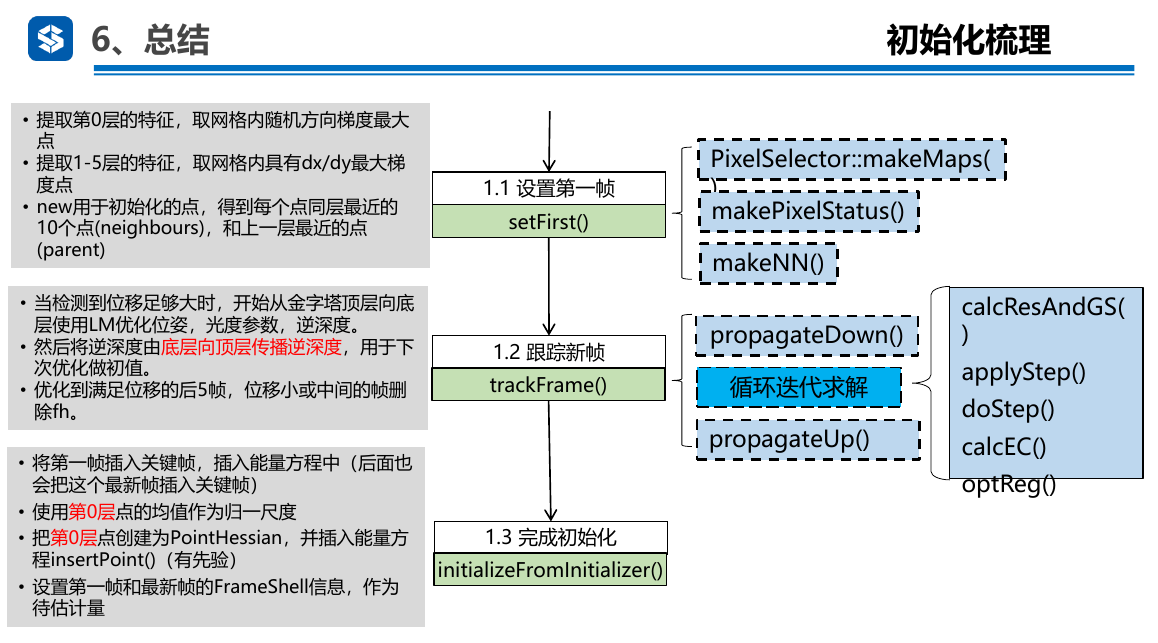
4.1. 初始化流程总结
5. DSO框架