1. [附录]-几种积分方法
2. 龙格库塔数值积分法
我们的目的是对如下形式的非线性微分方程在给定一个时间间隔\(\Delta t\)进行积分,
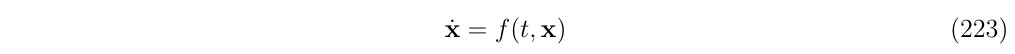
从而将微分方程转化为差分方程
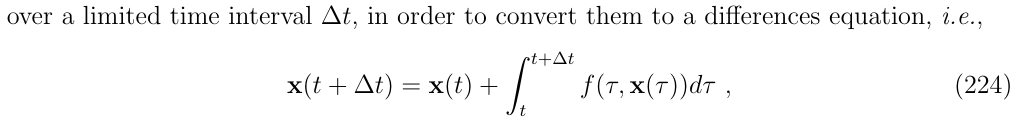
或者是这种形式(假设\(t_n=n\Delta t\)和\(x_n \triangleq x(t_n)\))
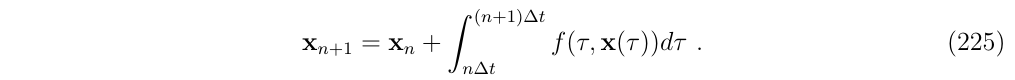
龙格-库塔(RK)方法是最常用的方法之一,这些方法使用几个迭代来估计区间上的导数,然后利用这个导数在时间步\(\Delta t\)上进行积分。
在接下来的小节中,将介绍几种RK方法,从最简单的方法到最通用的方法,并根据它们最常用的名称进行命名。
2.1. 欧拉方法(The Euler method)
欧拉方法假设导数\(f(\cdot)\)是常数,因此有:
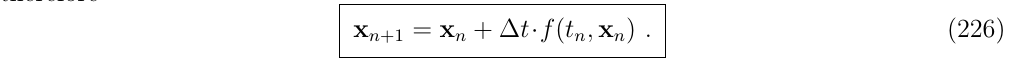
作为一般的RK方法,这对应于一个单阶段方法,它可以描述如下:
- 计算在初始点处的导数
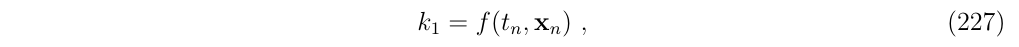
- 使用它来计算积分,到结束点
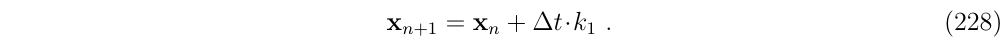
2.2. 中点法(The midpoint method)
中点法假设导数是区间中点处的导数,然后进行一次迭代来计算x在这个中点的值,如
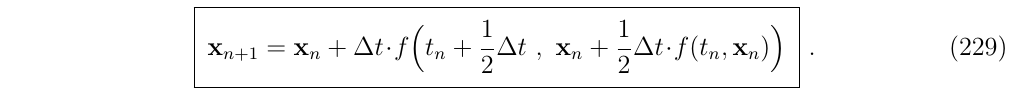
中点法可以解释为以下两步法
- 使用欧拉方法积分,直到中点 (使用前面定义的k1)
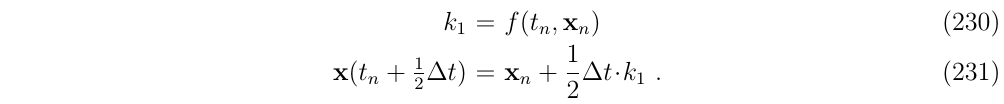
- 然后使用这个值来计算中间点k2的导数,然后对后半段进行积分
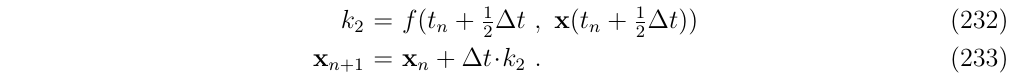
2.3. 4阶龙格库塔法(The RK4 method)
这通常被简单地称为龙格-库塔方法,它用四个阶段或迭代来计算积分,有四个导数,\(k1 \cdots k4\),是按顺序得到的。然后将这些导数(或斜率)加权平均,得到区间内导数的4阶估计值。
RK4方法比上面两种方法的更好,其积分计算步骤是:
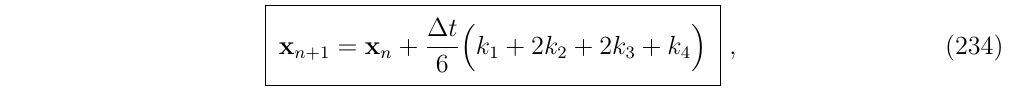
也就是说,增量是通过假设一个斜率来计算的这个斜率是k1 k2 k3 k4的加权平均值,其中k1 k2 k3 k4按下面计算:
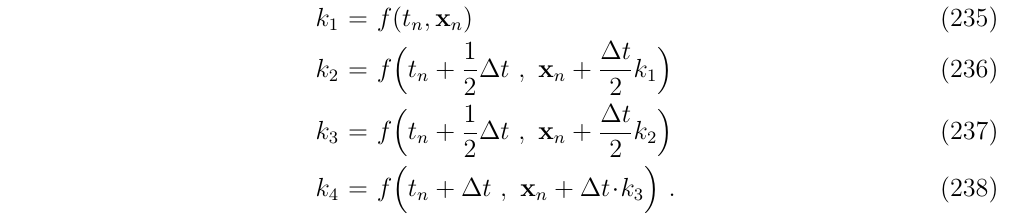
不同的斜率有如下的解释:
- k1是区间开始时的斜率,使用\(x_n\)来计算. (欧拉方法)
- k2是区间中点处的斜率,使用\(x_n+\frac{1}{2}\Delta t k_1\)来计算。(中点法)
- k3还是中点的斜率,不过使用\(x_n+\frac{1}{2}\Delta t k_2\)计算
- k4是区间最后的斜率,使用\(x_n+\Delta t k_3\)计算
2.4. 通用龙格库塔法(General Runge-Kutta method)
更详细的RK方法是可能的,它们的目标是减少误差和/或增加稳定性,它们具有通用的形式为:
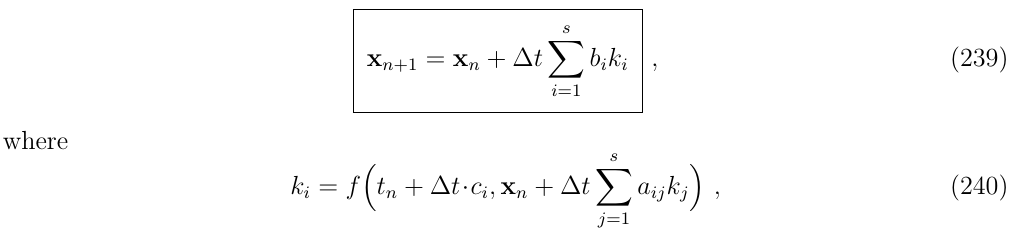
也就是说,迭代的次数(方法的顺序)是s,平均权值由bi定义,评价时间瞬间由ci定义,斜率ki是用aij值确定的,根据aij的结构,可以使用显式或隐式RK方法。

3. 闭式积分方法(Closed-form integration methods)
在许多情况下,可以得到一个封闭形式的积分步骤表达式,我们现在考虑一阶线性微分方程的情况
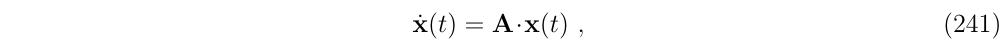
也就是说,这个关系是线性的,在区间内是常数,在这种情况下,积分区间[tn, tn + t],可以得到:
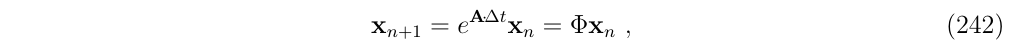
其中,\(\Phi\)就是常说的状态转移矩阵,这个状态转移矩阵的泰勒展开如下:
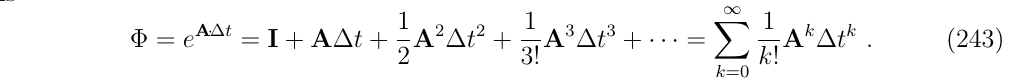
当写出这串由已知常数矩阵A构成的序列时,有时有可能可以写成闭式的解,一些例子如下
3.1. 角度误差的积分
例如,考虑无偏差和噪声的角度误差(纯净版的式133)
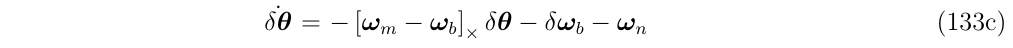
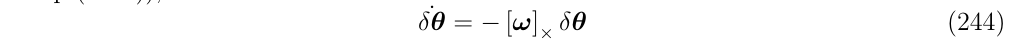
它的转移矩阵可以写成泰勒级数
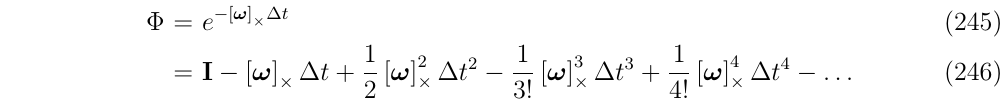
现在,定义\(\boldsymbol{w}\Delta t \triangleq \boldsymbol{u} \Delta \theta\),旋转轴和旋转的角度,然后应用式53,可以得到
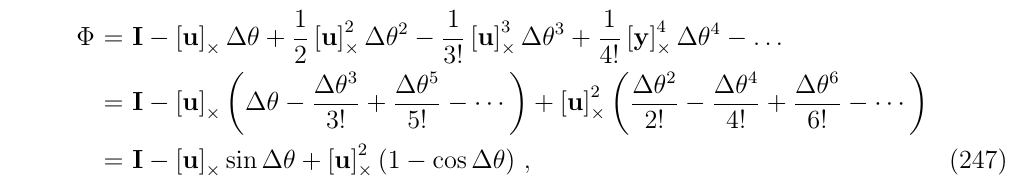
这个解对应于一个旋转矩阵,(根据式51,可以进一步化为转置),即
\[ \Phi=R\{-\boldsymbol{u} \Delta \theta \}=R\{-\boldsymbol{w} \Delta t\}=R\{\boldsymbol{w} \Delta t\}^T \]
根据罗德里格斯公式,可以得到闭式解:
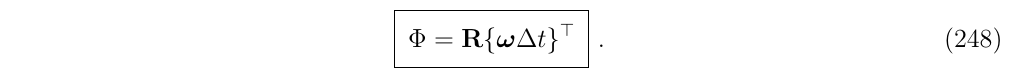
3.2. 简化版IMU例子
考虑简化版的IMU系统,其误差状态方程为:
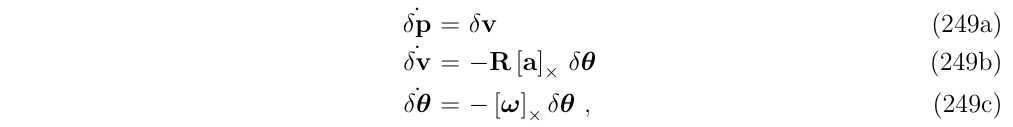
其中,\((a,w)\)是已经去除了重力和传感器的偏差的IMU的测量,这个系统的状态向量和矩阵如下:
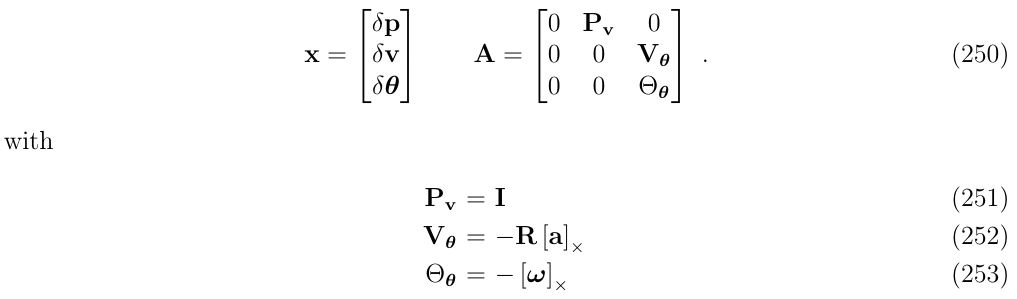
其在一个时间步\(\Delta t\)的积分为\(\boldsymbol{x}_{n+1}=e^{\boldsymbol{A}\Delta t}\cdot \boldsymbol{x}_n\)。
状态转移矩阵\(\Phi=e^{\boldsymbol{A\Delta t}}\),泰勒展开如下:
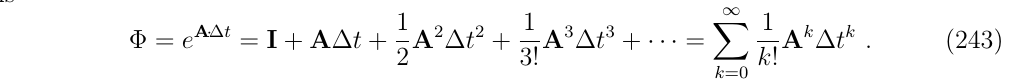
我们可以写出矩阵A的几次幂来说明它们的一般形式
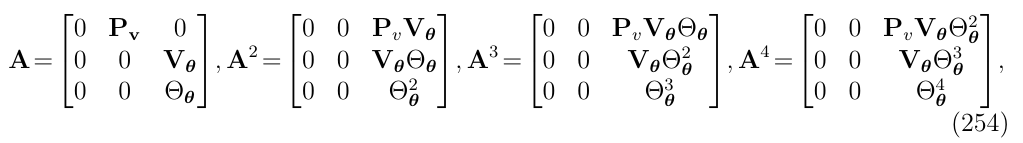
从这里可以看出,对于k>1,有如下一般形式:
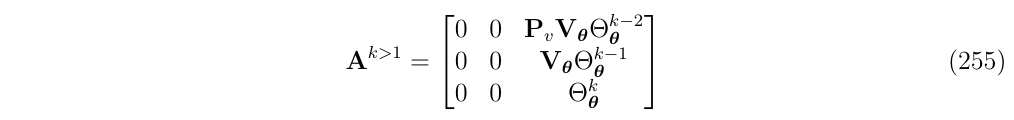
我们可以观察这些A的次方项,有固定的部分以及会增长的次方项\(\Theta_\Theta\)
下面,对状态转移矩阵\(\Phi\)进行分块讨论:
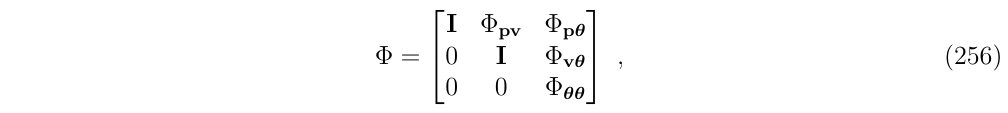
让我们一步一步推进,探索矩阵\(\Phi\)的所有非零块
- Trivial diagonal terms (对角线前2个)
没什么好说,就是单位阵I
- Rotational diagonal term (对角线第3项)
接下来是对角的旋转项\(\Phi_{\theta \theta}\),将新的角误差与旧的角误差联系起来,写出这一项的泰勒级数
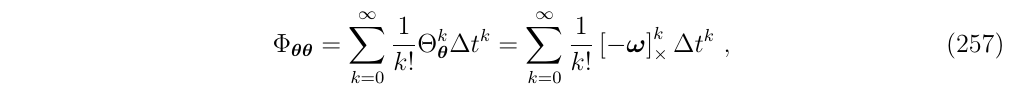
正如我们在前一节中看到的,它对应于我们熟知的旋转矩阵
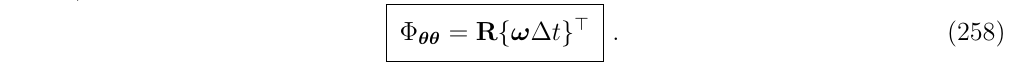
- Position-vs-velocity term (第一行第二列)
这是最简单的非对角项
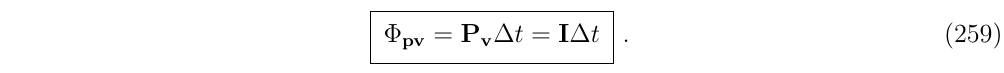
- Velocity-vs-angle term (第二行第三列)
根据上面的推导,写出状态转移矩阵\(\Phi\)的第二行第三列\(\Phi_{v,\theta}\)的叠加形式:
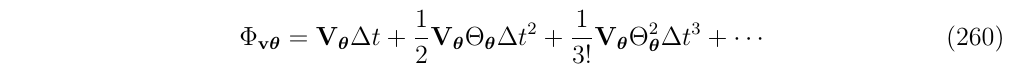
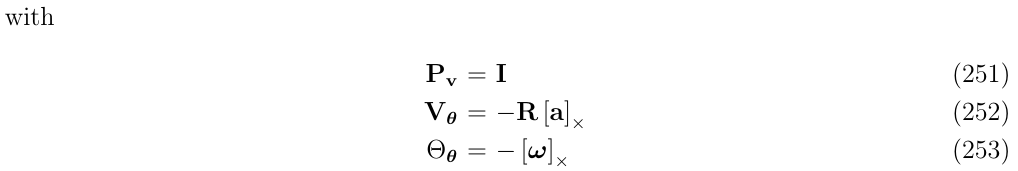
在这里,有两种选择:
(1)我们可以把级数的第一个有效项截断,即只保留\(\Phi_{v,\theta}=V_{\theta}\Delta t\) ,但是这样就不是闭式解了。(有关使用这种简化方法的结果,请参见下一节)
(2)第二种方法,把因式\(V_{\theta}\)提取出来,如下
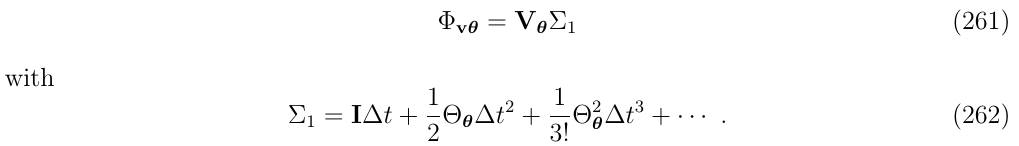
可以看到,\(\Sigma_1\)项与我们之前写的\(\Phi_{\theta \theta}\)很像,但是有两处例外:
- \(\Sigma_1\)中的\(\Theta_\theta\)次方项与系数\(\frac{1}{k!}\)以及\(\Delta t\)次方项都不匹配。实际上,我们在这里\(\Sigma_1\)的标记
1表明\(\Theta_\theta\)次方项少了1次 - 还有一个问题是,在这个多项式的开头,少了一些内容。实际上,在这里\(\Sigma_1\)的标记
1表明少了1些项
关于第一个问题,可以采用式53的办法来解决,(会产生一个单位阵)
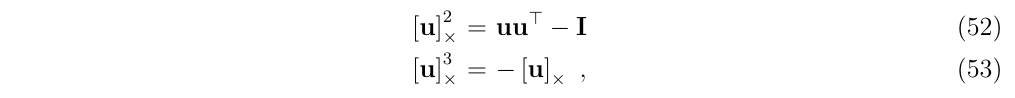
式53中的\(u\)是单位向量
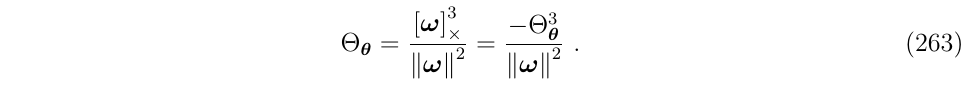
这个表达式允许我们增加\(\Theta_\theta\)指数,然后可重写式262如下:
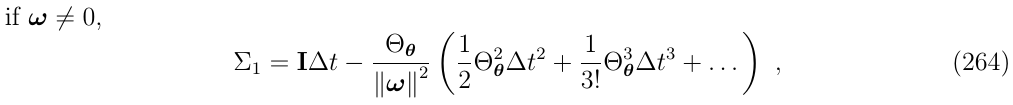
现在,次方项和其他系数都匹配了,但是整个式子还少了一些项,也就是第二个问题。第二个问题可以通过添加和减去缺少的项来解决,用它的封闭形式代替整个级数,即:
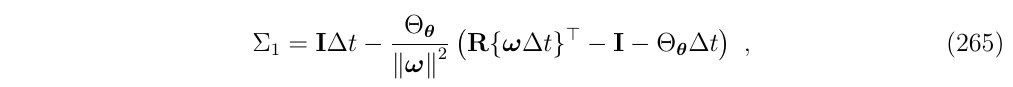
于是,最终,可以得到整一个比式解的形式:
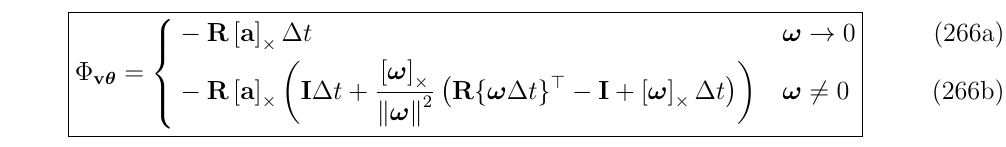
- Position-vs-angle term (第一行第三列)
对\(\Phi\)矩阵的第一行第三列\(\Phi_{p\theta}\)展开:
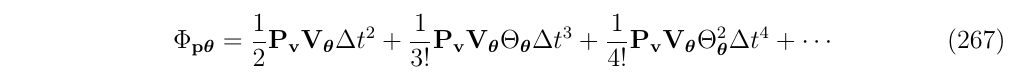
提取常数项公因式,写成如下形式:
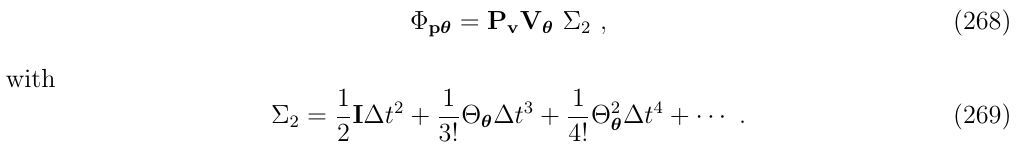
其中,我们标记下标2在\(\Sigma_2\)中:
- 对于上面多项式的每一项,都少了\(\Theta_\theta\)的2次
- 对于上面的多项式,缺少了开头两项
同样的处理,使用式263所用的方法,可以得到:
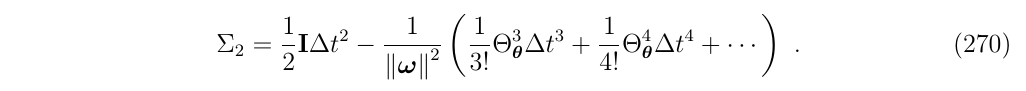
进一步地:
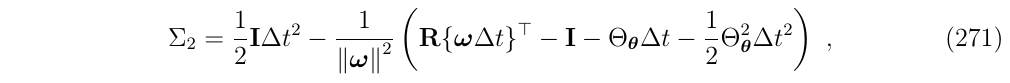
最终得到:
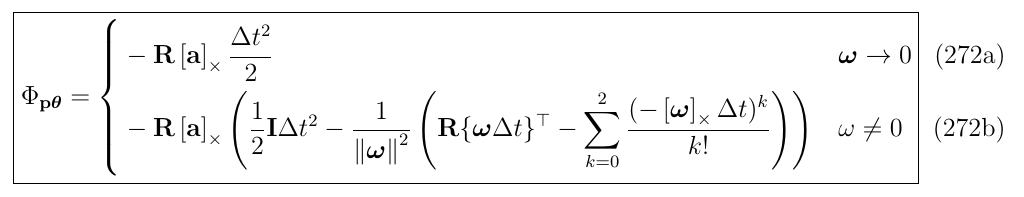
以上,就实现了简化版的IMU误差状态的状态转移矩阵\(\Phi\)的推导.
3.3. 完整版IMU例子
为了进一步对上述“简化版IMU”进行推广,我们需要更仔细地研究完整的IMU案例。
考虑一个完整的IMU系统,(式133)所示,可以表示成:
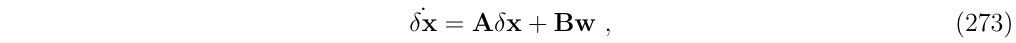
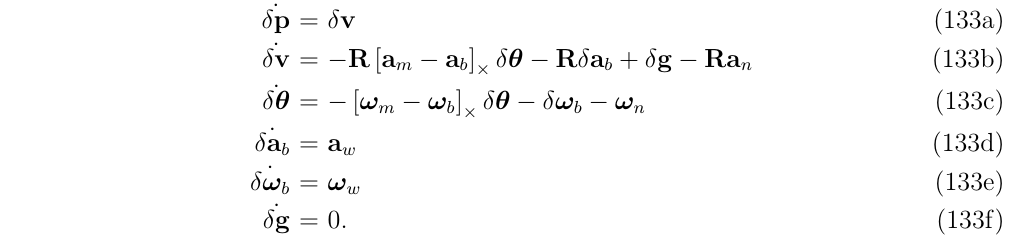
其中,动态矩阵A是块稀疏的,它的各个子块可以由(式133)确定:
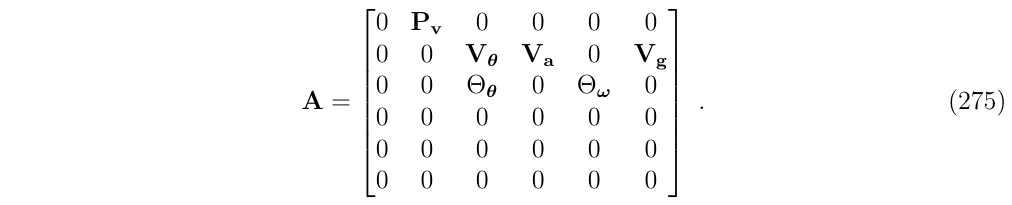
其中,
- \(P_v=I\)
- \(V_\theta=-R[a_m-a_b]_\times\)
- \(V_a=-R\)
- \(V_g=I\)
- \(\Theta_{\theta}=-[w_m-w_b]_\times\)
- \(\Theta_w=-I\)
同样的,写出矩阵A的次幂:

可以观察到:
- A的对角线上的唯一一项,旋转项\(\Theta_\theta\),在\(A^k\)的次方序列中向右和向上传播。所有不受传播影响的项都将消失,这个传播在以下3个方面影响了\(\{A^k \}\)序列的结构:
- 三次幂后,A的稀疏性趋于稳定,也就是说,对于大于3的幂,不再出现或消失非零块。
- 左上角3x3的子块,与前面例子中的简化IMU模型相对应,在这个例子里面仍然没有改变,因此,这个子块的闭式解就是前面得到的结果。
- 与角速度偏置(gyrometer bias)误差的相关项(在第5列中的项),产生了与\(\Theta_\theta\)次方序列相似的项,可以采用上面“简化版IMU”所使用的技巧进行求解。
我们对寻找构造闭式子块的状态转移矩阵\(\Phi\)的通用方法感兴趣,这与我们在“简化版IMU”所提到的\(\Sigma_1,\Sigma_2\)有关:
- 下标表示了序列中每个元素缺失的\(\Theta_\theta\)的次方数
- 下标表示了序列开头的项的数目
考虑到这个定义,现在定义一个序列\(\Sigma_n(X,y)\):
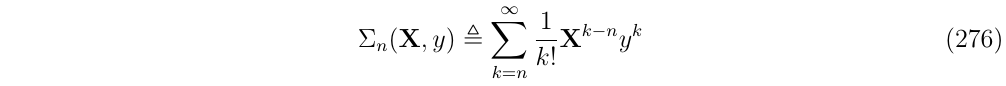
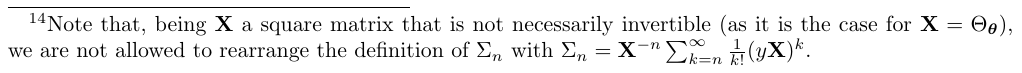
这个序列从第n项开始,并且每个元素都缺少了\(\Theta_\theta\)的n次方,即类似与\(\Sigma_1,\Sigma_2\):
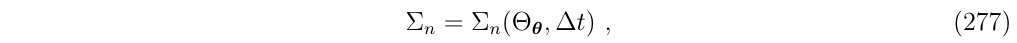
特别的,当n=0时,有\(\Sigma_0=R\{w\Delta t\}^T\)
现在,我们可以使用这个定义来写出状态转移矩阵\(\Phi\):
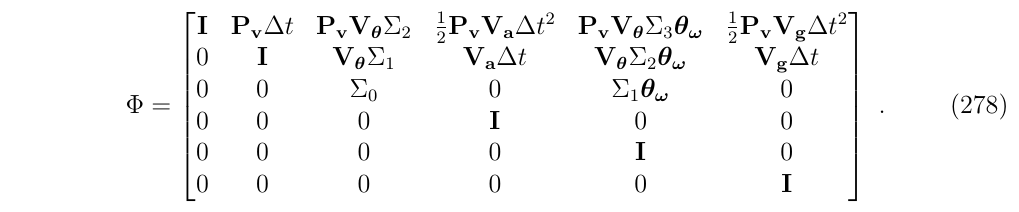
现在,我们的问题已经变成了寻找一个关于\(\Sigma_n\)的通用的,闭式的表达,下面再来看一眼之前推导出来的\(\Sigma\)
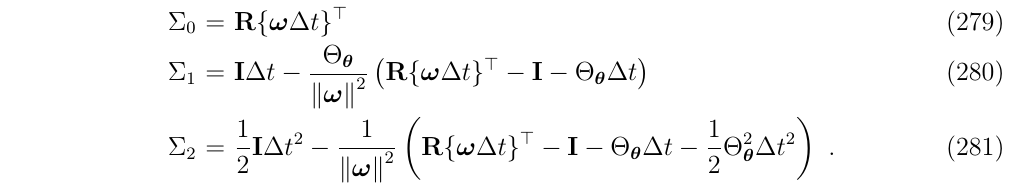
为了在\(\Sigma_3\)上得到推广,我们需要应用(式263)两次,因为一次只增加\(\Theta_\theta\)的2次幂,于是得到:
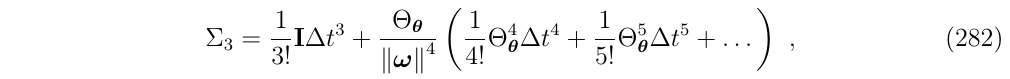
写成闭式解形式:
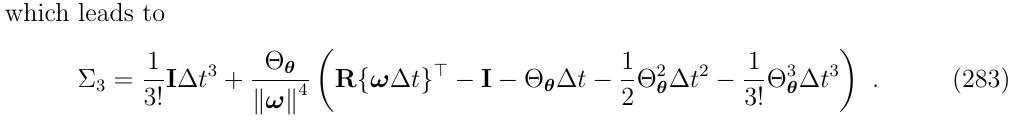
通过对上面\(\Sigma_0,\Sigma_1,\Sigma_2,\Sigma_3\)的观察,可以推导出关于\(\Sigma_n\)的闭式表达:
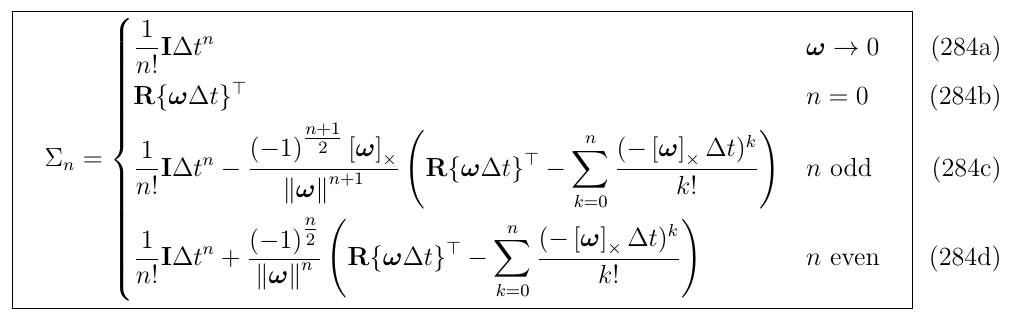
状态转移矩阵\(\Phi\)最后的闭式结果使用这个\(\Sigma_n\)来进行表达,即填充到(式278)。
可能需要注意的是,序列拥有了具有有限项的\(\Sigma_n\)表达,因此可以被高效的计算。也就是说,只要\(n < \infty\),那么\(\Sigma_n\)就可以有闭式表达,这是很常见的情况(\(n < \infty\))。对于当前这个例子来说,\(n \leq 3\)(式278)
4. 使用截断序列的近似方法(重点)
在前面的内容中,我们推导了复杂的状态转移矩阵\(\Phi\)的闭式表达,IMU驱动系统可以写成线性化的形式,即状态误差方程\(\dot{\delta x}=A\delta x\)
封闭形式的表达式可能总是令人感兴趣的,但是在什么程度上我们应该担心高阶误差及其对实际算法性能的影响还不清楚,这特别适用于IMU积分误差以相对较高的速率被观察到(并因此需要补偿)的系统,例如视觉-惯性或GPS-惯性融合方案
在这一部分,我们推导关于状态转移矩阵的近似,从相同的假设开始,状态转移矩阵被表达为泰勒展开序列,然后只对影响较大的项进行截断,截断可以使用system-wise和block-wise的方法。
4.1. system-wise截断
4.1.1. 一阶截断: 有限差分法
一种适用于以下系统的典型的、广泛的积分方法:
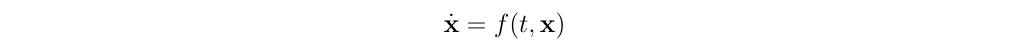
是基于有限差分法来计算导数的:
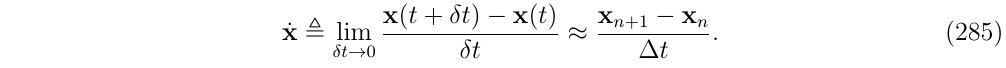
这产生:
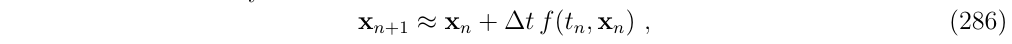
这与欧拉方法的精度相当,对函数f()在积分的起点处进行线性化,然后得到:
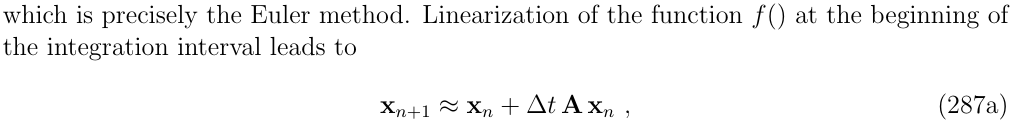
其中,\(A \triangleq \frac{\partial f}{\partial x}(t_n,x_n)\)是雅克比矩阵。这与线性化微分方程的指数解是完全等价的,然后在线性化的项进行截断,从而得到近似:
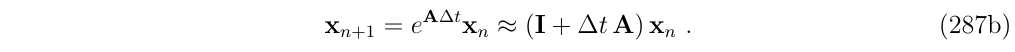
这说明了,上面提到的欧拉方法,是有限差分方法,是泰勒展开的一阶system-wise截断,也就是说,得到了如下的状态转移矩阵近似:
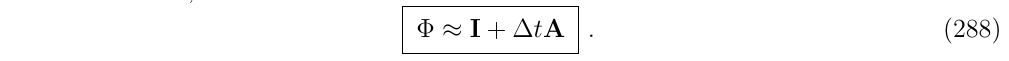
对于前面所提到的"简化版IMU"系统,对其状态转移矩阵应用一阶system-wise截断,得到近似矩阵:
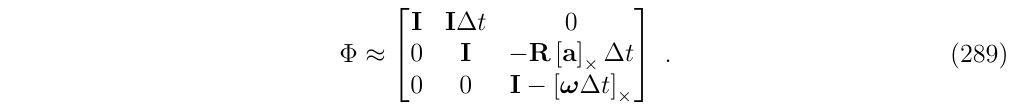
然而,在角度误差的积分一节中,我们已经讨论过了旋转项有一个紧凑的、封闭的表达,即\(\Phi_{\theta \theta}=R\cdot (w \Delta t)^T\),对上面的一阶system-wise截断的旋转项进行替换,最终得到:
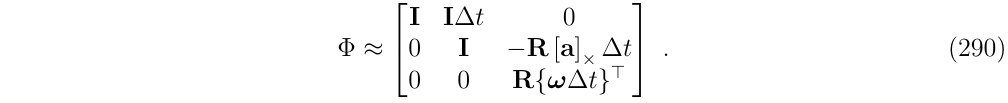
4.1.2. N阶截断
高阶截断将提高近似状态转移矩阵的精度,截断的一个特别有趣的顺序是最大限度地利用结果的稀疏性,换句话说,没有新的非零项出现的顺序。
对于简化版IMU的例子
回顾一下其系统矩阵A的次幂:
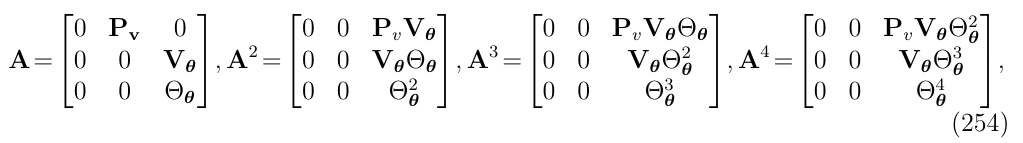
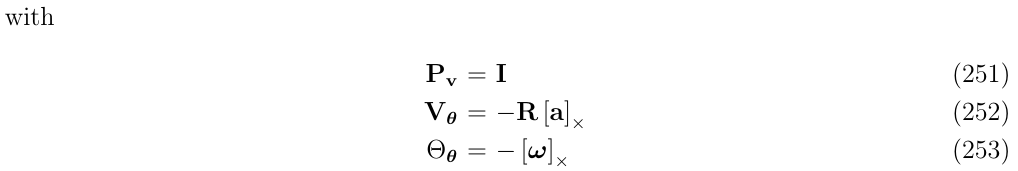
可以发现,在2阶之后,就没有非零项消失和产生,因此,取2阶进行截断,得到:
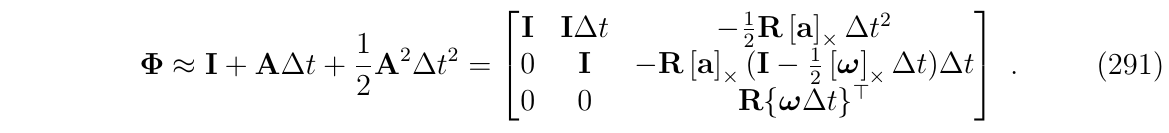
对于完整版IMU的例子
从系统矩阵A的次幂来看,在3阶之后,就没有非零项消失和产生,因此,取3阶进行截断,得到:
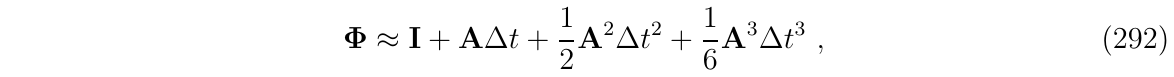
具体的矩阵展开,可往前面翻.
4.2. Block-wise截断(这个好用)
这是一种与前面所推导的闭式结果相当接近的近似方法是: 对状态转移矩阵\(\Phi\)的每个块的泰勒级数展开的第一个有效项上进行截断
就是说,我们单独检查转移矩阵的每个非零子块,而不是对整个状态转移矩阵的泰勒展开序列进行截断。因此,需要在每个块的基础上分析截断
下面使用两个例子来讨论:
4.2.1. 简化版IMU例子
对于\(\Phi_{v,\theta},\Phi_{p,\theta}\)项,分别有序列\(\Sigma_1\)和\(\Sigma_2\)
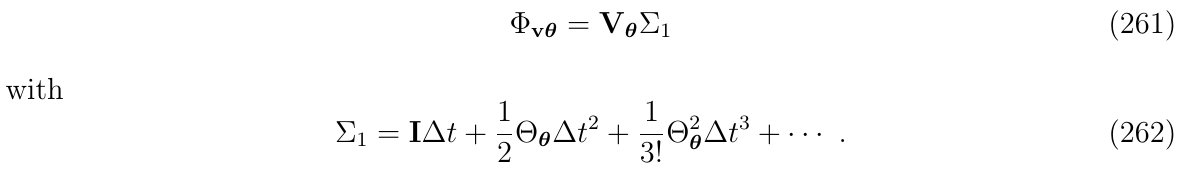
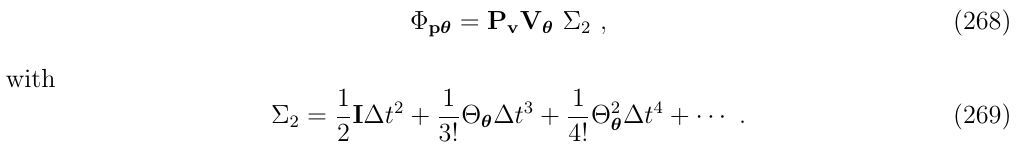
对上述序列\(\Sigma_1\)和\(\Sigma_2\)进行1阶截断,得到:
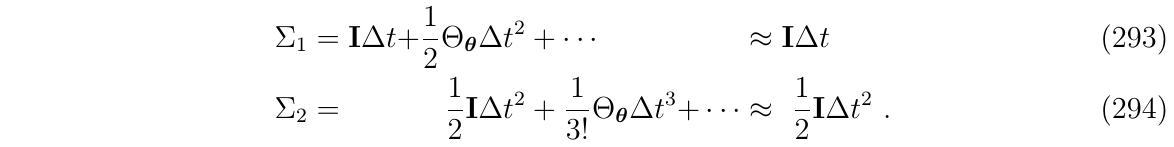
于是,简化版IMU系统的状态转移矩阵\(\Phi\)可近似如下:
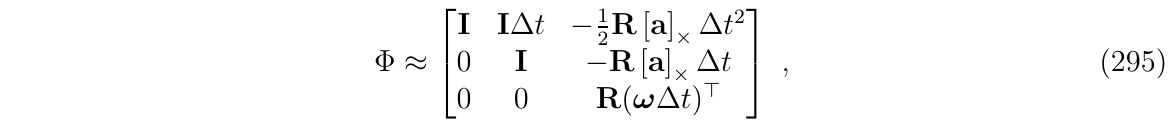
这种截断方法比上面的全系统(system-wide)一阶截断法更精确,同时,特别是与封闭形式相比,又很容易获得和计算。
对于右下角(3,3)项,由于其闭式已经计算出来了,而且比较好计算,所以直接使用闭式形式即可。
4.2.2. 完整版IMU例子
对于完整的IMU系统,将前面所推导的\(\Sigma_n\)代入到状态转移矩阵\(\Phi\)中,然后进行截断,可以得到转移矩阵的近似:
(1)标准的状态转移矩阵\(\Phi\):
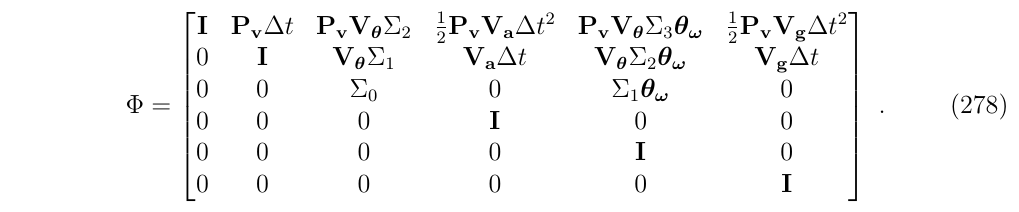
- \(P_v=I\)
- \(V_\theta=-R[a_m-a_b]_\times\)
- \(V_a=-R\)
- \(V_g=I\)
- \(\Theta_{\theta}=-[w_m-w_b]_\times\)
- \(\Theta_w=-I\)
(2)\(\Sigma_n\)的闭式表达:

(3)根据上面的推导进行截断,得到
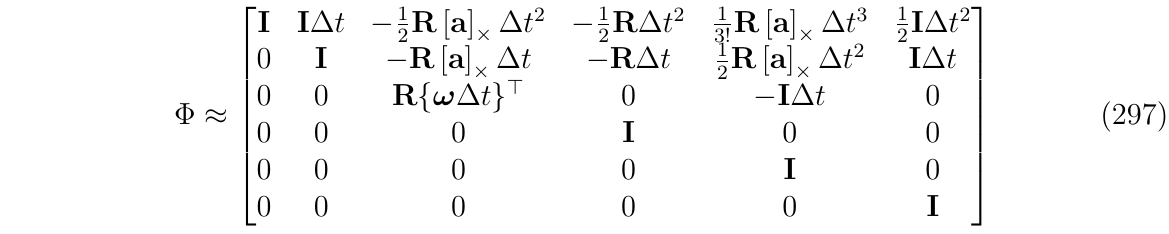
其中,
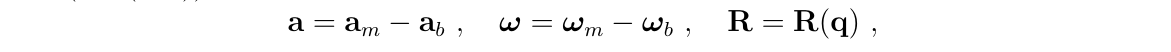
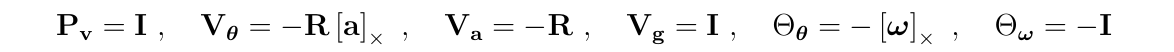
(4)如果还想要进一步简化,一个直接的方法是限制每个子块的最高阶数n
当n=1(也就是欧拉法),我们得到:
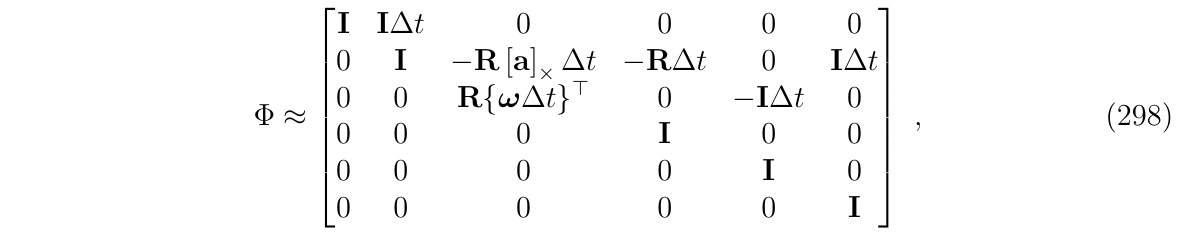
当n=2,我们得到:
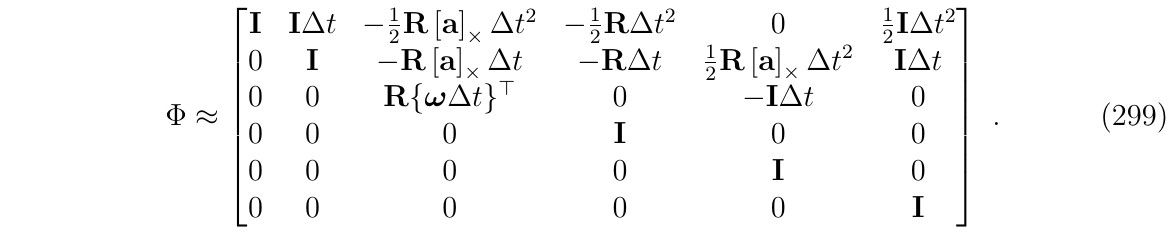
当n=3,也就是最上面的(式297)了
5. 使用龙格库塔积分法得到状态转移矩阵(时变)
其他方法来近似得到状态转移矩阵就是使用龙格库塔积分法,当动态矩阵(系统矩阵)A在积分区间内不能被认为是常数的情况下(即系统矩阵是时变的矩阵\(A(t)\)),这是可能可以使用。
假设有连续时间系统:
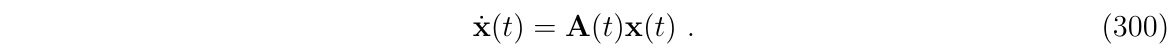
让我们重写以下两个关系,它们在连续时间和离散时间中定义了同一个系统,这分别包含了时变的系统矩阵\(A(t)\)和状态转移矩阵\(\Phi\):
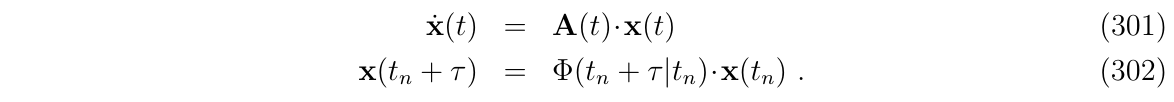
上面两个等式可以分别以两种方式推导\(\dot{x}(t_n+\tau)\)
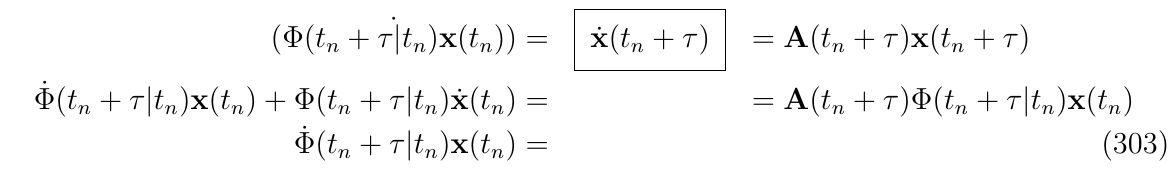
其中,需要注意的是\(\dot{x}(t_n)=\dot{x}_n=0\),因为这是采样得到的值。
于是,得到:
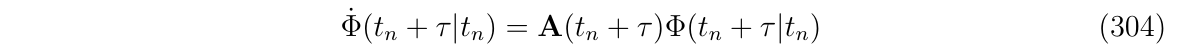
得到了一个与(式303)一样的常微分方程[即自变量只有1个的微分方程],只不过是使用转移矩阵\(\Phi\)替换掉了(式303)里面的状态向量。
注意到,因为在起始时系统满足\(x(t_n)=\Phi_{t_n|t_n}x(t_n)\),所以有:
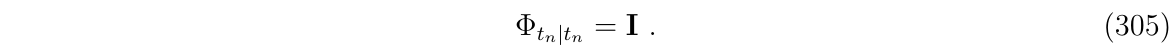
对非线性函数\(f(t,\Phi(t))\)使用RK4积分,我们得到:
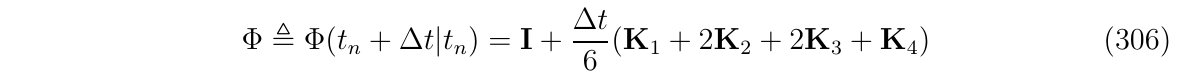
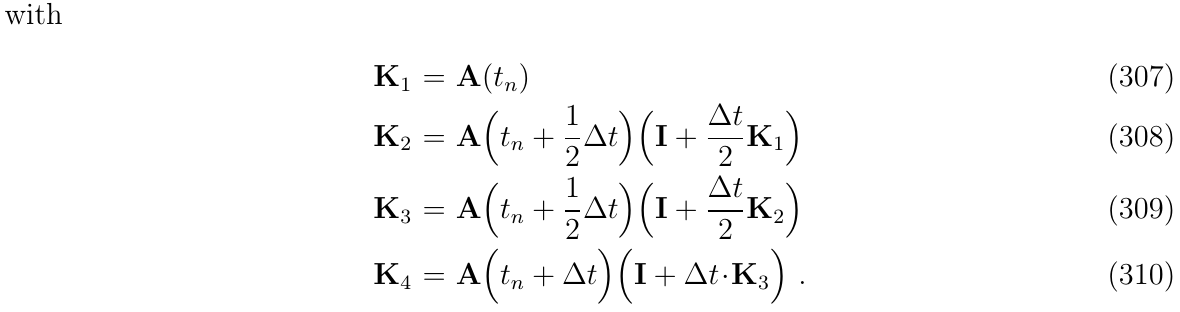
5.1. 举例: 误差状态方程
现在,考虑一个对于一个非线性,时变的系统使用误差状态卡尔曼滤波器(eskf):
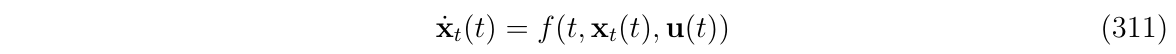
其中,\(x_t\)代表了状态真值,\(u\)代表控制输入,真值是由nominal状态\(x\)和误差状态\(\delta\)的组合:
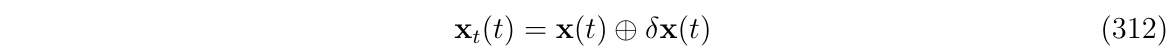
误差状态方程使用线性表达形式,该系统矩阵A由时变的向量(nominal状态\(x\)和输入控制量\(u\))来决定:
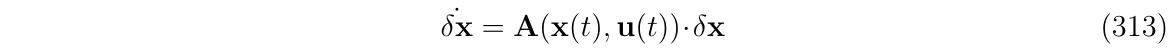
那么,根据(式304)的推导,对应的状态转移矩阵形式可写成如下:
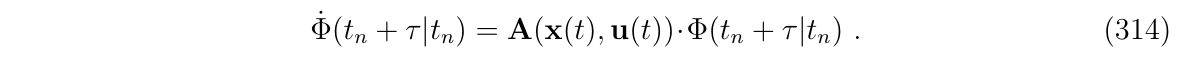
为了对此等式使用RK积分,我们需要计算\(x(t)\)和\(u(t)\)在RK积分处的值,如果使用RK4来积分,那么就是\(\{t_n,t_n+\frac{\Delta t}{2},t_n+\Delta t\}\)这几个时间点
从简单的开始,积分点处的控制输入\(u(t)\)可以通过当前\(u_n\)和最后一次测量值\(u_{n+1}\)进行线性插值得到,即:
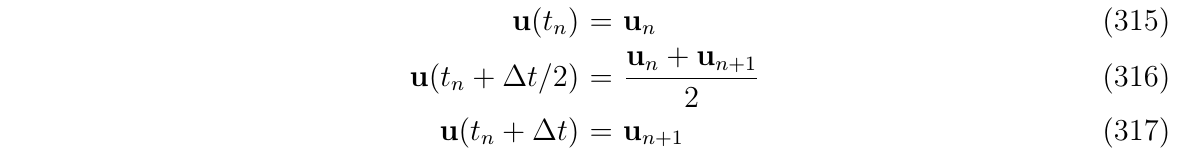
Nominal state方程应采用最优的方法进行积分,例如,使用RK4:
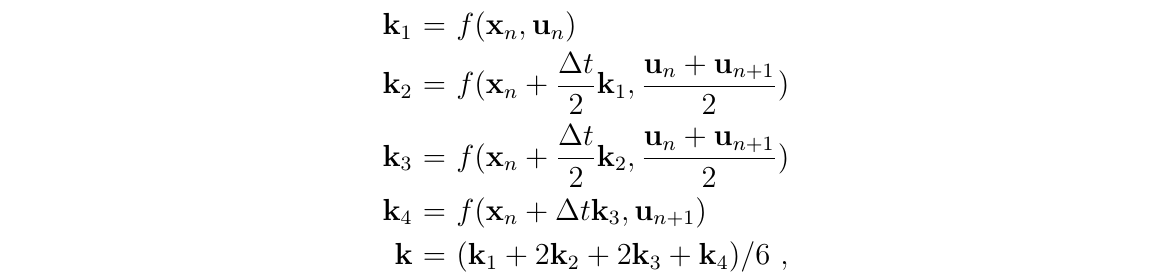
这里的函数\(f()\)指的是\(x_t(t)\)的导数,是时变的,即(式311)
通过计算加权得到的\(k\),我们可以得到积分处点的状态值的积分估计:
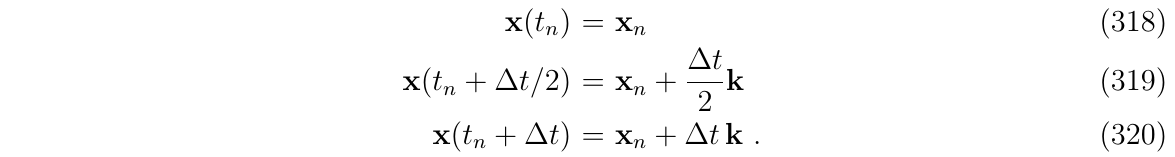
我们注意到: \(x(t_n+\frac{\Delta t}{2})=\frac{x_n+x_{n+1}}{2}\),这和我们在输入控制\(u_t\)的计算中所使用的线性插值是一样的,考虑到RK更新的线性特性,这应该不足为奇。
无论我们以何种方式获得Nominal state状态值,我们现在都可以计算RK4矩阵来进行转移矩阵\(\Phi\)的积分: