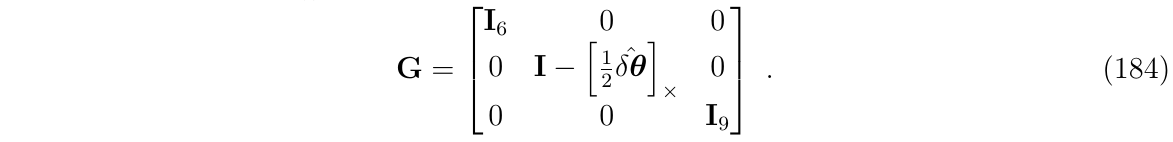1. 第一章 四元数
2. 第二章 IMU驱动系统的误差状态运动学
2.1. 动机
我们希望写出带有偏置和噪声的加速度计和陀螺仪读数中惯性系统运动学的误差位置方程,用哈密尔顿四元数表示空间方向或姿态。
误差状态卡尔曼滤波器 error-state Kalman filter (ESKF):
- 姿态误差最小(它有与自由度相同数量的参数),避免与过度参数化(或冗余)相关的问题以及所涉及的协方差矩阵的奇异性风险
- 误差状态系统总是在接近原点的地方运行,因此远离可能的参数奇异点, gimbal lock等问题,提供任何时候都有效保证的线性化
- 误差状态总是很小,意味着所有二阶项的影响都很小,这使得雅可比矩阵的计算非常简单和快速,一些雅可比矩阵甚至可以是常数,或者等于可用状态的大小。
- 误差动力学是缓慢的,因为所有大的信号都被整合成nominal-state。这意味着我们可以以比预测操作更低的速度进行更新(这是观察误差的唯一方法)
2.2. ESKF的解释
在eskf公式中,分为真值(true-),nominal-,和误差状态值(error-state values)。真实状态被表示为nominal-和误差状态值(error-state values)合适的组合(线性叠加,四元数乘积,矩阵乘法等)。这个思路是把nominal-state考虑为大信号(以非线性方式可积)以及把误差状态值作为小信号(因此线性可积,适用于线性高斯滤波)。
因此,eskf可以解释为如下:一方面,高频率的IMU数据\(u_m\)被整合(积分)成nominal-状态值\(x\),这个nominal-state不考虑噪声项\(w\)以及其他可能影响的模型参数。因此,这个norminal值会累积误差。这些errors被误差状态\(\delta x\)所收集,然后使用eskf来估计,此时这次加入了所有的噪音和干扰。误差状态由小信号组成,它的传递函数是由(时变)线性的[带有动态、控制和测量矩阵]的动态系统正确定义的。与nominal-state的积分平行,ESKF预测的是误差状态的高斯估计,而更新过程是由其他观测信号(IMU以外的如GPS,视觉路标)到达之后进行的。这种更新修正提供了误差状态的后验高斯估计,之后误差状态的均值被注入到nominal-state,然后将误差状态重置为0,然后更新误差状态的协方差矩阵。
2.3. 连续时间系统运动学
下面是一些定义:
- 角速度\(\omega\)被定义为相对于nominal-state是local的(The angular rates ω are defined locally with respect to the nominal quaternion),这允许我们直接使用角速度测量值\(\omega_m\),它提供了body系的角速度。
- 角度误差\(\delta \theta\)被定义为相对于nominal-state是local的,这未必是最佳的方式,但这与大多数imu积分过程中的选择是一致的(经典方法)。
- \(a_t\)是全局坐标系下的加速度真值
- \(a_m\)是测量得到的载体坐标系下加速度测量值(含有噪声和偏置)
2.3.1. 状态真值
运动学方程
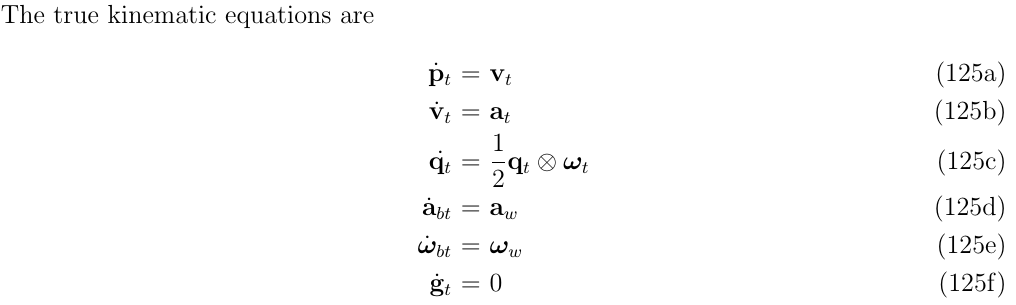
body坐标系下的加速度\(a_m\)和角速度\(w_m\)可以使用加速度真值\(a_t\)和角速度真值\(w_t\)以及噪声来表达:
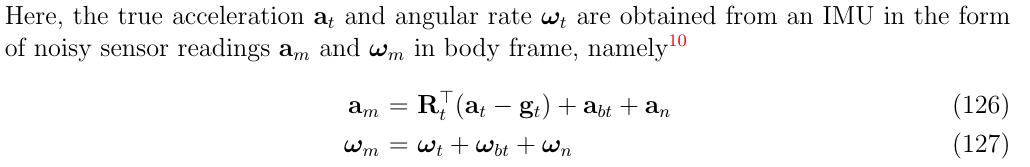

写成逆的形式
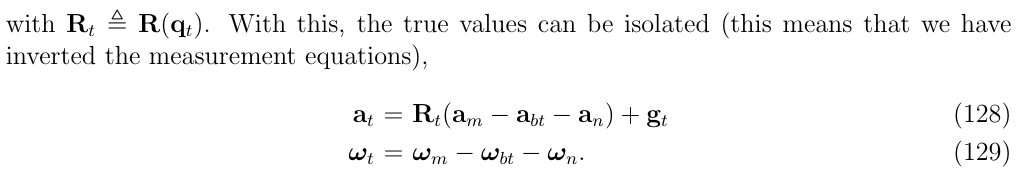
对上面这些式子进行整合,得到完整的运动系统

可以定义这个系统为\(\dot{x}_t=f_t(x_t,u,w)\),系统可以写成如下形式:
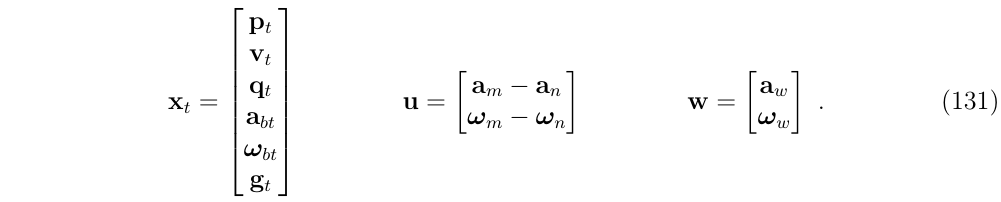
需要注意的是:
在上面的公式中,重力向量\(g_t\)将由滤波器来估计,它有一个恒定的演化方程(130f), 相当于一个已知的常数大小。系统从一个固定的和任意已知的初始方向开始\(q_t(t=0)=q_0\),(由于一般不在水平面上,使得初始重力矢量一般未知)。为了简单起见,通常采用以下这种方法: $q_0 = (1, 0, 0, 0) \(,因此有\)R_0=R{q_0}=I\(,然后我们估计重力向量\)g_t\(在\)q_0\(下的表示,而不是\)q_t$在水平坐标系中表达,因此,初始的方向不确定度转化为重力方向的初始不确定度。
我们这样做是为了提高线性度,现在式(130b)是关于\(g\)线性化的,携带所有的不确定性,而初始方向\(q_0\)是已知的(没有不确定性的),因此\(q\)的开始是不带有不确定性的。
一旦估计出重力矢量,就可以恢复水平面,恢复的运动轨迹可以重新定向,以反映估计的水平。
2.3.2. nominal-state kinematics
即没有噪声和扰动的模型

2.3.3. 误差状态
我们的目标是: 确定误差状态的线性化动力学,对于每个状态方程,在表格2中写出了它们的组合,求解误差状态,简化所有二阶无穷小,下面给出完整的误差状态动态系统,并在此基础上进行了讨论和证明。
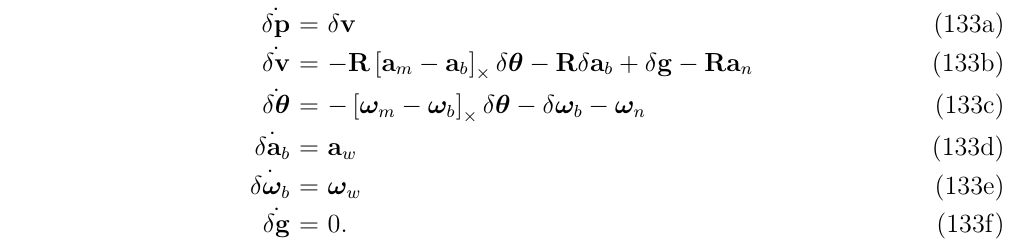
上面的等式(133a), (133d), (133e) and (133f),分别代表了位置,偏置和重力误差,是从线性方程推导出来的(即使用式130-式132得到的),它们的错误状态动态是微不足道的。
举例:考虑真值和nominal位置等式(130a) and (132a),它们的组合是\(p_t=p+\delta p\),然后计算出来的\(\delta \dot{p}\)就是式(133a)所示。
等式 (133b) and (133c),速度和方向误差,要求对非线性方程进行一些特别的处理(等式 (130b) and (130c) ),来获得线性化的方程。他们的证明将在以下两节中展开
Equation (133b): The linear velocity error的推导
我们希望确定\(\delta \dot{v}\)(速度的误差),从下面的等式开始
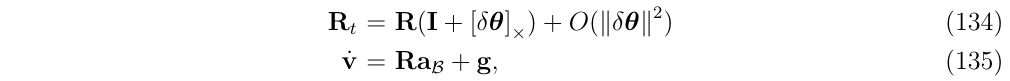
式(134)是对\(R_t\)的欧拉角近似,在式(135)中,我们重写\((132b)\),但是引入了\(a_{\mathcal{B}}\)和\(\delta a_{\mathcal{B}}\)来进行简写,其中
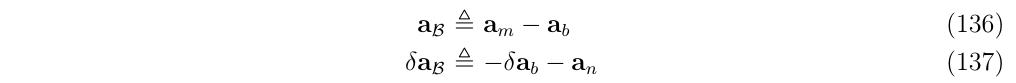
于是,我们可以写出在惯性坐标系i系的加速度真值:
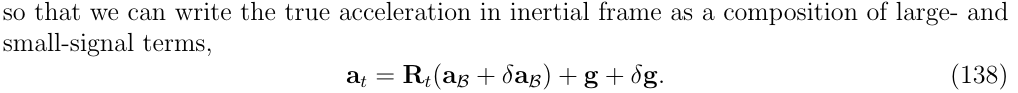
接下来,通过对式(130b)中\(\dot{v}_t\)写成两种形式,其中\(O(||\delta \theta||^2)\)被忽略:
因为\(\dot{v}_t=R_t a_t +g_t\),所以有下列等式的右侧
同时,又有\(\dot{v}+\dot{\delta v}=\dot{v}_t\),所以有下列等式左侧
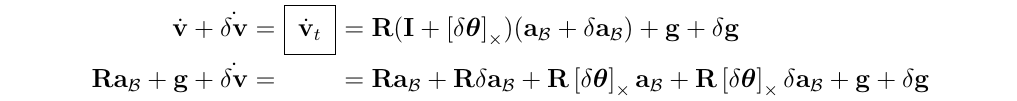
去掉等式两边的\(Ra_{\mathcal{B}}+g\),得到了:
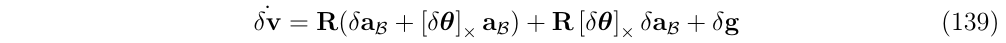
消去二阶项\(R[\delta \theta]_{\times}\delta a_{\mathcal{B}}\)以及对叉乘进行变换,得到:
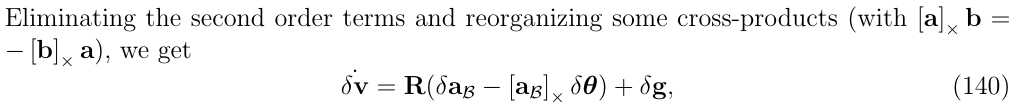
然后,把上面定义的变量\(a_{\mathcal{B}}\),\(\delta a_{\mathcal{B}}\)重新使用(136,137)使用原来定义的变量
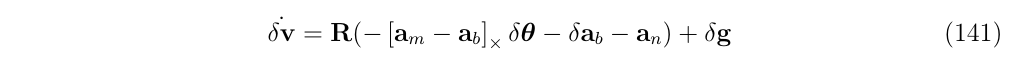
这就是最前面的(式133b)的推导:
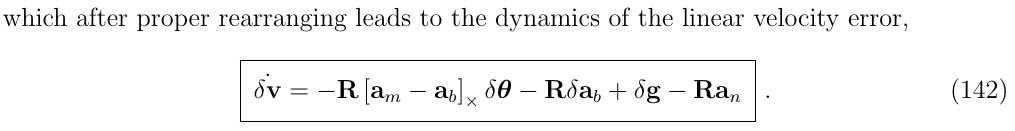
为了进一步简化这个表达,我们通常假设加速度噪声是白噪声,独立的,(也就是看做是均值为0的高斯分布)
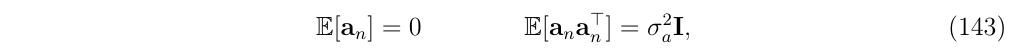
协方差椭球是一个以原点为中心的球体,这意味着它的均值和协方差矩阵在旋转时不变,证明如下:

然后我们可以重新定义加速度计的噪声矢量,绝对没有任何后果
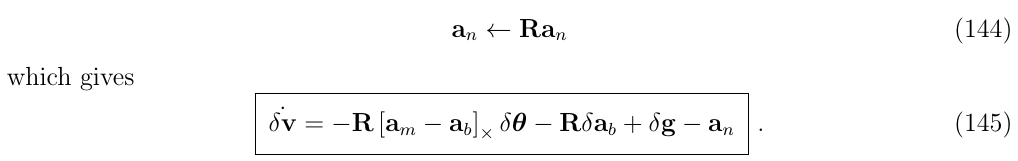
Equation (133c): The orientation error. 姿态误差的推导
我们希望确定角度误差\(\delta \dot{\theta}\)的表达式,从下面的两个关系式开始:
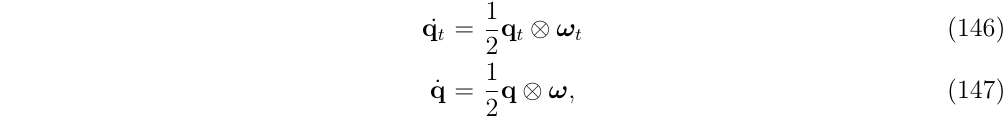
跟前面加速度的处理一样,先对角速度进行简化表达:
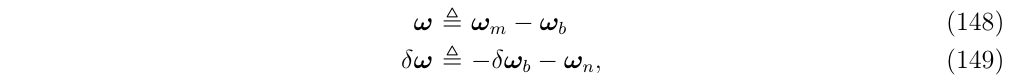
那么,角速度真值\(w_t\)可以写成
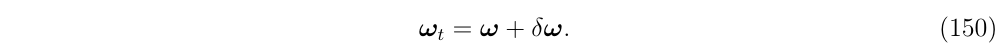
然后使用两种不同的表达来表示\(\dot{q}_t\)
因为\(q_t=q \otimes \delta q\),于是有\(\dot{q}_t = \dot{(q \otimes \delta q)}\)
所以:
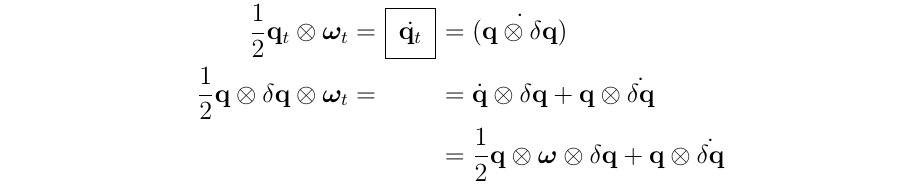
接着:
(1)去掉q(即对上式两边同时乘以2,然后把\(\frac{1}{2}q\otimes w \otimes \delta q\)移到左侧,然后再把q去掉)
(2)并且对\(\dot{\delta q}\)进行分离(使用四元数乘法的两种算法(左乘和右乘)) ,然后得到:
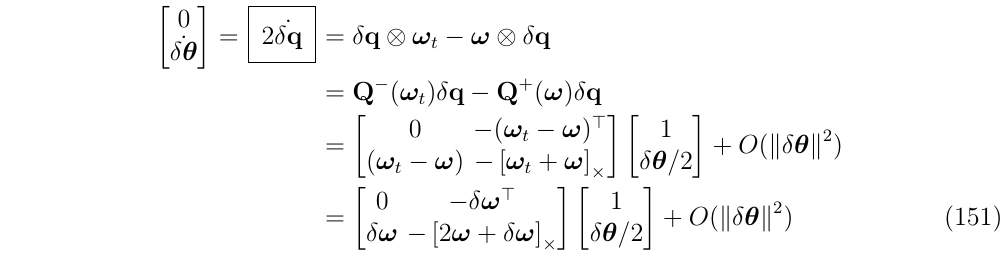
结果得到一个标量和一个向量的等式
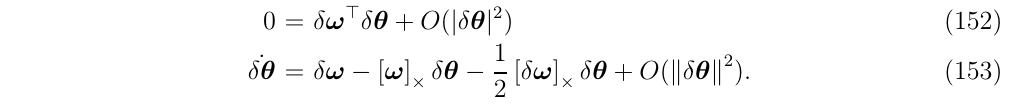
第二个等式,进一步去除2阶项之后,得到
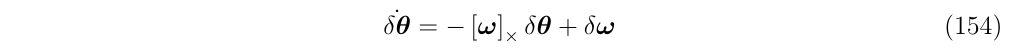
最终,把中间变量\(w\)和\(\delta w\)换回原来的变量,得到:
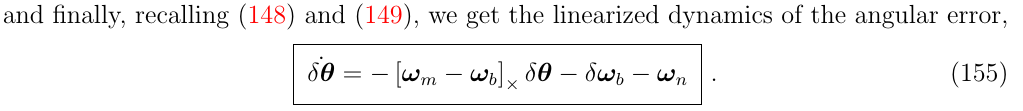
2.4. 离散时间的系统
上述微分方程需要集成(积分)到差分方程中,以考虑离散时间间隔t > 0,积分的方法有很多,在某些情况下,可以使用完全封闭的解,在其他情况下,可以采用不同精度的数值积分。
需要对以下子系统进行积分:
nominal state
error-state
(1)确定性部分:状态动力学和控制 (2)不确定部分:噪声和扰动
2.4.1. nominal state 方程
差分形式如下
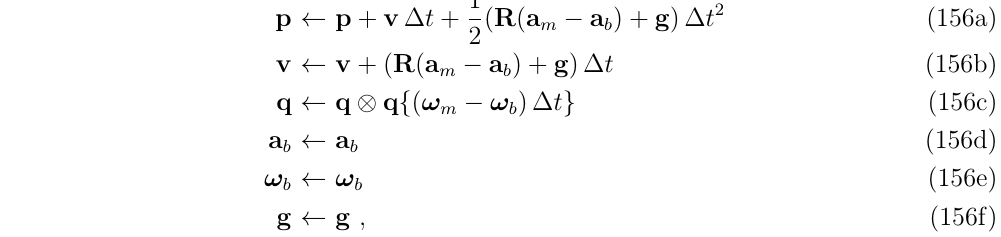
其中,\(R \triangleq R\{q\}\)是与当前nominal state的q相关的旋转矩阵,\(q\{v\}\)是与旋转向量v相关的四元数,如下

当然,上面的差分形式中的积分部分可以使用其他更加精确的积分,具体见附录。
2.4.2. 误差状态方程
回顾连续时间下的误差状态方程:
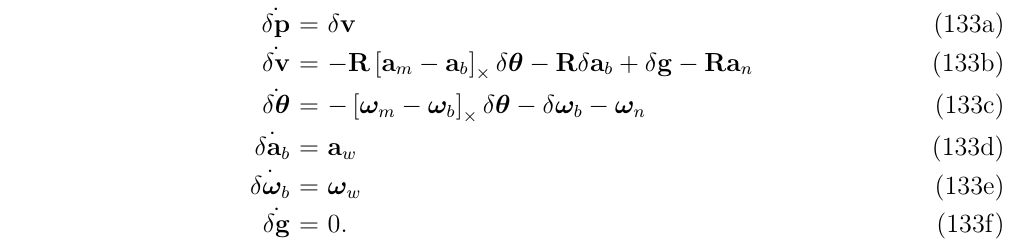
对连续时间下使用时间步\(\Delta t\)进行积分,得到离散时间下的误差状态方程
转换规则:
- 对于确定性的部分,可以使用积分法(也就是附录 C.2 )
- 对于不确定性的部分,使用产生随机脉冲 (见附录 E)
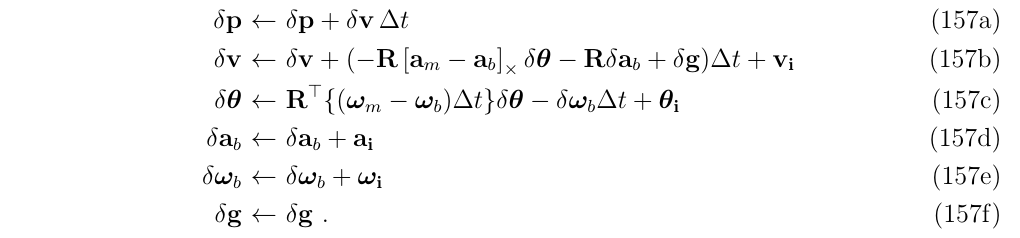
(式157c)的\(\delta \theta\)的怎么推导的?
推导如下:
(1)暂时忽略掉一些误差项,只保留\(\dot{\delta \theta}=-[w]_\times \delta \theta\)
(2)对这个微分方程进行求解,可以得到:
\[ \begin{aligned} \delta \theta_{k+1}= \Phi \delta \theta_{k} = e^{-[w]_\times \Delta t} \delta \theta_{k} \end{aligned} \]
(3)将转移矩阵\(\Phi\)进行泰勒级数展开:
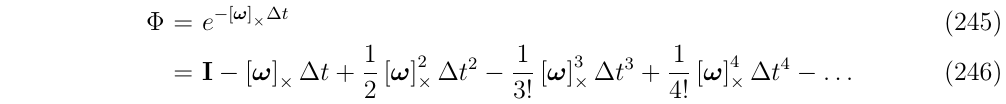
(4)根据式53,可以写成罗德里格斯公式,最终状态转移矩阵\(\Phi\)化简为关于\(-w\Delta t\)的旋转矩阵,即:
\[ \Phi=R\{-\boldsymbol{u} \Delta \theta \}=R\{-\boldsymbol{w} \Delta t\}=R\{\boldsymbol{w} \Delta t\}^T \]
所以,得到
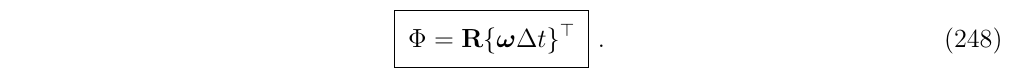
最后再补上误差和扰动项,就得到了(式157c)的结果
上面的离散时间下的误差状态方程中,\(v_i,\theta_i,a_i,w_i\)都是应用于速度,角度,偏置估计的随机脉冲,使用高斯白噪声模型,它们的均值都是0,协方差矩阵是通过对\(a_n,w_n,a_w,w_w\)在一个时间步(即\(\Delta t\))内的积分(见附录 E),即:
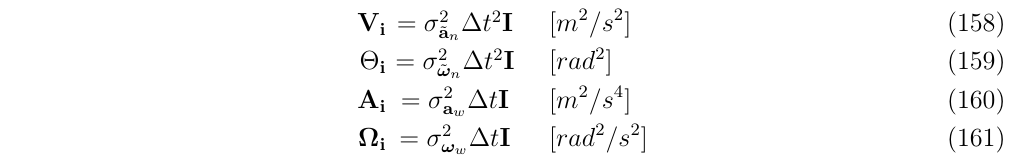
其中,\(\sigma_{\tilde{a}_n}[m/s^2],\sigma_{\tilde{w}_n}[rad/s],\sigma_{\tilde{a}_w}[m/s^2 \sqrt{s}],\sigma_{\tilde{w}_w}[rad/s \sqrt{s}]\)可以通过IMU的出厂数据或者通过标定实验得到。
2.4.3. 误差状态的雅克比和扰动矩阵
通过对前一节中误差状态差分方程的简单检验,得到了雅可比矩阵
为了把这些方程写成紧凑的形式,我们考虑使用 nominal-state向量\(x\),误差状态向量\(\delta x\),输入向量\(u_m\)和扰动脉冲向量\(i\)(see App. E.1 for details and justifications),这些向量展开如下:
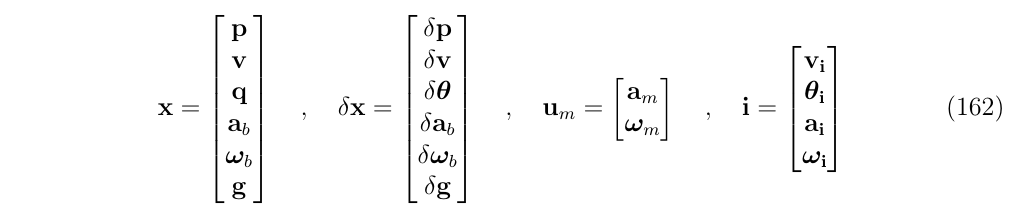
此时,误差状态系统可以写成:
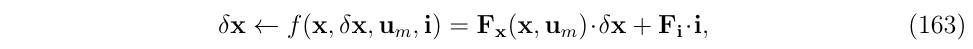
ESKF预测等式可以写成:
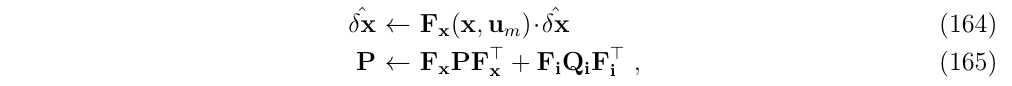
其中,
- \(\delta x \sim \mathcal{N}\{\hat{\delta x},P\}\);
- \(F_x\)和\(F_i\)是f()分别对误差和扰动的雅克比;
- \(Q\)是扰动脉冲的协方差矩阵
下面详细介绍上面的雅可比矩阵和协方差矩阵的表达式,这里出现的所有与状态相关的值都是直接从normal-state中提取的:
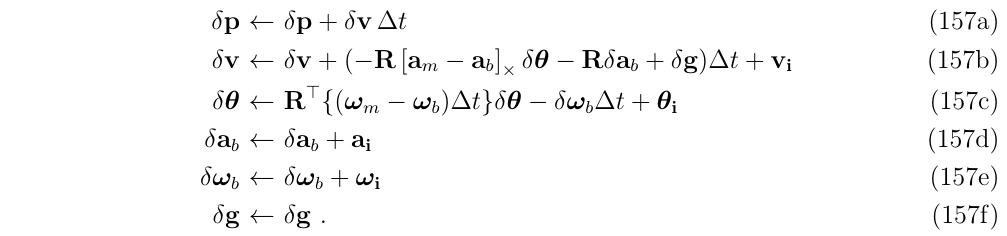
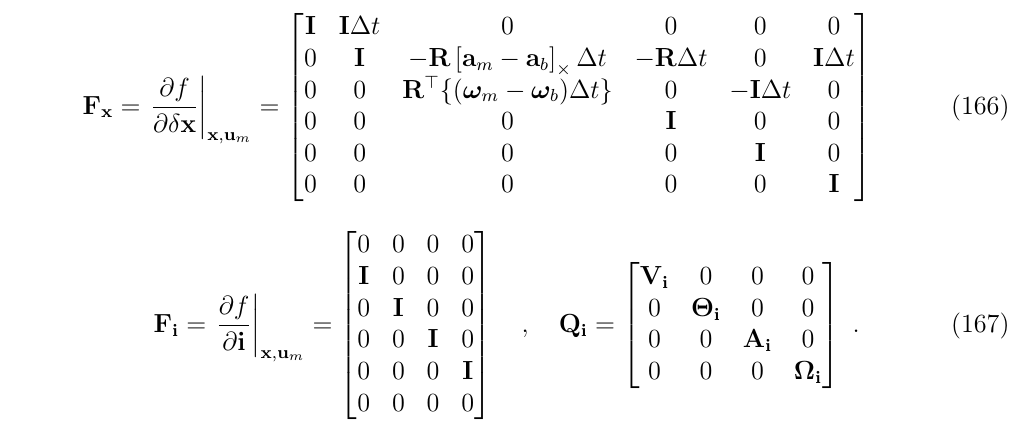
特别需要注意的是:
\(F_x\)是系统的转移矩阵,可以使用多种方法来近似到不同级别的精确度。在这里使用了比较简单的欧拉法进行近似(Euler form)
另外,还需要注意的是,如果误差\(\delta x\)被初始化为0,于是线性化等式(164)一直返回0,当然,您应该跳过代码中的关于(164),我建议你把它写下来,但是你要把它注释掉,这样你就可以确定你没有忘记任何东西。
请注意,最后,你不应该跳过协方差预测(165),实际上,\(F_iQ_i F_i^T\)不是空的,因此它的协方差应该是一直增长的——在任何预测步骤中都是如此。
3. 使用互补的传感器数据融合IMU
当其他类型的传感器数据(GPS,Vison)到达,我们使用ESKF进行处理。在一个设计好的系统中,这将使IMU的偏差变得明显,然后允许ESKF来正确的估计这个误差。
最常见的有GPS+IMU,单目+IMU,双目+IMU,近年来,使用IMU和视觉传感器融合领域引人注目,使用视觉+IMU对于在不能使用GPS的环境中十分有趣,可以在移动设备(手机)、无人机等其他平台上使用。
在上面的讨论中,IMU信息到目前为止一直用于对ESKF进行预测,而其他的传感器信息用于矫正滤波器,矫正分为3个步骤:
- 通过滤波器校正对误差状态的观测
- 注入观测误差到 nominal state
- 重置误差状态
3.1. 第一步: 通过滤波器校正对误差状态的观测
假设像往常一样,我们有一个传感器,它所传输出来的信息依赖状态真值:
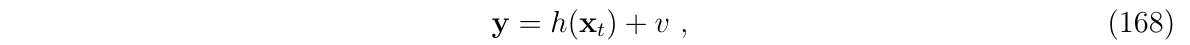
其中,h()是关于状态真值的非线性函数的一般形式,\(v\)是协方差为\(V\)的高斯白噪声:
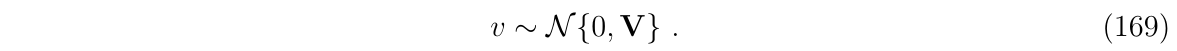
我们的滤波器是先估计误差状态,然后有滤波器校正方程:
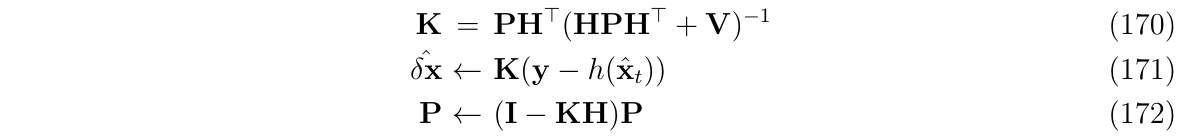
其中,需要:
- 状态误差\(\delta x\)的雅克比矩阵\(H\),
- 使用校正之后的状态误差最优估计\(\hat{\delta x}\),对状态真值估计进行更新,即\(\hat{x_t}=x \oplus \hat{\delta x}\)。
由于此时的误差状态均值为零(我们尚未观测到),因此,我们此时只能得到\(\hat{x_t}=x\),我们可以使用nominal error x作为线性化点,得到雅克比矩阵\(H\):
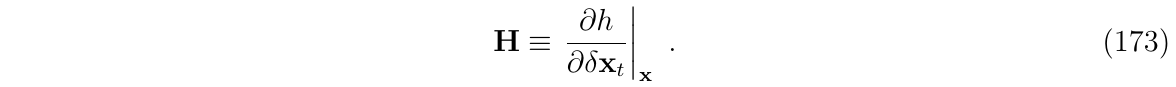
上面给出了协方差更新的最简单的形式:\(P\leftarrow (I-KH)P\),但是这种形式的数值稳定性很差,因为它的结果不一定是对称的,也不一定是正定的。一般可以使用更稳定的形式,如
- the symmetric form: \(P\leftarrow P-K(HPH^T+V)K^T\)
- the symmetric and positive Joseph form: \(P\leftarrow (I-KH)P(I-KH)^T+KVK^T\)
3.1.1. 计算观测矩阵H
上面的观测矩阵可以用多种方法计算,最常用连式法则:
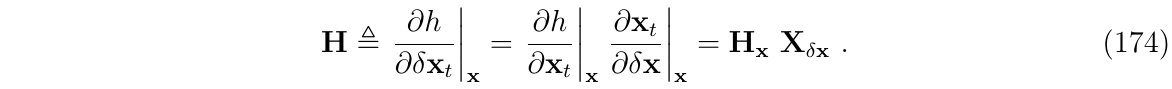
其中,\(H_x \triangleq \frac{\partial h}{\partial x_t}|_x\)是关于函数h()的分别对其参数的雅克比
第一部分\(\frac{\partial h}{\partial x_t}|_x\)由传感器的测量函数决定,这里不具体展开
第二部分\(X_{\delta x}\triangleq \frac{\partial x_t}{\partial \delta x}|_x\)是状态真值对于误差状态的雅克比,这部分可以在这里导出,因为它只依赖于状态的ESKF组合,因此,有:
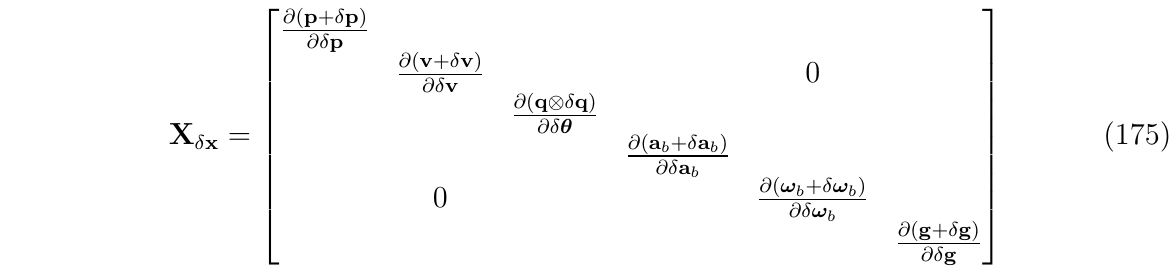
对上面进行分块,简化,得到:
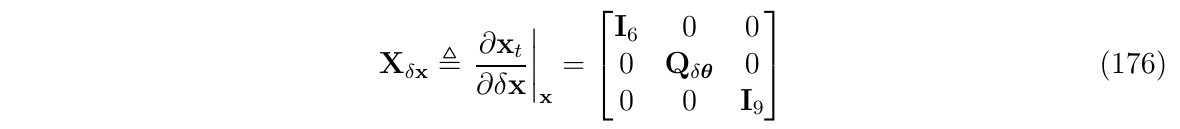
其中,\(Q_{\delta \theta}=\frac{q\otimes \delta q}{\delta \delta \theta}\)是\(4\times 3\)的矩阵块,使用(式14/15)以及一阶近似(\(\delta q \rightarrow [1 , \frac{1}{2}\delta \theta]^T\) , 见下方补充),那么\(Q_{\delta \theta}\)可以写成:
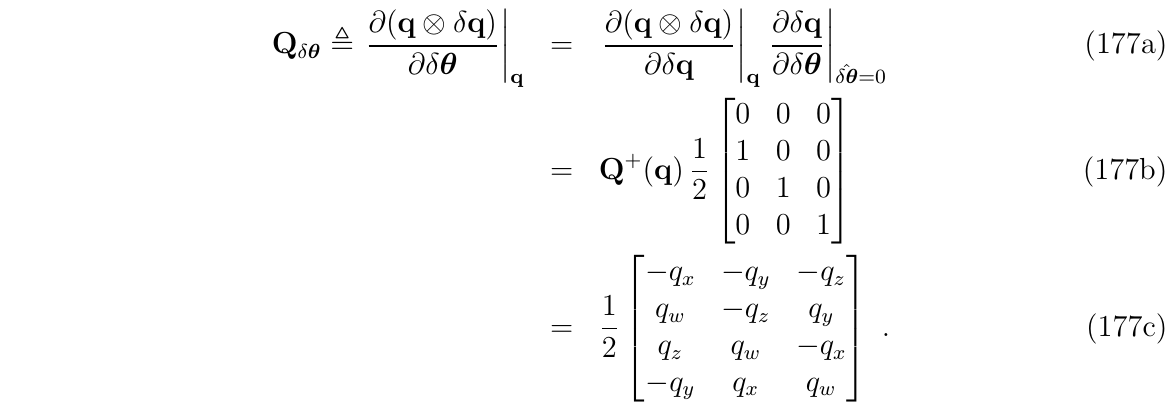
补充:

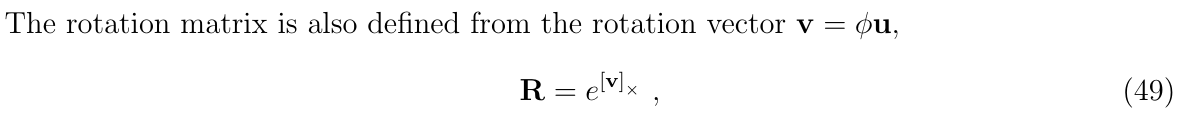
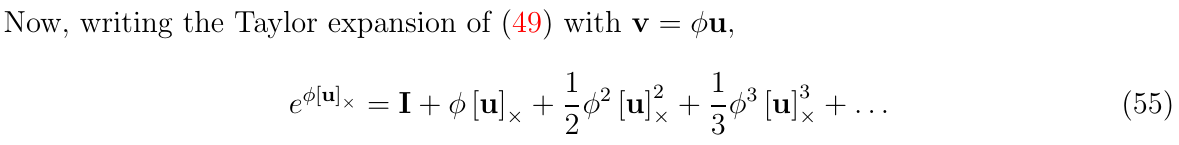

上面的意思是: 当给定旋转向量\(\delta \theta\),其四元数为:
\[ \begin{aligned} \begin{bmatrix} \cos(\frac{\delta \theta}{2}) \\ I_{3\times 1}\sin(\frac{\delta \theta}{2}) \end{bmatrix} \end{aligned} \]
当\(\theta\)很小时,有\(\frac{\delta \theta}{2}=\sin(\frac{\delta \theta}{2})\)和\(\cos(\frac{\delta \theta}{2})=1\)
所以有:
\[ \begin{aligned} \delta \leftarrow \begin{bmatrix} 1 \\ \frac{1}{2}\delta \theta \end{bmatrix} \end{aligned} \]
或者使用泰勒展开,取一阶近似,也是可以得到相同的结果
3.2. 第二步: 注入观测误差到 nominal state
经过ESKF更新校正之后,可以使用校正之后的误差状态\(\hat{\delta x}\)与nominal state组合,得到状态真值的估计:
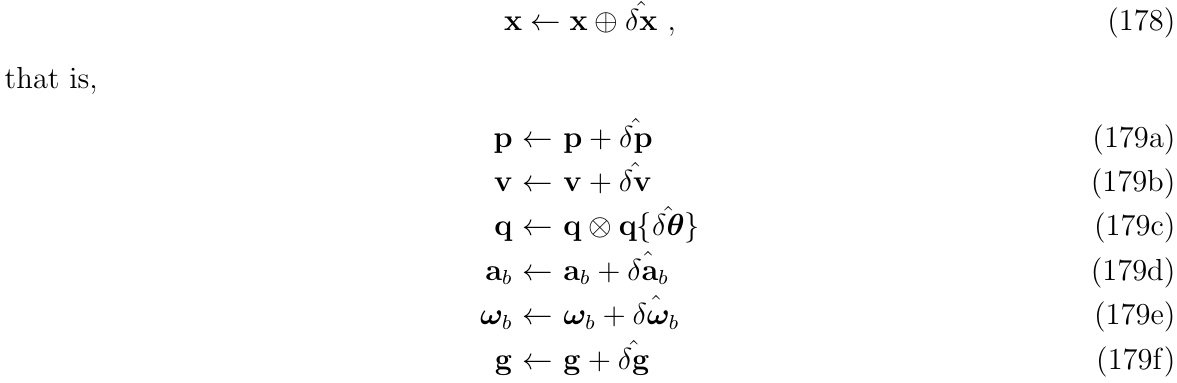
3.3. 第三步: ESKF重置
(为什么需要重置? 你都观测到接近真值了,并且进行了校正,误差状态当然要重置啊)
当所有误差状态注入到nominal state之后,误差状态均值\(\hat{\delta x}\)需要被重置,尤其是旋转的部分,因为新的旋转姿态误差是相对于新的nominal state的姿态坐标系而言的。
为了ESKF完整更新,误差状态的协方差也需要被更新
下面称误差重置函数为\(g()\),即:
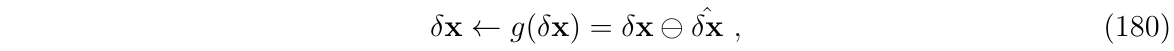
其中,\(\ominus\)表示与\(\oplus\)相反的操作,因此,ESKF重置操作可表示为:
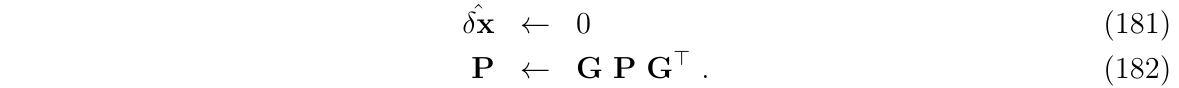
其中,矩阵G为:
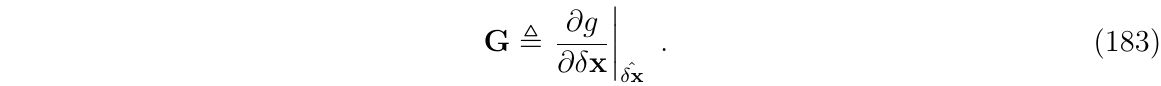
与在第一步中的雅克比矩阵类似,这个矩阵对角线上的子块,除了与旋转部分有关,其他都是单位矩阵I