- 1. 1. 运动分析的数学实质
- 2. 2. 零输入响应和零初态响应的定义
- 3. 3. 连续时间线性时不变系统的运动分析
- 4. 4. 连续时间线性时不变系统的状态转移矩阵
- 4.1. 4.1. 基本解阵
- 4.2. 4.2. 状态转移矩阵
- 4.2.1. 4.2.1. 状态转移矩阵和基本解阵的关系()
- 4.2.2. 4.2.2. 状态转移矩阵的形式
- 4.2.3. 4.2.3. 状态转移矩阵用于零输入、零响应、全响应
- 4.2.4. 4.2.4. 求解状态响应
- 4.2.5. 4.2.5. 求解输出响应
- 4.2.6. 4.2.6. 状态转移矩阵的性质
- 4.2.6.1. 4.2.6.1. \(\Phi(0)=I\)
- 4.2.6.2. 4.2.6.2. \(\dot{\Phi}(t)=A\Phi(t)=\Phi(t)A\)
- 4.2.6.3. 4.2.6.3. \(\Phi(t_1+t_2)=\Phi(t_1)\Phi(t_2)=\Phi(t_2)\Phi(t_1)\)
- 4.2.6.4. 4.2.6.4. \(\Phi^{-1}(t)=\Phi(-t),\Phi^{-1}(-t)=\Phi(t)\)
- 4.2.6.5. 4.2.6.5. \(\Phi(t_2-t_0)=\Phi(t_2-t_1)\Phi(t_1-t_0)\)
- 4.2.6.6. 4.2.6.6. \(\Phi(kt)=[\Phi(t)]^{k}\)
- 4.2.6.7. 4.2.6.7. \(A=\Phi(0)\)
- 4.2.6.8. 4.2.6.8. 其他
- 5. 5. 连续时间线性时不变系统的脉冲响应矩阵
- 6. 6. 连续时间线性[时变]系统的状态转移矩阵
- 7. 7. 连续时间线性[时变]系统的离散化形式
- 8. 8. 连续时间线性[时不变]系统的离散化形式
1. 运动分析的数学实质
线性系统的状态方程为:
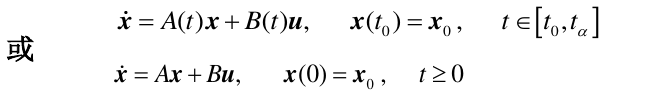
数学实质是:
相对于给定的初始状态\(x_0\)和外部输入\(u\),求解出状态方程的解\(x(t)\),即由初始状态和外输入作用所引起的状态响应。
2. 零输入响应和零初态响应的定义
利用线性系统的叠加原理,可以把系统在初始状态和输入控制向量作用下的运动分解为:
- (1) 由初始状态引起的自由运动
- (2) 输入作用引起的强迫运动
2.1. 零输入响应

2.2. 零初态响应

2.3. 系统总的运动响应
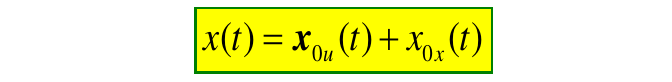
3. 连续时间线性时不变系统的运动分析
3.1. 前提内容——矩阵指数函数的计算
关于nxn的矩阵A的矩阵指数函数定义如下:
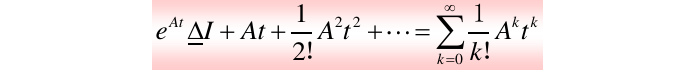
上面的三角等于号应该是等于号
3.1.1. 方法一:定义法
直接利用矩阵指数函数的定义式计算,即
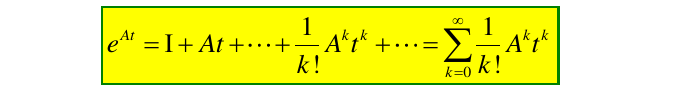
3.1.1.1. 矩阵A为对角线矩阵

3.1.1.2. 矩阵A为零幂矩阵
零幂矩阵: 即自乘若干次后化成零矩阵
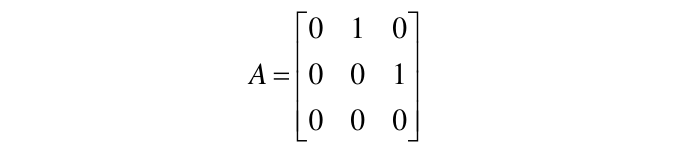

推广到N阶方阵
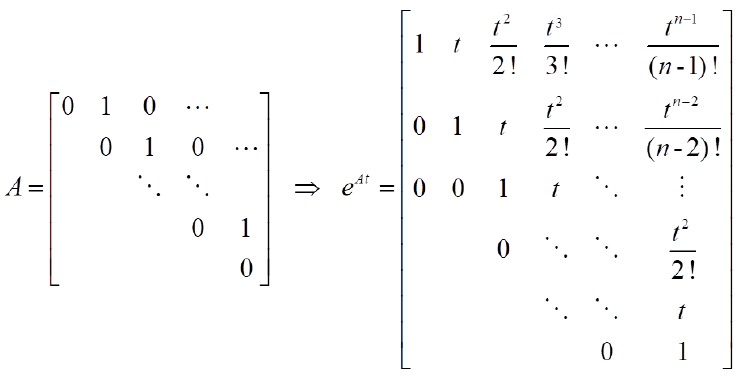
3.1.1.3. 矩阵A具有类似反对称形式

举例:

3.1.2. 方法二:特征值法
3.1.2.1. 矩阵A特征值两两互异
对矩阵A进行特征值分解,得到\(A=P\Lambda P^{-1}\),其中\(P=[v_1 , v_2 ,\cdots , v_n]\)是由特征向量(列向量)组合得到的.
因此,关于矩阵A的矩阵指数为:
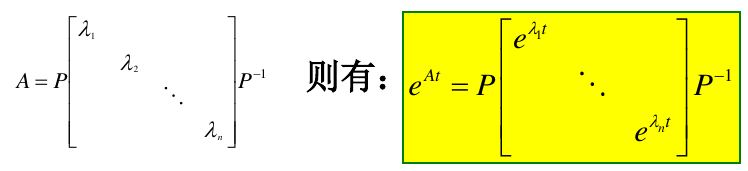
举例:


3.1.2.2. 矩阵A的特征值有重根时
回顾约旦规范型\(J=Q^{-1}AQ \Longrightarrow A=QJQ^{-1}\),因此,矩阵A的矩阵指数为:
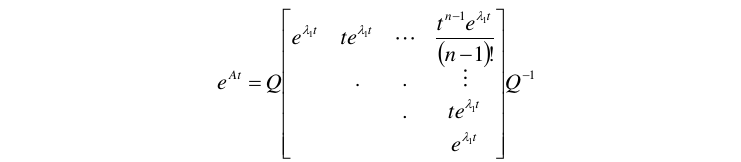
例子:

3.1.3. 方法三:有限项展开法
利用凯莱哈密顿定理(Cayley—Hamilton)化\(e^{At}\)为A的有限项
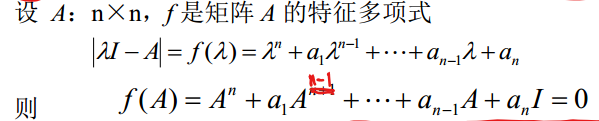
关于凯莱哈密顿定理的使用:

对\(e^{At}\)使用凯莱哈密顿定理,可得:
\[ e^{At}=\alpha_0(t)I+\alpha_1(t)A+\cdots+\alpha_{n-1}(t)A^{n-1} \]
即问题转换为求解这些\(\alpha\)的值
3.1.3.1. 情况1: 矩阵A的特征值互异
\(\alpha\)求解结果如下:

3.1.3.2. 情况2: 矩阵A有重根(n重特征值\(\lambda_1\))
\(\alpha\)求解结果如下:
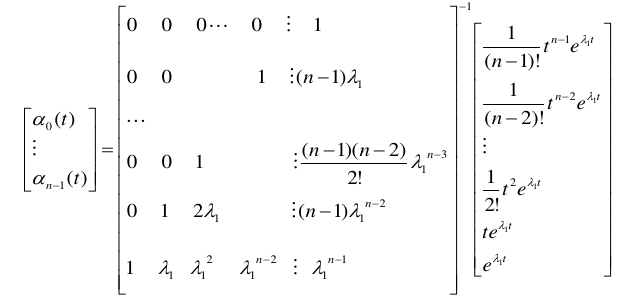
3.1.4. 方法四:预解矩阵法(拉氏反变换法)[好用]
对于给定的nxn常矩阵A,其指数函数满足:
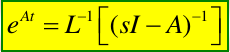

例子:


3.1.5. 矩阵指数函数性质
- \(\lim_{t \rightarrow 0} e^{At}=I\)
- \((e^{At})^T=e^{A^Tt}\)
- 令\(t\)和\(\tau\)为两个自变量,则\(e^{A(t+\tau)}=e^{At}\cdot e^{A\tau}=e^{A\tau}\cdot e^{At}\)
- \((e^{At})^{-1}=e^{-At}\)
- 设有\(n\times n\)常矩阵A和F,如果A和F是可交换的(即\(AF=FA\)),则有:\(e^{(A+F)t}=e^{At}\cdot e^{Ft}=e^{Ft}\cdot e^{At}\)
- \(\frac{d}{dt}e^{At}=Ae^{At}=e^{At}A\)
- \((e^{At})^m=e^{A(mt)}\)
3.2. 求解系统状态的零输入响应
输入u = 0时,线性定常系统的状态方程:
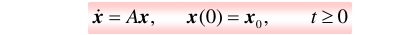
称为齐次状态方程。求线性定常系统的零输入响应,其实就是求该齐次状态方程的解
对上述微分方程进行求解,可得:
由状态方程\(\dot{x}=Ax\) 且 \(x(0)=x_0\),当\(t\geq0\)时,零输入响应为:
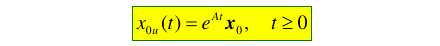
由状态方程\(\dot{x}=Ax\) 且 \(x(t_0)=x_0\),当$tt_0 , t_0 $时,零输入响应为:
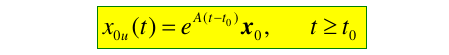
- 零输入响应的形态
- 在给定初态下,系统的零输入响应即系统在自由运动下的轨迹仅由矩阵指数函数\(e^{At}\)决定
- 矩阵指数函数即系统矩阵A包含了零输入响应即自由运动形态的全部信息
- 零输入响应的几何特征
- \(x(t)=e^{At}x_0\)说明系统在t时刻的状态点几何上可由初始状态点x0经过线性变换\(e^{At}\)得到
- 零输入响应随时间t演化过程,几何上即为状态空间中由初始状态x0出发,经过各个时刻变换点x(ti)所构成的一条轨迹
- 零输入响应趋向平衡态x=0属性
- 在没有外部输入下,系统的响应应该最终趋向平衡态x=0
- 系统的零输入响应即自由运动轨迹趋于x=0的条件为: \(\lim_{t \rightarrow \infty} e^{At}=0\)
3.3. 求解系统状态的零初态响应
由状态方程\(\dot{x}=Ax+Bu\) 且 \(x(0)=x_0\),\(t\geq0\)时,所描述的线性定常系统的零状态响应为:
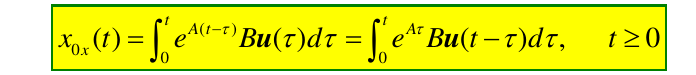
由状态方程\(\dot{x}=Ax+Bu\) 且 \(x(t_0)=x_0\),$tt_0 , t_0 $时,所描述的线性定常系统的零状态响应为:
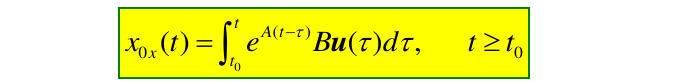
例子:

3.4. 系统总的运动响应

4. 连续时间线性时不变系统的状态转移矩阵
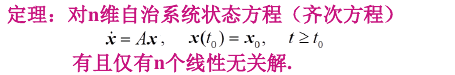
4.1. 基本解阵

4.1.1. 基本解阵的一种形式
对于方程\(\dot{x}=Ax+Bu,~~ x(t_0)=x_0 ,~~ t\geq t_0\),,一个可能的基本解阵的形式如下:

4.2. 状态转移矩阵
对于给定的线性定常系统
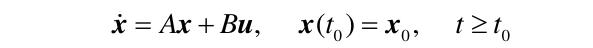
写出矩阵微分方程:

状态转移矩阵即为上面这个矩阵微分方程的\(n\times n\)解阵
即状态转移矩阵是\(\Phi(t-t_0)\)
- 状态转移矩阵\(\Phi(t-t_0)\) 与\(t_0\)到\(t\)的时间间隔相关,与具体时刻大小无关
- 状态转移矩阵\(\Phi(0)=I\),说明在初始\(t_0\)时刻,没有任何的状态转移
4.2.1. 状态转移矩阵和基本解阵的关系()
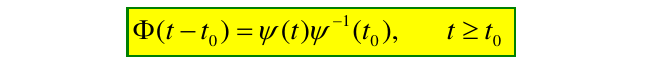
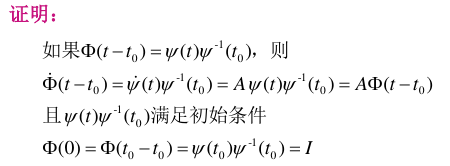
4.2.2. 状态转移矩阵的形式
对于线性定常系统来说,它的状态转移矩阵就是矩阵指数函数,即

需要注意的是\(\Phi(t-t_0)\)是唯一确定的,尽管基础解阵\(\Psi\)不是唯一的,即:

4.2.3. 状态转移矩阵用于零输入、零响应、全响应
根据上面状态转移矩阵的形式的讨论,可以得到状态转移矩阵用于零输入、零响应、全响应的关系
对于线性定常系统:
\[ \dot{x}=Ax+Bu,~~~x(t_0)=x_0,~~~t\geq t_0 \]
(1)零输入响应
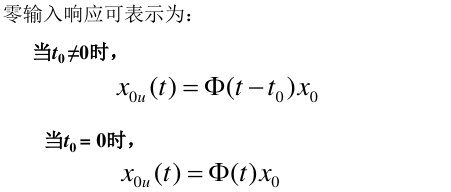
(2)零状态响应

(3)全响应

4.2.4. 求解状态响应

4.2.4.1. 积分法
- 先求出状态转移矩阵\(\Phi(t)=e^{At}\)
- 在利用定义计算
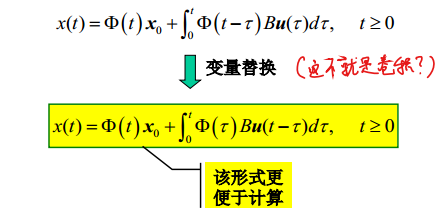
4.2.4.2. 拉氏变换法
- 不需要单独求状态转移矩阵\(\Phi(t)=e^{At}\)
- 一步到位
结果:
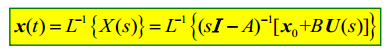
来由:
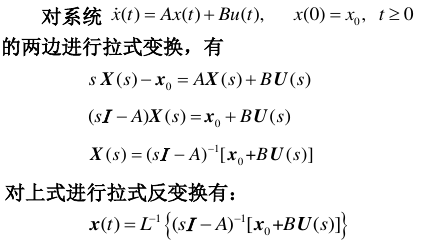
4.2.5. 求解输出响应

4.2.5.1. 例子

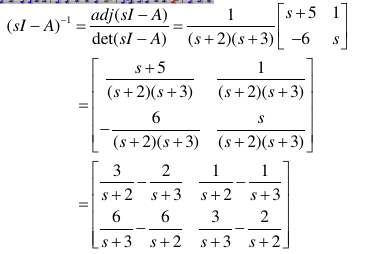
(1)使用积分法先求状态响应\(x(t)\),再求输出响应
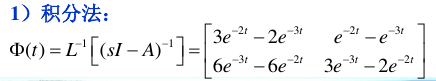

(2)使用拉氏变换法先求状态响应\(x(t)\),再求输出响应

4.2.6. 状态转移矩阵的性质
4.2.6.1. \(\Phi(0)=I\)

4.2.6.2. \(\dot{\Phi}(t)=A\Phi(t)=\Phi(t)A\)
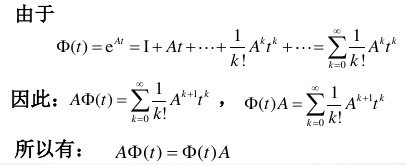
4.2.6.3. \(\Phi(t_1+t_2)=\Phi(t_1)\Phi(t_2)=\Phi(t_2)\Phi(t_1)\)
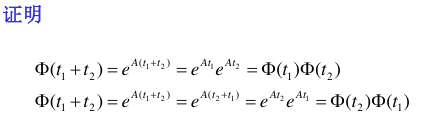
4.2.6.4. \(\Phi^{-1}(t)=\Phi(-t),\Phi^{-1}(-t)=\Phi(t)\)

4.2.6.5. \(\Phi(t_2-t_0)=\Phi(t_2-t_1)\Phi(t_1-t_0)\)
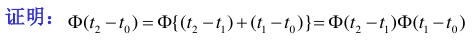
4.2.6.6. \(\Phi(kt)=[\Phi(t)]^{k}\)
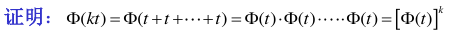
4.2.6.7. \(A=\Phi(0)\)
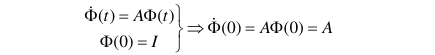
4.2.6.8. 其他
- \(\frac{d}{dt}\Phi(t-t_0)=A\Phi(t-t_0)=\Phi(t-t_0)A\)
- \(\frac{d}{dt}\Phi^{-1}(t-t_0)=-A\Phi(t-t_0)=-\Phi(t-t_0)A\)
5. 连续时间线性时不变系统的脉冲响应矩阵
5.1. 脉冲函数
5.1.1. 脉冲函数的定义
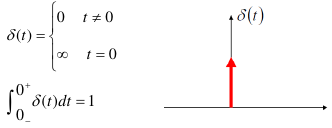
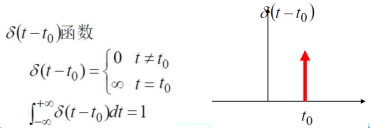
5.1.2. 脉冲函数的性质

5.1.3. 脉冲信号的意义
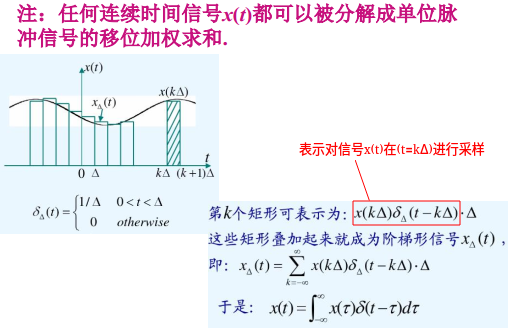
5.2. 脉冲响应矩阵
5.2.1. 单输入单输出系统
对单输入单输出的连续时间线性时不变系统,在初始状态为零的条件下,在任意输入u作用下,系统的输出y(t)可表示为:
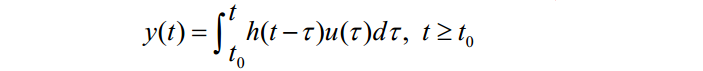
其中,\(h(t-\tau)\)为对应与\(\delta(t-\tau)\)的脉冲响应
也就是信号与系统里面的: 零状态响应=脉冲函数\(\otimes\)输入
5.2.2. 多输入多输出系统

对多输入多输出的连续时间线性时不变系统,在初始状态为零的条件下,在任意输入u作用下,系统的输出y(t)可表示为:

5.3. 脉冲响应矩阵和状态空间描述
对连续时间线性时不变系统:
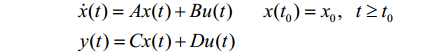
在初始状态为0的条件下,系统脉冲响应矩阵表达式为:
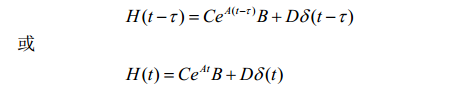
推导如下:

5.3.1. 一些结论


(1)输出零输入响应:
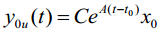
(1)输出零状态响应:
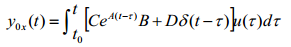
注意与状态的零状态\(x_{0u}\)、零输入响应\(x_{0x}\)的区分
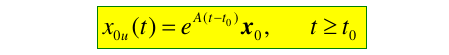
5.4. 脉冲响应矩阵和传递函数矩阵

6. 连续时间线性[时变]系统的状态转移矩阵
6.1. 状态转移矩阵
对于连续时间线性时变系统:
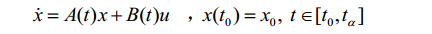
其状态转移矩阵为:

的\(n\times n\)解阵,即\(\Phi(t,t_0)\)
6.2. 基本解阵

6.3. 状态转移矩阵和基本解阵的关系
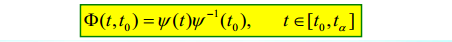
6.4. 状态转移矩阵\(\Phi(t,t_0)\)的形式
对于连续时间线性时变系统:
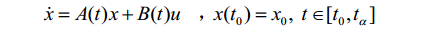
其状态转移矩阵为:
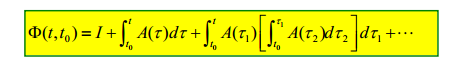

6.5. 状态转移矩阵\(\Phi(t,t_0)\)的性质
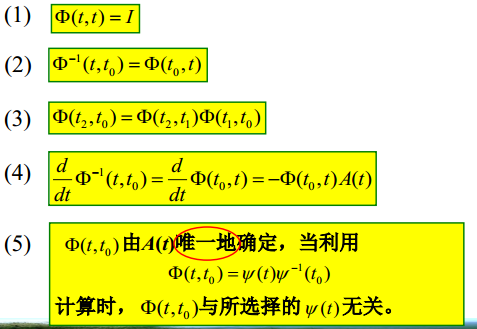
6.6. 连续时间线性[时变]系统的响应
6.6.1. 状态响应
线性时变系统的系统状态方程:
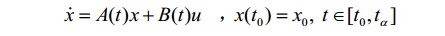
方程的解即为状态响应

6.6.2. 输出响应
线性时变系统的状态空间描述和初始状态为:
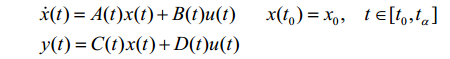
并且有状态响应的表达式:
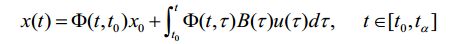
可得系统的输出响应:
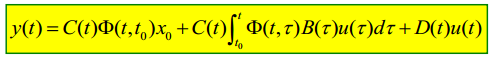
7. 连续时间线性[时变]系统的离散化形式
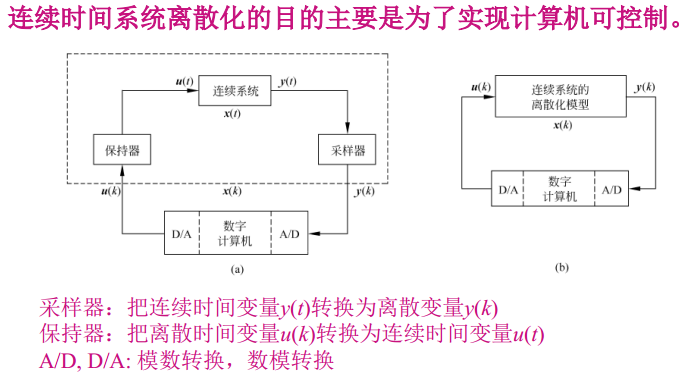
7.1. 采样约定
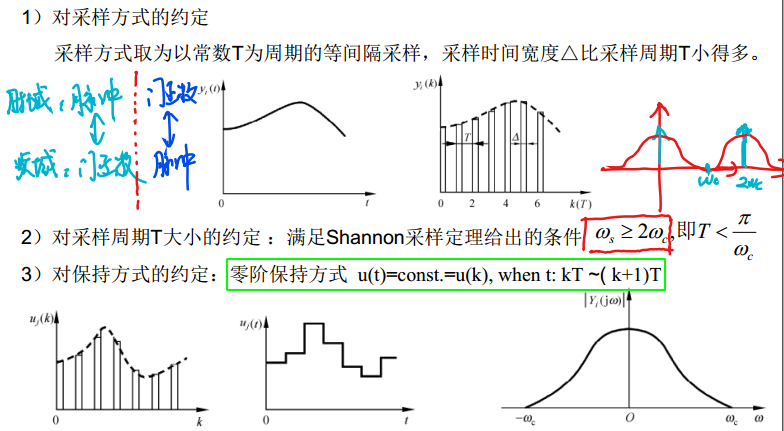
7.2. 基本结论
给定连续时间线性时变系统:
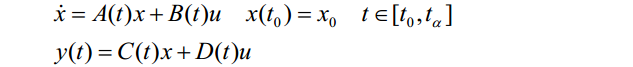
则其在基本约定下的时间离散化描述为:
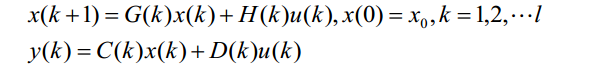
其中,
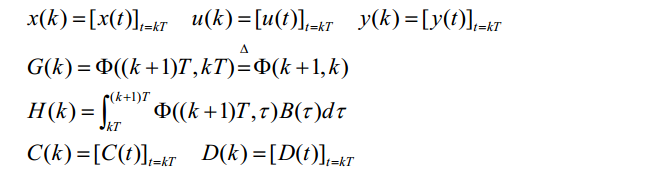
7.3. 状态转移矩阵\(\Phi\)
对离散时间线性时变系统:
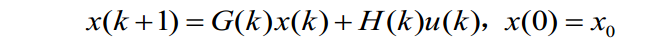

8. 连续时间线性[时不变]系统的离散化形式
对于线性时不变系统,可以看做是时变系统的特例:
\[ \begin{aligned} \dot{x}=Ax+Bu \\ y=Cx+Du \end{aligned} \]
系统矩阵G可以写成如下形式:
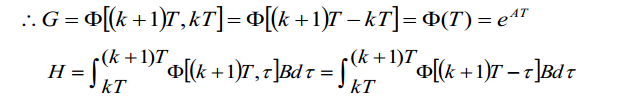

8.1. 例子

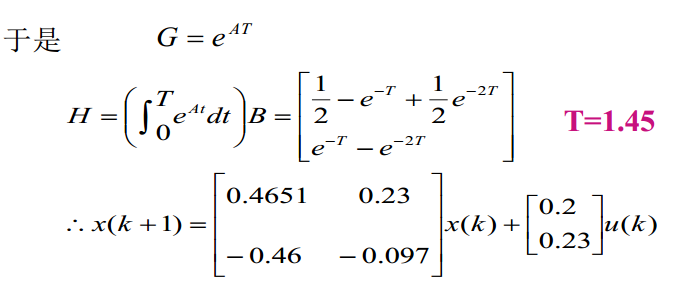
8.2. 状态转移矩阵\(\Phi\)
对离散时间线性时不变系统:
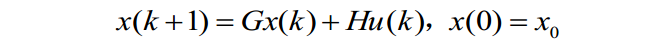
状态转移矩阵\(\Phi\)具有如下形式:
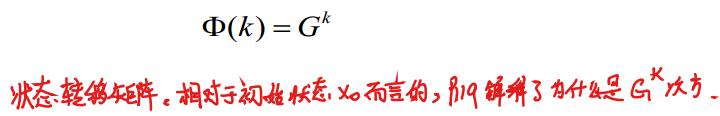
为什么是\(G^{k}\)? 可参见下面的补充内容
"由于时不变系统的系统矩阵G是常数,那么每迭代一次,就对初始状态\(x(0)\)乘一次G,那么最终的状态转移矩阵就是\(G^{k}\)"
补充:
