对随机噪声和干扰的积分处理
我们现在的目的在于为动态系统中随机变量的积分提供合适的方法,当然,我们不能对未知的随机值进行积分,但我们可以对其方差和协方差进行积分,用于对不确定性进行传播。
这对于在连续时间系统(被离散化)中的状态估计器建立协方差矩阵是必须的
考虑一个连续时间系统
\[ \dot{x}=f(x,u,w) \]
其中,
- \(x\)是状态向量
- \(u\)是控制信号,含有噪声\(\tilde{u}\),因此,对控制量的观测\(u_m=u+\tilde{u}\)
- \(w\)是随机干扰的向量
对于噪声和干扰,都被假设为高斯过程,分别有
\[ \tilde{u} \sim \mathcal{N}\{0,U^c\} \]
\[ w^c \sim \mathcal{N} \{0, W^c\} \]
其中,上标 \(^c\)表示连续时间上的不确定性标记,这是我们想要积分的对象
控制信号中的噪声\(\tilde{u}\)和随机干扰\(w\)在性质上有明显差异
- 离散化的时候,控制信号在固定时间\(n\Delta t\)被采样,于是有\(u_{m,n}\triangleq u_m(n\Delta t)=u(n\Delta t)+\tilde{u}(n \Delta t)\),测量部分在积分间隔内被看做是固定的常数,如\(u_m(t)=u_{m,b}\),因此,在采样时间\(n\Delta t\)时刻的噪声也被认为是常数,即
\[ \tilde{u}(t)=\tilde{u}(n\Delta t)=\tilde{u}_n,~~ n\Delta t < t <(n+1) \Delta t \tag{324} \]
- 而扰动项\(w\)不能被采样
结果,在积分时间\(\Delta t\)内,对两种对象的处理方式不一样。
标准形式处理噪声和扰动
连续时间误差状态方程(式322)可以线性化为:
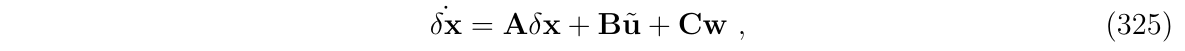
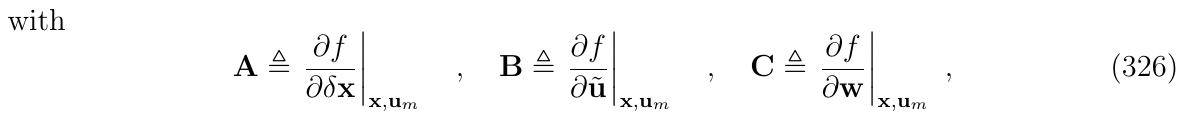
然后在给定采样时间间隔\(\Delta t\)内进行积分,得到离散化形式:
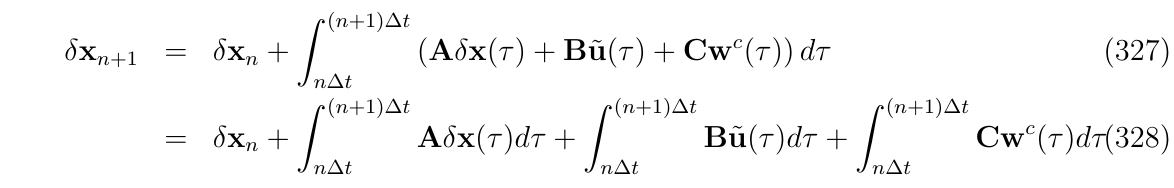
会得到3种非常不一样的形式,如下:
- 状态转移部分: 从附录B,我们知道动态的部分是积分得到的转移矩阵,即:
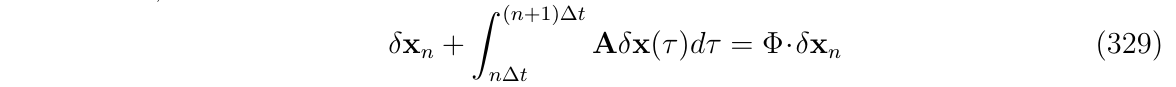
其中,转移矩阵\(\Phi=e^{A\Delta T}\)可以使用闭式表达或者使用不同精确度等级的近似
- 测量噪声部分: 从式(324),可以得到:
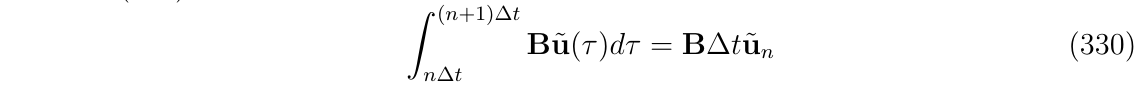
这意味着测量噪声,一旦被采样,就以确定的形式被积分,因为其在积分区间内的behavior是已知的.
- 随机干扰部分: 从概率论,我们知道在时间间隔\(\Delta t\)内对连续时间的高斯白噪声进行积分,将产生离散的高斯脉冲\(w_n\),如下:
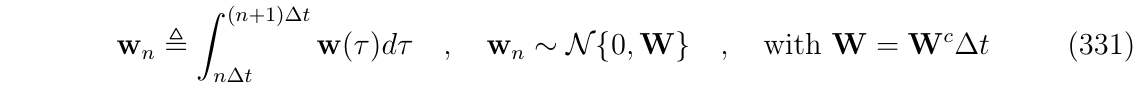
与上面测量噪声部分相反,扰动在积分区间内是不确定的,因此需要随用随机变量来积分。
因此,离散时间下,误差状态方程可以写成:
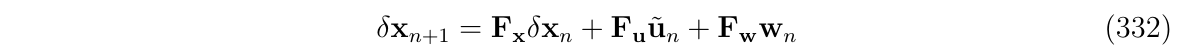
其中,转移矩阵、控制和扰动矩阵如下:
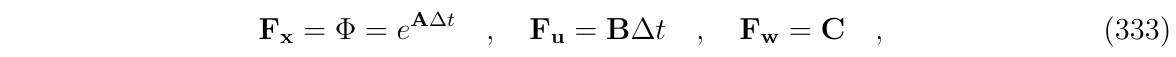
根据噪声和干扰的强度,有:
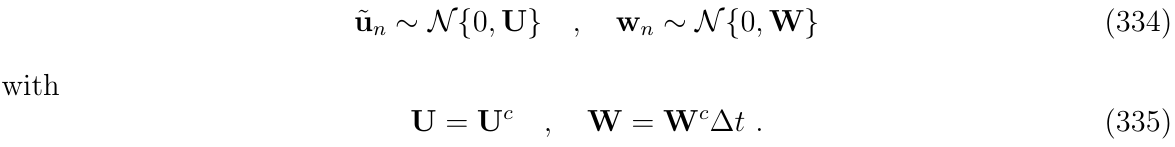
总结
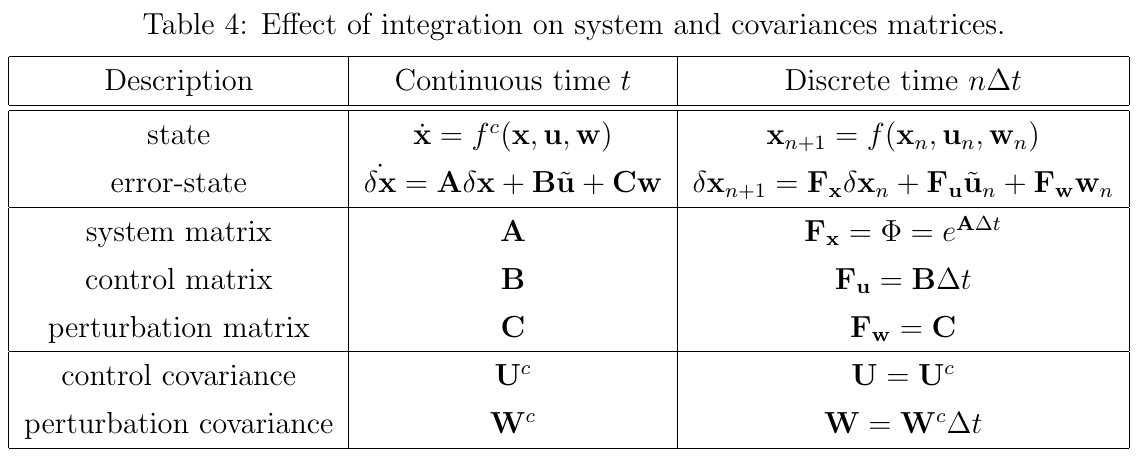
EKF的预测阶段,将会传播误差状态的均值和方差,根据如下方程:
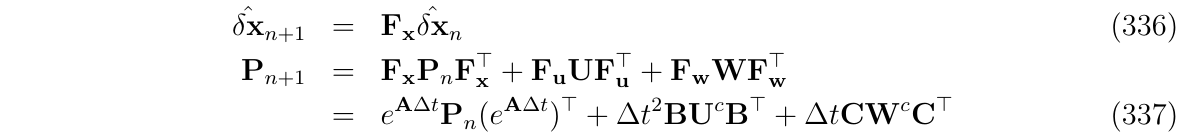
在这里,观察积分区间的不同项是很重要和很有说明意义的:
- 动态误差项是指数函数形式的\(e^{A \Delta t}\)
- 测量噪声项是二次的
- 干扰误差项是线性的(一次)
简化形式处理噪声和扰动脉冲
简化形式
我们经常遇到这样的情况(例如,重用现有代码或解释其他作者的文档时),EKF预测方程的形式比我们这里使用的更简单,即
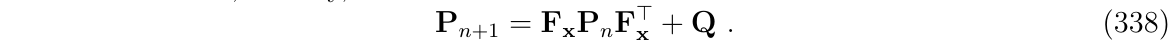
这相当于一般的离散时间动态系统:
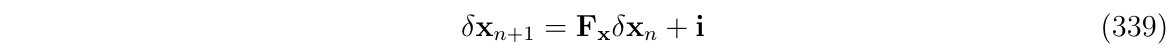
其中,i是服从零均值,方差为Q的高斯分布,是一个随机(白色,高斯)脉冲的向量,将直接添加到\(t_{n+1}\)时刻的状态向量上:
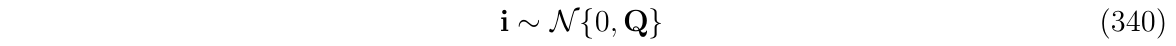
矩阵Q被简化的认为是这个脉冲的协方差矩阵,其计算等式如下: (与式337是一致的)
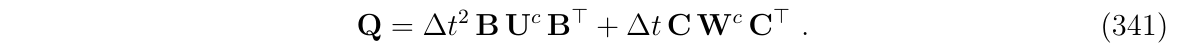
进一步
在脉冲不影响全部状态(full state)的情况下[这是常有的事情],矩阵Q不是完全对角的,可能包含大量的0,于是可以使用下面的等式(添加了一个系数矩阵\(F_i\)而已):
(式339)可以变成:
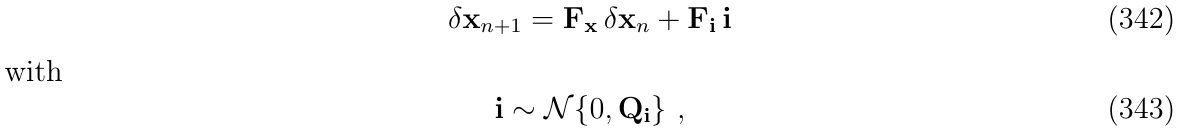
其中,矩阵\(F_i\)简单地将每个单独的脉冲映射到它影响到的状态向量的一部分(简单来说,就是想影响那一个状态,就在对应的对角线维度上设置值)。
这样一来,相关的协方差\(Q_i\)则较小且呈全对角线,因此(式336,337)可以变成:
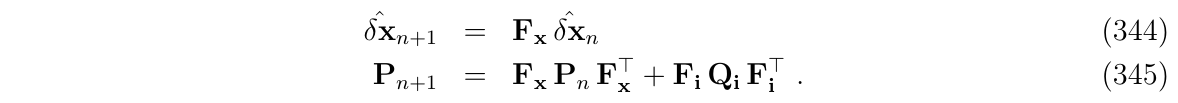
显然,无论是上面的式子,还是(式336,337),都是等价的,因为:
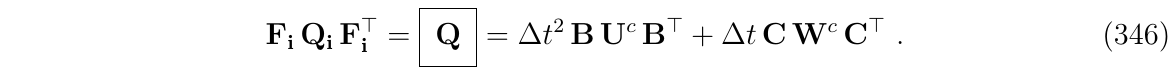
完整版IMU例子
使用标准形式处理噪声和扰动
在前面的四元数的状态误差卡尔曼-Quaternion-kinematics-for-the-error-state-KF,我们研究了IMU的误差状态卡尔曼滤波器的构造,误差状态系统如(式133)所定义,其包含了
nominal statex,error-state\(\delta x\)- 控制信号\(u_m=u+\tilde{u}\)
- 干扰\(w\)
分别如下:
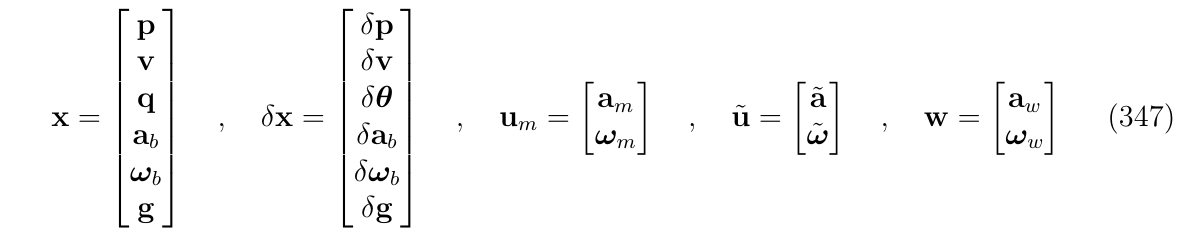
在IMU的模型中,就像我们在本文档中所考虑的那样,控制噪声\(\tilde{u}\)对应于IMU测量中的附加噪声(\(w_n\)),而扰动会影响IMU的偏置(bias),因此导致产生随机游走误差
根据(式325),(式275),(式133) 得到连续时间下误差状态系统的: 系统矩阵A,控制B和扰动C矩阵
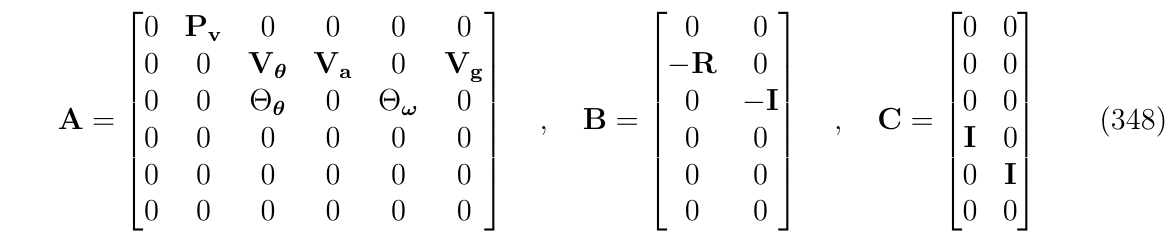
回顾(式325),(式275),(式133):
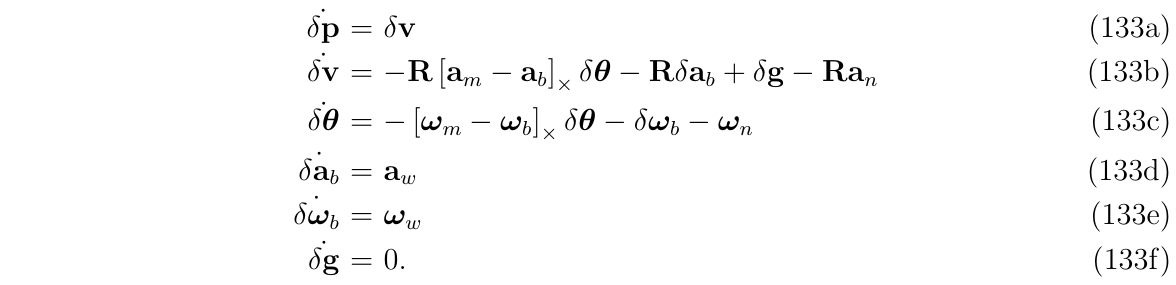
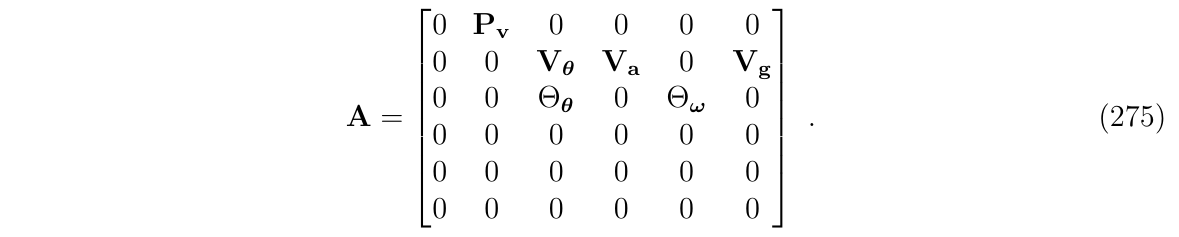
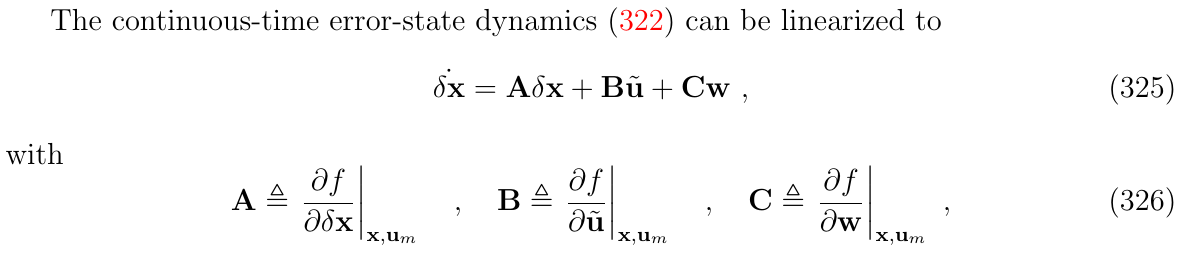
在imu的常规情况下,加速度计和陀螺仪的三个轴是一致的,因此,噪声和干扰是各向同性的(等方性的),他们的标准差(标量)如下:
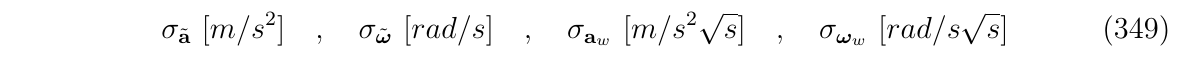
然后他们的协方差是完全对角的,如下:
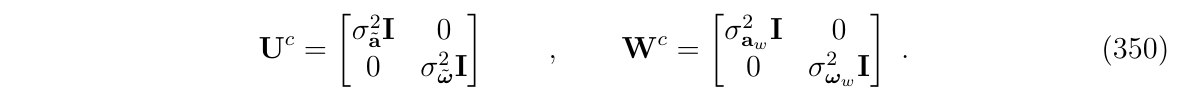
系统以间隔时间\(\Delta t\)的采样,并且按照(式332-335)进行演化====>
即有离散时间下的误差状态系统,离散时间下,误差状态方程可以写成:
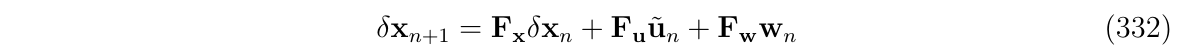
其中,转移矩阵、控制和扰动矩阵如下:
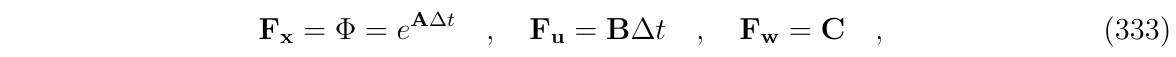
根据噪声和干扰的强度,有:
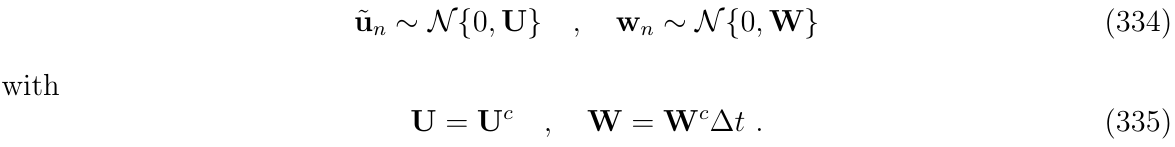
使用简化形式处理噪声和扰动(常见)
使用简化形式,则有误差状态方程:
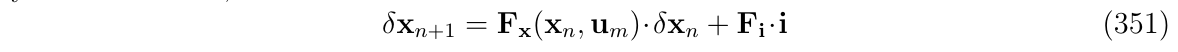

状态转移矩阵\(\Phi\)和扰动矩阵如下:
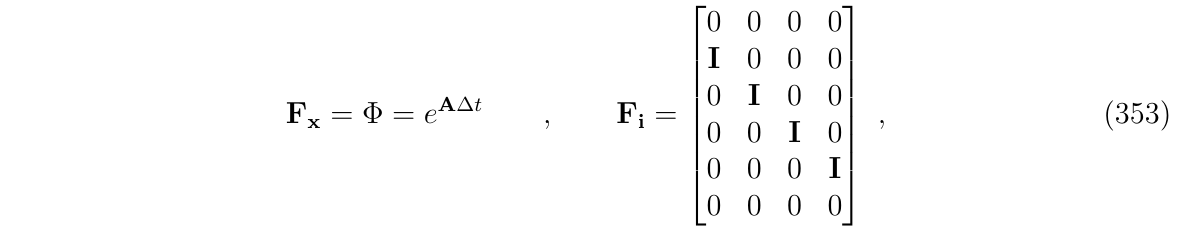
脉冲的方差分别是: