控制相关线性系统理论
Source
Edit
History

第四章-控制系统的李雅普诺夫稳定性分析

Catalogue
  1. 1. 1. 控制系统的李雅普诺夫稳定性分析
    1. 1.1. 1.1. 对自动控制系统的要求
    2. 1.2. 1.2. 两种经典稳定性判据
      1. 1.2.1. 1.2.1. 奈奎斯特稳定判据
      2. 1.2.2. 1.2.2. 劳斯判据
  2. 2. 2. 李雅普诺夫(Lyapunov)稳定性分析方法
    1. 2.1. 2.1. 间接法——第一法
      1. 2.1.1. 2.1.1. 推导
      2. 2.1.2. 2.1.2. 例子
    2. 2.2. 2.2. 直接法——第二法
      1. 2.2.1. 2.2.1. 先导知识——二次型及其定号性
        1. 2.2.1.1. 2.2.1.1. 二次型
        2. 2.2.1.2. 2.2.1.2. 正定二次型
        3. 2.2.1.3. 2.2.1.3. 二次型标量函数
        4. 2.2.1.4. 2.2.1.4. 定号性
        5. 2.2.1.5. 2.2.1.5. Sylvester(塞尔维斯特)准则
        6. 2.2.1.6. 2.2.1.6. 矩阵A正定
      2. 2.2.2. 2.2.2. 一致渐近稳定判定
        1. 2.2.2.1. 2.2.2.1. 大范围内渐近稳定
        2. 2.2.2.2. 2.2.2.2. 李氏函数V(x,t)
        3. 2.2.2.3. 2.2.2.3. 形象描述
      3. 2.2.3. 2.2.3. 渐进稳定判定
      4. 2.2.4. 2.2.4. 一致稳定(等幅震荡)(非渐近稳定)
      5. 2.2.5. 2.2.5. 不稳定
      6. 2.2.6. 2.2.6. 例子1(大范围渐近稳定)
      7. 2.2.7. 2.2.7. 例子2
      8. 2.2.8. 2.2.8. 例子3(一致稳定)(等幅震荡)
      9. 2.2.9. 2.2.9. 例子4(不稳定)
  3. 3. 3. 线性系统的李雅普诺夫稳定性分析
    1. 3.1. 3.1. 线性定常系统(连续)
      1. 3.1.1. 3.1.1. 线性定常系统李氏函数的求法
      2. 3.1.2. 3.1.2. 根据求法得到的推论
      3. 3.1.3. 3.1.3. 例子
    2. 3.2. 3.2. 线性时变系统(连续)
      1. 3.2.1. 3.2.1. 线性时变系统李氏函数的求法
    3. 3.3. 3.3. 线性定常系统(离散)
      1. 3.3.1. 3.3.1. 线性定常(离散)系统李氏函数的求法
      2. 3.3.2. 3.3.2. 例子
    4. 3.4. 3.4. 线性时变系统(离散)
      1. 3.4.1. 3.4.1. 线性时变(离散)系统李氏函数的求法
  4. 4. 4. 问答
    1. 4.1. 4.1. 稳定性的一般定义
      1. 4.1.1. 4.1.1. BIBO稳定
      2. 4.1.2. 4.1.2. 直观感受
    2. 4.2. 4.2. 线性定常系统稳定的充要条件
      1. 4.2.1. 4.2.1. 稳定性判据
        1. 4.2.1.1. 4.2.1.1. 直接解法
        2. 4.2.1.2. 4.2.1.2. 赫尔维茨稳定判据
        3. 4.2.1.3. 4.2.1.3. 劳斯判据
        4. 4.2.1.4. 4.2.1.4. 奈奎斯特(Nyquist)准则
  5. 5. 5. 参考

1. 控制系统的李雅普诺夫稳定性分析

1.1. 对自动控制系统的要求

  • 稳定：系统工作的前提
  • 准确：稳态误差最小或者无差调节
  • 快速：快速、平稳响应

1.2. 两种经典稳定性判据

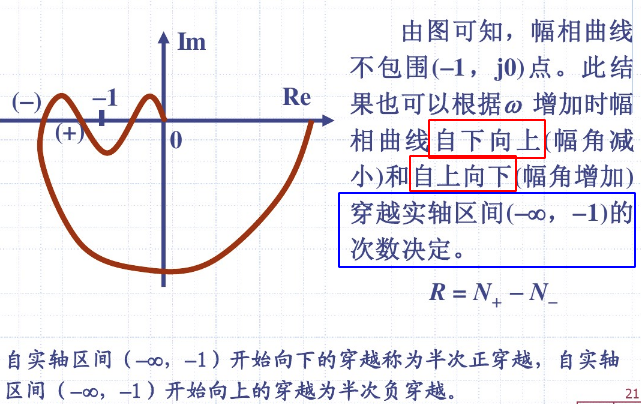
1.2.1. 奈奎斯特稳定判据

1.2.2. 劳斯判据

稳定的条件：系统传递函数的极点全部位于复平面左侧

必要条件：闭环传递函数特征方程的所有系数全部为正（不允许为0或负数）

充要条件：劳斯表的第一列元素全部为正

稳定判据：

2. 李雅普诺夫(Lyapunov)稳定性分析方法

2.1. 间接法——第一法

通过解系统微分方程，利用解的性质判断，特征根全是负实数根

基本处理思路：

  • 将非线性状态方程线性化
  • 解线性化定长系统的特征值========>判定是否稳定

2.1.1. 推导

设有系统\(\dot{x}=f(x,t)\)

其中，

  • R(x)是包含对x的二次以及二次以上的高阶导数项，Ax为线性化之后的一次近似

所以，有 \[ \dot{x}=Ax \] 关于稳定性的判断

  • 如果矩阵A的所有特征值都具有负实部，则\(x_e\)总是渐近稳定的，而且系统的稳定性与高阶导数项R(x)无关
  • 如果矩阵A的特征值中，至少有一个具有正的实部，则无论高阶项R(x)如何，\(x_e\)总是不稳定的
  • 如果矩阵A的特征值中，至少有一个的实部为0，则\(x_e\)具有局部稳定特性，此时原方程不能使用其一次近似\(Ax\)来表征，此时属于临界状况，此时局部稳定性取决于高阶导数项R(x)

2.1.2. 例子

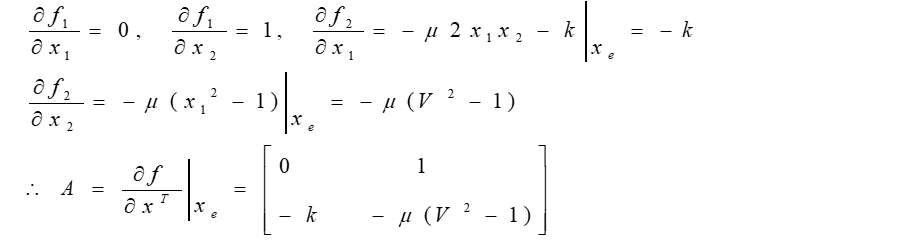
2.2. 直接法——第二法

2.2.1. 先导知识——二次型及其定号性

2.2.1.1. 二次型

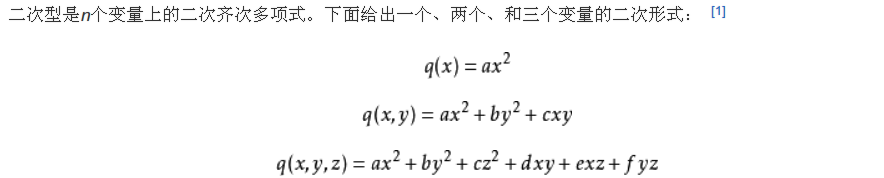
2.2.1.2. 正定二次型

设有如下二次型：

\[ f(x_1,x_2,\cdots,x_n)=X^T A X \]

其中，矩阵A是对称矩阵(\(A=A^T,X=(x_1,x_2,\cdots,x_n)\))

如果

\[ \begin{aligned} \forall x \in R^n, X \neq 0 \end{aligned} \]

都有:

\[ f(x_1,x_2,\cdots,x_n)>0 \]

则称\(f(x_1,x_2,\cdots,x_n)\)是正定二次型，并且矩阵A正定

2.2.1.3. 二次型标量函数

二次型标量函数具有如下形式：

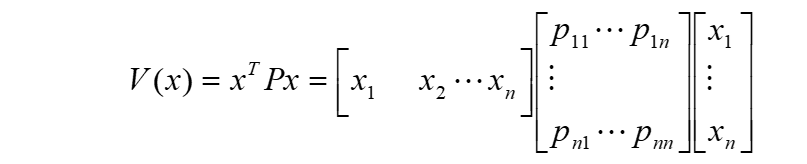
其中，矩阵P为实对称矩阵，即\(p_{ij}=p_{ji}\)

2.2.1.4. 定号性

二次型最基本的特性就是其定号性，即\(V(x)\)在坐标原点附近的特性。

2.2.1.5. Sylvester(塞尔维斯特)准则

二次型函数的正定性可以由S准则来判定，即

2.2.1.6. 矩阵A正定

充要条件

  • 正惯性指数(即正值的特征值个数)等于n
  • 矩阵A与单位矩阵合同
  • 矩阵A的顺序主子式大于0 (见后面补充)
  • 矩阵A的特征值大于0

必要条件

  • 矩阵A的行列式大于0 (但是行列式大于0的矩阵不一定正定)

补充

(1)顺序主子式

取n阶方阵的部分元素化为行列式形式。方阵的第k阶行列式是由该方阵的前k行和k列元素组成

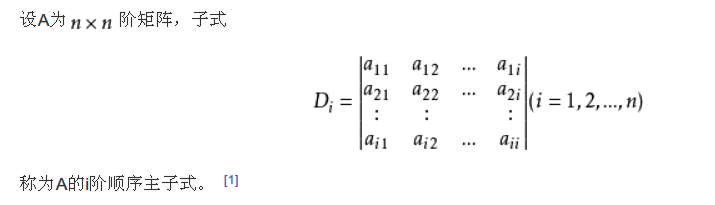
例子:

2.2.2. 一致渐近稳定判定

2.2.2.1. 大范围内渐近稳定

如果当\(||x|| \rightarrow \infin\) 时，有\(V(x,t) \rightarrow \infin\)，则系统在坐标原点的平衡状态是大范围内渐近稳定的。

2.2.2.2. 李氏函数V(x,t)

2.2.2.3. 形象描述

2.2.3. 渐进稳定判定

2.2.4. 一致稳定(等幅震荡)(非渐近稳定)

2.2.5. 不稳定

2.2.6. 例子1(大范围渐近稳定)

2.2.7. 例子2

2.2.8. 例子3(一致稳定)(等幅震荡)

2.2.9. 例子4(不稳定)

3. 线性系统的李雅普诺夫稳定性分析

3.1. 线性定常系统(连续)

设有线性定常系统\(\dot{x}=Ax\)

则有：

  • 假设矩阵A为非奇异矩阵，则系统唯一平衡状态在原点\(x_e=0\)处
  • 如果它在状态空间中的某域内(包括\(x_e=0\))是渐近稳定的，则它一定是大范围渐近稳定的。
  • 对线性系统\(\dot{x}=Ax\)，其李氏函数\(V(x)\)一定可以取为二次型\(x^TPx\)的形式。

3.1.1. 线性定常系统李氏函数的求法

3.1.2. 根据求法得到的推论

推论：如果系统在\(x_e=0\)处是渐近稳定的(即矩阵A为稳定矩阵)，那么李雅普诺夫方程\(A^TP+PA=-Q\)，对于给定的任意一个正定对称矩阵Q，都有唯一解P

3.1.3. 例子

3.2. 线性时变系统(连续)

设有线性时变系统\(\dot{x}=A(t)x(t)\)

3.2.1. 线性时变系统李氏函数的求法

3.3. 线性定常系统(离散)

设有线性定常离散系统:

\[ x(k+1)=Gx(k),~~~ x_e=0 \]

3.3.1. 线性定常(离散)系统李氏函数的求法

3.3.2. 例子

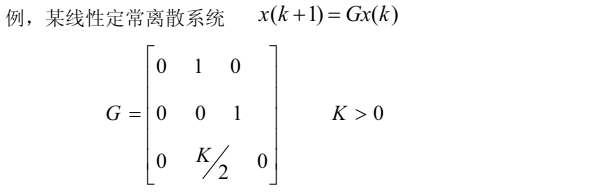
3.4. 线性时变系统(离散)

设有线性时变离散系统:

\[ x(k+1)=G(k+1,k)x(k) ,~~~~ x_e=0 \]

3.4.1. 线性时变(离散)系统李氏函数的求法

4. 问答

4.1. 稳定性的一般定义

4.1.1. BIBO稳定

对与经典的传递函数描述的系统，一般我们讲的稳定指的是BIBO稳定，即有界输入有界输出稳定。

4.1.2. 直观感受

4.2. 线性定常系统稳定的充要条件

4.2.1. 稳定性判据

4.2.1.1. 直接解法

4.2.1.2. 赫尔维茨稳定判据

4.2.1.3. 劳斯判据

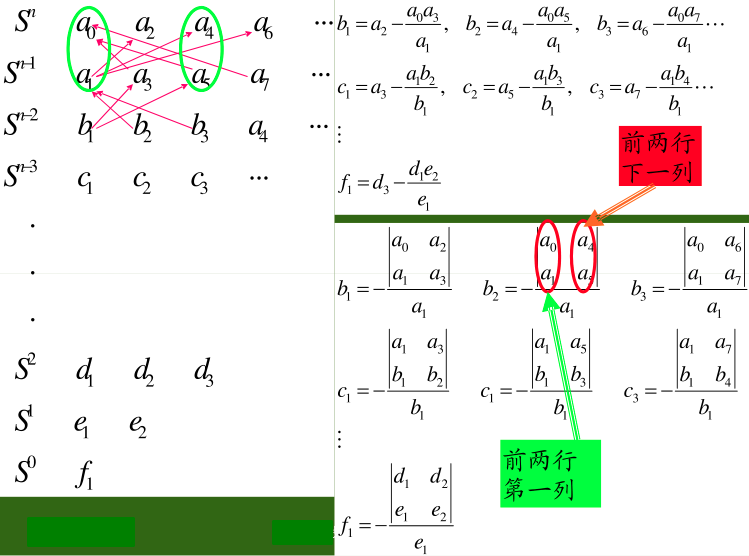
特殊情况:

  1. 某一行第一项为0

  1. 劳斯表出现全零行

4.2.1.4. 奈奎斯特(Nyquist)准则

5. 参考

自动控制原理

系统稳定性

奈氏判据