1. 滑窗优化


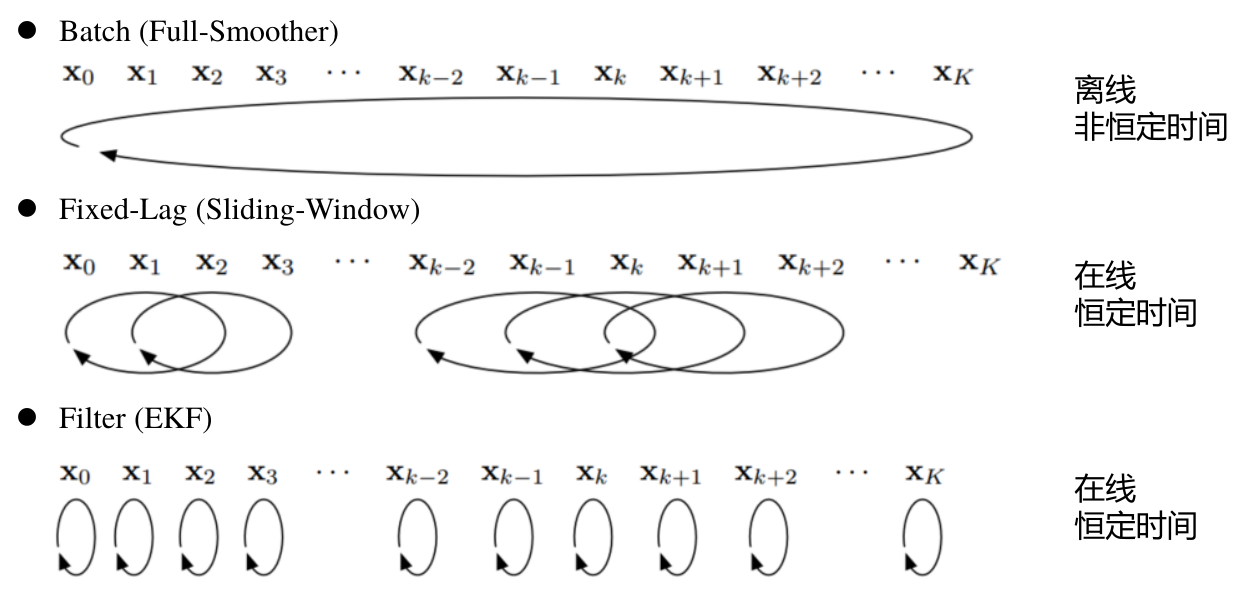
1.1. 一些状态估计方法
1.2. 高斯牛顿收敛性问题

- 可以看到,高斯牛顿方法在高次近似项中,缺了一些项,如在2阶项中缺了一项\(S(x^{*})\)

1.3. 滑窗优化中的雅克比


- 这里对光度参数求导(是相对的光度参数\(e^{a_{ji}},b_{ji}\)),后面会有操作,将这个变成绝对的光度参数导数?
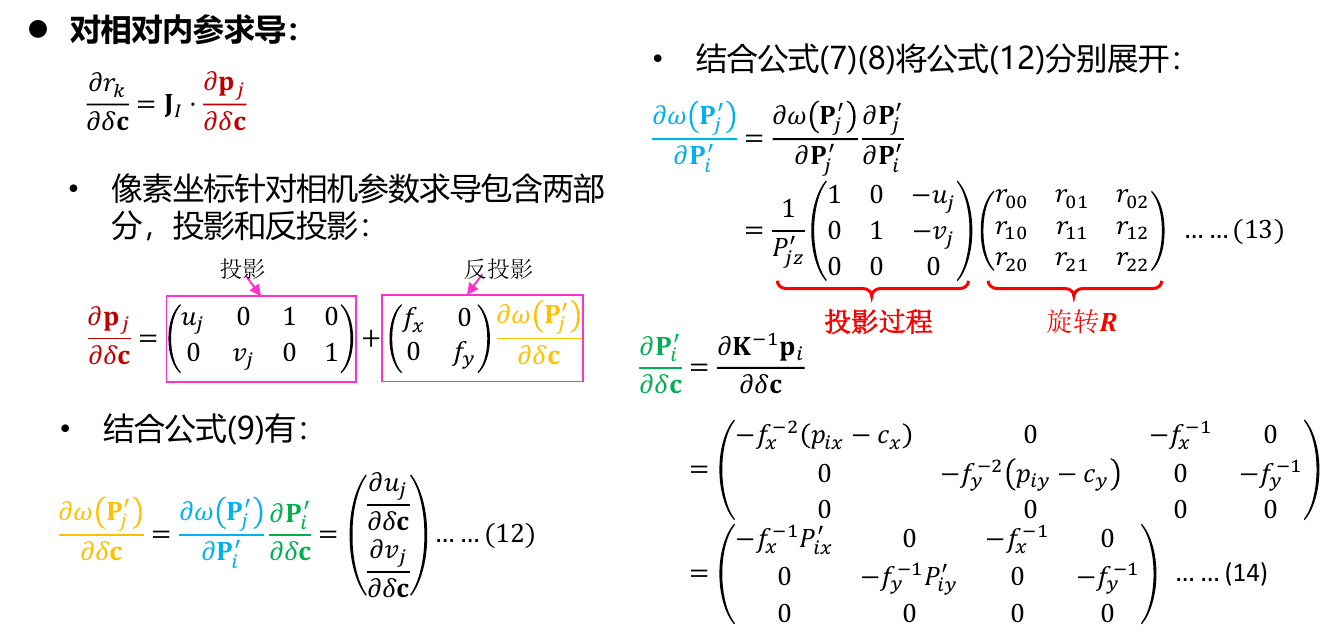
- \(p_j\)是投影点在target帧的像素坐标(\(p_j=x_j\))
- 需要注意的是,虽然相机模型写成了函数的形式,但是实际上是相机内参矩阵K乘以归一化平面点的一个过程
- 因此,
像素坐标对相机内参K的偏导是对\(KP_j'\)进行求导,即\(\frac{\partial x_j}{\partial \delta c}=\frac{\partial KP_j'}{\partial \delta c}=\dot{K}P_j'+K\dot{P_j'}\) - 另外,PPT中的\(u_j,v_j\)是归一化平面坐标,不是像素坐标值(扯)
- \(P_j'\)是投影点在target帧相机坐标系归一化平面上的点
其中,像素坐标对相机内参K的偏导推导过程如下
(1)下面是关于\(part_1 \Longrightarrow \dot{K}P_j'\)这一部分
\[ \begin{aligned} \dot{K}P_j'&=\frac{\partial K}{\partial \delta c}P_j' \\ &=\begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} P_j'[0] \\ P_j'[1] \\ 1 \end{bmatrix} \end{aligned} \]
上面的\((P_j'[0],P_j'[1],1)\)是投影点在target帧的相机坐标系归一化平面上的坐标
需要写成求导的形式
\[ \begin{aligned} \frac{\partial part_1}{\partial \delta c}= J_{part1} \begin{bmatrix} \delta fx \\ \delta fy \\ \delta cx \\ \delta cy \end{bmatrix} \end{aligned} \]
\[ \begin{aligned} \dot{K}P_j' \triangleq \begin{bmatrix} P_j'[0] & 0 & 1 & 0\\ 0 & P_j'[1] & 0 & 1 \end{bmatrix} \end{aligned} \]
(2)下面是关于\(part_2 \Longrightarrow K\dot{P_j'}\)这一部分
主要先关注\(\dot{P_j'}\)
\[ \begin{aligned} \dot{P_j'}= \frac{\partial P_j'}{\partial \delta c}= \underbrace{ \frac{\partial P_j'}{\partial P_j} \frac{\partial P_j}{\partial P_i} \frac{\partial P_i}{\partial P_i'}}_{part_{21}} \underbrace{ \frac{\partial P_i'}{\partial \delta c}}_{part_{22}} \end{aligned} \]
\[ \begin{aligned} & x_j=KP_j' \\ & P_j'=\frac{P_j}{P_j[2]} \\ & P_j=R_{ji}P_i'+t\cdot d_{pi} \\ & P_i'= K^{-1} x_i = \begin{bmatrix} \frac{1}{f_x} & 0 & -\frac{c_x}{f_x} \\ 0 & \frac{1}{fy} & -\frac{c_y}{f_y} \\ 0 & 0 & 1 \end{bmatrix} x_i = \begin{bmatrix} \frac{x_i[0]-c_x}{f_x} \\ \frac{x_i[1]-cy}{f_y} \\ 1 \end{bmatrix} \end{aligned} \]
再次强调
- \(p_j=x_j\)是投影点在target图像上的像素坐标
- \(P_j\)是投影点在target帧相机坐标系的坐标
- \(P_j'\)是投影点在target帧相机坐标系的归一化平面坐标
- \(P_i'\)是点在参考帧的相机坐标系归一化平面坐标
- \(x_i\)是点在参考帧图像上的像素坐标(即相当于ppt中的\(p_i\)(小写))
现在处理\(part_{21}\)
\[ \begin{aligned} part_{21}&= \frac{\partial P_j'}{\partial P_j} \frac{\partial P_j}{\partial P_i} \frac{\partial P_i}{\partial P_i'} \\ &= \frac{\partial P_j'}{\partial P_j} \frac{\partial P_j}{\partial P_i'} \end{aligned} \]
其中,
\[ \begin{aligned} \frac{\partial P_j'}{\partial P_j} &= \frac { \partial \begin{bmatrix} P_j[0]/P_j[2] \\ P_j[1]/P_j[2] \\ 1 \end{bmatrix} } { \partial P_j } \\ &= \begin{bmatrix} \frac{\partial P_j[0]/P_j[2]} { \partial \begin{bmatrix} P_j[0] & P_j[1] & P_j[2] \end{bmatrix} } \\ \frac{\partial P_j[1]/P_j[2]} { \partial \begin{bmatrix} P_j[0] & P_j[1] & P_j[2] \end{bmatrix} } \\ \frac{\partial 1} { \partial \begin{bmatrix} P_j[0] & P_j[1] & P_j[2] \end{bmatrix} } \end{bmatrix} = \begin{bmatrix} \frac{\partial \frac{P_j[0]}{P_j[2]}}{\partial P_j[0]} & \frac{\partial \frac{P_j[0]}{P_j[2]}}{\partial P_j[1]} & \frac{\partial \frac{P_j[0]}{P_j[2]}}{\partial P_j[2]} \\ \frac{\partial \frac{P_j[1]}{P_j[2]}}{\partial P_j[0]} & \frac{\partial \frac{P_j[1]}{P_j[2]}}{\partial P_j[1]} & \frac{\partial \frac{P_j[1]}{P_j[2]}}{\partial P_j[2]} \\ 0 & 0 & 0 \end{bmatrix} \\ &= \begin{bmatrix} \frac{1}{P_j[2]} & 0 & -\frac{P_j[0]}{P_j[2]^2} \\ 0 & \frac{1}{P_j[2]} & -\frac{P_j[1]}{P_j[2]^2} \\ 0 & 0 & 0 \end{bmatrix} \\ &= \frac{1}{P_j[2]} \begin{bmatrix} 1 & 0 & -\frac{P_j[0]}{P_j[2]} \\ 0 & 1 & -\frac{P_j[1]}{P_j[2]} \\ 0 & 0 & 0 \end{bmatrix} \end{aligned} \]
\[ \frac{\partial P_j}{\partial P_i'}=R_{ji} \]
接下来处理\(part_{22}\)
\[ \begin{aligned} part_{22} &= \frac{\partial P_i'}{\partial \delta_c} = \frac {\partial \begin{bmatrix} P_i'[0] & P_i'[1] & 1 \end{bmatrix}^T} {\partial \delta c} \\ &=\frac{\partial K^{-1}x_i }{\partial \delta c} = \frac {\partial \begin{bmatrix} \frac{x_i[0]-c_x}{f_x} \\ \frac{x_i[1]-cy}{f_y} \\ 1 \end{bmatrix}} { \partial \delta c } \\ &= \begin{bmatrix} -\frac{x_i[0]-c_x}{f_x^2} & 0 & -\frac{1}{f_x} & 0 \\ 0 & -\frac{x_i[1]-c_y}{f_y^2} & 0 & -\frac{1}{f_y} \\ 0 & 0 & 0 & 0 \end{bmatrix} \\ &= \begin{bmatrix} -\frac{P_i'[0]}{f_x} & 0 & -\frac{1}{f_x} & 0 \\ 0 & -\frac{P_i'[1]}{f_y} & 0 & -\frac{1}{f_y} \\ 0 & 0 & 0 & 0 \end{bmatrix} \end{aligned} \]
对\(\dot{P_j'}\)的两个子部分进行结合
\[ \begin{aligned} \dot{P_j'}&= \frac{\partial P_j'}{\partial \delta c}= \underbrace{ \frac{\partial P_j'}{\partial P_j} \frac{\partial P_j}{\partial P_i} \frac{\partial P_i}{\partial P_i'}}_{part_{21}} \underbrace{ \frac{\partial P_i'}{\partial x_i} \frac{\partial x_i}{\partial K} \frac{\partial K}{\partial \delta c}}_{part_{22}} \\ &= \frac{1}{P_j[2]} \begin{bmatrix} 1 & 0 & -\frac{P_j[0]}{P_j[2]} \\ 0 & 1 & -\frac{P_j[1]}{P_j[2]} \\ 0 & 0 & 0 \end{bmatrix}R_{ji} \begin{bmatrix} -\frac{P_i'[0]}{f_x} & 0 & -\frac{1}{f_x} & 0 \\ 0 & -\frac{P_i'[1]}{f_y} & 0 & -\frac{1}{f_y} \\ 0 & 0 & 0 & 0 \end{bmatrix} \end{aligned} \]
即可得到如下:
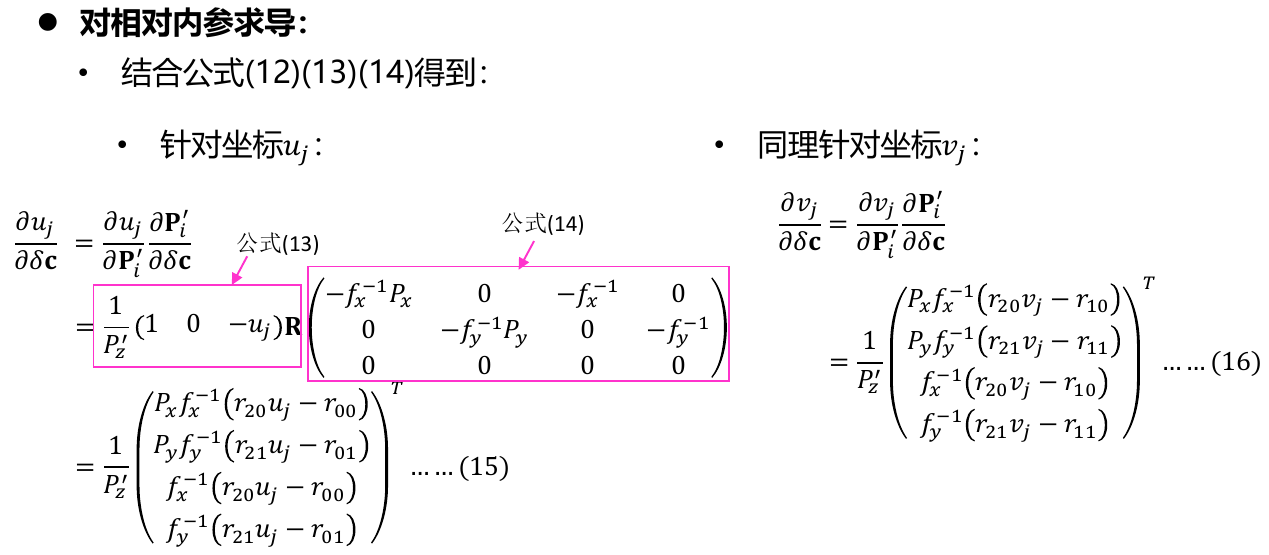
结合part1和part2两部分,最终得到对内参的总体导数:
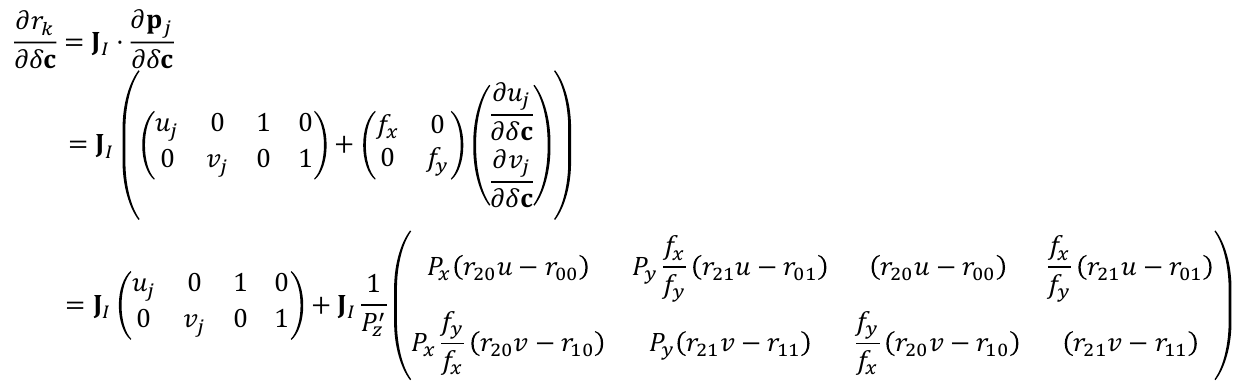
1.4. 伴随性质(From 14讲)
1.4.1. SO3伴随
\[ R \exp(\phi^\wedge)R^T= \exp ((R\phi)^\wedge) \]
1.4.2. SE3伴随
\[ T \exp(\xi^\wedge)T^{-1}=\exp([Ad(T)\xi]^\wedge) \]
其中,伴随Ad(T)形式如下:
\[ \begin{aligned} Ad(T)= \begin{bmatrix} R & t^\wedge R \\ 0 & R \end{bmatrix} \end{aligned} \]
1.5. 零空间
1.5.1. 零空间的定义
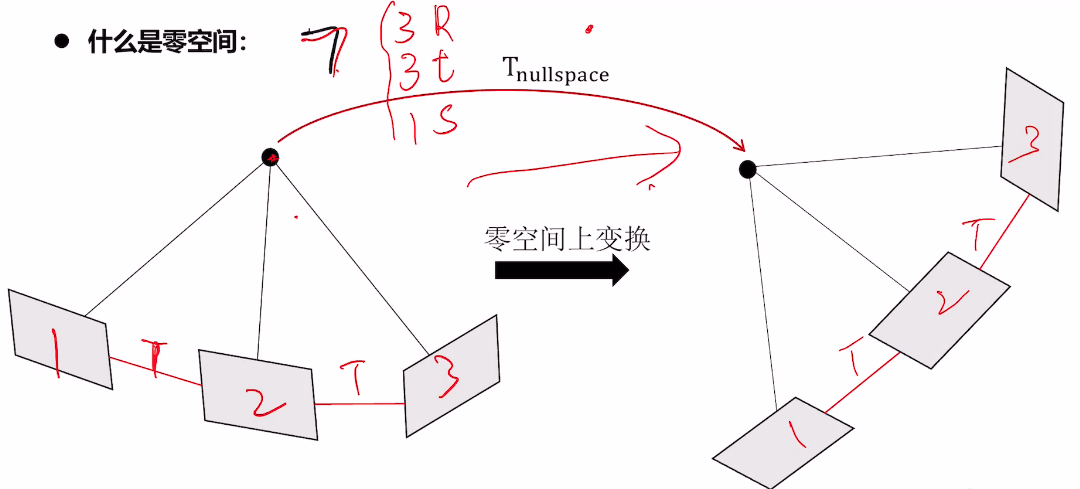
单目 7个自由度不可观
- 旋转量
- 平移量
- 尺度
可观的理解: 不同视角观测某个状态,状态都一样,则是可观的,如GPS得到的绝对位置

1.5.2. 如何求零空间

上面描述了如何将一个global的扰动转换到local(相机坐标系)的扰动,即
\[ \delta \xi_c = Ad_{T_{cw}} \delta \xi_w \]
这样,就可以得到零空间上在每一个local(相机坐标系)的扰动

1.5.3. 零空间的处理



上面的意思是,我们通过增量方程\(H\Delta x=b\)求解出来的增量\(\Delta x=\Delta x_{true}+\Delta x_{nullspace}\),其中零空间增量\(\Delta x_{nullspace}\)满足\(H \Delta x_{nullspace}=0\)
为了求解出真正的增量,需要在求解出来的\(\Delta x\)中减去关于零空间的漂移部分
- 上图中的向量\(v\)就相当于我们求解出来的\(\Delta x\)
- 利用零空间的一组基向量,就可以把这个向量\(v\)投影到零空间上,得到零空间部分\(\Delta x_{nullspace}\)
- 那么再对两个向量相减,得到垂直部分,垂直部分就是我们想要的真正的增量\(\Delta x_{true}=\vec{v}-\vec{v}_{in P_M}=\Delta x-\Delta x_{nullspace}\)
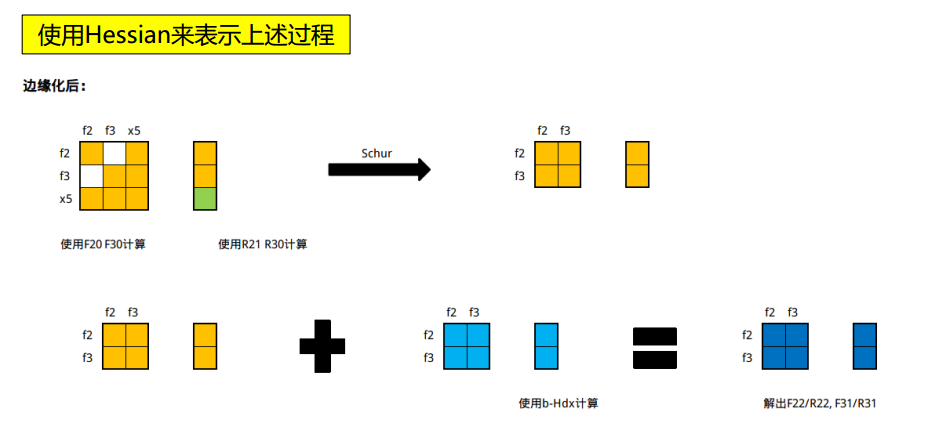
1.6. DSO中的边缘化
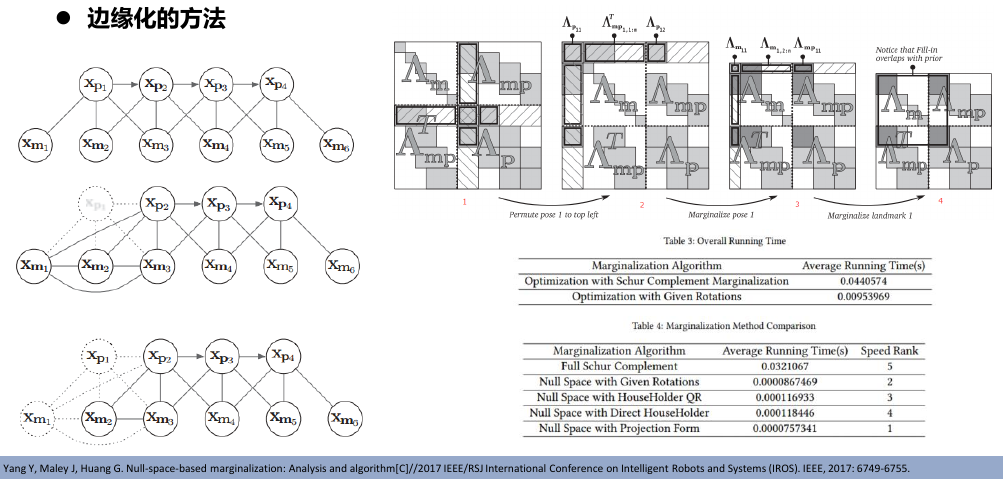
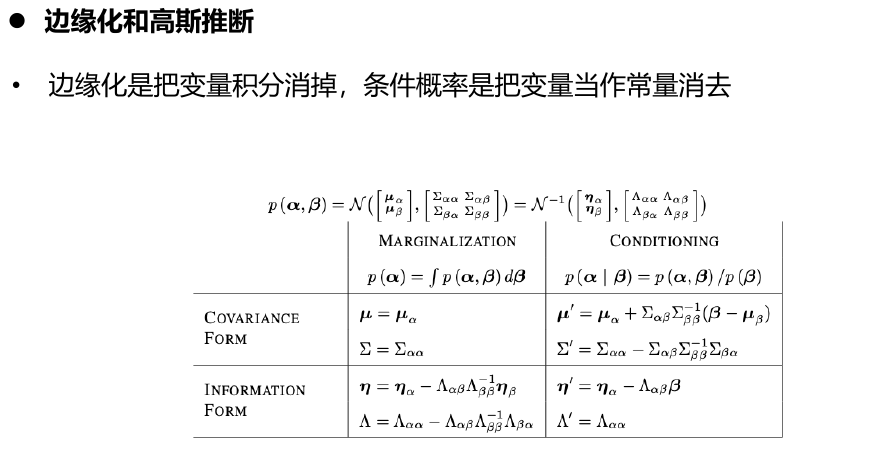
1.6.1. 点——边缘化
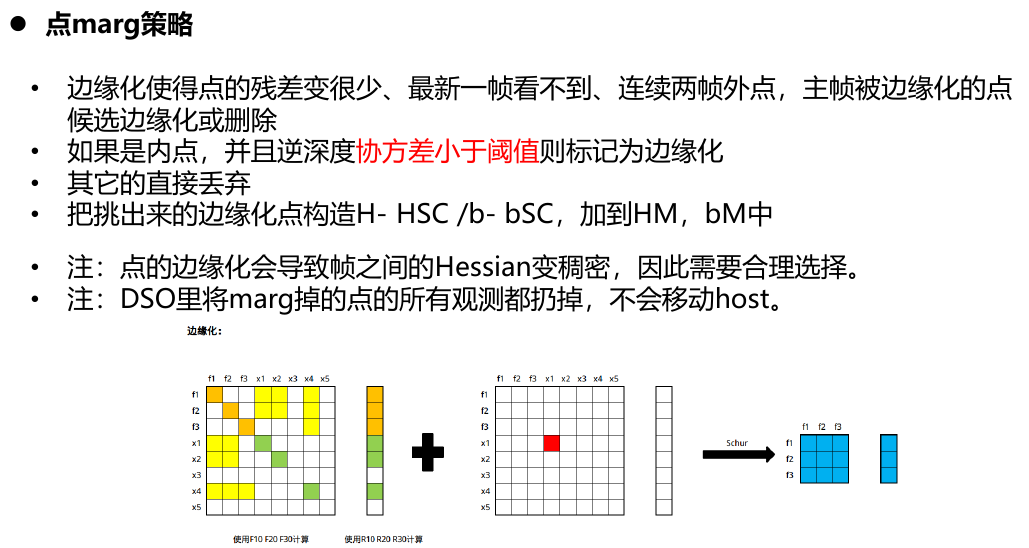
- 对路标点进行marg之后,会在左上角的相机位姿参数块中进行FIll-IN
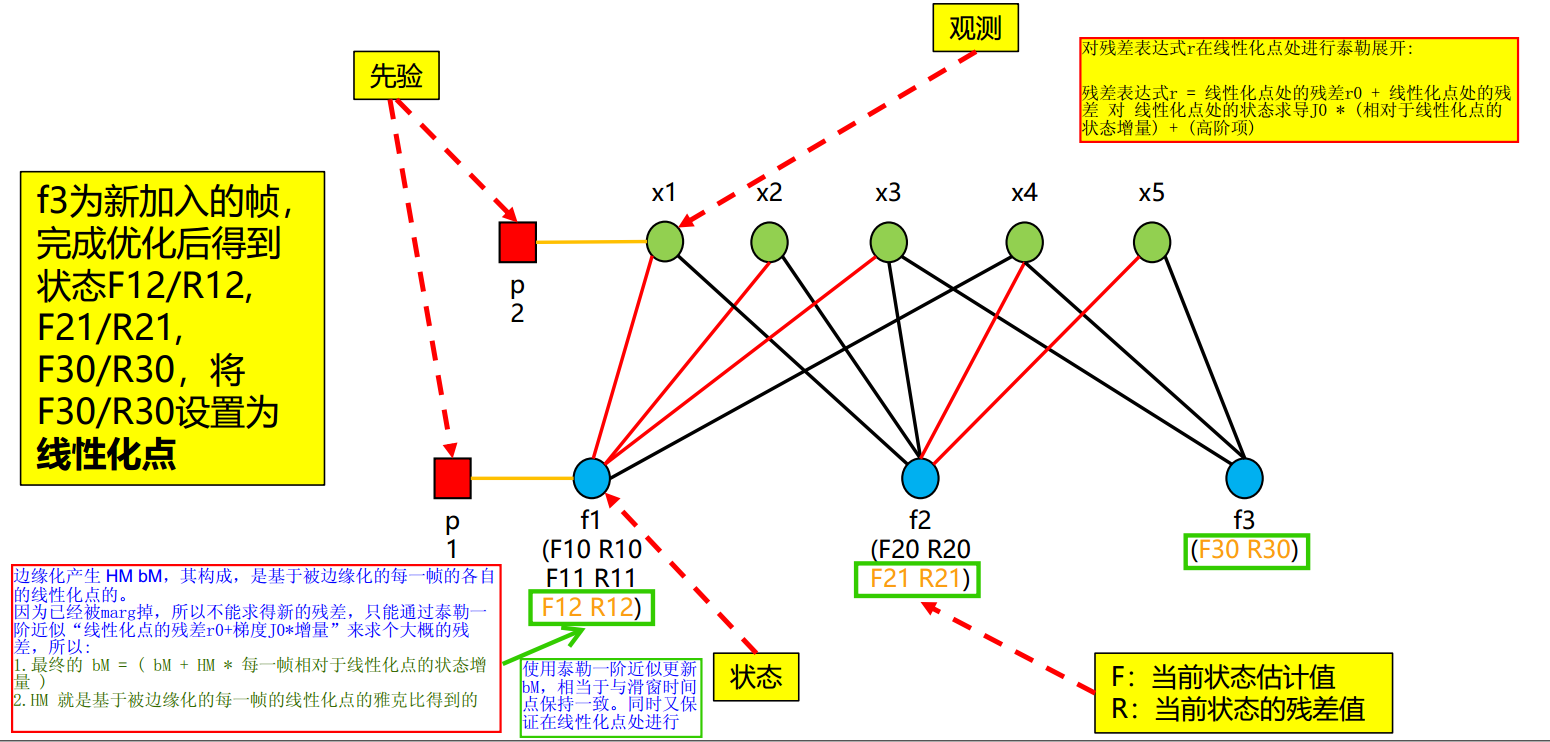
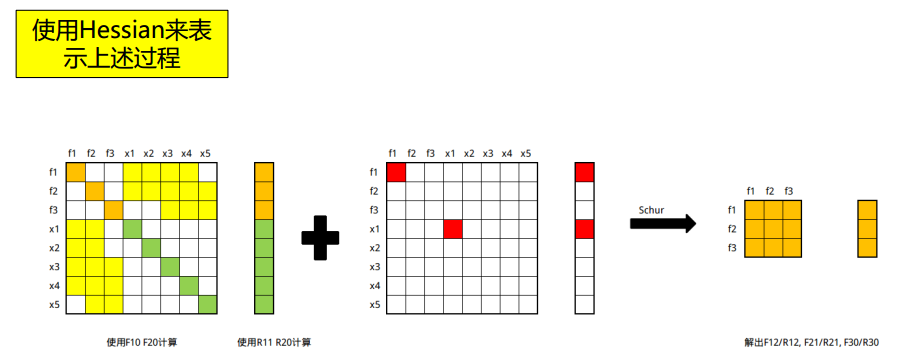
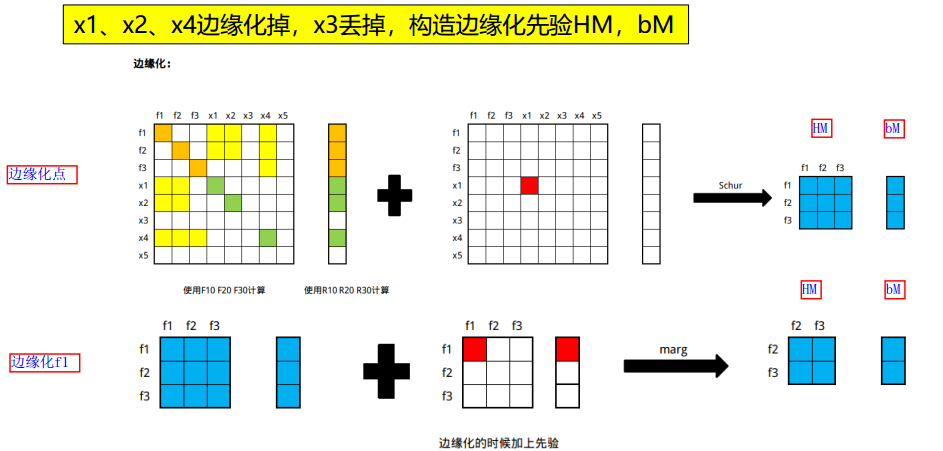
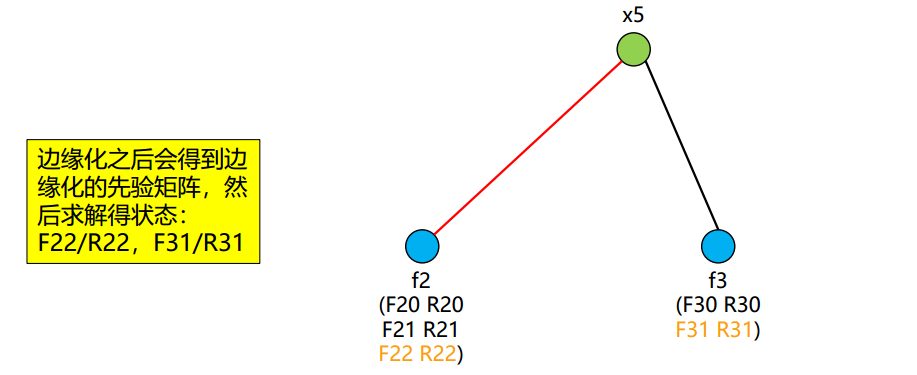
1.6.2. 帧——边缘化
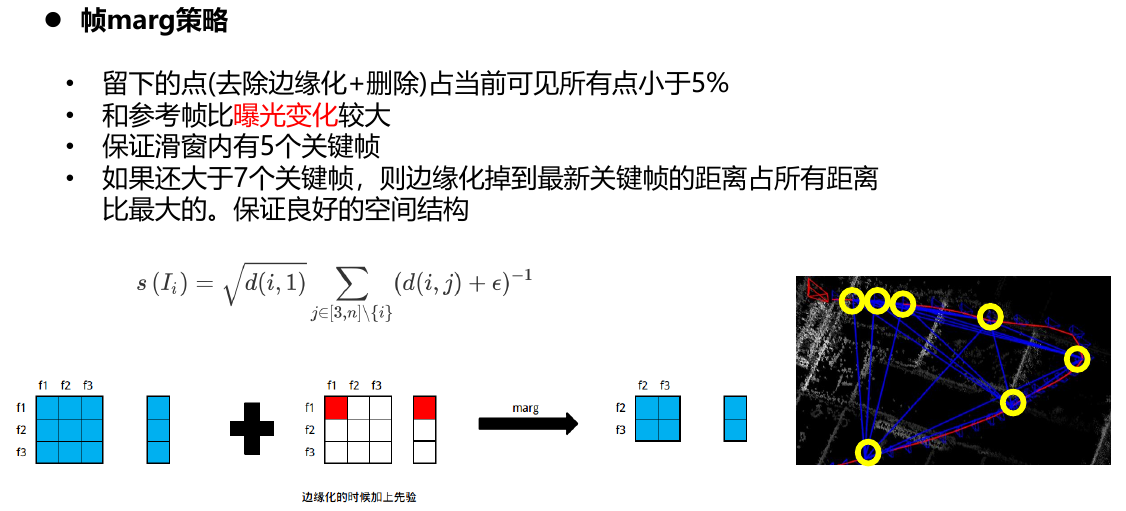
1.6.3. SSE加速
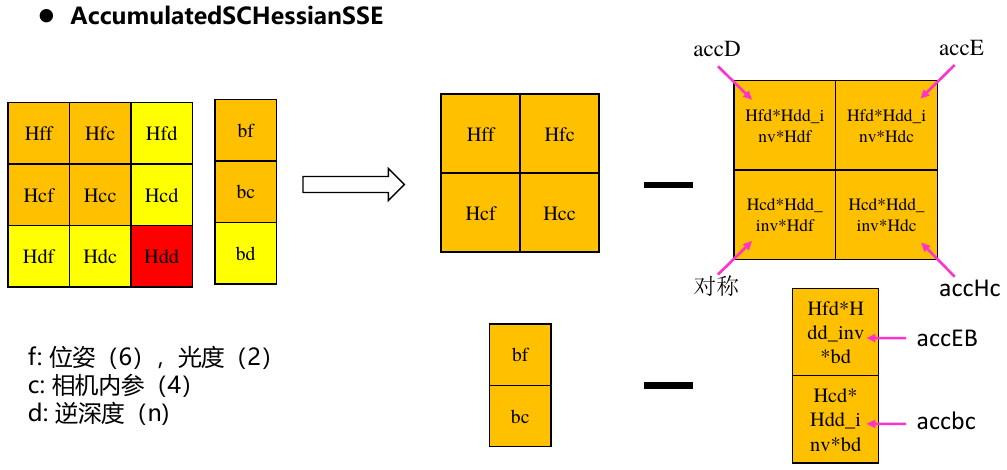
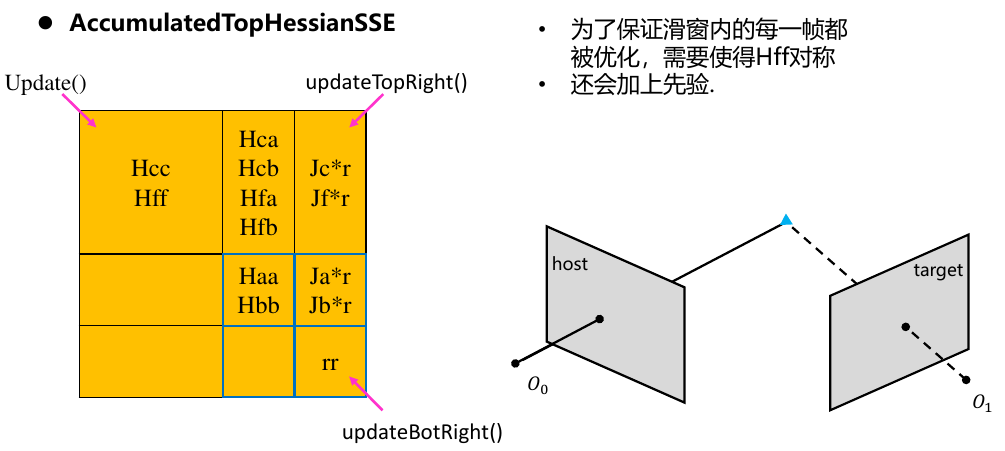
1.7. FEJ
滑动窗口边缘化会带来一些问题,其中一种解决方法是使用FEJ


1.7.1. 举例
滑动窗口边缘化会带来问题
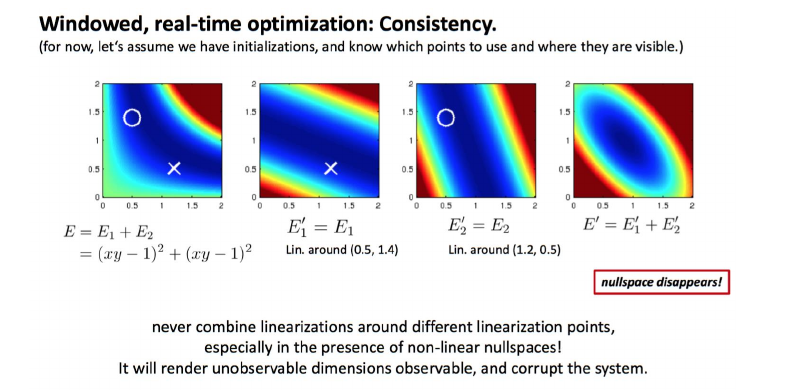
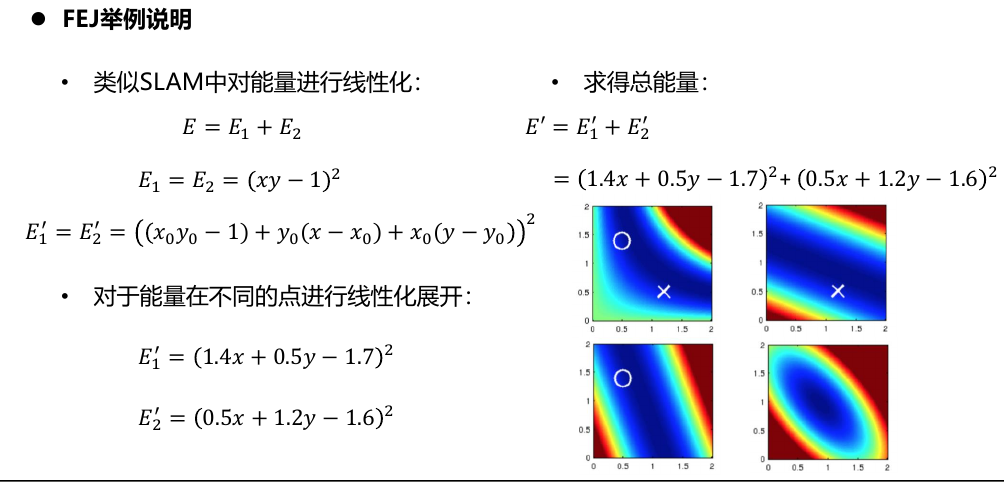
假设有能量函数 \[ E=E_1+E_2 \]
\[ E_1=E_2=(xy-1)^2 \]
根据泰勒公式:
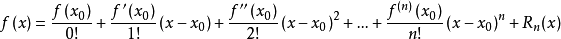
对能量函数进行线性化,即分别对E1和E2进行线性化,即对\((xy-1)\)进行泰勒一阶展开,有:
\[ (xy-1)'=(x_0y_0-1)+y_0(x-x_0)+x_0(y-y_0) \]
那么E1和E2的线性化为:
\[ E_1'=E_2'=[(xy-1)']^2=[(x_0y_0-1)+y_0(x-x_0)+x_0(y-y_0)]^2 \]
取两个状态\(X_0=(0.5,1.4)\)和\(X_1=(1.2,0.5)\),将这两个状态分别代入E1'和E2',即相当于在这两个点处进行线性化,
\[ \begin{aligned} E_1'=(1.4x+0.5y-1.7)^2 \\ E_2'=(0.5x+1.2y-1.6)^2 \end{aligned} \]
然后叠加,最终得到使用两个线性化点之后的能量函数\(E_{X_0X_1}\)
\[ \begin{aligned} E_{X_0X_1} &=E_1'+E_2' \\ &=(1.4x+0.5y-1.7)^2+(0.5x+1.2y-1.6)^2 \end{aligned} \]
对于这样一个使用两个线性化点之后的能量函数,其可行解从一条(xy-1)的双曲线变成了一个椭圆区域,这就是滑动窗口边缘化带来的问题,使得原有的零空间减小了
1.8. DSO的其他trick
1.8.1. 利用伴随
利用伴随性质得到基于线性化点处滑窗内的相对位姿与绝对位姿的关系


1.8.2. 一些说明

1.8.3. 一些solver

1.9. DSO的后端流程
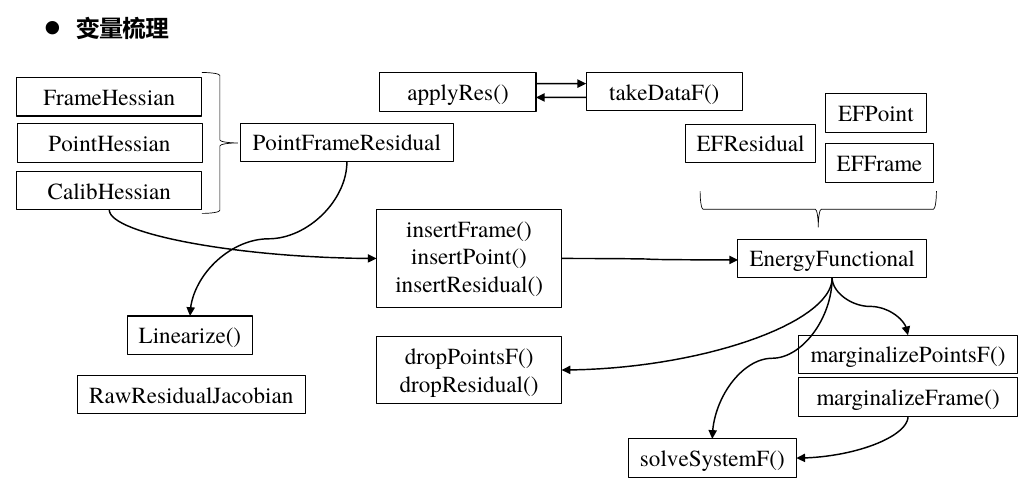
1.10. FEJ+边缘化的一些例子