1. 向量空间
向量空间又称线性空间,是线性代数的中心内容和基本概念之一。
1.1. 向量张成的空间
如果几个向量的线性组合在某一个向量空间中,并且该向量空间仅包括这几个向量的线性组合,那么这个向量空间就叫做这几个向量张成的空间。简单地说,N个向量张成的空间就是N个向量的线性组合
2. 子空间
设V是\(R^n\)的一个非空子集,若V中的任意N个向量的线性组合依然属于V,则称V是\(R^n\)的一个线性子空间,简称子空间。
根据概念,如果V是\(R^n\)的线性子空间,则V一定满足三个条件
- 包含0向量
- 若x是V中的一个向量,那么x与一个变量的乘积\(nx\)也在线性子空间V中——数乘封闭性
- 若a,b是V中的两个向量,那么a+b也在线性子空间V中——加法封闭性
例子: 下面的V是否是\(R^2\)的子空间?
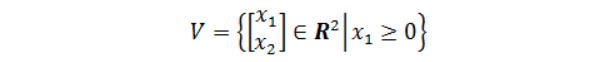
可以通过分量的取值范围得知,V是直角坐标系的一、四象限:
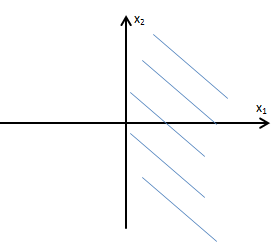
- 由于a1+a2 ≥ 0,所以满足加法封闭性。
- 检验数乘封闭性: 当标量为负数时,得到的结果\(-x\),超越了第一、四象限,不在这个子空间V中,不满足数乘封闭性
- 因此,V不是\(R^2\)的子空间
3. 零空间
A是\(m\times n\)矩阵,x是列向量,如果存在向量集合N,满足
\[ N=\{x \in R^n | Ax =0 \} \]
则称N是矩阵A的零空间
3.1. 零空间与"Ax=0"
可知,零空间是方程Ax = 0的所有解的集合,也就是说,零空间就是方程Ax=0的解向量所张成的空间
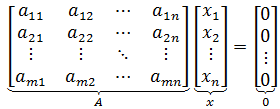
检验零空间是否是\(R^n\)的子空间,即检验
- 加法封闭性
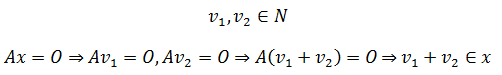
满足
- 数乘封闭性
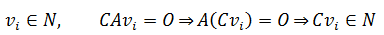
满足
所以零空间也是\(R^n\)的子空间
3.2. 找出零空间
就是解\(Ax=0\),得到解向量,所张成的空间呗
3.2.1. 例子1
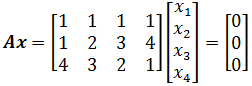
只需求解方程组就可以了,方法之一是将A化为行最简阶梯矩阵:
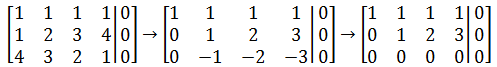
为了求解方便,我们的目标是让方程组的未知数尽量少,所以还可以进一步化简,让台角上方全为0:
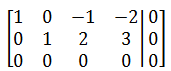
将行最简阶梯矩阵转换为方程组
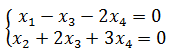
两个方程,四个未知数,那么解向量的个数为\(n-r(A)=4-2=2\),该零空间是由两个向量张成的空间:
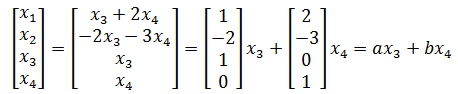
x3,x4可以是任意实数,a,b是线性无关的,所以A的零空间就是a和b张成的空间
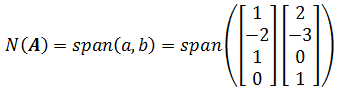
3.2.2. 例子2

3.3. 零空间与线性无关
3.3.1. 线性相关与线性无关

3.3.2. 线性无关矩阵的零空间只包含零向量
\(A_{m\times n}\)由n个列向量组成,那么Ax即表示了对n个列向量的线性组合,即:
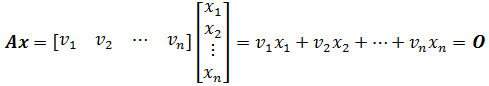
如果A是线性无关的,意味着方程组只有一个全零解,或者说,这个方程的解集是A的零空间,并且这个零空间只包含零向量,即上面列向量的系数(状态)\(\{x_1,x_2,x_3\cdots\}\)全为0
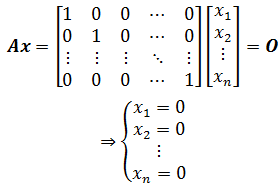
结果:
- 当A是满秩方阵或列满秩的长方矩阵时,A的零空间只有零向量(仅仅是行满秩时就不一定了)
- 当一个矩阵的零空间只有零向量时,说明该矩阵的列向量线性无关
4. 列空间
如果A是\(m\times n\)的矩阵,那么A的列空间是A中所有列向量张成的空间。A的列空间用C(A)表示

4.1. 列空间与"Ax=b"
如果有方程:
\[ Ax=b \]
- 如果b在矩阵A的列空间中(即b可以使用Ax来表示(x不全为0)),此时Ax = b有解
- b不在A的列空间中,Ax = b无解