1. First Estimates Jacobian (FEJ)-EKF

2. 标准EKF-SLAM
(引用崔老师的论文阅读配图)
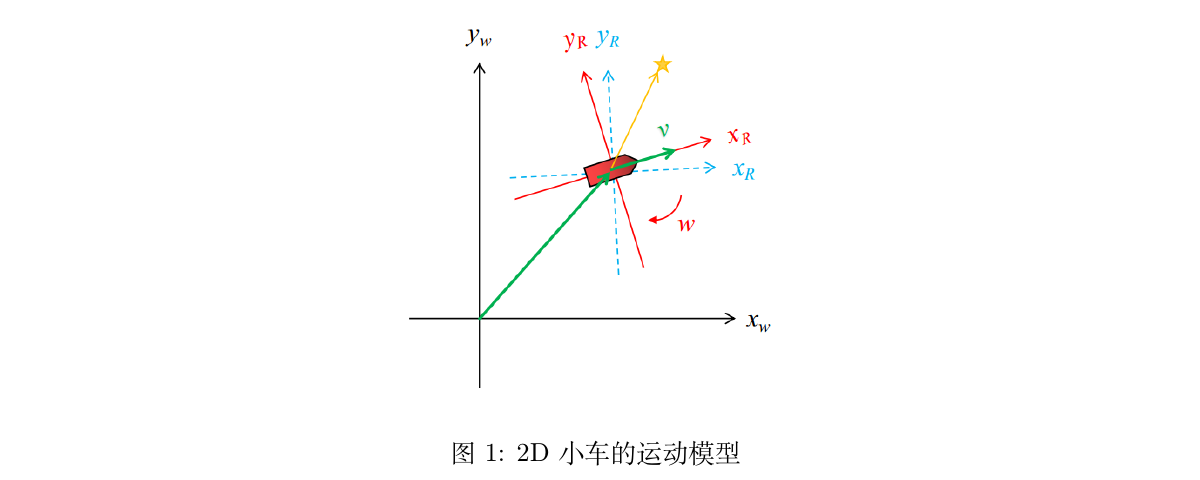
如图所示,是以 2D 平面上的小车为例,且假设运动输入\(u\)为始终沿车头方向的速度\(v\),和角速度\(\omega\),世界坐标系为W(orld),小车坐标系为R(obot)
取状态向量,由小车的位姿以及路标点的在全局坐标系的位置组成
在时间步k,状态向量如下:
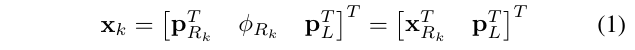
其中,\(x_{Rk}=[p_{Rk}^T,\phi_{Rk}]^T\),表示了小车的位姿(位置和旋转),\(p_L\)则是路标的坐标(世界坐标系)
2.1. EKF传播
在这一步中,得到两个连续时间步之间的姿态变化估计值,然后利用EKF来传播机器人状态估计。
另一方面,由于路标是静态的,它的估计值不会随着新的里程测量的加入而改变
于是,可以得到EKF传播步骤:
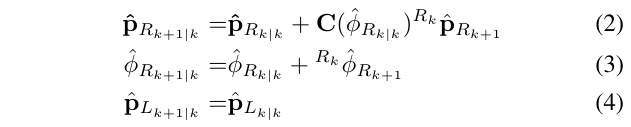
其中,
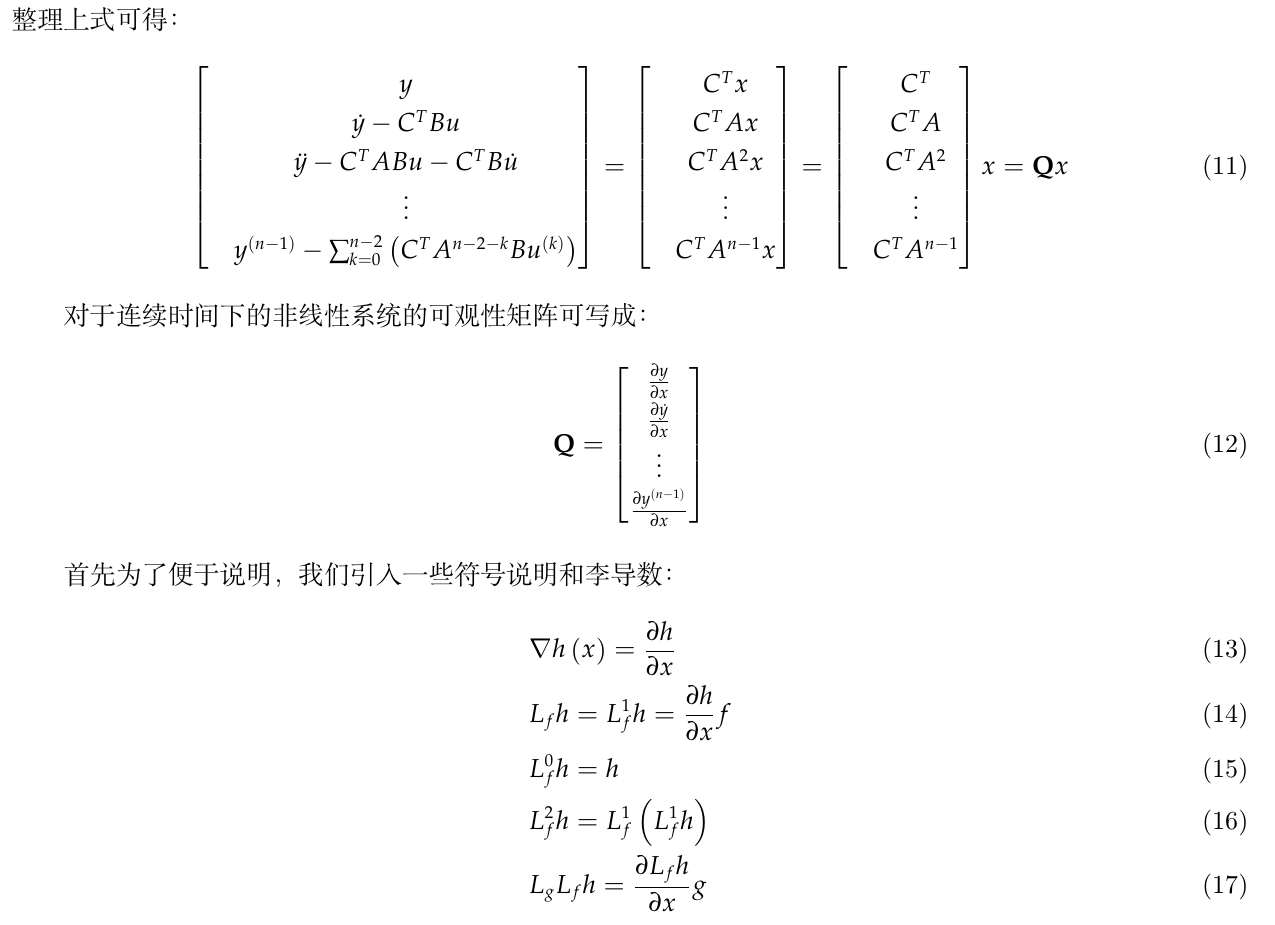
- \(C(\cdot)\)表示了2x2的旋转矩阵(基于k时刻更新之后的从机器人坐标系到世界坐标系的旋转变换)
- \(^{R_k}\hat{x}_{R_{k+1}}=[^{R_k}\hat{p}_{R_{k+1}}^T,^{R_k}\hat{\phi}_{R_{k+1}}]\)是机器人在k到k+1时刻的运动估计,这个估计受到零均值高斯白噪声的影响,白噪声为\(w_k=^{R_k}x_{R_{k+1}}-^{R_k}\hat{x}_{R_{k+1}}\),其协方差矩阵为Q
除了状态传播,线性化的误差状态传播也是需要的,即:
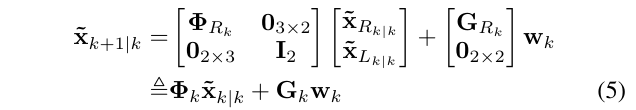
其中,\(\Phi_{R_k}\)是\({3\times 3}\)矩阵,是上面的预测方程对状态量的雅克比,
于是,\(\Phi_{R_k}\)和\(G_{R_k}\)形式如下:
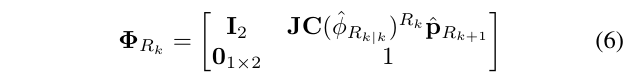
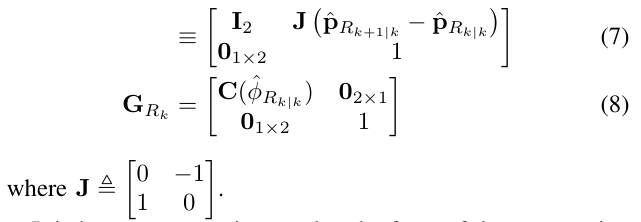
上下标说明 - 下标\(l|j\),是指在时间步长为j的所有测量值处理完毕后,在时间步l处对一个状态量的估计 - \(\hat{x}\)用来表示随机变量x的估计值 - \(\tilde{x}=x-\hat{x}\)表示估计值的与真值的误差 - \(s\phi,c\phi\)分别表示\(\sin \phi\)和\(\cos \phi\)
需要指出的是,上述传播方程的形式是通用的,适用于任何机器人运动学模型(如独轮车、自行车或Ackerman模型).
2.2. EKF更新
EKF中用于更新的观测是路标相对于机器人的相对位置的函数:
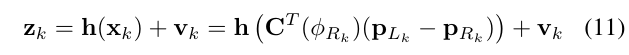
其中,\(v_k\)是协方差为\(R_k\)的零均值高斯测量噪声,在这里,允许观测函数h为任意的2维观测函数,只要它是可逆的(只要我们能从\(z_k\)完全确定机器人相对地标位置的估计值)。
通常,测量函数是非线性的,因此它被线性化,用于EKF,线性化的测量误差方程如下:
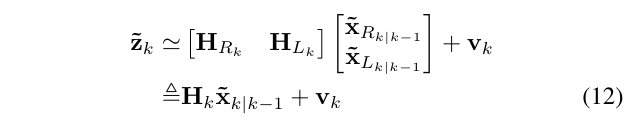
其中,\(H_{Rk}\)和\(H_{Lk}\)是h分别对机器人位姿和路标位置的雅克比,在线性化点\(\hat{x}_{k|k-1}\)处计算得到。使用链式法则,有:
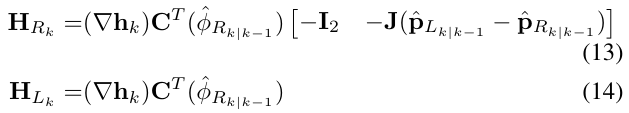
其中,
- \(\bigtriangledown h_k\)表示观测函数h()对于
机器人-路标的相对位置的雅克比 - 如对\(^{R_k}p_L=C^T(\phi_{Rk})(p_L-P_{RK})\)的雅克比,也就是观测函数h()对路标在机器人坐标系的坐标的雅克比
- 线性化点在\(\hat{x}_{k|k-1}\)
3. SLAM的非线性可观测性分析
3.1. 先导内容(引自_崔老师_连续非线性系统的可观性)
3.1.1. 非线性系统的可观测性矩阵
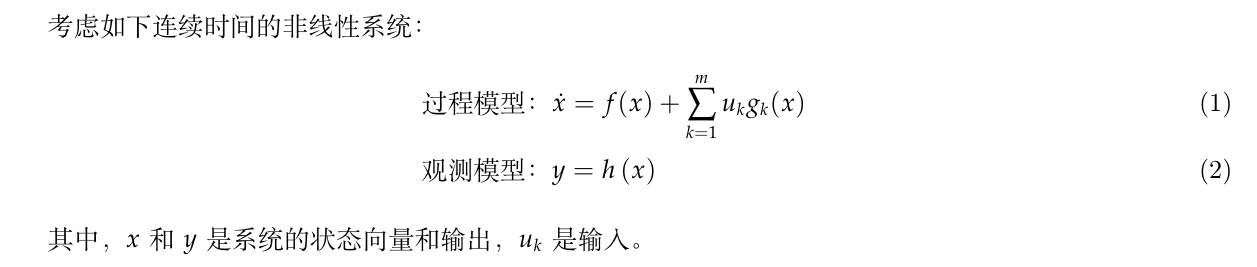


3.2. 基于小车实例的可观测性分析
在研究EKF系统模型的可观测特性之前,先对连续时间非线性SLAM系统进行可观测性分析,将实际非线性系统的性质与EKF系统模型的性质进行比较,我们可以确定标准EKF系统中的一个基本缺点,这将会导致滤波器的不一致性。
下面证明SLAM系统不满足可观测性秩条件,因此它既不是局部弱可观测的,也不是局部可观测的
对于连续时间的分析,我们使用了一个上面所述的2D平面小车运动学模型,以及相对位置测量模型。连续时间下的系统模型为:
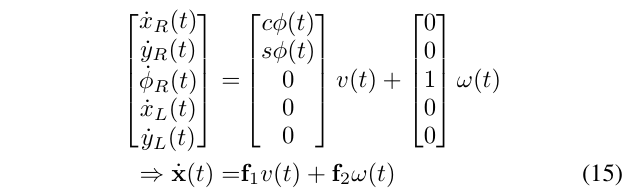
其中,\(u\triangleq [v,w]^T\)是控制输入量,包含线速度和角速度。
连续时间的相对位置测量模型为(即路标点在机器人坐标系的坐标):
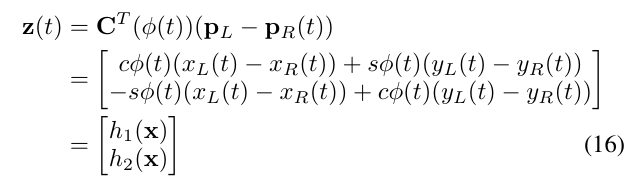
\[ \begin{aligned} C_{wr} p_{L,inR}=P_{L,in w}-P_{R}(t) \\ \Longrightarrow C_{wr} p_{L,inR}+P_{R}(t)=P_{L,in w} \end{aligned} \]
上式就是将机器人坐标系下的路标点转换到世界坐标系的变换,反过来,就是(式16),可以得到机器人坐标系下的路标点的坐标
对式(15)和式(16)中描述的系统模型进行可观测性分析,首先计算所有k阶Lie 微分\(L_{f_j}^k h_i (for k \in \N,j=1,2,i=1,2)\),用\(\mathcal{G}\)来表示。
由\(\mathcal{G}\)各元素的梯度张成的空间\(d\mathcal{G}\)为:
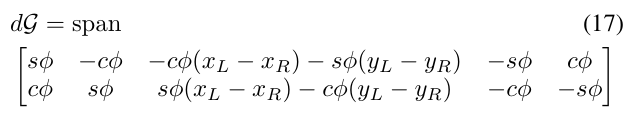
上述矩阵就是非线性SLAM系统的可观测矩阵,显然,这个矩阵的秩是2,因此这个系统是不可观测的。
3.2.1. 补充:引自_崔老师_可观性矩阵的计算
为什么只取到2阶? 意味着n=3? 3个自由度(平移xy+旋转)?
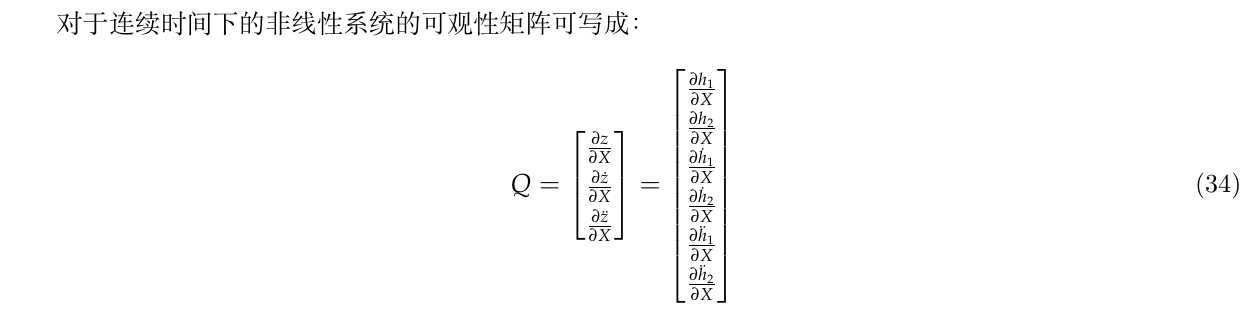
3.2.1.1. 观测z对状态X的雅克比\(\frac{\partial z}{\partial X}\)
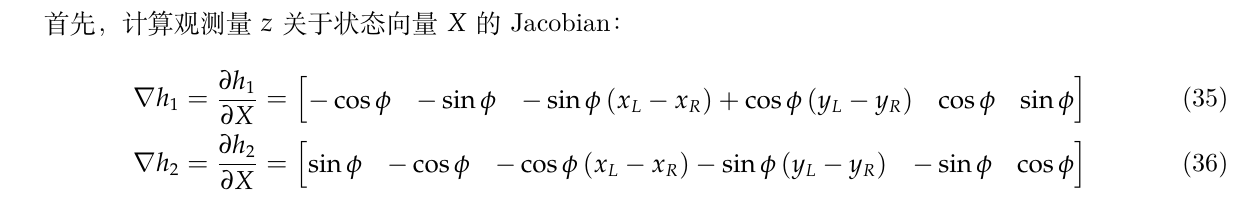
3.2.1.2. {观测值z对时间的导数\(\dot{z}\)}对状态X的雅克比\(\frac{\partial \dot{z}}{\partial X}\)
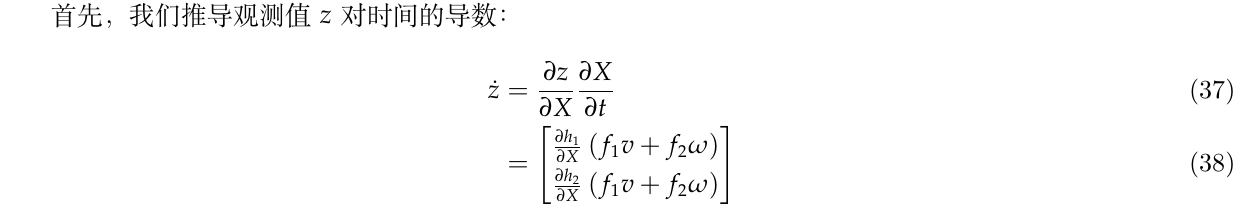
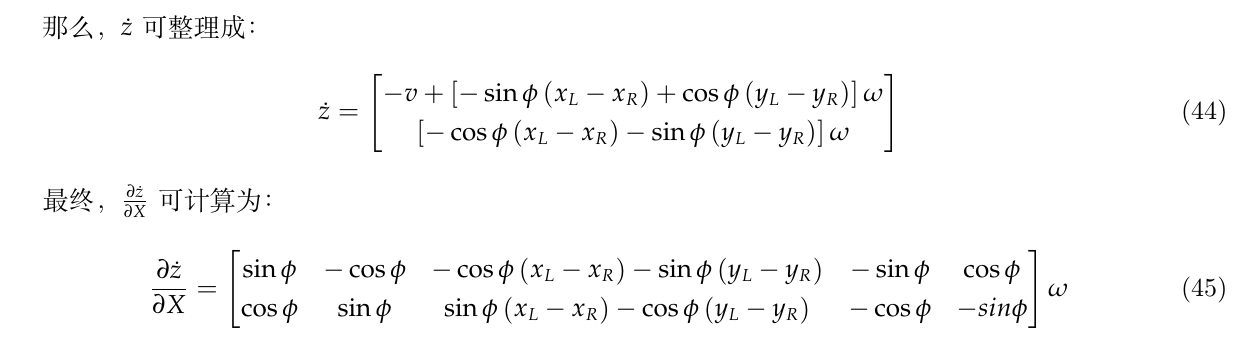
3.2.1.3. {观测值z对时间的二次偏导\(\ddot{z}\)}对状态X的雅克比\(\frac{\partial \ddot{x}}{\partial X}\)

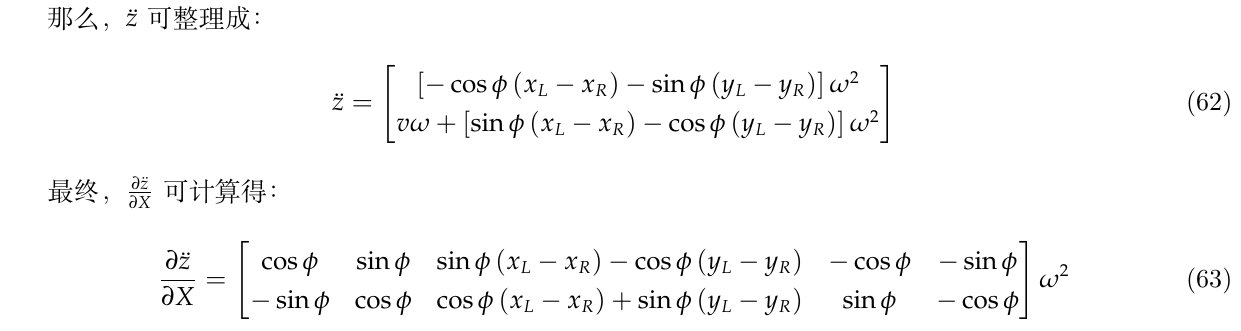
3.2.1.4. 最终得到可观性矩阵

3.3. 不可观测的意义
直觉上,就是我们无法获得绝对的结果,只是从有效测量中获得的相对的状态信息。
尽管不可观测的子空间的概念不能在这个系统中严格定义,通过对\(d\mathcal{G}\)的正交子空间\(d\mathcal{G}\perp\)的基进行物理解释,我们可以获得有用的信息。
通过观察,我们可以看到\(d\mathcal{G}\perp\)空间一种可能的基具有如下形式:
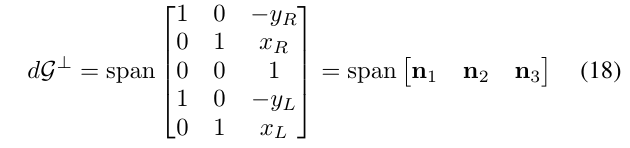
3.3.1. (1) 零空间内平移
从向量n1和n2的结构中我们可以看到状态的变化,即
\[ \Delta x=\alpha n_1 +\beta n_2 \]
这对应于在x轴和y轴上的漂移,x轴上漂移\(\alpha\)个单位,y轴上漂移\(\beta\)单位
因此,如果机器人和地标位置移动相等,则根据测量结果,\(x\)和\(x+\Delta x\)的状态是相等的,即满足\(Hx=0\)和\(H(x+\Delta x)=0\)
3.3.2. (2) 零空间内旋转
为了更好地理解\(n_3\)的物理意义,我们考虑一个情况:
即'x-y'平面通过一个小的旋转量\(\delta \phi\)进行旋转,即受到小扰动。对于平面内所有的点都进行旋转变换,从\(\boldsymbol{x}=[x,y]^T\)变换为\(\boldsymbol{x'}=[x' , y']\),变换等式为:
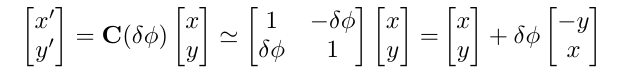
其中,旋转矩阵如下:
\[ \begin{aligned} \begin{bmatrix} \cos \delta \phi & -\sin \delta \phi \\ \sin \delta \phi & \cos \delta \phi \end{bmatrix} \sim \begin{bmatrix} 1 & -\delta \phi \\ \delta \phi & 1 \end{bmatrix} \end{aligned} \]
利用上面这个结果,我们可以看到,如果机器人和路标点所在平面受到小扰动\(\delta \phi\)进行旋转,SLAM系统的状态向量变化如下:
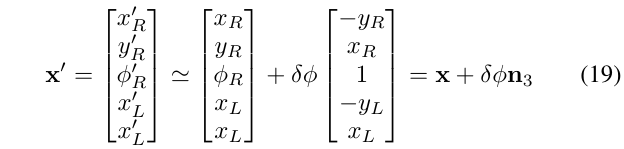
这表明,向量\(n_3\)与x-y平面的旋转相关,因为\(n_3 \in d \mathcal{G} \perp\),这个结果展示了对于旋转量也是不可观测的,因为旋转不会导致观测量的改变。
3.3.3. 结论
在上面的分析中,对\(d \mathcal{G} \perp\)空间的基向量意义的分析,与我们的直觉是一致的,即全局坐标下的状态向量不可观测。