VI中的几种自由度处理方法的性能对比

Catalogue

1. 1. 1. On the Comparison of Gauge Freedom Handling in Optimization-based Visual-Inertial State Estimation
2. 2. 2. 摘要
3. 3. 3. VI问题
   1. 3.1. 3.1. 解的歧义性和几何等价
   2. 3.2. 3.2. 附加约束:指定一个Gauge
4. 4. 4. 处理Gauge
   1. 4.1. 4.1. Rotation Parametrization for Gauge Fixation or Prior
   2. 4.2. 4.2. 处理Gauge Freedom的不同方法
      1. 4.2.1. 4.2.1. gauge fixation approach
      2. 4.2.2. 4.2.2. gauge prior approach
      3. 4.2.3. 4.2.3. free gauge approach
5. 5. 5. 三种处理方式的对比流程
   1. 5.1. 5.1. 数据生成
   2. 5.2. 5.2. 优化求解器
   3. 5.3. 5.3. 评估
6. 6. 6. 对比结果研究
   1. 6.1. 6.1. Gauge Prior: 选择恰当的先验权重
      1. 6.1.1. 6.1.1. Accuracy
      2. 6.1.2. 6.1.2. Computational Cost
      3. 6.1.3. 6.1.3. 讨论
   2. 6.2. 6.2. 准确度和计算量
   3. 6.3. 6.3. 小结
7. 7. 7. 真实世界数据集测试

1. On the Comparison of Gauge Freedom Handling in Optimization-based Visual-Inertial State Estimation

2. 摘要

VI系统中有4个不可观测自由度，绕重力方向的旋转和平移(在本文中称为\(gauge~freedom\))，以及剩下一些可观的自由度，在求解过程中需要进行特殊的处理。 文章对比了以下3种处理方法:

• gauge fixation: 设置不可观测的状态为某个固定的值
• gauge prior: 为某个状态设置先验
• free gauge: 让状态在优化过程中自由演化，优化完成再进行处理

3. VI问题

视觉-惯性状态估计的问题包括对摄像机-惯性组合传感器(IMU)的运动和传感器在场景中运动时摄像机看到的三维地标位置的推断。

通过收集视觉测量方程(图像点)和惯性测量(加速度计和陀螺仪)，问题可写成非线性最小二乘，目标是最小化下面的方程:

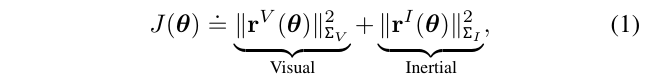
其中

• \(||r||_\Sigma^2=r^T\Sigma^{-1}r\)是残差向量\(r\)的马氏距离
• \(\Sigma\)是测量值的协方差矩阵，作为权重
• 这个cost func 可以作为 "full smoothing"或者"fixed-lag smooth"方法

视觉项由图像观测点\(x_ij\)的重投影误差组成，惯性项包括惯性测量值与IMU轨迹模型预测值(预积分)之间的误差。

问题求解的状态向量如下:

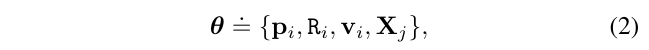
包括摄像机运动参数(外参和线速度)和3D场景(地标)。

加速度计和陀螺仪的bias通常施加在IMU坐标系中，因此不受坐标系固定的影响，因此，我们排除bias，并假设IMU的测量已经纠正。

3.1. 解的歧义性和几何等价

对于VI系统状态估计问题，很重要的一点是，对参数\(\theta\)(或者说状态)给定特殊的变换\(g(\theta)\)，最终的目标函数(cost func)\(J(\theta)\)不变，即:

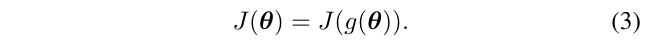
特别的，变换\(g()\)可以用齐次矩阵的形式表达:

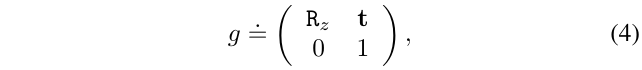
这是一个4自由度的变换，其中:

• \(t \in \R^3\)是任意的平移
• 旋转\(R_z=\exp (\alpha e_z)\)是绕重力方向轴\(e_z=(0,0,1)^T\)的任意yaw角\(\alpha \in (-\pi,\pi)\)所产生的旋转矩阵
• 为了简化表达，使用\(Exp(\theta)=\exp(\theta^\wedge)\)来表示这个变换

通过对状态应用上面的变换\(g(\theta)\)，将得到新的状态\(\theta' \equiv {p_i',R_i',v_i',X_j'}\)

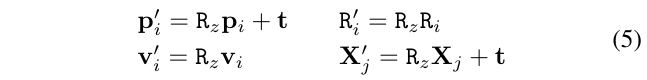
对于\(\theta\)和\(\theta'\)，它们是几何等价的，它们产生相同的误差，即，对于目标函数\(J(\theta)\)，它们最终得到的值是一样的。

作为不变性的结果，参数空间\(\mathcal{M}\)可以分解成几何等价重构的不相交集合(即使用基来表示)，这些几何可以称为\(orbit\)或者\(leaf\)

于是，关于\(\theta\)的\(orbit\)可以如下表示:

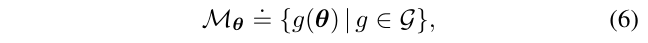
其中,

• \(\mathcal{G}\)是\(g()\)变换的群，注意到目标函数在每一个\(orbit\)上都是常数(意思是存在变换\(g()\)，都不会改变目标函数的值)

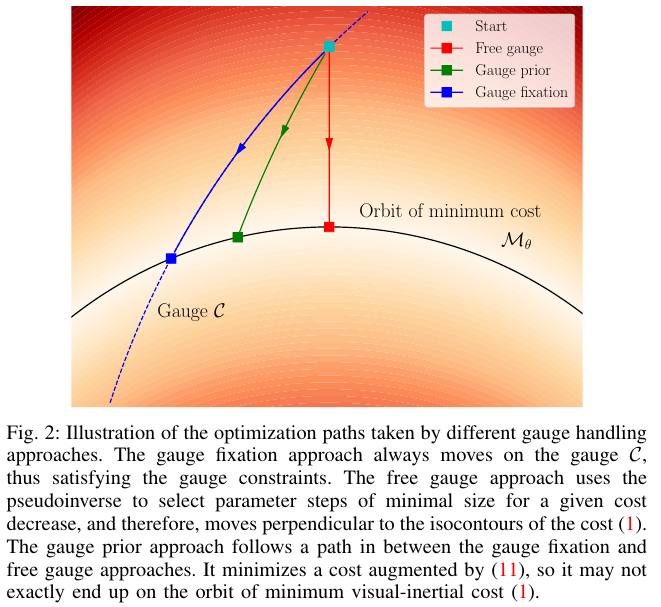
不变性的主要结果是没有一个特定的解，原因是有无穷多个解可以使得目标函数达到同样的最小值，

如下图2: \(orbit\)上的所有状态都可以达到同样的最小值(对于目标函数而言)

因此，VI状态估计问题具有不确定或者说不可观测的状态: 没有足够的方程来完全指定一个唯一解。

上面是三种处理方法关于参数向量维度的对比:

• 总的参数\(n=9N+3K\)，N是相机节点数，K是路标数

3.2. 附加约束:指定一个Gauge

用附加约束完成(1)的处理

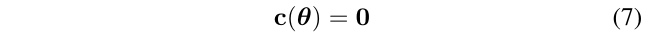
这会产生一个独特的解，称为指定一个\(gauge\)，C

换句话说，就是上面的(等式7)，选择了一个有代表性的\(orbit\)，用来消除等价中的不确定性，在VI系统中，这是通过指定3D的参考坐标系来实现的。

举例: 选择包含第0帧的相机（固定其位姿为position={0,0,0},yaw=0）作为参考坐标系。这些约束指定了一个唯一的转换，因此，这个独特的解就是\(\mathcal{C}\)和参数空间\(\mathcal{M}_\theta\)的并集，即:

\[ \theta_C=\mathcal{C}\cap \mathcal{M}_\theta \]

那么\(gauge\)，C，与轨道\(orbit\)也就是\(\mathcal{M}_\theta\)是横断的，因此，得到的解\(\theta_C\)是唯一的

4. 处理Gauge

从优化的角度来看，使用高斯牛顿来对上面提到的目标函数进行求解会有一些困难，即使我们使用所有元素的最小参数化状态参数向量θ，目标函数中的海森矩阵(用于参数更新的\(H\Delta x\)=b)，由于存在不可观测的自由度，因此是奇异的。

更加具体的说就是，它是一个秩亏矩阵，rank缺了4，恰恰对应了变换\(g()\)中的4个自由度。

上面的Table 1 列出了3种常用的处理方法，其中，

• (gauge fixation approach)是在一个较小的参数空间中进行优化，在这个空间中没有不可观测的状态，因此Hessian是可逆的，这本质上强制了解的硬约束
• (gauge prior approach)是通过附加惩罚(来产生一个可逆的Hessian)来增强目标函数，以使解决方案以一种软的方式满足某些约束
• (free gauge approach)使用H的伪逆，来隐式地为唯一解决方案提供额外的约束(用最小范数更新参数)

前两种策略需要特定于VI问题的知识(需要约束的状态)，而最后一种策略是通用的

4.1. Rotation Parametrization for Gauge Fixation or Prior

使用gauge fixation和gauge prior方法存在一个问题就是，固定相机位姿的1自由度yaw旋转角并不直接。

在使用求解器(如高斯牛顿、LM)迭代时，标准的更新旋转量的方法是:

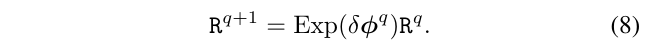
其中，q代表第q次迭代

通过设置\(\delta \phi^q\)中关于\(z\)的元素为0，就可以对\(R^q\)中的yaw角进行固定，然而，如果连接几次这样的更新，如\(R^Q=\prod_{q=0}^{Q-1} Exp(\delta \phi ^q)R^0\)，即相当于经过多次更新之后，并不能把\(R^Q\)的yaw角固定成与\(R^0\)的一致，测试代码如下:

#include <iostream>
#include <eigen3/Eigen/Core>
#include <eigen3/Eigen/Dense>
#include "sophus/so3.hpp"

using namespace std;
int main() {
    Eigen::Matrix3d  R= Eigen::Matrix3d::Identity();
    Sophus::SO3d R_n(R);
    R_n= Sophus::SO3d::exp(Eigen::Vector3d(0.3,0.1,0))*R_n;
    cout<<"First :"<<R_n.log().transpose()<<endl;
    R_n= Sophus::SO3d::exp(Eigen::Vector3d(0.1,0.2,0))*R_n;
    cout<<"Second :"<<R_n.log().transpose()<<endl;
    R_n= Sophus::SO3d::exp(Eigen::Vector3d(0.5,0.1,0))*R_n;
    cout<<"Third :"<<R_n.log().transpose()<<endl;
    return 0;
}

First :   0.3 0.1   0
Second :  0.399579    0.29916 -0.0251046
Third : 0.896385  0.404603 0.0308449

尽管使用yaw-fixation或者使用添加先验的方法可以应用于任何相机位姿，这通常用于第一帧。因此，对于其他帧的相机位姿，我们使用标准的迭代更新，对于第一帧，\(R_0\)，我们使用更加方便的参数。我们不直接使用R0，而是使用左乘增量:

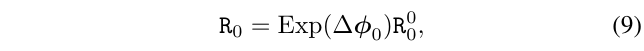
其中，旋转向量\(\Delta \phi_0\)被初始化为0，然后进行迭代更新。然而，旋转向量在\(||\Delta \phi_0||=\pi\)的时候具有奇异，然而在优化的时候，提供的初值应该比较接近真值，即(\(||\Delta \phi_0||<\pi\))，因此可以暂时不过分计较这个问题。

4.2. 处理Gauge Freedom的不同方法

4.2.1. gauge fixation approach

在整个优化过程中，测量固定包括固定第一帧位姿的位置和偏航角，这通过设置如下来实现:

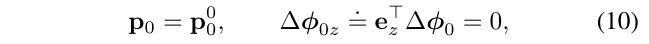
其中\(p_0^0\)是第一帧相机的初始位姿，固定这些参数向量相当于将残差所计算的雅克比矩阵的对应的列置为0，即\(J_{p0}=0\)，\(J_{\Delta 0z}=0\)

4.2.2. gauge prior approach

通过在目标函数(等式1)加入惩罚项:

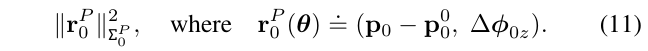
关于\(\Sigma_{0}^P\)的选择在后面讨论

4.2.3. free gauge approach

这个处理方法是让参数向量在优化中自由演化。为了求解这个奇异的Hessian矩阵，我们通过使用伪逆或者是添加一些阻尼(如LM算法)使得最小二乘问题可解。

三种方法优化迭代过程中参数空间路径的比较如图2所示

5. 三种处理方式的对比流程

5.1. 数据生成

我们采用6自由度的轨迹，分别是类正弦波，弧状的，矩形的。考虑两种路标配置：

• 平面的，3D点粗略的分布在几个平面上
• 随机的，3D点随机沿着轨迹生成

图3展示了仿真:

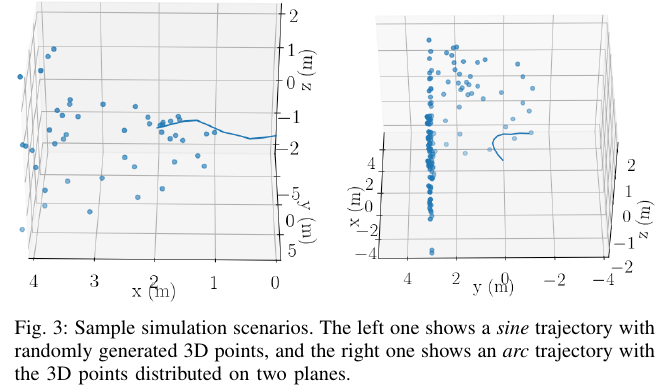
为了生成imu测量值，我们使用B样条拟合轨迹，然后采样出加速度和角速度。采样值会受到bias和额外添加的高斯白噪声影响，然后作为Imu测量值。

对于数据额测量，我们使用pinhole相机模型，将3D点投影到图像上，得到3D-2D的点对，然后也添加高斯白噪声。

5.2. 优化求解器

为了求解VI系统的状体估计问题，使用gogle的Ceres求解器，采用LM算法。然后实现了上面所述的3种对gauge freedoom的处理方式。对于每条轨迹，我们沿着轨迹采样一些关键帧。我们的参数空间包含了这些关键帧的状态(如位置、旋转、和速度)，以及3D点的位置，而初始状态被随机打乱

5.3. 评估

1. 准确率:

   为了评估状态估计值的准确率，我们首先计算了将估计值对齐到真值的变换，这个变换从所有轨迹的第一帧开始计算，这个变换具有4自由度(也就是上面提到的平移和绕重力方向矢量的旋转)。

   对齐之后，我们计算所有关键帧的均方差根(RMSE)，特别的，我们对位置和速度误差使用欧几里得距离来计算。

   对于旋转估计值，我们首先计算估计值和真值的相对旋转量(轴角形式表示)，然后使用相对旋转的角度作为旋转误差。

2. 计算效率:

   为了评估算力消耗，我们记录了求解器的收敛的时间和迭代次数。我们使用每种配置(如轨迹和3D点的结合)，进行50次试验，计算平均时间和精度指标

3. 协方差:

   我们同样比较由优化算法产生的协方差，这些协方差对active SLAM等应用有重要意义。

   参数估计值的协方差由Hessian矩阵的逆确定。(对于free gauge approach，使用摩尔-彭罗斯伪逆，因为Hessian是奇异的)

6. 对比结果研究

6.1. Gauge Prior: 选择恰当的先验权重

在比较3种方法之前，对于Gauge Prior Apporach，首先需要选择先验协方差\(\Sigma_0^P\)。

一种通用的选择是\(\Sigma_0^P=\sigma_0^PI\)，也就是(式11)中的先验变成\(||r_0^P||_{\Sigma_{0}^P}^2=w^P||r_0^P||^2\)，其中\(w^P=\frac{1}{\sigma_0^2}\)

我们测试了大范围的先验权重\(w^P\)，最后得到的结果都是相似的。

需要注意的是，\(w^P=0\)的本质是第三种方法free gauge approach，而\(w^P \rightarrow \infin\)对应的是第一种方法gauge fixation approach

6.1.1. Accuracy

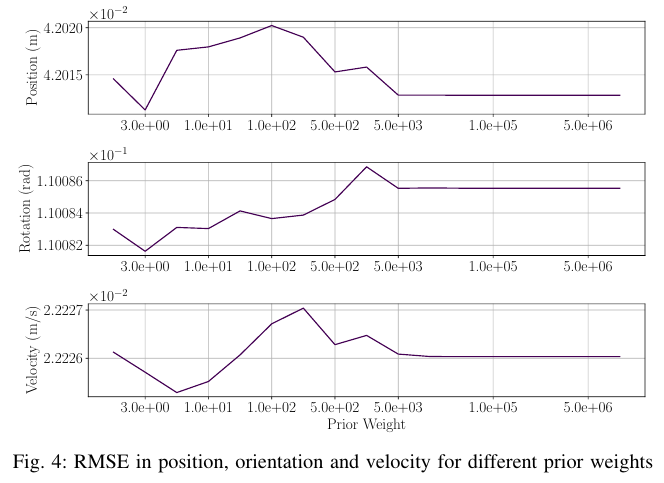
图4展示了随着先验权重变化，RMSE的变化。

可以看出，不同先验权值的估计误差非常相似(注意纵轴上的数字)。虽然对于轨迹和三维点的不同配置没有明确的最优先验权值，但当权值增加到一定的阈值以上时，RMSE稳定在一个值上，如图4则是500

6.1.2. Computational Cost

图5展示了不同先验权重的计算代价，与图4相似，当先验权值大于一定值时，迭代次数和收敛时间趋于稳定。

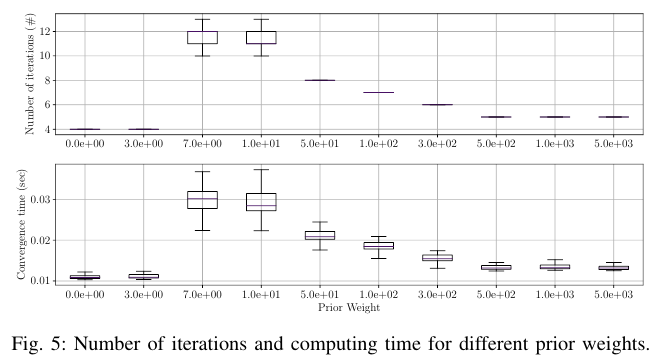
有趣的是，当先前的权重从0增加到稳定的阈值时，在计算时间上有一个峰值，对于所有配置都可以观察到相同的行为。

为了详细研究这一行为，我们在图6中绘制了几个先验权值的每次迭代的平均重投影误差的先验误差，

• 位置先验误差是第一个位置的当前估计值与其初始值之间的欧氏距离
• 偏航先验误差是第一个旋转的当前估计相对于其初始值的相对旋转的z分量
• 平均重投影误差为所有关键帧中观察到的三维点的个数所平均得到的总视觉残差

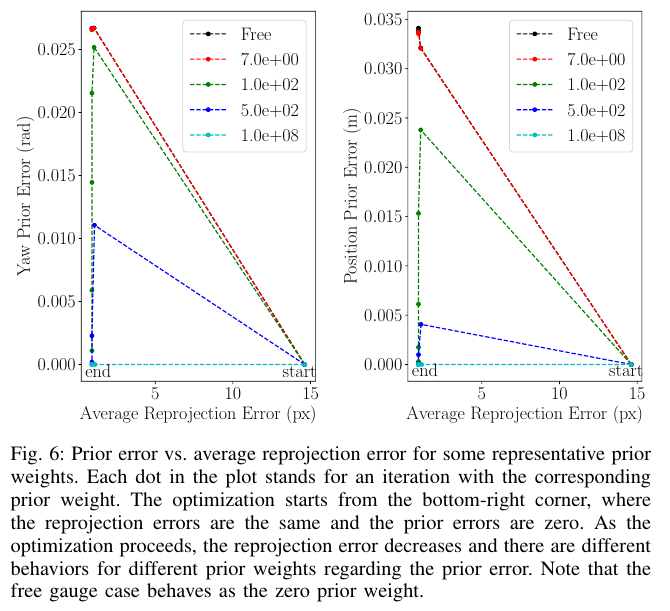
对于非常大的先验权重(\(10^8\))，随着先验误差减少至0，算法同时也减少了重投影误差。

相比之下，对于较小的先验权值(如50-500)，优化算法在前两次迭代中减少了重投影误差，但代价是增加了先验误差，然后，优化算法进行多次迭代，(沿轨道移动)，对先验误差进行微调，同时保持重投影误差较小，因此计算时间增加。

6.1.3. 讨论

对于不同的先验权值，解的精度变化不明显时(如图4)，需要选择适当的先验权重来保持较低的算力消耗(图5).

极大的权值被丢弃，因为它们有时会使优化变得不稳定，对于不同的配置(轨迹和3D点的组合得到各种配置)，我们观察到类似的行为。因此，在接下来的部分，对于gauge prior approach，我们将使用合适的先验权重(如\(10^5\))。

6.2. 准确度和计算量

我们比较了三种方法在六种模拟轨迹(正弦、圆弧和矩形)和三维点(平面和随机)组合上的性能。

我们优化了使用不同扰动来初始化的目标函数，然后观察到结果都是相似的。所选取的扰动如下:

• 真值位置使用5cm的向量进行扰动(对于整条轨迹就是5m)
• 旋转量使用随机旋转6度进行扰动
• 速度使用均匀分布随机扰动[-0.05,0.05]m/s ，(速度均值是2m/s)
• 3D点的位置采用均匀随机变量[-7.5,7.5]cm来进行扰动

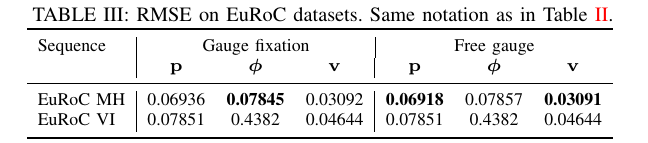
表二列出了50次试验的平均RMSE

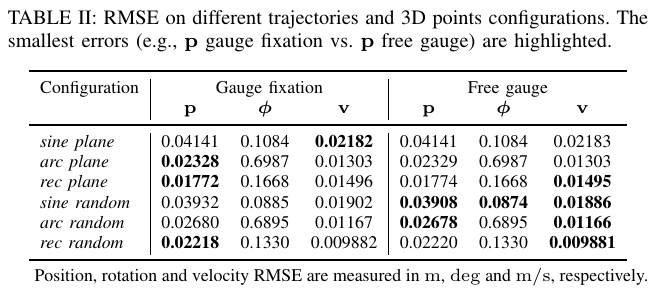
我们省略了gauge prior approach的结果，因为它们与gauge fixation approach在小数点后8位以内的结果相同。

可以看到，在gauge fixation approach和free gauge approach之间仅有很小的差异。

收敛时间和迭代次数如图7所示

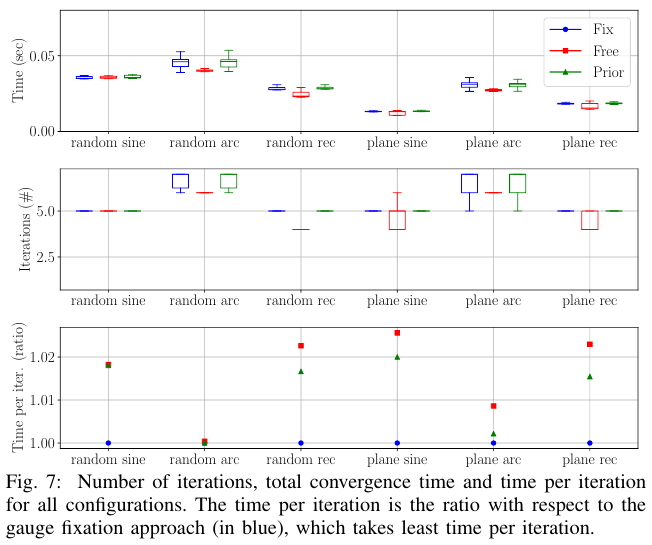
gauge prior approach和gauge fixation approach的计算量大体相同，而第三种方法即free gauge approach比前两者稍微更快一些。

具体来说，除了具有随机三维点的正弦轨迹外，free gauge approach的迭代次数较少，(总体)收敛时间也较短。

有一点需要注意的是: gauge fixation approach由于优化中变量的数量较少，因此每次迭代花费的时间最少

6.3. 小结

• 这三种方法的精确度几乎相同
• gauge prior approach，需要选择合适的先验权重来避免计算量的增大
• 如果选择合适的先验权重，那么gauge prior approach将会与gauge fixation approach具有几乎一致的性能表现(精确度和计算量)
• free gauge approach比其他两种方法稍微快一些，因为它只需更少的迭代次数即可收敛

虽然可以对不可观测的DoFs进行固定(即gauge fixation approach)(回想一下，我们使用了一个定制的参数化方法(9)来固定偏航角)，但是free gauge approach有一个额外的优点，那就是它是通用的

7. 真实世界数据集测试

我们使用EuRoC MAV数据集的两个序列进行了与前面仿真环境相同的实验比较: Machine Hall 1 (MH1) 和 Vicon Room 1 (VI1).

我们使用 semi-direct visual odometry algorithm (SVO)来提供优化问题中参数的初始值，并且使用双目配置的SVO来消除尺度模糊性。对于bias，则直接使用数据集中附带的真值。

评估的方法与上面仿真环境下的一样，需要注意的是: 我们并没有在完整的轨迹上运行优化，而是在更短的段上运行，这足以说明三种方法的不同之处

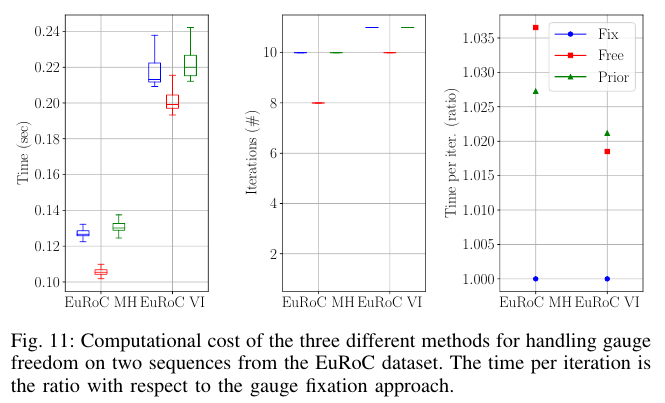
三种不同方法的计算成本如图11所示

准确率由表3展示: 这三种方法都有相似的估计误差