矩阵相关

Catalogue

1. 1. 1. 加法
   1. 1.1. 1.1. 加法性质
2. 2. 2. 数乘
   1. 2.1. 2.1. 数乘性质
3. 3. 3. 转置
   1. 3.1. 3.1. 共轭转置
   2. 3.2. 3.2. 转置性质
4. 4. 4. 对称
5. 5. 5. 矩阵乘法
   1. 5.1. 5.1. 矩阵乘法中的某一行或某一列的计算[Important]
   2. 5.2. 5.2. 矩阵块乘法
   3. 5.3. 5.3. 乘法分配
6. 6. 6. 矩阵的逆
   1. 6.1. 6.1. 矩阵等式
   2. 6.2. 6.2. 如果矩阵的逆存在
   3. 6.3. 6.3. 计算矩阵的逆
   4. 6.4. 6.4. 逆的性质
7. 7. 7. 线性函数
   1. 7.1. 7.1. 线性组合
   2. 7.2. 7.2. 线性系统

1. 加法

1.1. 加法性质

2. 数乘

2.1. 数乘性质

3. 转置

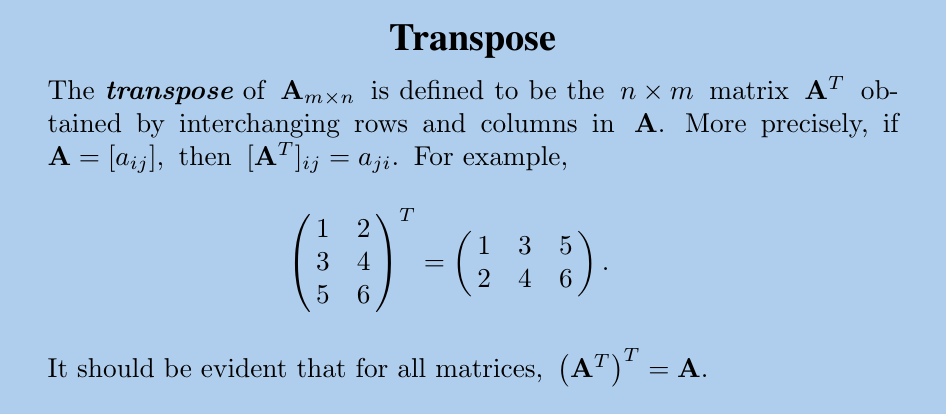
3.1. 共轭转置

3.2. 转置性质

4. 对称

5. 矩阵乘法

5.1. 矩阵乘法中的某一行或某一列的计算[Important]

举例:

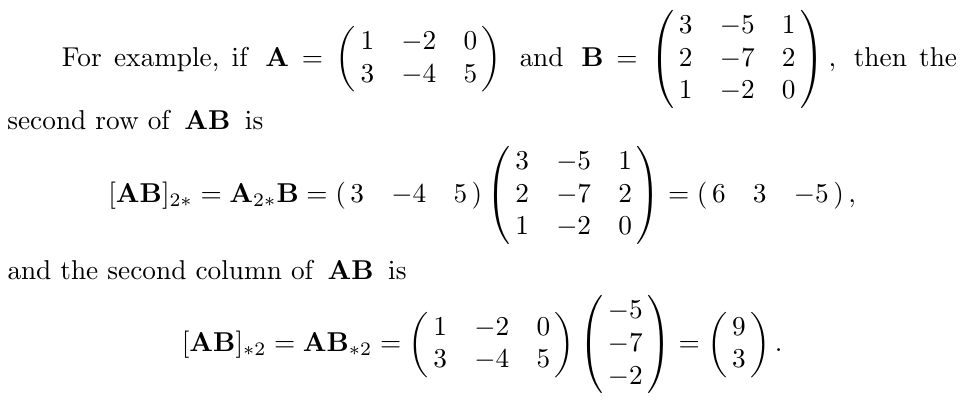
\[ \begin{aligned} [AB]_{2*} &=A_{2*}B \\ &= \begin{bmatrix} \begin{bmatrix} a_{21}*b_{11}+ \\ a_{22}*b_{21}+ \\ a_{23}*b_{31} \end{bmatrix} & \begin{bmatrix} a_{21}*b_{12}+ \\ a_{22}*b_{22}+ \\ a_{23}*b_{32} \end{bmatrix} & \begin{bmatrix} a_{21}*b_{13}+ \\ a_{22}*b_{23}+ \\ a_{23}*b_{33} \end{bmatrix} \end{bmatrix} \\ &= \begin{bmatrix} a_{21}*[b_{11},b_{12},b_{13}]+ \\ a_{22}*[b_{21},b_{22},b_{23}]+ \\ a_{23}*[b_{31},b_{32},b_{33}] \end{bmatrix} \\ &= \begin{bmatrix} a_{21}B_{1*}+ \\ a_{22}B_{2*}+ \\ a_{23}B_{3*} \end{bmatrix}_{1\times 3} \end{aligned} \]

5.2. 矩阵块乘法

5.3. 乘法分配

6. 矩阵的逆

6.1. 矩阵等式

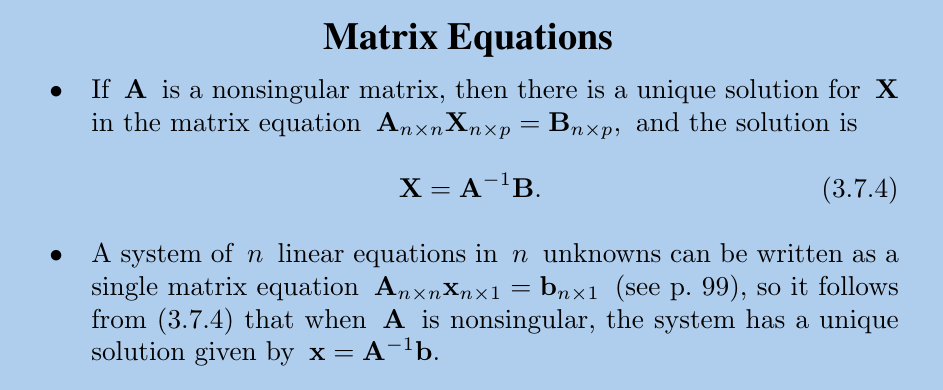
6.2. 如果矩阵的逆存在

则下面几条描述是等价的:

6.3. 计算矩阵的逆

6.4. 逆的性质

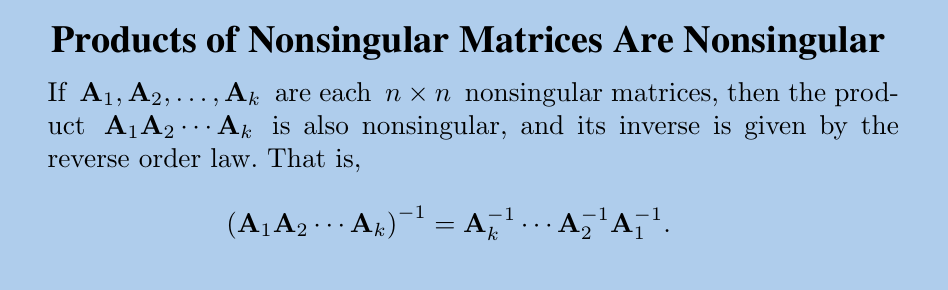
7. 线性函数

7.1. 线性组合

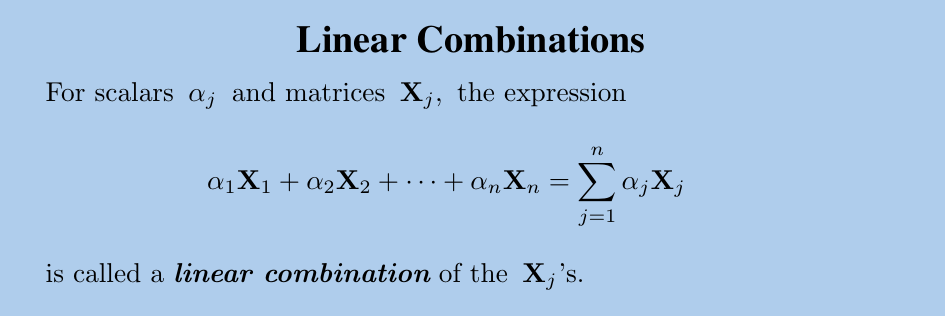
7.2. 线性系统