1. Gauges and Gauge Transformations for Uncertainty Description of Geometric Structure with Indeterminacy

2. 摘要
本文提出了一种一致的理论,用于描述从一系列图像中进行三维重建过程中的确定性和不确定性
首先给出关于gauges和gauge transformations的相关理论,然后讨论了如何评价具有不确定性的解的可靠性,并将克拉美罗下界推广到包含内部不确定性。
另外还介绍了free-gauge approach,然后定义了独立于特定规格的协方差矩阵的标准形式
3. 介绍
从图像中进行3D重建包含了不确定性。
这些不确定性可以通过施加一些normalization的约束来移除,例如:
- 我们可以将坐标原点固定在对象的特定点上,并将对象的大小标准化为单位长度
- 而固定参数则定义为没有不确定性,其他所有参数的不确定性均被改变
4. 3D重建问题
在本文中,我们将重点放在基于特征的方法上: 我们追踪图像序列上的可识别特征点(如角点和标记点)的运动,并利用摄像机投影模型的知识计算它们的三维位置
假设我们在M幅图像上跟踪N个刚性移动的特征点,令\((x_{ka},y_{ka})\)为第k帧的第a个点的像素坐标
这里,我们采用以相机为中心的描述,假设一个物体在场景中相对于静止的相机移动,但是,如果我们将摄像机看作是移动的,并拍摄静止场景的图像,那么后续的分析基本上是相同的。
4.1. 目标函数
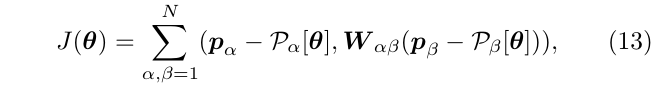
5. Gauges
gauge freedom的存在表明了在参数空间\(\mathcal{M}\)中,存在一个光滑流形,对于任意的点\(\theta\)其给出的解都能使目标函数的值一样。
对于在上述的光滑流形中的两点,\(\theta\)和\(\theta'\)是几何等价的,记为\(\theta \sim \theta'\),其中\(\theta'=g \theta\),\(g()\)代表的是该流形空间(零空间)中的两点的变换关系
这意味着,对于这个等价关系,真正的参数空间不是\(\mathcal{M}\),而是\(\mathcal{M}\)的商空间\(\mathcal{M}/\mathcal{G}\),记为\(\mathcal{M}_\theta\)
例如:\(\mathcal{M}\)的子集包含了所有关于\(\theta\)的等价
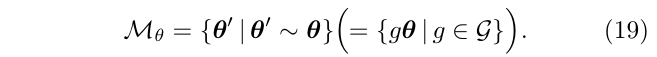
如果gauge的自由度为r,那么\(\mathcal{M}_\theta\)则是参数空间\(\mathcal{M}\)的r维submanifold,并且称为是与参数\(\theta\)相关的叶子
为了消除解的模糊性,我们定义其他流形空间,它与上面的流形相交于一点。
选取特定的\(\theta\)值的一个自然的想法是,对于上面的\(\mathcal{M}_\theta\)分配r个等式:
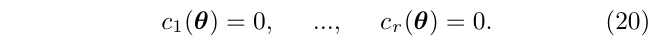
每一个等式去除gauge freedom中的一个自由度,我们称这些等式为gauge condition,如果这些等式满足:
- 它们在代数上是独立的,共同定义了一个在参数空间\(\mathcal{M}\)中的
submanifold\(\mathcal{C}\),称为gauge manifold gauge manifold\(\mathcal{C}\)与参数空间\(\mathcal{M}\)中的所有叶子,即与\(\mathcal{M}_\theta\)相交于一点- 对于任何\(\theta \in \mathcal{M}_\theta\)和\(\theta_C=C \cap \mathcal{M}_\theta\),存在一个独特(仅有一个)的变换g(),使得\(\theta_C=g\theta\)
此后,gauge和gauge manifold都是一个意思,记为\(\mathcal{C}\)
通过引入\(\mathcal{C}\),我们可以找到一个与叶子\(\mathcal{M}_\theta\)的独一无二的交点,并且同时满足目标函数最小值
5.1. gauge fix approach

其中,
- \(t_k\)是平移
- \(s_a\)是尺度
6. 估计的等价性定理
- \(T_{\theta C}(\mathcal{M})\)是参数空间\(\mathcal{M}\)在参数\(\theta_C\)处的正切空间(
tangent space),是一个n维的线性空间 - \(T_{\theta C}(\mathcal{C})\)是
gauge manifold\(\mathcal{C}\)在参数\(\theta_C\)处的正切空间,它是\(T_{\theta C}(\mathcal{M})\)的(n-r)维子空间 - n: 参数向量\(\theta\)的维度数
- r:
gauge freedom的自由度 - n-r: 可观测的维度
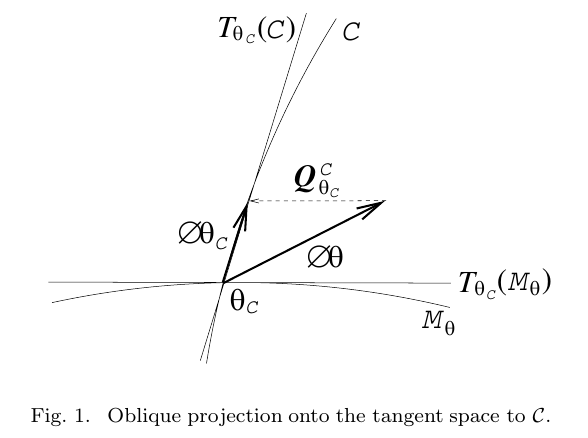
6.1. 图1的个人理解
- 已知在\(M_\theta\)轨道上,任意一点都可以满足使得目标函数\(J()\)最小化
- 假定轨道上某一点\(\theta_C\)处,求得了一个增量\(\phi_\theta\),显然,这个增量有一部分分量不会改变目标函数\(J()\)的能量
- 在点\(\theta_C\)处,存在一个正切流形空间\(T_{\theta_C}(M_\theta)\),增量\(\phi_\theta\)在这个正切空间上的投影量,只会使得\(\theta_C\)点沿着\(M_\theta\)轨道移动,而不是沿着垂直方向移动,因此,这部分分量并不改变目标函数\(J()\)的能量
- 那么这个在点\(\theta_C\)处的正切流形空间\(T_{\theta_C}(M_\theta)\),也就是所说的零空间
6.2. 关于零空间的基
零空间的基,实际上就是正切流形空间\(T_{\theta_C}(M_\theta)\)的基,可以通过在\(M_\theta\)轨道在\(\theta_C\)处使用小量来进行计算,这跟计算切向量的方法一样的
举例: 求\(\theta_C\)处,关于位姿的平移量x值的零空间基

6.3. 等价性的推导
在这一节中,我们定义了在gauge manifold上的斜投影,并证明所有投影到相同点上的扰动在几何上是等价的
设\(\hat{\theta}_C\)是参数\(\theta\)对于gauge \(\mathcal{C}\)的估计。 使用一阶近似,那么作差\(\Delta \theta_C=\hat{\theta}_C-\theta_C\)可以使用\(T_{\theta C}(\mathcal{C})\)中的一个元素来标识
- 注意: \(\hat{\theta}_C\)和\(\theta_C\)都表示状态
- \(\Delta \theta_C\)才表示增量
令\(\Delta \theta \in T_{\theta C}(\mathcal{M})\)是一个任意的向量(也就是下图中的向量1),则有:
当且仅当\(\Delta \theta-\Delta \theta_C \in T_{\theta C}(\mathcal{M}_\theta)\) ,(也就是下图的向量1-向量2,得到向量的\(Q_{\theta_C}^C\)),那么有:
\(\theta_C+\Delta \theta\)与\(\hat{\theta}_C=\theta_C+\Delta \theta_C\)是几何等价的
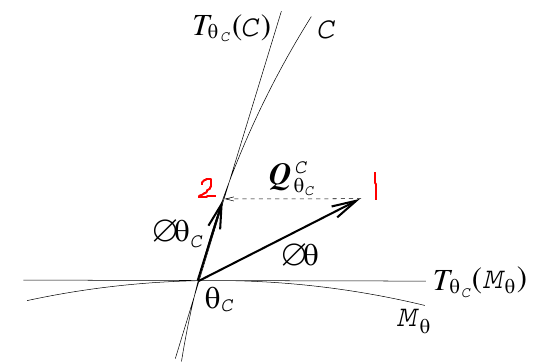
因为\(\{D_1(\theta_C),\cdots,D_r(\theta_C)\}\)是空间\(T_{\theta C}(\mathcal{M}_\theta)\)的基 (零空间的基),那么上面的条件等价于: 存在r个数字\((x_1,\cdots,x_r)\),使得:
\[ \Delta \theta_C=\Delta \theta + \sum_{i=1}^r x_i D_i(\theta_C) \]
或者说
\[ \Delta \theta_C=\Delta \theta + U_{\theta_C} x \tag{36} \]
其中,
- \(x=(x_1,\cdots,x_r)^T\)
- \(U_{\theta_C}=(D_1(\theta_C),\cdots,D_r(\theta_C))\)
如果gauge \(\mathcal{C}\) 由r个等式来定义,即:
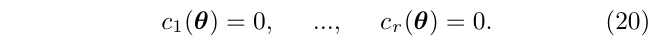
那么,正切空间\(T_{\theta C}(\mathcal{C})\)是

张成的线性空间的正交互补空间
根据\(\triangledown_{\theta C_i}|\theta_C\)和\(\Delta \theta_C\)之间作点乘等于0,对式36两边同时点乘\(V_{\theta_C}\),可以得到:
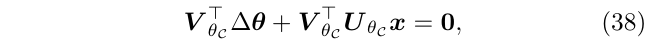
其中,
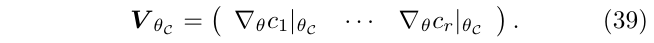
对(式36)和(式38),消去\(x\),可以得到:
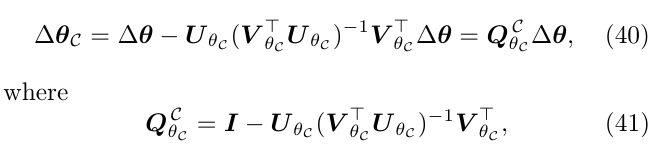
这,就是定义了一个沿着\(T_{\theta C}(\mathcal{M}_\theta)\)到\(T_{\theta C}(\mathcal{C})\)的(斜)投影
因此,得到如下定理:
一个估计\(\hat{\theta}_C\)与\(\theta_C+\Delta \theta\)是几何等价的,当且仅当:
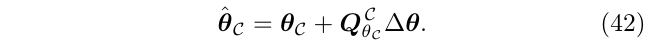
7. 数值优化
问题是给定gauge,如何用数值方法求得最优估计量
牛顿迭代法具有良好的二次收敛性,但同时,解需要满足gauge condiction
目标函数\(J\)通过在gauge \(\mathcal{C}\)下的真值\(\bar{\theta}_C\)附近展开,有:
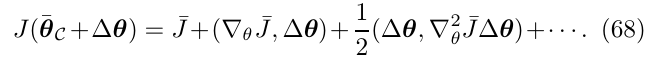
其中,上面的括号\((m,n)\)表示点乘运算
\(\triangledown_{\theta}J,\triangledown_{\theta}^2J\)分别表示目标函数\(J\)对参数\(\theta\)的一阶偏导和二阶偏导
表达式中符号上面的横杠,如\(\bar{J},\triangledown_\theta \bar{J}, \triangledown_\theta^2 \bar{J}\)表示的是在真值\(\bar{\theta}_C\)处进行计算得到的值(也就是线性化点得到值)
\(\Delta \theta\)是使用真值\(\bar{\theta}_C\)处的正切空间\(T_{\bar{\theta}_C(\mathcal{M})}\)的元素来标识的
即\(\Delta \theta\)是在\(T_{\bar{\theta}_C(\mathcal{M})}\)的局部坐标系下的,如 局部扰动向量\(\Delta R_{3\times1}\) (回想四元数的更新,局部扰动)
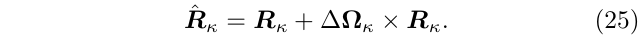
忽略掉目标函数(式68)中的其他高阶项如\(O(\epsilon^3)\),减去在\(\bar{\theta}_C\)处的真值\(\bar{J}\),然后令等式为0,可以得到:
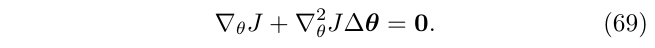
因为Hessian矩阵,即\(\triangledown_{\theta}^2J\)的秩是\(n-r\),这个等式有无穷多个解。
上述(式69),相当于高斯牛顿中的:
\[ \begin{aligned} H\Delta x=b \\ J^T J \Delta x = -J^T r \end{aligned} \]
这里有两种选择,
- 一是通过使用\(r\)条等式与(式69)进行结合(这相当于在目标函数中添加约束项(惩罚项),作为先验):
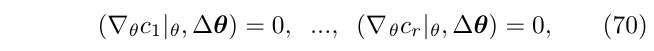
来约束\(\Delta \theta\)在正切空间\(T_{\theta}(\mathcal{C})\),(这是相当于添加先验的方法),由此产生的线性方程组可以确定唯一的解\(\Delta \theta\)
- 另外一种方法是,首先直接计算(式69)的任意一个解
求解的过程中,需要用到伪逆(Moore-Penrose)
然后,根据定理,我们需要利用gauge \(\mathcal{C}\),即用\(Q_{\theta}^C \Delta \theta\)来代替\(\Delta \theta\),最终可以得到:
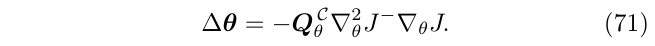
(这个的意思是,先求出一个任意解,然后再减去这个解在零空间上的分量)
Free-Gauge Approach过程可以使用图来描述
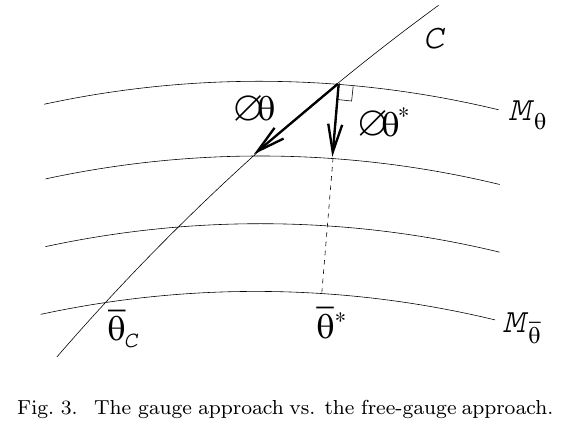
值得注意的是:
Free-Gauge Approach是沿着与\(\mathcal{M}_\theta\)正交的方向去迭代的,因此,其收敛速度会更快一些。