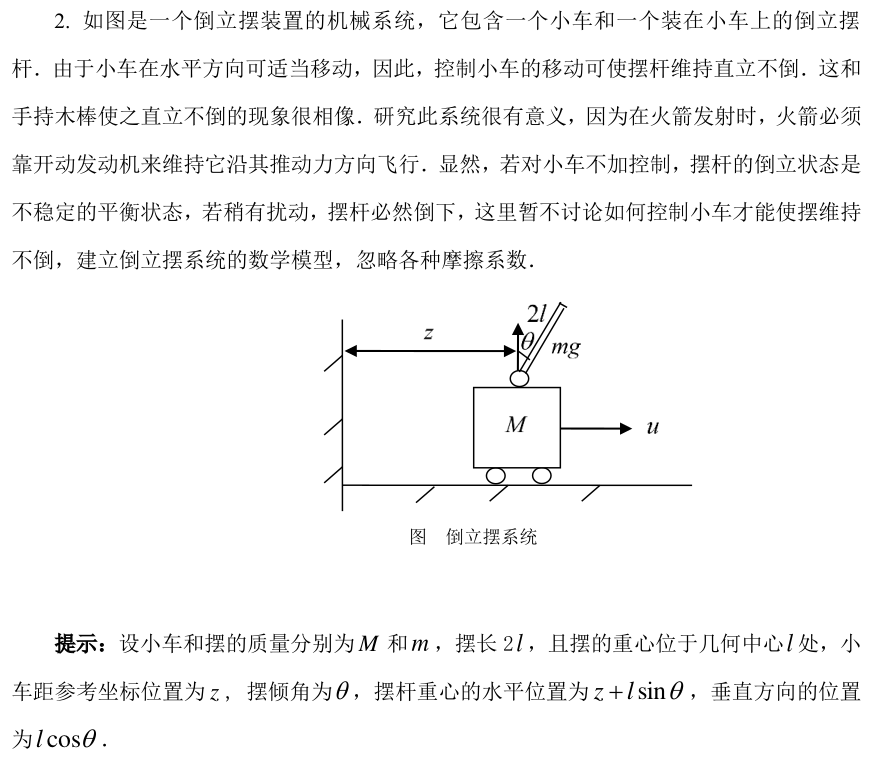
1. 倒立摆案例
2. 法一
2.1. 已知参数
假设:
- 摆的重心坐标\((z+ l\sin \theta,l \cos \theta)\)
- \(\theta\)从垂直向上,向右为正方向
- \(u\)向右为正方向
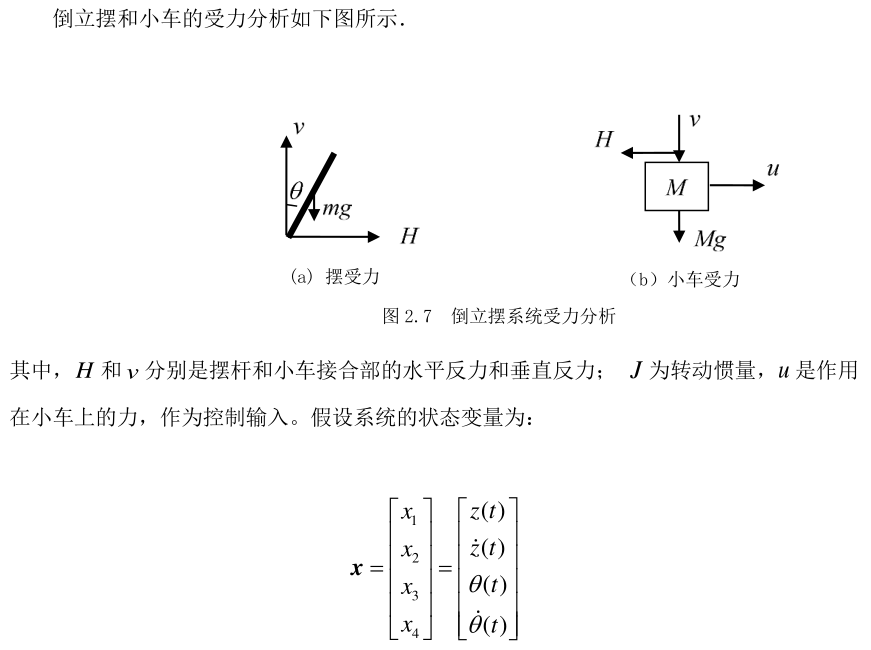
2.2. 对摆进行水平受力分析
摆在水平方向,受到接合处向右的力\(H\)
根据牛顿第二定律,\(F=ma\),有
\[ \begin{aligned} H &=m \frac{d^2(z+l \sin \theta)}{dt^2} \\ &=m\frac{d( \dot{z}+l \cos \theta \dot{ \theta })}{dt} \\ &=m( \ddot{z}+l \cos\theta \ddot{ \theta}-\sin\theta \dot{ \theta}^2) \\ &=m\ddot{z}+ml\cos\theta\ddot{ \theta }-ml\sin\theta\dot{ \theta }^2 \end{aligned} \tag{1} \]
2.3. 对车进行水平受力分析
根据牛顿第二定律,\(F=ma\),有
\[ \begin{aligned} u-H=M\ddot{z} \tag{2} \end{aligned} \]
将(1)带入(2),得到
\[ \Rightarrow u=(M+m)\ddot{z}++ml\cos\theta\ddot{\theta}-ml\sin\theta\dot{\theta}^2 \tag{3} \]
2.4. 对摆进行竖直方向受力分析
根据牛顿第二定律,\(F=ma\),有
\[ \begin{aligned} v-mg&=m\frac{d^2(l\cos\theta)}{dt^2} \\ &=m\frac{d(l(-\sin \theta \dot{\theta}))}{dt} \\ &=ml(-\cos \theta \dot{\theta}^2 - \sin \theta \ddot{\theta}) \\ &=ml\sin \theta \ddot{\theta} - ml \cos \theta \dot{\theta}^2 \end{aligned} \tag{4} \]
2.5. 对摆进行转矩平衡分析
在这里,将摆视为绕着杆的重心旋转,那么,杆在端点(也就是接合处)受到的力沿杆方向进行分解,可以得到两个作用相反的力,分别为\(H\cos \theta\)和\(v \sin \theta\),不难发现,\(H\cos \theta\)使的角\(\theta\)减小,而\(v \sin \theta\)使\(\theta\)增大
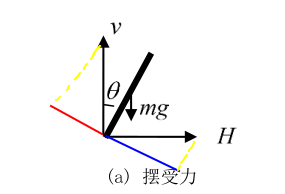
根据转矩平衡,和外力转矩 = 转动惯量 * 角加速度,即有\(M=J\alpha\),得:
\[ vl\sin \theta - Hl \cos \theta = J \ddot{\theta} \tag{5} \]
又根据(1)和(4),
\[ \left \{ \begin{aligned} H=m\ddot{z}+ml\cos\theta\ddot{\theta}-ml\sin\theta\dot{\theta}^2 \\ v=mg+ml\sin \theta \ddot{\theta} - ml \cos \theta \dot{\theta}^2 \end{aligned} \right. \]
代入式(5),得到
\[ \begin{aligned} -m\ddot{z}l\cos \theta - ml^2(\cos^2 \theta-\sin^2 \theta)\ddot{\theta}+mgl\theta = J \ddot{\theta} \end{aligned} \tag{6} \]
2.6. 近似化简
\(\theta\)很小的时候,近似有
\[ \begin{aligned} \cos \theta = 1 \\ \sin \theta =\theta \\ (\frac{d \theta}{dt})^2=\dot{\theta}^2 \approx0 \end{aligned} \]
因此,将式(3)和式(6)进行化简,有:
\[ \left \{ \begin{aligned} u=(M+m)\ddot{z}+ml \ddot{\theta} \\ (J+ml^2)\ddot{\theta}=-ml\ddot{z}+mgl\theta \end{aligned} \right . \tag{7} \]
求解方程组(7),最终,可以得到系统的状态空间描述:
\[ \begin{aligned} \dot{X}= \begin{bmatrix} \dot{z} \\ \ddot{z} \\ \dot{\theta} \\ \ddot{\theta} \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & \frac{-m^2gl^2}{J(M+m)+Mml^2} & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & \frac{mgl(M+m)}{J(M+m)+Mml^2} & 0 \end{bmatrix} \begin{bmatrix} z \\ \dot{z} \\ \theta \\ \dot{\theta} \end{bmatrix} + \begin{bmatrix} 0 \\ \frac{J+ml^2}{J(M+m)+Mml^2} \\ 0 \\ \frac{-ml}{J(M+m)+Mml^2} \end{bmatrix} u \end{aligned} \tag{8} \]
进一步地,如果杆是均匀质杆,那么有转动惯量\(J=\frac{ml^2}{3}\),
代入到式(7)的第二个方程,有
\[ \begin{aligned} (\frac{ml^2}{3}+ml^2)\ddot{\theta}=-ml\ddot{z}+mgl\theta \end{aligned} \tag{9} \]
即可求出\(\ddot{\theta}\)的表达
\[ \ddot{\theta}=\frac{3g}{4l}\theta-\frac{3}{4l}\ddot{z} \]
如果令输入\(u=\ddot{z}\),那么,状态方程可以写成
\[ \begin{aligned} \dot{X}= \begin{bmatrix} \dot{z} \\ \ddot{z} \\ \dot{\theta} \\ \ddot{\theta} \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & \frac{3g}{4l} & 0 \end{bmatrix} \begin{bmatrix} z \\ \dot{z} \\ \theta \\ \dot{\theta} \end{bmatrix} + \begin{bmatrix} 0 \\ 1 \\ 0 \\ \frac{-3}{4l} \end{bmatrix} u \end{aligned} \tag{8} \]
3. 法二
拉格朗日约束法
因此,假设有某个广义坐标\(q\)以及拉格朗日算子\(L\),则拉格朗日方程可表示为:
\[ \frac{d}{dt}(\frac{d L}{d \dot{q}})-\frac{d L}{d q}=f \]
其中,f为沿着广义坐标轴方向上的外力。
对于上述系统,定义由\(z,\theta\)组成的广义坐标系,T为系统的动能,V为系统的是势能。
3.1. 小车动能
\[ T_M=\frac{1}{2}M\dot{z}^2 \tag{9} \]
3.2. 杆动能
\[ \begin{aligned} T_m&=\frac{1}{2}mv^2+\frac{1}{2}J\dot{\theta}^2 \\ &=\frac{1}{2}m\{\underbrace{[\frac{d(z+l\sin \theta)}{dt}]^2}_{v_x}+\underbrace{[\frac{d(l\cos \theta)}{dt}]^2}_{v_y}\}+\frac{1}{2}J\dot{\theta}^2 \end{aligned} \tag{10} \]
3.3. 系统总动能
\[ \begin{aligned} T=T_M+T_m &=\frac{1}{2}M\dot{z}^2+\frac{1}{2}mv^2+\frac{1}{2}J\dot{\theta}^2 \\ &=\frac{1}{2}M\dot{z}^2+\frac{1}{2}m\{\underbrace{[\frac{d(z+l\sin \theta)}{dt}]^2}_{v_x}+\underbrace{[\frac{d(l\cos \theta)}{dt}]^2}_{v_y}\}+\frac{1}{2}J\dot{\theta}^2 \\ &=\frac{1}{2}M\dot{z}^2+\frac{1}{2}m\dot{z}^2+m\dot{z}\cos \theta \dot{\theta}+\frac{2}{3}ml^2\theta^2 \end{aligned} \tag{11} \]
3.4. 系统总势能
\[ V=mgl\cos \theta \]
3.5. 构造拉格朗日约束
拉格朗日算子
\[ \begin{aligned} L=T-V= \frac{1}{2}M\dot{z}^2+\frac{1}{2}m\dot{z}^2+m\dot{z}\cos \theta \dot{\theta}+\frac{2}{3}ml^2\theta^2 - mgl\cos \theta \end{aligned} \tag{12} \]
由于在广义坐标轴\(\theta\)上没有外力作用,因此f=0,所以有s拉格朗日方程:
\[ \frac{d}{dt}(\frac{d L}{d \dot{\theta}})-\frac{d L}{d \theta}=0 \tag{13} \]
需计算如下
\[ \frac{d L}{d \theta}=-m\dot{z}l \sin \theta \dot{\theta}+ mgl \sin \theta \tag{14} \]
\[ \frac{d L}{d \dot{\theta}}=m\dot{z}l\cos\theta+\frac{4}{3}ml^2\dot{\theta} \tag{15} \]
\[ \frac{d}{dt}(\frac{d L}{d \dot{\theta}}) = m\ddot{z}\cos \theta - m \dot{z}l\sin \theta \dot{\theta}+\frac{4}{3}ml^2\ddot{\theta} \tag{16} \]
将式(14)(15)(16)代入式(13),并且使用近似\(\cos \theta=1 , \sin \theta=\theta\),因此有
\[ m\ddot{z}l+\frac{4}{3}ml^2\ddot{\theta}-mgl\theta=0 \tag{17} \]
3.6. 系统状态空间表达
选取系统状态变量\(X\)
\[ \begin{aligned} X= \begin{bmatrix} z \\ \dot{z} \\ \theta \\ \dot{\theta} \end{bmatrix}~~~ Y= \begin{bmatrix} z \\ \theta \end{bmatrix} \end{aligned} \]
如果令输入\(u=\ddot{z}\),那么,根据式(17),状态方程可以写成
\[ \begin{aligned} \dot{X}= \begin{bmatrix} \dot{z} \\ \ddot{z} \\ \dot{\theta} \\ \ddot{\theta} \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & \frac{3g}{4l} & 0 \end{bmatrix} \begin{bmatrix} z \\ \dot{z} \\ \theta \\ \dot{\theta} \end{bmatrix} + \begin{bmatrix} 0 \\ 1 \\ 0 \\ \frac{-3}{4l} \end{bmatrix} u \end{aligned} \tag{18} \]
\[ \begin{aligned} Y= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} z \\ \dot{z} \\ \theta \\ \dot{\theta} \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \end{bmatrix} u \end{aligned} \tag{19} \]
3.7. 能观性能控性分析
已知系统状态方程:
\[ \begin{aligned} \dot{X}= \begin{bmatrix} \dot{z} \\ \ddot{z} \\ \dot{\theta} \\ \ddot{\theta} \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & \frac{3g}{4l} & 0 \end{bmatrix} \begin{bmatrix} z \\ \dot{z} \\ \theta \\ \dot{\theta} \end{bmatrix} + \begin{bmatrix} 0 \\ 1 \\ 0 \\ \frac{-3}{4l} \end{bmatrix} u \end{aligned} \]
\[ \begin{aligned} Y= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} z \\ \dot{z} \\ \theta \\ \dot{\theta} \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \end{bmatrix} u \end{aligned} \]
3.7.1. 构造能观性判别矩阵
\[ \begin{aligned} \begin{bmatrix} C \\ CA \\ CA^2 \\ CA^3 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ - & - & - & - \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ - & - & - & - \\ 0 & 0 & 0 & 0 \\ 0 & 0 & \frac{3g}{4l} & 0 \\ - & - & - & - \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{3g}{4l} \\ \end{bmatrix} \end{aligned} \]
可得,(实际上,仅需要算到CA的时候,就可以判断rank=4了)
\[ \begin{aligned} rank \begin{bmatrix} C \\ CA \\ CA^2 \\ CA^3 \end{bmatrix}=4 \end{aligned} \]
因此,系统完全能观
3.7.2. 构造能控性判别矩阵
\[ \begin{aligned} \begin{bmatrix} B & AB & A^2b & A^3B \end{bmatrix} = \begin{bmatrix} 0 & 1-\frac{3}{4l} & 0 & \frac{-9g}{16l^2} \\ 1 & 0 & 0 & 0 \\ 0 & -\frac{3}{4l} & 0 & \frac{-9g}{16l^2} \\ -\frac{3}{4l} & 0 & \frac{-9g}{16l^2} & 0 \end{bmatrix} \end{aligned} \]
\[ \begin{aligned} rank \begin{bmatrix} B & AB & A^2b & A^3B \end{bmatrix}=4 \end{aligned} \]
因此,系统完全能控
3.8. 稳定性分析
该一级倒立摆系统的状态空间方程为
\[ \left \{ \begin{aligned} \dot{x}(t)=Ax(t)+Bu(t) \\ y(t)=Cx(t)+Du(t) \end{aligned} \right . \]
可知,原系统是非线性系统,在平衡点处进行线性化,得到
\[ \begin{aligned} \dot{X}= \begin{bmatrix} \dot{z} \\ \ddot{z} \\ \dot{\theta} \\ \ddot{\theta} \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & \frac{3g}{4l} & 0 \end{bmatrix} \begin{bmatrix} z \\ \dot{z} \\ \theta \\ \dot{\theta} \end{bmatrix} + \begin{bmatrix} 0 \\ 1 \\ 0 \\ \frac{-3}{4l} \end{bmatrix} u \end{aligned} \]
\[ \begin{aligned} Y= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} z \\ \dot{z} \\ \theta \\ \dot{\theta} \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \end{bmatrix} u \end{aligned} \]
取以下参数
- \(g=9.8m/s^2\)
- \(l=0.25m\)
可以得到系统矩阵A如下
\[ \begin{aligned} A= \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 29.4 & 0 \end{bmatrix} \end{aligned} \]
利用特征方程\(det(\lambda I-A)=0\),可以计算出矩阵A的特征值:
\[ \lambda_{1,2}=0, \lambda_{3,4}=\pm 5.42 \]
因此,可以看到,系统有两个为0的特征根,另外两个特征根一个在复平面左侧,另外一个具有正的实部,根据Lyapunov第一法稳定判据,可以判断,原系统不稳定。