控制相关线性系统理论
Source
Edit
History

第五章-线性系统的能控性和能观性

Catalogue
  1. 1. 1. 线性系统的能控性和能观性
    1. 1.1. 1.1. 例子
  2. 2. 2. 定义
    1. 2.1. 2.1. 状态能控性
    2. 2.2. 2.2. 状态能观性
  3. 3. 3. 线性连续时间系统能控性判据
    1. 3.1. 3.1. 线性定常系统能控性判据
      1. 3.1.1. 3.1.1. 格拉姆矩阵判据(Gram)
      2. 3.1.2. 3.1.2. 秩判据
        1. 3.1.2.1. 3.1.2.1. 例子1
        2. 3.1.2.2. 3.1.2.2. 例子2
      3. 3.1.3. 3.1.3. PBH秩判据(Popov-Belevitch-Hautus)
        1. 3.1.3.1. 3.1.3.1. 例子
      4. 3.1.4. 3.1.4. 约当规范形判据
        1. 3.1.4.1. 3.1.4.1. 例子1
        2. 3.1.4.2. 3.1.4.2. 例子2
    2. 3.2. 3.2. 线性时变系统能观性判据
      1. 3.2.1. 3.2.1. 格拉姆矩阵判据(Gram)
      2. 3.2.2. 3.2.2. 秩判据
        1. 3.2.2.1. 3.2.2.1. 例子
  4. 4. 4. 线性连续时间系统的能观性判据
    1. 4.1. 4.1. 线性定常系统
      1. 4.1.1. 4.1.1. 格拉姆矩阵判据(Gram)
      2. 4.1.2. 4.1.2. 秩判据
      3. 4.1.3. 4.1.3. PBH秩判据(Popov-Belevitch-Hautus)
      4. 4.1.4. 4.1.4. 约当规范形判据
        1. 4.1.4.1. 4.1.4.1. 例子1
        2. 4.1.4.2. 4.1.4.2. 例子2
        3. 4.1.4.3. 4.1.4.3. 例子3
        4. 4.1.4.4. 4.1.4.4. 例子4
        5. 4.1.4.5. 4.1.4.5. 例子5
    2. 4.2. 4.2. 线性时变系统能观性判据
      1. 4.2.1. 4.2.1. 格拉姆矩阵判据(Gram)
      2. 4.2.2. 4.2.2. 秩判据
  5. 5. 5. 线性离散系统的能控性和能观性判据
    1. 5.1. 5.1. 离散系统能控性
      1. 5.1.1. 5.1.1. 线性时变离散系统——格拉姆矩阵判据
      2. 5.1.2. 5.1.2. 线性定常离散系统——秩判据
    2. 5.2. 5.2. 离散系统能观性
      1. 5.2.1. 5.2.1. 线性时变离散系统——格拉姆矩阵判据
      2. 5.2.2. 5.2.2. 线性定常离散系统——秩判据
    3. 5.3. 5.3. 统离散化后保持能控和能观的条件
      1. 5.3.1. 5.3.1. 例子1
      2. 5.3.2. 5.3.2. 例子2
  6. 6. 6. 线性系统能控性与能观测性的对偶关系
  7. 7. 7. 能控标准形和能观测标准形
    1. 7.1. 7.1. 能控规范型
      1. 7.1.1. 7.1.1. 例子
    2. 7.2. 7.2. 能观规范型
      1. 7.2.1. 7.2.1. 例子
  8. 8. 8. 系统的能控性、能观测性和传递函数阵的关系
    1. 8.1. 8.1. 系统的结构分解
      1. 8.1.1. 8.1.1. 按能控性分解
        1. 8.1.1.1. 8.1.1.1. 非奇异变换矩阵T的选取
        2. 8.1.1.2. 8.1.1.2. 例子
      2. 8.1.2. 8.1.2. 按能观性分解
        1. 8.1.2.1. 8.1.2.1. 非奇异变换矩阵T的选取
        2. 8.1.2.2. 8.1.2.2. 例子
      3. 8.1.3. 8.1.3. 规范分解定理
        1. 8.1.3.1. 8.1.3.1. 传递函数矩阵的最小多项式表示形式
      4. 8.1.4. 8.1.4. 传递函数中零、极点相消定理
        1. 8.1.4.1. 8.1.4.1. 例子

1. 线性系统的能控性和能观性

能控性和能观测性是现代控制理论中两个很重要的基础性概念，最优控制和最佳估计都是以它们的存在为条件的，是由 Kalmen（卡尔曼）1960年首先提出的。

可控性和可观测性就是回答“系统的状态是否能控制“和”状态的变化能否由输出测量出来这两个问题。

1.1. 例子

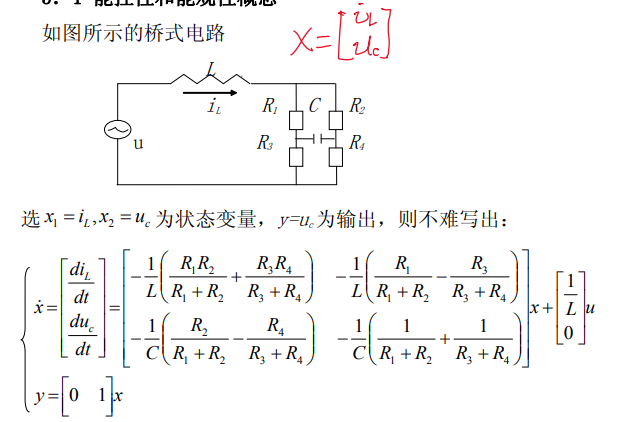
  • \(x2=u_c\)不能控
  • \(x_1=i_L\)不能观

2. 定义

2.1. 状态能控性

2.2. 状态能观性

3. 线性连续时间系统能控性判据

3.1. 线性定常系统能控性判据

假设有线性定常系统

\[ \left \{ \begin{aligned} &\dot{x}=Ax+Bu \\ &x(0)=x_0 \end{aligned} \right. \]

3.1.1. 格拉姆矩阵判据(Gram)

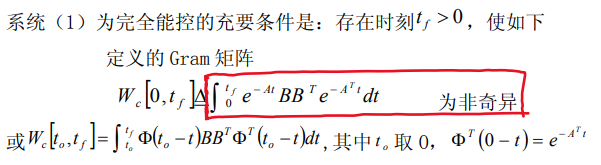
充要条件

  • 格拉姆矩阵非奇异

3.1.2. 秩判据

3.1.2.1. 例子1

3.1.2.2. 例子2

3.1.3. PBH秩判据(Popov-Belevitch-Hautus)

3.1.3.1. 例子

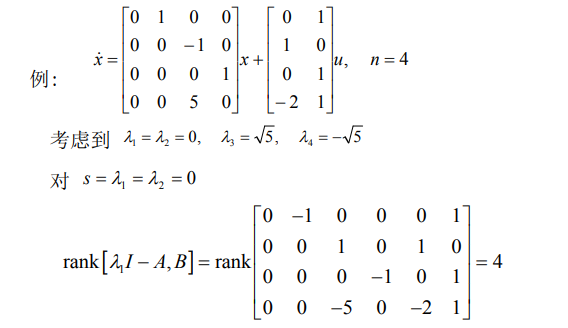
3.1.4. 约当规范形判据

3.1.4.1. 例子1

3.1.4.2. 例子2

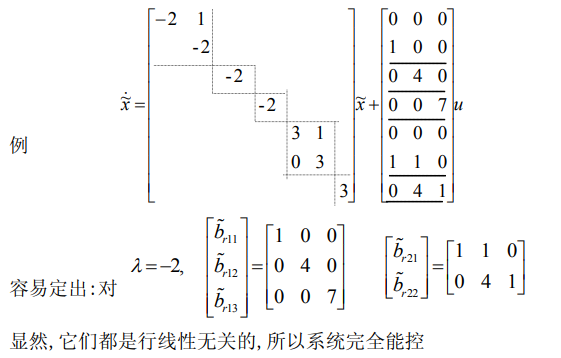
3.2. 线性时变系统能观性判据

设有线性时变系统

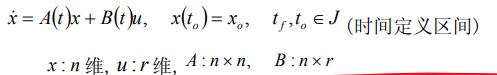
3.2.1. 格拉姆矩阵判据(Gram)

3.2.2. 秩判据

3.2.2.1. 例子

4. 线性连续时间系统的能观性判据

4.1. 线性定常系统

设有线性定常系统

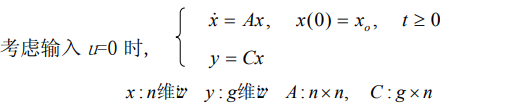
4.1.1. 格拉姆矩阵判据(Gram)

4.1.2. 秩判据

4.1.3. PBH秩判据(Popov-Belevitch-Hautus)

4.1.4. 约当规范形判据

4.1.4.1. 例子1

4.1.4.2. 例子2

4.1.4.3. 例子3

4.1.4.4. 例子4

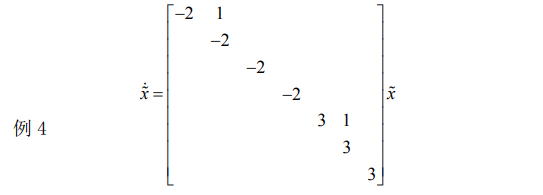
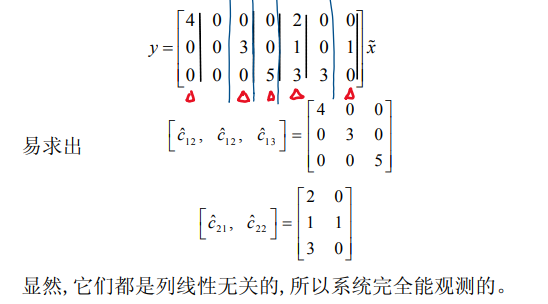
4.1.4.5. 例子5

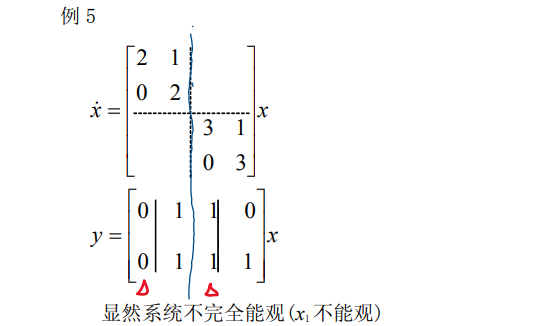
4.2. 线性时变系统能观性判据

假设有线性时变系统

\[ \left \{ \begin{aligned} &\dot{x}=A(t)x , x(t_0)=x_0, t,t_0 \in J \\ &y=C(t)x \end{aligned} \right. \]

4.2.1. 格拉姆矩阵判据(Gram)

4.2.2. 秩判据

5. 线性离散系统的能控性和能观性判据

5.1. 离散系统能控性

5.1.1. 线性时变离散系统——格拉姆矩阵判据

5.1.2. 线性定常离散系统——秩判据

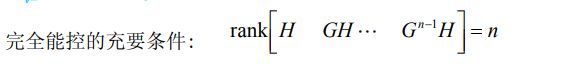
5.2. 离散系统能观性

假设有线性离散系统

\[ \left \{ \begin{aligned} &x(k+1)=G(k)x(k) \\ &y(k)=C(k)x(k) \end{aligned} \right. \]

5.2.1. 线性时变离散系统——格拉姆矩阵判据

5.2.2. 线性定常离散系统——秩判据

5.3. 统离散化后保持能控和能观的条件

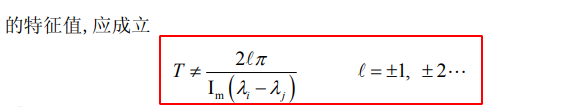
5.3.1. 例子1

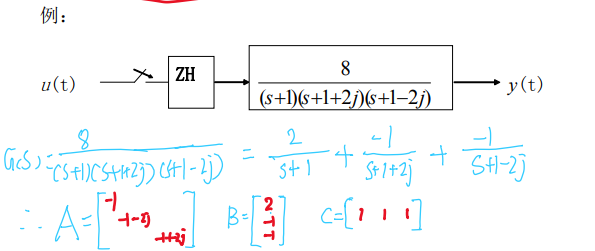
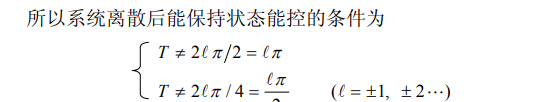
5.3.2. 例子2

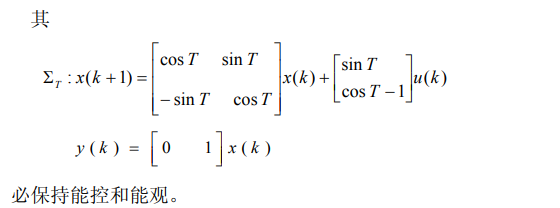
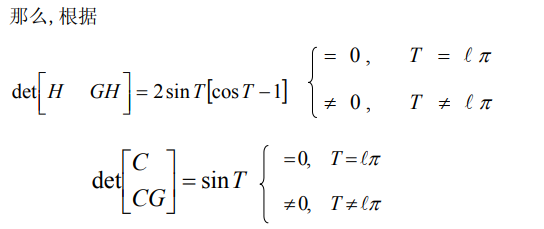
6. 线性系统能控性与能观测性的对偶关系

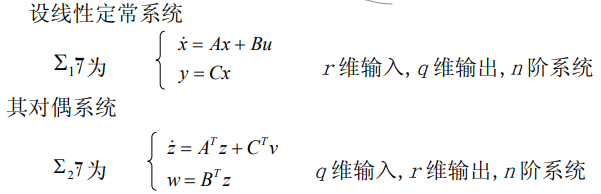
7. 能控标准形和能观测标准形

7.1. 能控规范型

7.1.1. 例子

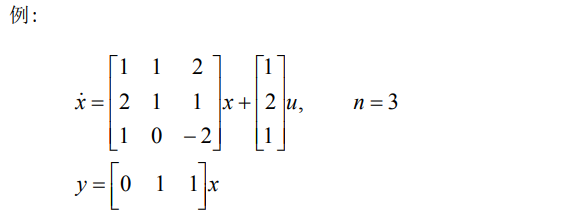
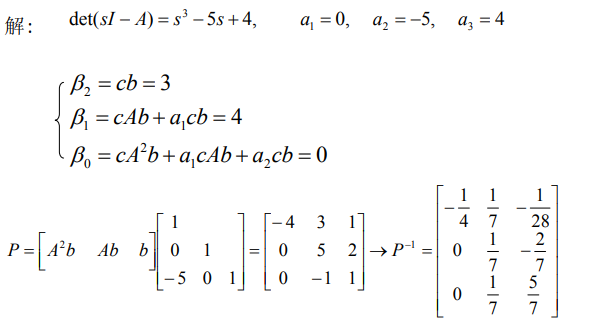
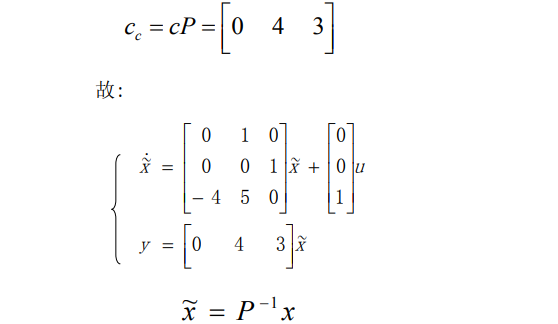
7.2. 能观规范型

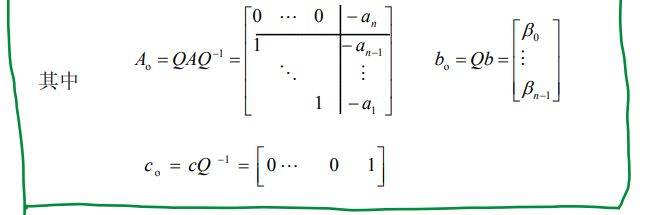
7.2.1. 例子

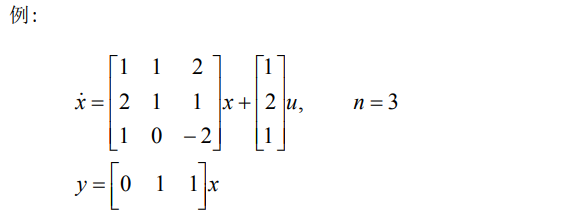
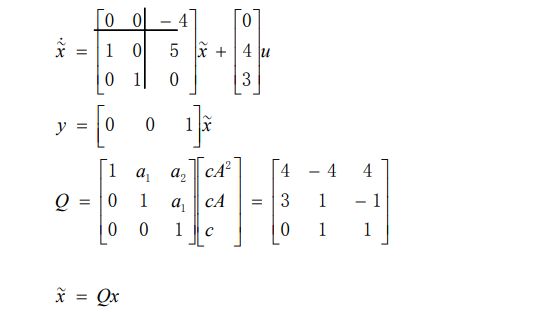
8. 系统的能控性、能观测性和传递函数阵的关系

8.1. 系统的结构分解

8.1.1. 按能控性分解

8.1.1.1. 非奇异变换矩阵T的选取

8.1.1.2. 例子

8.1.2. 按能观性分解

8.1.2.1. 非奇异变换矩阵T的选取

8.1.2.2. 例子

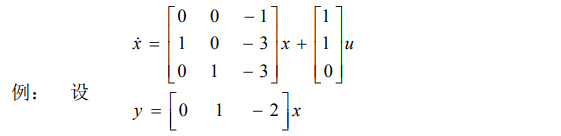
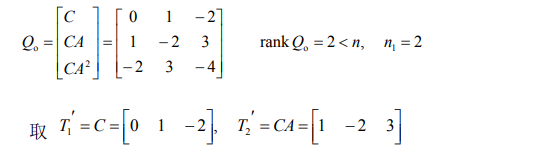
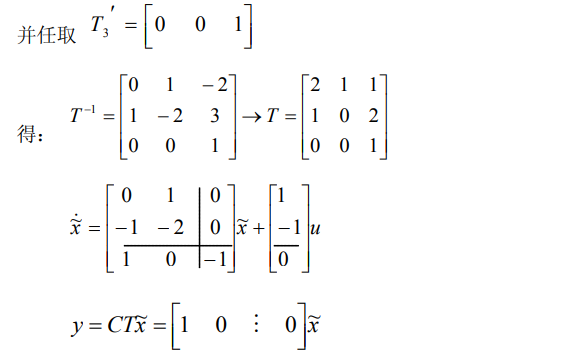
8.1.3. 规范分解定理

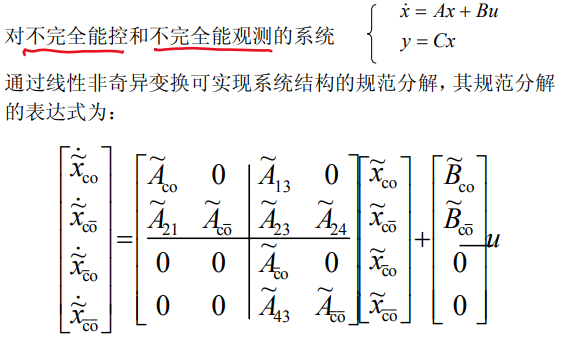
结论

8.1.3.1. 传递函数矩阵的最小多项式表示形式

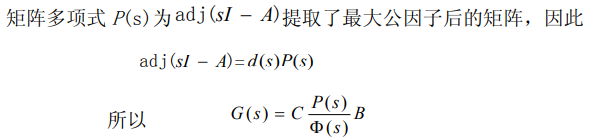
例子

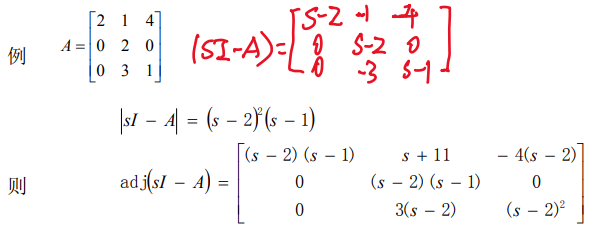
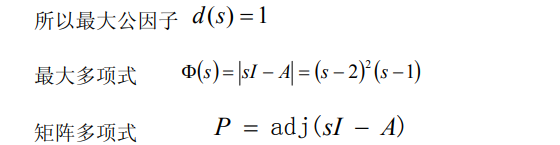
8.1.4. 传递函数中零、极点相消定理

8.1.4.1. 例子