LOAM: Lidar Odometry and Mapping in Real-time

摘要
主要思想,通过两个算法来同时优化大量变量,其中一个是作为高频输出的里程计,另一个是以更低的固定频率运行的后端优化。结合这两种算法,该方法可以实现实时分析。该方法已通过大量的实验和KITTI测程基准进行了评价。结果表明,该方法可以达到最先进的离线批处理方法的水平
- 由于此方法是为了在测程估计中最小化漂移,所以目前不涉及
Loop Closure
去畸变
如果扫描运动相对缓慢(扫描周期长),运动失真会很严重。
文献[13]提出了一种两步法来去除激光雷达的畸变
- 使用速度来矫正(其他传感器提供速度,或者使用ICP等算法来估计速度)
Barfoot等人使用的一种方法是从激光强度返回中创建视觉目标,并在两帧图像之间匹配视觉上不同的特征[17],以恢复地面车辆的运动[18]~[21]。其中,文献[18,19]把车辆的运动建模为恒速度模型。
[18]~[21]的方法涉及灰度图像的视觉特征,需要密集的点云,本文提出的方法在笛卡尔空间中提取和匹配几何特征,对云密度要求较低
符号约定
作为本文的一个惯例,我们使用右大写字母来表示坐标系统,使用右下标\(k,k\in Z^+\)来表示扫描,其中\(\mathcal{P}_k\)表示在第k次扫描的点云。
定义两个坐标系描述如下
- 激光雷达坐标系\(L\),原点是激光雷达中心,x轴指向左侧,y轴指向上,z轴指向前方。对于此坐标系下的一个点\(i,i \in \mathcal{P}_k\),可以记为\(X_{(k,i)}^L\)
- 世界坐标系\(W\),原点是激光雷达的初始位姿,此坐标系下的点,记为\(X_{(k,i)}^W\)
系统概述
硬件
采用180度视野范围,0.25度分辨率,40线的激光雷达UTM-30LX

软件系统
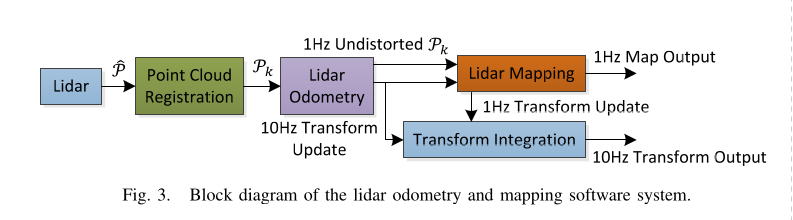
- \(\hat{\mathcal{P}}\)作为一帧扫描所得到的点,在每一次扫描中,\(\hat{\mathcal{P}}\)被配准到激光雷达坐标系中
- 然后\(P_k\)使用两种算法来处理:
- 首先是激光里程计,计算两帧扫描来估计激光雷达的相对运动,估计得到的运动反过来矫正\(\mathcal{P}_k\)的畸变,这个算法运行的频率为10Hz。
- 里程计的输出作为建图模块的输入,以1Hz的频率将去畸变后的点云进行匹配和配准到地图上。最后,将两个算法的结果进行整合,以10Hz输出位姿变换矩阵。
激光里程计
特征提取
选取点云中边缘上的点以及平面上的点。
- i: 点云\(\mathcal{P}_k\)中的点
- S: 同一帧扫描中与点i连续的点集
定义如下函数来评估某个点的平滑度:
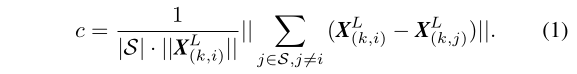
- 根据计算得到的\(c\)值进行排序,具有最大c值的特征点被选中,作为边缘点
- 具有最小c值的点也选中,作为平面点
为了将特征点均匀地分布在环境中,我们将一次扫描分成四个子区域,每个子区域能最多提供2个边缘点和4个平面点。只有当点i的c值比阈值大或者小的时候,才会被考虑作为边缘点或者平面点,另外还要求选择的特征点不超过子区域最大值。
在选择特征点时,我们希望避免重复选取:
- 某个已选中的特征点的附近点
- 与激光束大致平行的平面上的点(如图4(a))
这些点通常认为是不可靠的,同时,我们要避免在被遮挡的区域边界上的点,如下图4(b),点A是激光雷达云中的边缘点,因为它连接的表面(虚线段)被另一个物体阻塞了。然而,如果激光雷达移动到另一个视点,被遮挡的区域就会发生变化,成为可观测的。
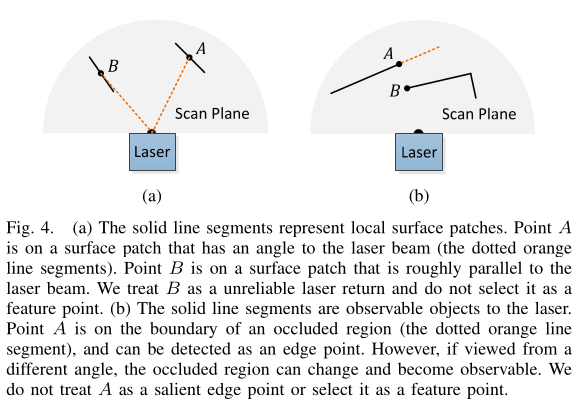
如何处理:
为了避免前面提到的点被选择,使用点集\(\mathcal{S}\)进行判断:
- 点集\(\mathcal{S}\)不形成与激光束平行的平面
- 点集\(\mathcal{S}\)中没有任何点是(由于激光束方向的gap导致)与点i不连续的,并且比点i更加靠近激光雷达的
!!!则点i才有可能被选中!!!
小结
综上所述,特征点的选取:以最大c值为起点来选择边缘点,以c值最小值为起点来选择平面点,
- 选择的边缘点或平面点不超过子区域的最大值
- 候选点i的附近点没有被选中
- 候选点i所在的 局部平面 不能与激光束方向平行,或者是被遮挡区域的边界点
如下图5所示
- 黄色:边缘点
- 红色:平面点

查找特征点关联
- \(t_k\):第k帧扫描的起始时间
- \(\bar{\mathcal{P}}_k\):第k帧扫描重投影到第k+1帧扫描起始时刻的点云
在每一帧扫描的结束时,在该帧扫描得到的点云\(\mathcal{P}_k\)被重投影到时间戳为\(t_{k+1}\),如图6所示。在接下来的\(t_{k+1}\)时刻的扫描中,\(\bar{\mathcal{P}}_k\)与\(t_{k+1}\)新扫描点云\(\mathcal{P}_{k+1}\)一起用来估计激光雷达的运动。
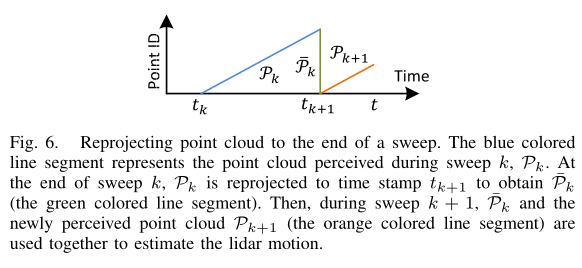
假设\(\bar{\mathcal{P}}_k\)和\(\mathcal{P}_{k+1}\)都可用,然后开始寻找两帧点云之间的关联。
对于点云\(\mathcal{P}_{k+1}\),先选出边缘点和平面点。
- \(\mathcal{E}_{k+1}\):边缘点集合
- \(\mathcal{H}_{k+1}\):平面点集合
注意,在扫描\(k+1\)开始时,\(\mathcal{P}_{k+1}\)是一个空的点集,在扫描过程中,随着接收到更多的点,该点数会增长。激光里程计连续地估计扫描中的6自由度的运动,同时\(\mathcal{P}_{k+1}\)点数增加。
在每次迭代中,使用当前的里程计位姿估计,将\(\mathcal{E}_{k+1}\)和\(\mathcal{H}_{k+1}\)投影到当前帧的扫描起始时刻,分别得到\(\bar{\mathcal{E}}_{k+1}\)和\(\bar{\mathcal{H}}_{k+1}\)
对于\(\bar{\mathcal{E}}_{k+1}\)和\(\bar{\mathcal{H}}_{k+1}\)中的每一个点,我们准备从点云\(\bar{\mathcal{P}}_k\)中选择最近邻的点,注意:为了快速查找,点云\(\bar{\mathcal{P}}_k\)以3D-KD-tree形式来储存
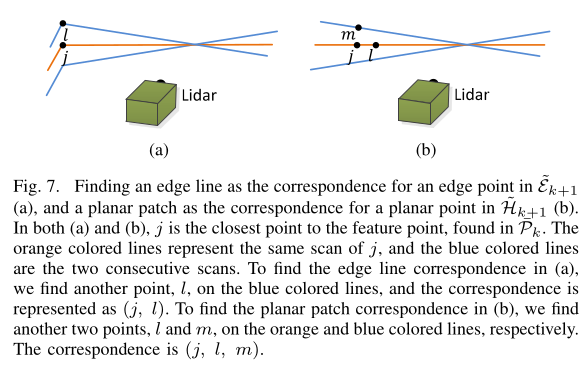
边缘线点的关联
图7(a)表示了寻找与边缘点对应的边缘线的过程,假设:
- \(i\)是\(\bar{\mathcal{E}}_{k+1}\)中的点
- \(j\)是在\(\bar{\mathcal{P}}_k\)中与点\(i\)最近邻的点(图中的橙色线上的点)
- \(l\)是两个连续线束扫描中与点\(i\)最近邻的点(图中的上下两条蓝色线束)
- 那么\((j,l)\)表达了一条关于点\(i\)的边缘线
边缘线使用两个点来表示:
\((j,l)\)形成了点i的关联,为了确认点\(j\)和\(l\)都是边缘点,我们基于平滑度计算公式来对局部平面的平滑度进行检查。在这里,特别要求\(j\)和\(l\)是来自不同线束的扫描,原因是考虑到一线束的扫描中,对于同一个边缘线不能超过1个点。(只有一个例外,即边缘线在扫描平面上,在这种情况下,边缘线会退化为扫描平面上的一条直线,线上的特征点不应该被首先提取)
平面点的关联
图7(b)展示了查找与平面点\(i\)相关联的平面块的过程,假设
- \(i\):\(\bar{\mathcal{H}}_{k+1}\)中的点
- \(j\):在\(\bar{\mathcal{P}}_{k}\)中关于点\(i\)的最近邻点
- \(l\):在与点\(j\)的同一线圈扫描中,另一个与点\(i\)的最近邻点
- \(m\):在与点\(j\)的相邻两线圈扫描中,与点\(i\)的最近邻点
平面块(planer patch)使用3个点来表示:
- 在\(\bar{\mathcal{P}}_{k}\)中查找关于点\(i\)的最近邻点,记为\(j\)
- 在与点\(j\)的同一线圈中,另一个与\(i\)最近邻的点,记为\(l\)
- 在与点\(j\)的相邻两线圈扫描中,找到与点\(i\)的最近邻的点,记为\(m\)
这样,保证了这3个点\((j,l,m)\)不共线,为了确定\((j,l,m)\)是否都是平面点,再次使用公式一来检查对应的平滑度。
特征距离表达式
这个特征距离作为目标函数的一部分,通过最小化目标函数,来求解出激光雷达的运动。
根据找到的特征点的对应关系,计算从特征点到对应特征关联的距离:
边缘线特征距离
对于每一个在边缘集合\(\bar{\mathcal{E}}_{k+1}\)中的点,如果\((j,l)\)是对应该点的边缘线,那么就可以计算特征距离:
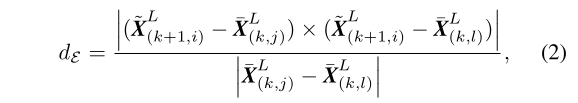
其中,
- \(\bar{X}_{k+1,i}^L\)是点\(i\)在{L}中的坐标
- \(\bar{X}_{k,j}^L\)是点\(j\)在{L}中的坐标
- \(\bar{X}_{k,l}^L\)是点\(l\)在{L}中的坐标
公式原理: 叉乘计算出平行四边形面积 在除以长度,可以得到点到线的垂线距离
平面点特征距离
对于在平面集合\(\bar{H}_{k+1}\)中的点\(i\),如果\((j,l,m)\)是对应的平面块,那么那么点\(i\)到平面块\((j,l,m)\)的距离为:
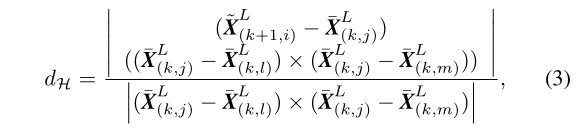
其中,
- \(\bar{X}_{k,m}^L\)是点\(m\)在{L}中的坐标
运动估计
在扫描过程中,假设激光雷达的运动以恒定的角速度和恒定的线速度进行(匀速模型)。
这种假设允许我们在一帧扫描中(a sweep)对每一个在不同时间接收到的点对应的激光雷达位姿进行线性插值得到。
假设:
- \(t\): 当前时刻时间戳
- \(t_{k+1}\): 在第k+1帧扫描的起始时刻
- \(T_{k+1}^L\): 在时间段\([t_{k+1},t]\)之间的激光雷达位姿变换\(T_{k+1}^L=[t_x,t_y,t_z,\theta_x,\theta_y,\theta_z]^T\)(旋转部分遵循右手系)
给定一个在\(\mathcal{P}_{k+1}\)中的点\(i\)
- \(t_i\)为接收到点\(i\)的对应时刻\((t_i \in [t_{k+1},t])\)
- \(T_{(k+1,i)}^L\)为时间段\([t_{k+1},t_i]\)之间的激光雷达位姿变换 ===> 从\(t_i\)时刻激光雷达坐标系转换到\(t_{k+1}\)时刻的激光雷达坐标系的变换
那么,\(T_{(k+1,i)}^L\)可以通过对\(T_{k+1}^L\)进行线性差值得到:
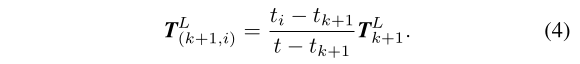
回想一下:
- \(\mathcal{E}_{k+1}\)和\(\mathcal{H}_{k+1}\)分别是从\(\mathcal{P}_{k+1}\)提取出来的边缘点和平面点集合
- \(\tilde{\mathcal{E}}_{k+1}\)和\(\tilde{\mathcal{H}}_{k+1}\)是将上面的点集重投影回在第\(k+1\)帧扫描的起始时刻的点集
为了求解激光雷达的运动,我们需要建立
- \(\mathcal{E}_{k+1}\)和\(\tilde{\mathcal{E}}_{k+1}\)
- \(\mathcal{P}_{k+1}\)和\(\tilde{\mathcal{H}}_{k+1}\)
之间的几何关系。
使用公式(4)的变换,可以推导得到上述关系:
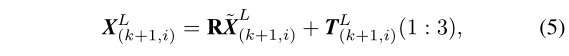
其中,
- \(X_{(k+1,i)}^L\)是点\(i\)投影到\(t_{k+1}\)时刻下的激光雷达坐标系的坐标
- \(T_{(k+1,i)}^L(1:3)\)表示从\(t_i\)时刻激光雷达坐标系转换到\(t_{k+1}\)时刻的激光雷达坐标系的平移量变换
- \(R\)是使用罗德里格斯公式得到的旋转矩阵
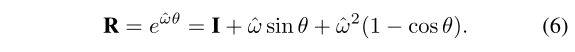
上式中的\(\theta\)为,表示旋转的量:
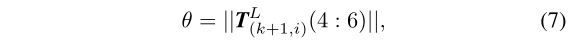
\(w\)是单位向量,表示旋转的方向,\(\hat{w}\)是关于向量\(w\)的反对称矩阵:
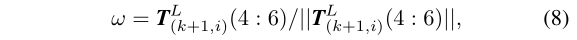
回想一下:公式(2),(3)计算了\(\tilde{\mathcal{E}}_{k+1}\)和\(\tilde{\mathcal{H}}_{k+1}\)中的点与其对应的特征关联之间的距离,
结合公式(2)和(4~8),我们可以推导出集合\(\mathcal{E}_{k+1}\)中的边缘点和其对应的特征关联之间的几何关系:
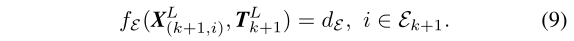
同样的,结合公式(3)和(4~8),有:
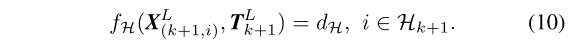
最后,通过LM算法来求解激光雷达的运动:
对于在\(\mathcal{E}_{k+1}\)和\(\mathcal{H}_{k+1}\)中的每个点,都可生成如同式(9)和(10)的方程,通过遍历,可以得到一个非线性函数:
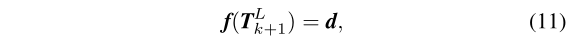
其中,
- \(f()\)中的每一行与一个特征点相关联
- \(d\)包含了对应的特征关联距离
然后计算矩阵\(f()\)关于\(T_{k+1}^L\)的雅克比矩阵,即
\[ J=\frac{\partial f}{\partial T_{k+1}^L} \]
然后,式(11)可以通过以最小化\(d\)为目标,使用非线性迭代来求解:
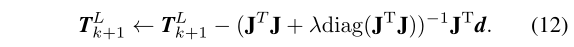
(QPC: add)那么,每次迭代的增量方程应该是:
\[ (J^TJ+\lambda)dx=J^Td \]
其中
- \(\lambda\)是LM算法的参数
小结
激光里程计的算法,总结如下图

建图(LIDAR MAPPING)
建图算法以低频率运行,每一圈扫描执行一次。在第k+1圈扫描的结束时刻,里程计模块生成去畸变后的点云\(\bar{P}_{k+1}\),同时还有激光雷达的相对位姿变换\(T_{k+1}^L\)。
建图部分将去畸变后的点云\(\bar{P}_{k+1}\)配准到世界坐标系\({W}\)中,如下图8所示
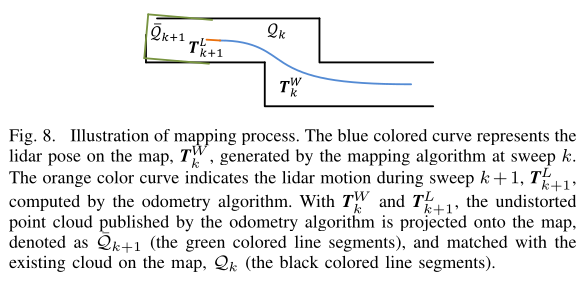
- \(Q_k\): 地图上的点云,是前k帧扫描的累积形成的
- \(T_k^W\): 在第k帧扫描结束时刻(也是\(t_{k+1}\)),雷达在点云地图上的位姿
未完待续