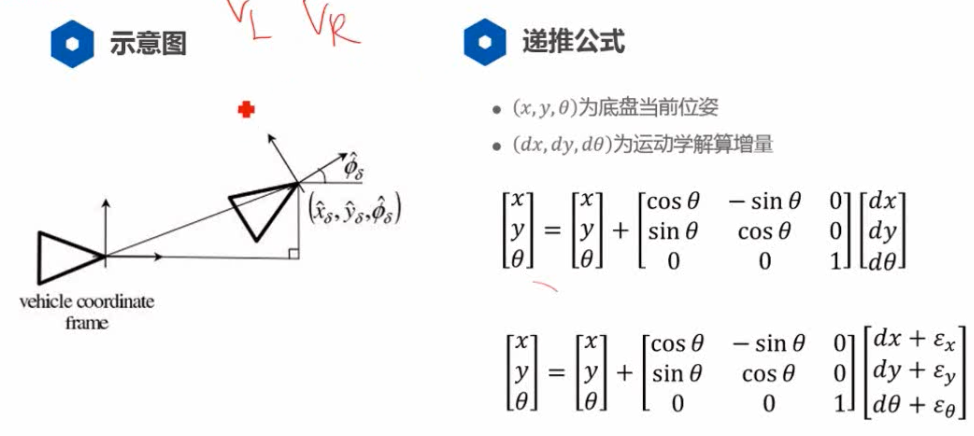
两轮差速底盘的三种航迹推算模型
差速底盘分析
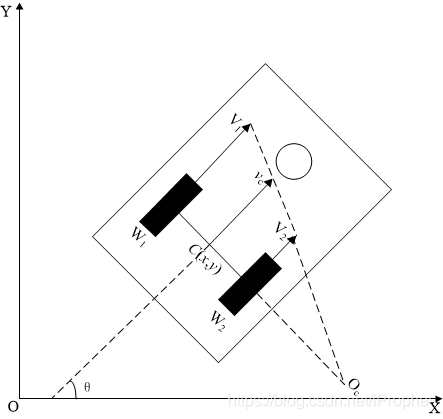

航迹推算
- 机器人坐标系为 x轴为前进方向,z轴朝上的右手坐标系
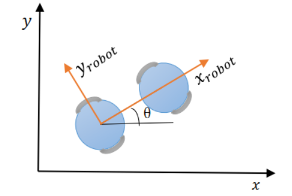
(1)直线假设<概率机器人>
切线模型最为简单,是ROS中采用的运动模型。它假设机器人在原来的方向上,沿着直线运动,再转角度
假设
- 机器人沿着当前方向前进
- 到达后,再执行旋转操作
因此,有:
\[ \begin{cases}x_{t+\Delta t}=x_{t}+\Delta x\cdot \cos \varphi _{t}\\ y_{t+\Delta t}=y_{t}+\Delta x\cdot \sin \varphi _{t}\\ \varphi _{t+\Delta t}=\varphi _{t}+\Delta \varphi \end{cases} \]
(2)割线模型
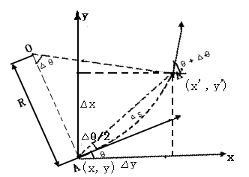
如图所示的直角坐标系,机器人从\(A(x,y,\theta)\)出发,经过\(\Delta t\)到达\(A'(x',y',\theta')\),其中,x和y分别为世界坐标系的坐标,\(\theta\)是机器人坐标系x轴与世界坐标系横轴的夹角,逆时针为正。
设:
- \((\Delta x,\Delta y,\Delta \phi)\)是相对于世界坐标系的增量
- \(\Delta S\)表示A点到A'点的弧长
因此,\(\Delta x,\Delta y\)推导如下:
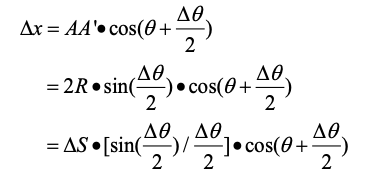
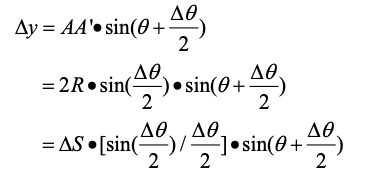
其中,\(AA'\)表示A点到A'点的直线距离
并且,
\[ \sin(\frac{\Delta \theta}{2})/\frac{\Delta \theta}{2} \approx 0 \]
因此,有:
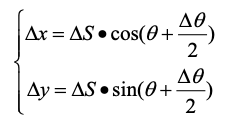
这个模型的关键在于,假设时间间隔\(\Delta t\)很短,那么\(AA'\)近似等于\(\Delta S\),即用圆的割线长度来近似圆弧长度,最终,有:
\[ \begin{aligned} x' &=x+\Delta x = x+ AA' \cos(\theta + \frac{\Delta \theta}{2}) \\ &=x+\Delta S \cos(\theta + \frac{\Delta \theta}{2}) \end{aligned} \]
\[ \begin{aligned} y' &=y+\Delta y = y+ AA' \sin(\theta + \frac{\Delta \theta}{2}) \\ &=y+\Delta S \sin(\theta + \frac{\Delta \theta}{2}) \end{aligned} \]
割线模型的直观解释
可以理解为:假设机器人先转一半角度\(\frac{1}{2}\Delta \phi\),然后沿着此方向运动,最后再转剩下的一半角度。
(3)圆弧模型
假设走的是真真的弧线,具体表达式是通过积分得到的,如下:
\[ \begin{aligned} \Delta x &= v_{t} \int_{t}^{t+\Delta t} \cos[\theta_{t}+(T-t)\omega]dT \\ &=\frac{v_t}{\omega}[\sin(\theta_t+\Delta \theta)-\sin \theta_t] \\ &=\frac{\Delta S}{\Delta \theta}[\sin(\theta_t+\Delta \theta)-\sin \theta_t] \end{aligned} \]
\[ \begin{aligned} \Delta y &= v_{t} \int_{t}^{t+\Delta t} \sin[\theta_{t}+(T-t)\omega]dT \\ &=\frac{v_t}{\omega}[-\cos(\theta_t+\Delta \theta)+\cos \theta_t] \\ &=\frac{\Delta S}{\Delta \theta}[-\cos(\theta_t+\Delta \theta)+\cos \theta_t] \end{aligned} \]
\[ \begin{cases} x_{t+\Delta t}=x_t+\Delta x \\ y_{t+\Delta t}=y_t+\Delta y \\ \theta_{t+\Delta t}=\theta+\Delta \theta \end{cases} \]
全向轮底盘的航迹推算模型

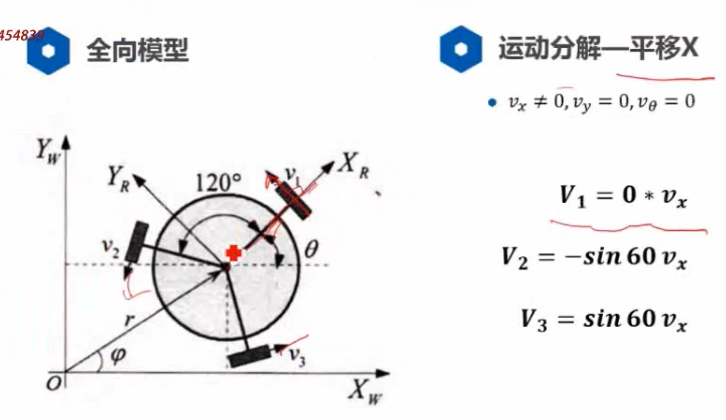
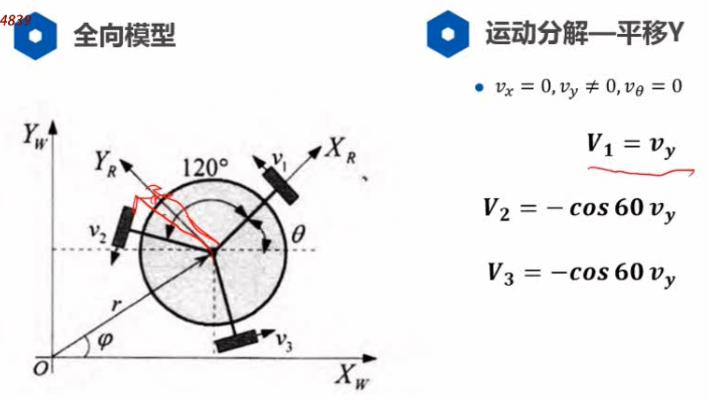
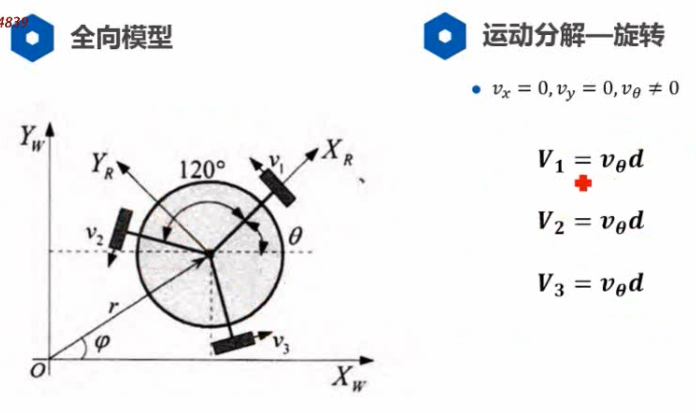
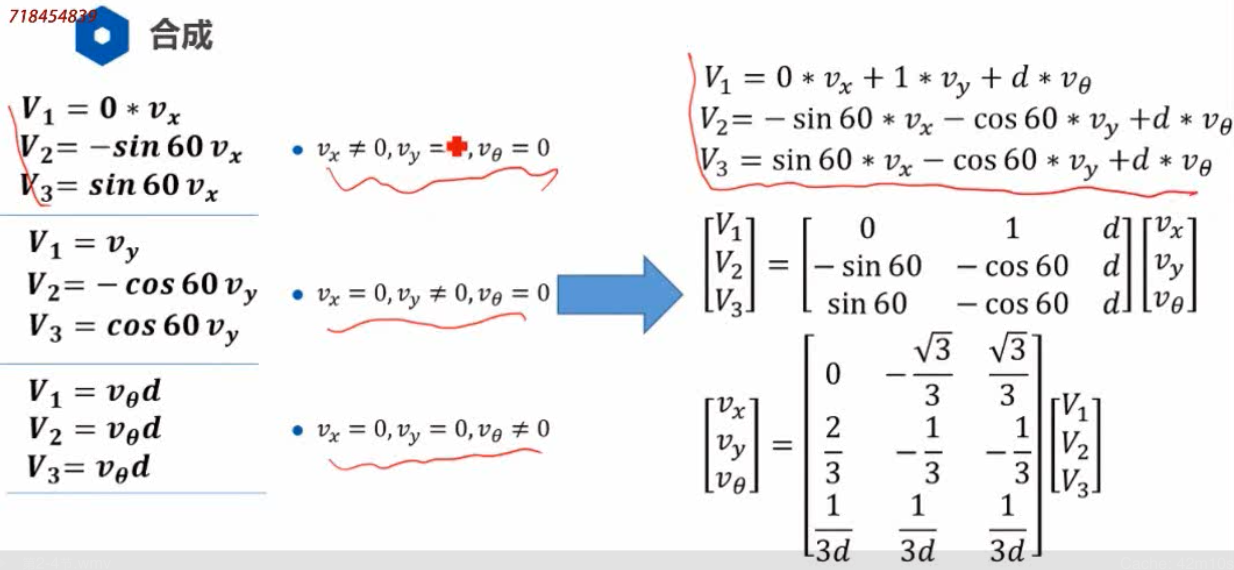
可以走任意方向,因此: