回环检测
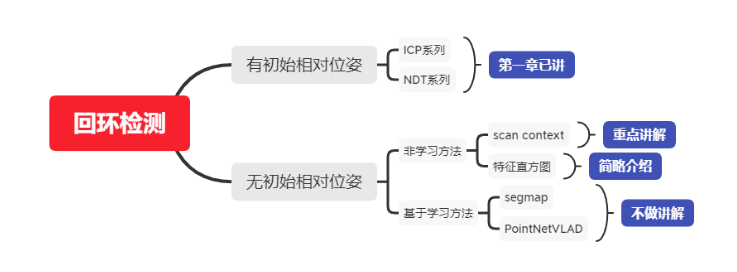
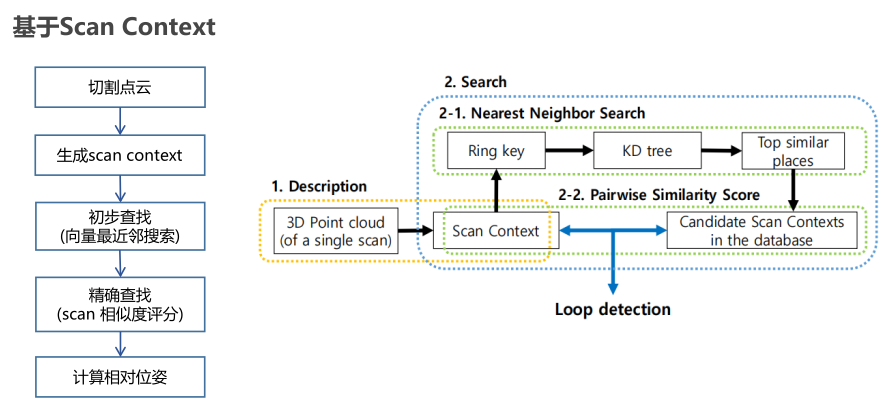
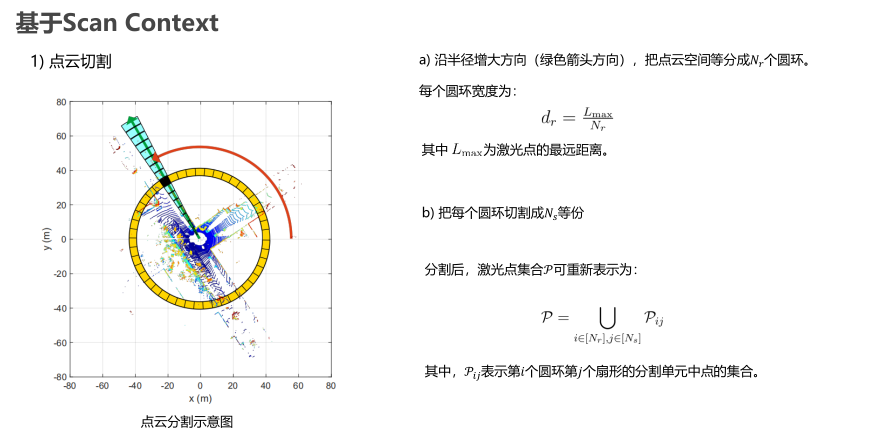
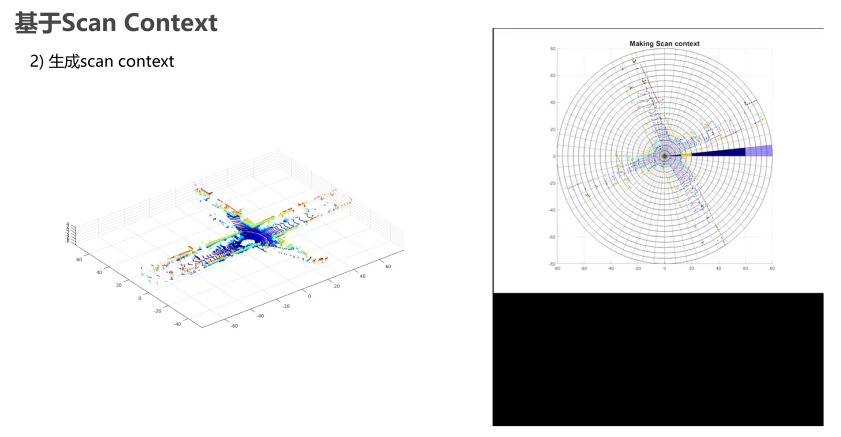
基于Scan-Context
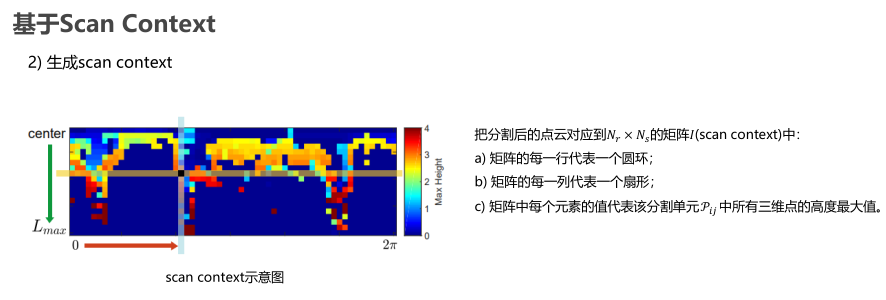
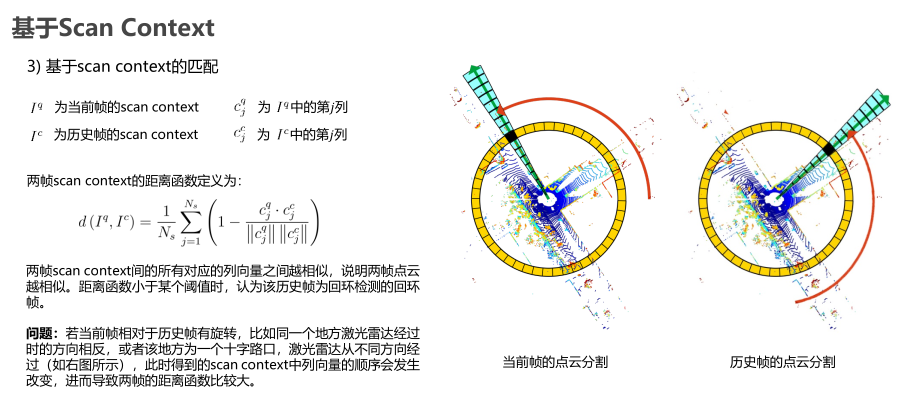
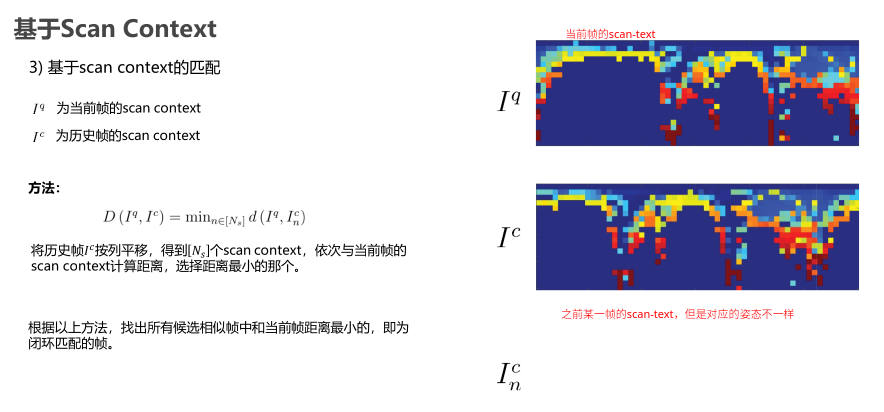

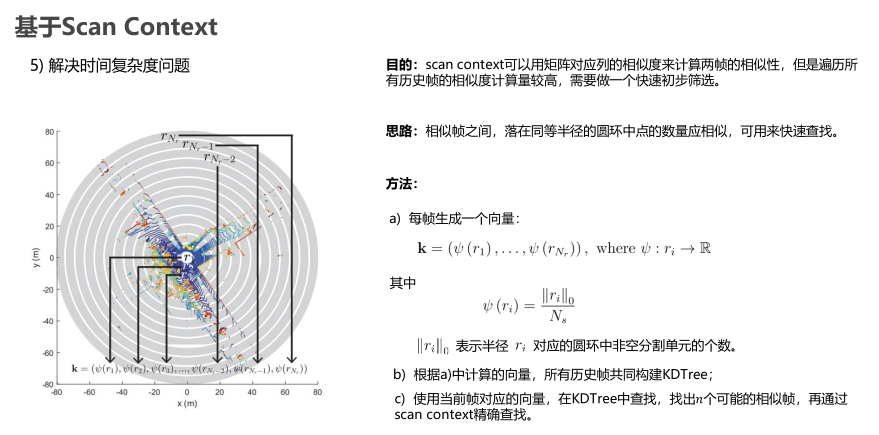
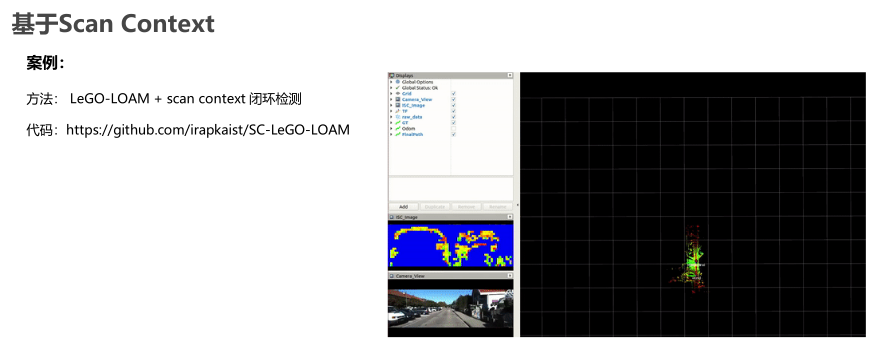
基于特征直方图

后端优化
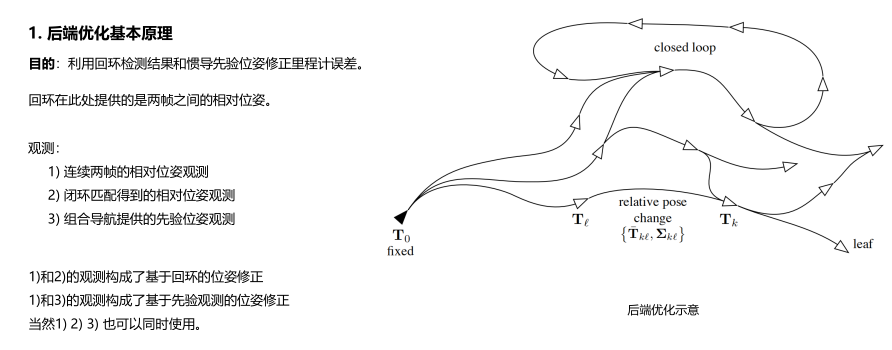
基础知识
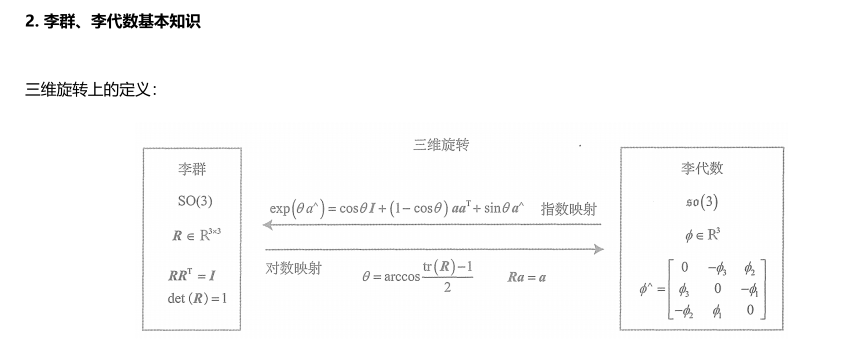
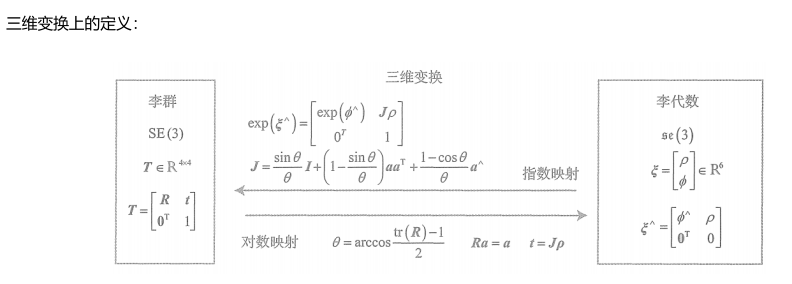


这里说的是:
假定对某个旋转\(R\),对应李代数为\(\phi\)。我们给它左乘一个微小旋转,记做\(\Delta R\),对应的李代数为\(\Delta \phi\),那么,在李群上,得到的结果是\(\Delta R\cdot R\),而在李代数上,根据BCH近似公式,即相加后对应的李代数为\(J_r{-1}(\phi)\Delta \phi+\phi\) \[ \exp(\Delta \phi^{\wedge})\exp(\phi^{\wedge})=\exp((J_r^{-1}(\phi)\Delta\phi+\phi)^\wedge) \]

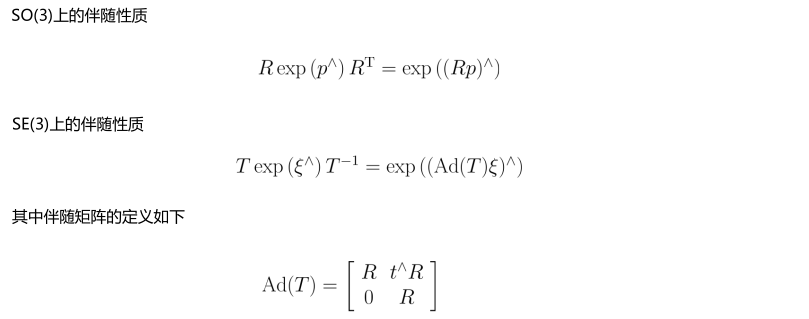
伴随矩阵通常用于变量顺序转换,用于公式化简
基于回环的修正
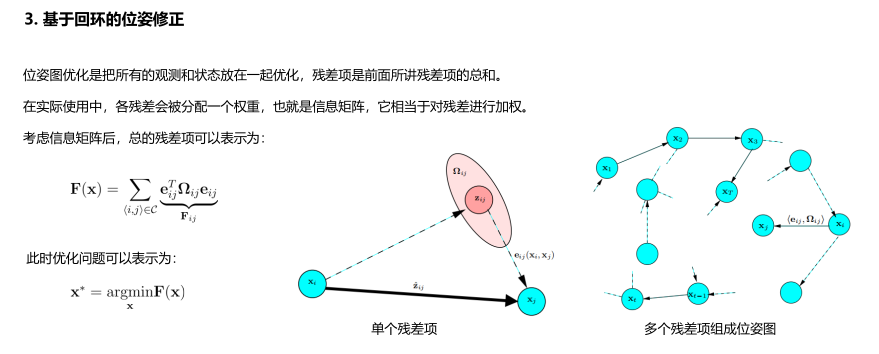

下面进行公式推导:
假设如下:
- 第i帧位姿估计\(T_i\)
- 第j帧位姿估计\(T_j\)
- 某个绝对观测:第j帧到第i帧的变换\(T_{mij}^{-1}=T_{mji}=T_{mi}^{-1}T_{mj}\)
现在需要构建残差:
- 假设位姿采用6维se3描述
- 第i帧位姿估计\(T_i=\exp(\xi_{i}^{\wedge}) ===> \xi_i=\ln(\exp(\xi_i^{\wedge}))^{\vee}\)
- 第j帧位姿估计\(T_j=\exp(\xi_{j}^{\wedge}) ===> \xi_j=\ln(\exp(\xi_j^{\wedge}))^{\vee}\)
即 残差=观测-估计
\[ \begin{aligned} e_{ij}&=\xi_{mea}-\xi_{ji} \\ e_{ij}&=ln(T_{mij}^{-1}T_i^{-1}T_j)^{\vee} \end{aligned} \]
问题来了,优化通常采用迭代法,如高斯牛顿,LM等,均需要求解雅克比矩阵,而李代数求解导需要借助“扰动”
如采用左乘雅克比
\[ \begin{aligned} \widehat{e_{ij}}&=\ln(T_{mij}^{-1} \left \{ \exp((\delta\xi_i)^{\wedge})T_i \right \}^{-1} \left \{ \exp((\delta\xi_j)^{\wedge})T_j \right \} )^{\vee} \\ &=\ln(T_{mij}^{-1} \left \{ T_i^{-1}\exp((-\delta\xi_i)^{\wedge}) \exp((\delta\xi_j)^{\wedge})T_j \right \} )^{\vee} \\ \end{aligned} \]
下面的化简用到了上面ppt的近似公式、伴随性质

.png)
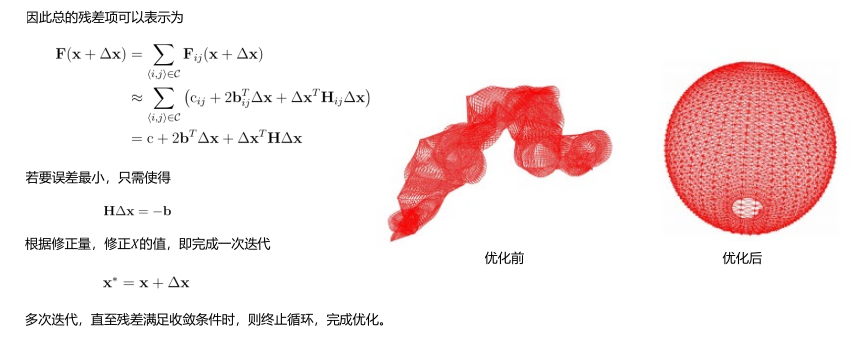
上述内容跟《视觉SLAM14讲》的位姿图优化是一致的。
基于先验的修正

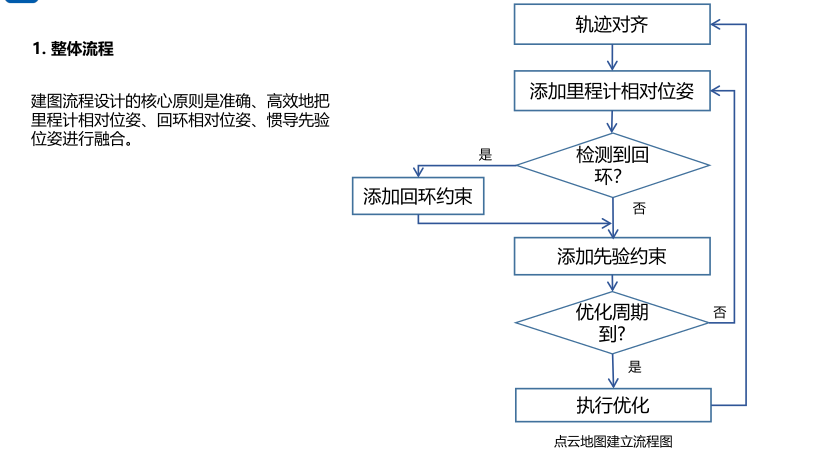
建图
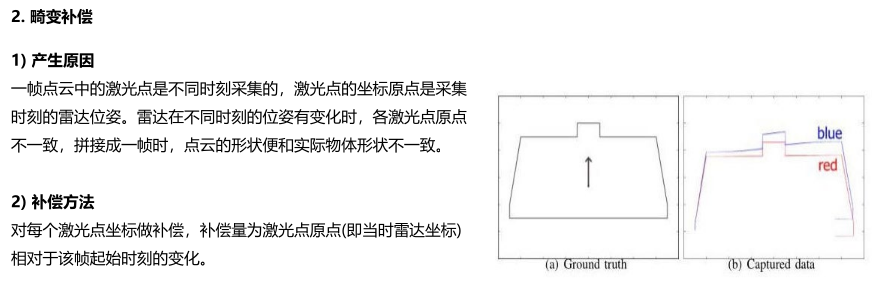
激光点云畸变

定位
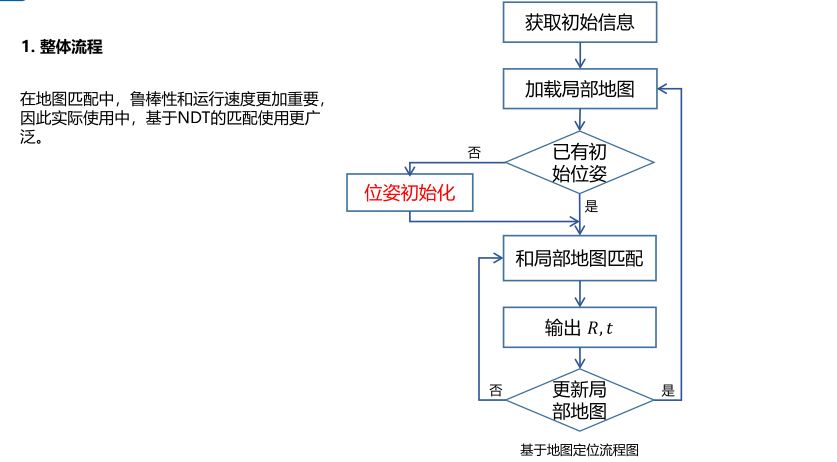
基于地图定位

作业
