A Robust and Easy to Implement Method for IMU Calibration without External Equipments

介绍
一个理想的imu,其三轴应该是与三个正交的敏感轴重合的,并且具有确定的尺度因子,但不幸的是,低成本的mems imu通常会受到non accurate scaling,sensor axis misalignments,cross-axis sensitivities以及bias的影响。
IMU标定,其实就是对上述参数的辨识过程。
传感器误差模型
对于理想的imu,加速度计和陀螺仪的三轴是重合、正交的。每个加速度计只测量沿着该轴方向的加速度,而陀螺仪则测量围绕同一轴的角速度。
然而,实际使用中的imu,由于装配等原因,两个三轴坐标系并未对准,从而形成两个非正交的坐标系。
另外,即使是单个传感器(加速度计/陀螺仪)也不是完美的,因为用于转换实际物理量的数字比例因子对于同一传感器的不同实例对象是不同的,厂商仅提供默认的标称比例因子。
其次,还有bias的影响。
下面是一些坐标系的定义:
- AF:加速度计坐标系(非正交)
- GF:陀螺仪坐标系(非正交)
- AOF:与AF坐标系关联的正交坐标系
- 其中,AOF的x轴与AF的重合
- AOF的y轴处于AF坐标系中x轴与y轴所张成的平面中
- GOF:类似同理
- BF:载体坐标系(正交)
对于小角度导致的非正交的情况,在AF或GF坐标系中的测量值\(s^{\mathcal{S}}\)可以使用如下变换,转换到正交的载体坐标系下:
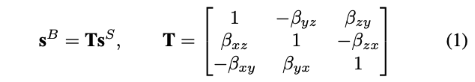
其中,
- \(s^{\mathcal{B}},s^{\mathcal{S}}\)可以是加速度或者角速度,分别在载体坐标系和加速度计(陀螺仪)坐标系的表示
- \(\beta_{ij}\)表示加速度计的第i轴绕载体坐标系的第j轴的旋转,如下图2
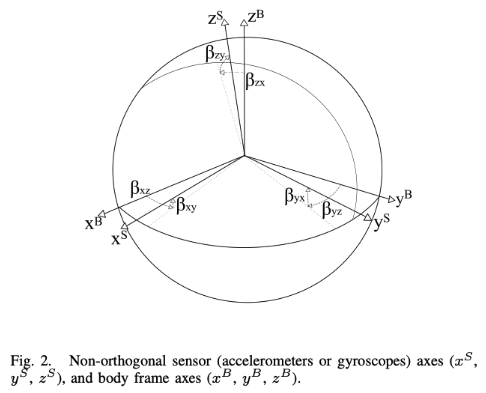
关于矩阵T的直观解释,这个矩阵按列来看比较清晰,以第一列为例子,\([1,\beta_{xz},-\beta_{xy}]\), - 1可以理解成\(\beta{xx}\),其意义是表示加速度计坐标系的x轴由于没对齐,绕载体坐标系x轴旋转所产生的误差对 载体坐标系x轴分量造成的影响,由于没有影响,所以是1 - \(\beta_{xz}\),表示加速度计坐标系的x轴由于没对齐,绕载体坐标系z轴旋转所产生的误差对 载体坐标系y轴分量造成的影响。 - \(-\beta_{xy}\),表示加速度计坐标系的x轴由于没对齐,绕载体坐标系y轴旋转所产生的误差对 载体坐标系z轴分量造成的影响。(图中绕y轴顺时针转了,而正方向是逆时针,所以加负号)
另外,载体坐标系BF和加速度关联正交坐标系AOF由一个旋转关联起来了。
提出的方法中,假设载体坐标系BF与加速度计关联正交坐标系AOF一致:此时,\(\beta_{xz},\beta_{xy},\beta_{yx}\)变成0,因此,等式1变成:
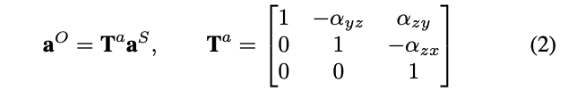
其中,使用\(\alpha\)来替换\(\beta\)以表示更为通用的情况,对于加速度计,则有\(a^{\mathcal{O}}\)和\(a^{\mathcal{S}}\)分别表示在AOF和AF坐标系的表示。
对于陀螺仪,同理有:
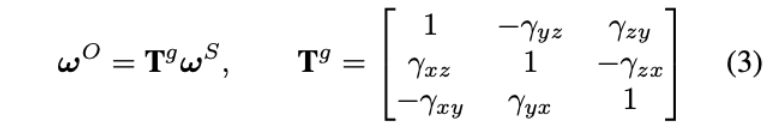
其中,
- \(\omega^{\mathcal{O}}\)表示在AOF坐标系的角速度
- \(\omega^{\mathcal{S}}\)表示在GF坐标系的角速度
加速度计和陀螺仪的刻度因子矩阵如下:
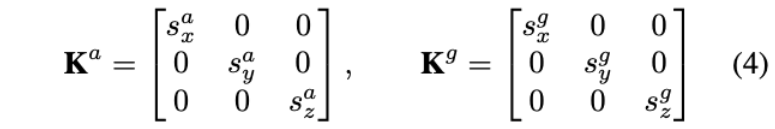
零偏(Bias)如下:
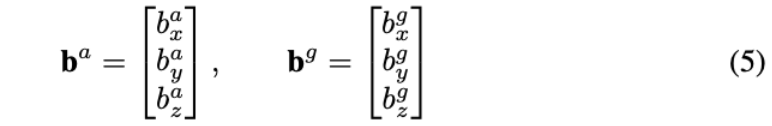
因此,进行误差补偿之后的输出值(矫正值)如下:
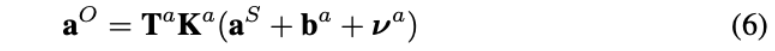
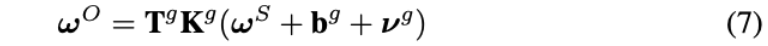
其中,
- \(\nu^{a}\)表示加速度计测量噪声
- \(\nu^{g}\)表示陀螺仪测量噪声
标定Framework
加速度计
为了标定加速度计,需要估计如下参数:
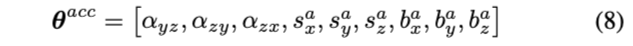
定义补偿模型函数如下:
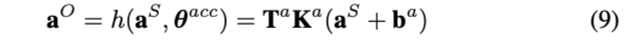
这里忽略了测量噪声。
定义cost funstion如下:
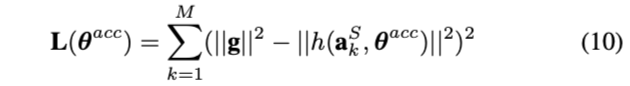
其中,
- \(||g||\)表示当地重力向量的模(可以查表得到)
与传统的多位置方案一样,我们平稳的旋转imu,一共M个方案。然后提取M个加速度计输出量\(a_k^{\mathcal{S}}\)(即非正交坐标系的测量值),然后将每个静态间隔时间中的加速度计读数求平均。
陀螺仪
为了标定陀螺仪,这里假设陀螺仪的bias为0,只需在适当的初始静止时间段内对静态陀螺仪信号进行平均即可
此外,由于我们需要使用加速度计作为已知的参考坐标系,因此我们使用上面标定得到的参数\(\theta^{acc}\)并且使用等式(9)来得到补偿输出值。(即矫正之后的imu输出值)
这里定义一个操作符\(\Psi\),操作为:取n个陀螺仪读数\(\omega_i^{\mathcal{S}}\) 和 初始第k-1时刻的重力矢量\(u_{a,k-1}\)(由上面标定后的加速度计得到) 作为输入,然后返回第k时刻的矫正后的输出值\(u_{g,k}\),使用了从[k-1,k]时间间隔内的gyro测量值进行计算。

\(\Psi\)可以使用任一种积分方法来得到k时刻的姿态。
因此,需要估计的参数如下:
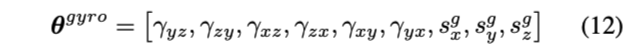
cost function如下:
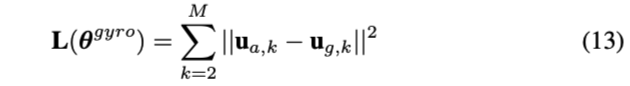
其中,
- \(M\)表示由多少段是静态的
- \(u_{a,k}\)表示在第k段静态时间内,加速度计补偿输出值的平均值
- \(u_{g,k}\)表示使用等式(11)在[k-1,k]间隔内进行积分得到载体的姿态,然后把初始重力(即k-1时刻下的加速度计补偿输出值的平均值)进行投影得到的投影值。
标定过程
如前文所述,提出的方法需要把imu移动到不同静态位置进行加速度计和陀螺仪的数据采集,如下图1报告了标定过程示意图。
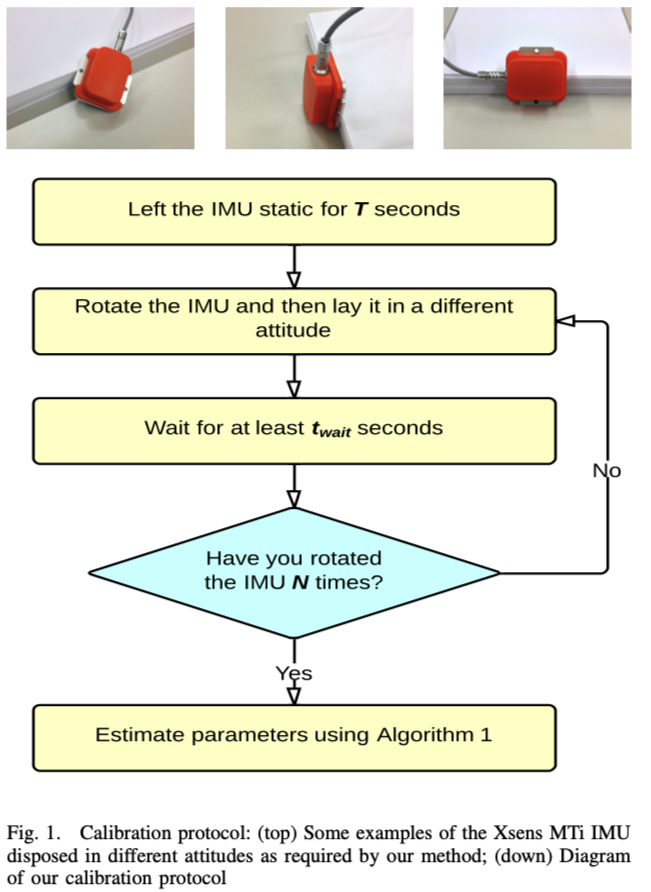
- 为了校准加速度计,我们使用静态间隔(单段就可以)
- 而对于陀螺仪校准,除了两个连续的静态间隔,还包括两个连续的静态间隔之间的
运动间隔(用来积分)
为了减少噪声的影响,需要对每个静态时间段的数据求平均, 同时也增加了静态时间段的长度下限(时间太短就不认为是静态的)
静态检测器
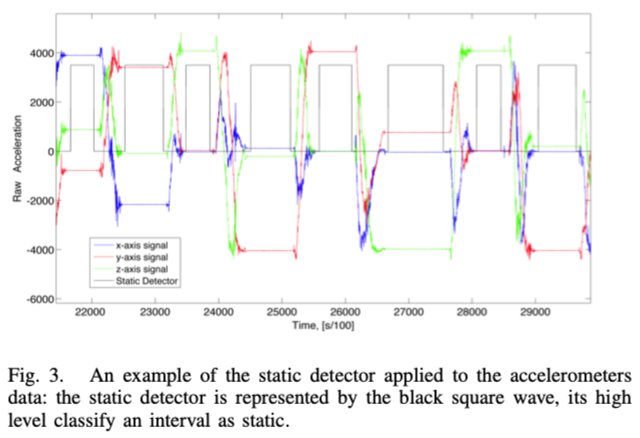
根据经验,基于带通滤波器的运算符(如[8]中使用的准静态检测器)在真实数据集上的性能较差:检测到的静态间隔通常包含一小部分运动。 此外,它们需要微调,因为它们取决于三个参数。提出的方法改为使用基于方差的静态检测器算子,该算子利用了上面介绍的静态间隔长度的下限
。。。。具体见原文描述
RK-4积分
式(15)是描述四元数运动学的微分方程:
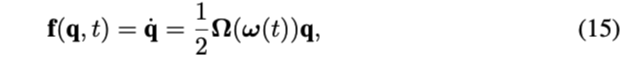
其中,
- \(\Omega(\omega)\)表示把三轴角速度变成反对称矩阵
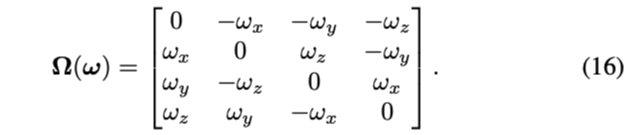
rk4积分算法如下:

Allan方差
最后,使用allan方差来表征陀螺仪的随机bias偏移,该方差用于测量连续区间平均值之间的差异方差
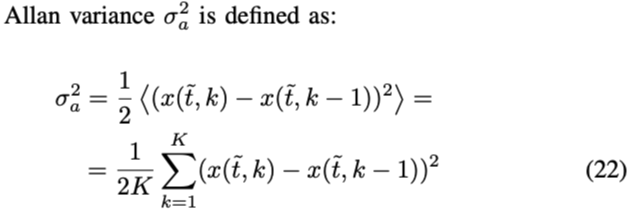
其中
- \(x(t,k)\)表示第k个静态间隔内平均值,跨度约为t秒
- K表示将考虑的总时间分割的间隔数
三个轴的Allan方差收敛到一个小值的时候代表了此时作为初始化周期\(T_{init}\)的是一个不错的选择(图4) ????????
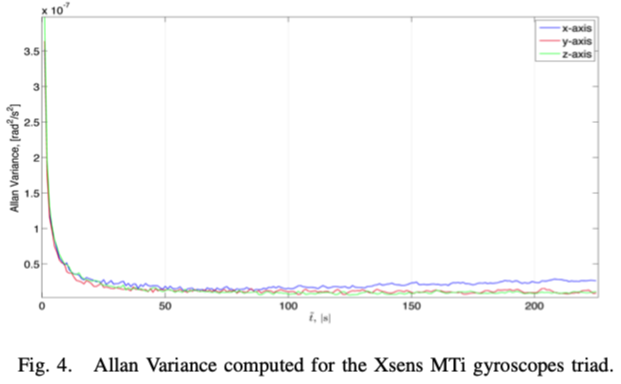
在此初始化期间,我们计算静态陀螺仪信号的平均值,以正确确定校准中使用的陀螺仪偏置
完整过程
为了避免在校准参数估算中产生不可观测性,必须至少收集九种不同的姿态[15]。根据我们的经验,需要更大数量的N的不同姿态才能获得更好的校准结果,同时保持减少每个静态间隔的持续时间,以便保留陀螺仪偏置的时间稳定性假设。
文章选取:
- 36<=N<=50
- 1s<=\(t_{wait}\)<=4s
初始化周期Tinit的持续时间由Allan方差分析给出
整体算法流程如下:
