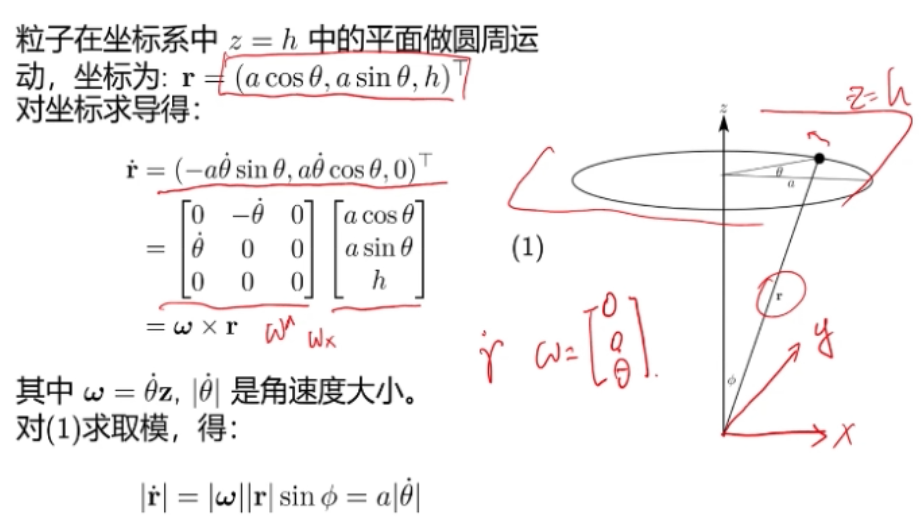
惯导解算

基础部分
旋转矩阵微分
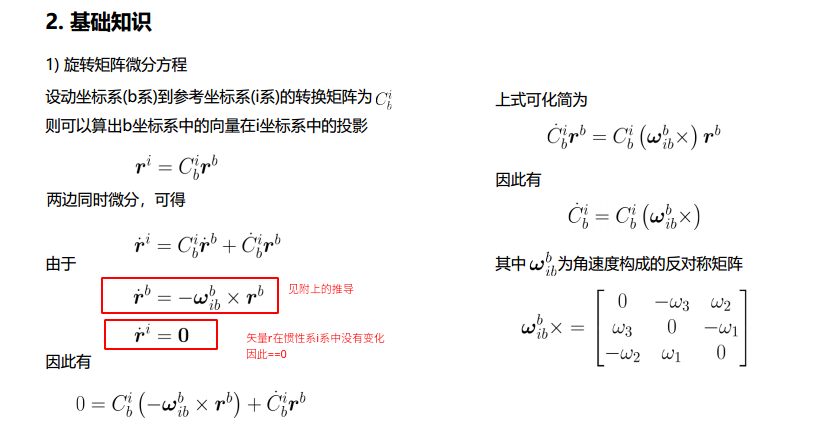
关于\(\dot{r}^{b}=-\omega_{ib}^{b} \times r^b\)的推导
其他求旋转矩阵微分的方法
考虑任意旋转矩阵\(R^TR=I\)
对于时变情况,有\(R^T(t) R(t)=I\)
对上式两边同时求导:
\[ \begin{aligned} \dot{R}^{T}R+R^T\dot{R}=0 \end{aligned} \]
整理,有:
\[ \begin{aligned} \dot{R}^{T}R&=-R^T\dot{R} \\ &=-(\dot{R}^{T}R)^T \end{aligned} \]
可以发现,\(\dot{R}^{T}R\)是一个反对称矩阵,因此可以使用一个三维向量的反对称矩阵来表示(实际上就是角速度)
\[ \dot{R}^{T}(t)R(t)=\phi(t)^\wedge \]
继续整理,有:
\[ \begin{aligned} \dot{R}^{T}(t)R(t)=\phi(t)^\wedge \\ \rightarrow \dot{R}^{T}(t)=\phi(t)^\wedge R(t)^T \\ \rightarrow \dot{R}(t)=(\phi(t)^\wedge R(t)^T)^T \\ \rightarrow \dot{R}(t)=R(t)\phi(t)^\wedge \end{aligned} \]
四元数及其微分



四元数微分-方法一


四元数微分-方法二(推荐)

具体可参见四元数微分
等效旋转矢量


旋转矩阵、四元数、等效旋转矢量之间的关系

姿态更新
基于旋转矩阵的更新

思想:把小周期内的角度增量看作是等效旋转矢量,然后进行姿态更新
基于四元数的更新
推导方法1

补充: \[ \begin{aligned} M_{w_{ib}^b}'= q_0 I + (\phi*)_2 &= \begin{bmatrix} q_0 & -\phi_x & -\phi_y & -\phi_z \\ \phi_x & q_0 & \phi_z & -\phi_y \\ \phi_y & -\phi_z & q_0 & \phi_x \\ \phi_z & \phi_y & -\phi_x & q_0 \end{bmatrix} \\ &= \begin{bmatrix} 0 & -\phi_x & -\phi_y & -\phi_z \\ \phi_x & 0 & \phi_z & -\phi_y \\ \phi_y & -\phi_z & 0 & \phi_x \\ \phi_z & \phi_y & -\phi_x & 0 \end{bmatrix} \end{aligned} \]
常系数微分方程求解
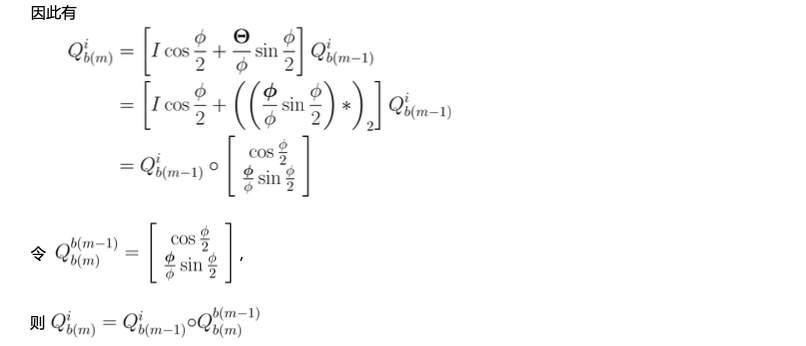
推导方法2


等效旋转矢量的计算(关键)
这里探讨的是 等效旋转矢量与角速度(角增量)之间的关系,实际上,等效旋转矢量\(\phi\)一般不等于角增量\(\Delta \theta\),当且近当载体做定轴旋转时(即等效旋转矢量与角速度矢量方向平行时),两者才相等。



解算部分
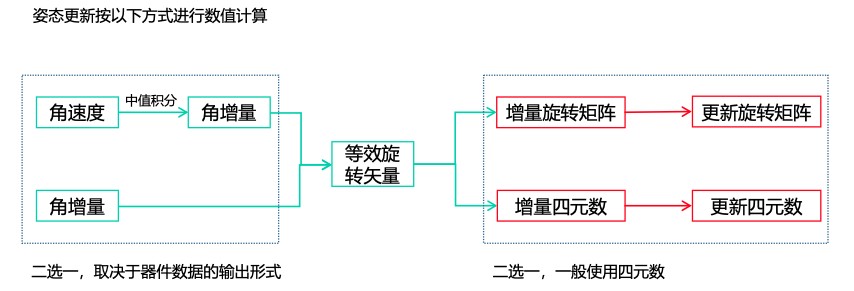


上图中圈起来的部分:
- \(C_{b(m)}^{n(m)}\) 表示\(t_m\)时刻下,载体相对于导航坐标系的姿态
- \(C_i^{n(m-1)}C_{b(m-1)}^i = C_{b(m-1)}^{n(m-1)}\) 表示\(t_{m-1}\)时刻下,载体相对于导航坐标系的姿态
- \(C_{b(m)}^{b(m-1)}=\exp([\phi_{ib(m)}^b]\times)\) 表示以i系作为参考基准,b系从\(t_{m-1}\)到\(t_m\)时刻的旋转变化,此量可由载体陀螺仪角速度\(\omega_{ib}^b\)确定
- \(\phi_{ib(m)}^b=(\Delta \theta_1+\Delta \theta_2)+\frac{2}{3}\Delta \theta_1 \times \Delta \theta_2\) 这是误差补偿项,用以补偿 等效旋转矢量与陀螺仪得到的角度增量之间的误差(不可交换误差),采用二子样圆锥误差补偿算法。(单子样+前一周期的补偿算法见《捷联惯导算法与组合导航原理》-P30)
- \(C_{n(m-1)}^{n(m)}=(C_{n(m)}^{n(m-1)})^T=[\exp(\phi_{in(m)}^n)]^T=[\exp(T_{[m-1,m]}\omega_{in(m)}^n)]^T\) 通常在导航更新周期\([t_{m-1},t_m]\)内,可以认为速度和位置引起的\(w_{in}^n\)变化很小,可作为常数,直接乘以周期即可。

误差分析
基本方法——误差分析的思路

误差方程的形式:
假设给定微分方程:
\[ \begin{aligned} \dot{z}=x+y \end{aligned} \tag{1} \]
且:
\[ \begin{aligned} \tilde{z}&=z+\delta z \\ \tilde{x}&=x+\delta x \\ \tilde{y}&=y+\delta y \end{aligned} \tag{2} \]
则误差方程的形式为:
\[ \begin{aligned} \delta \dot{z}= ??? \end{aligned} \]
写出考虑误差时的微分方程
即把\(\dot{z}=x+y\)使用带有误差的变量代替,得到:
\[ \begin{aligned} \tilde{\dot{z}}=\tilde{x}+\tilde{y} \end{aligned} \tag{3} \]
- 把(2)的代入到等式(3)
\[ \begin{aligned} \dot{z}+\delta{\dot{z}}=x+\delta x+ y+ \delta y \end{aligned} \tag{4} \]
- 取原微分方程(1),代入(4)
\[ \begin{aligned} \because \dot{z}&=x+y \\ \therefore x+y + \delta \dot{z}&=x + y+ \delta x+\delta y \\ \therefore \delta \dot{z}&=\delta x+ \delta y \end{aligned} \tag{5} \]
姿态误差分析





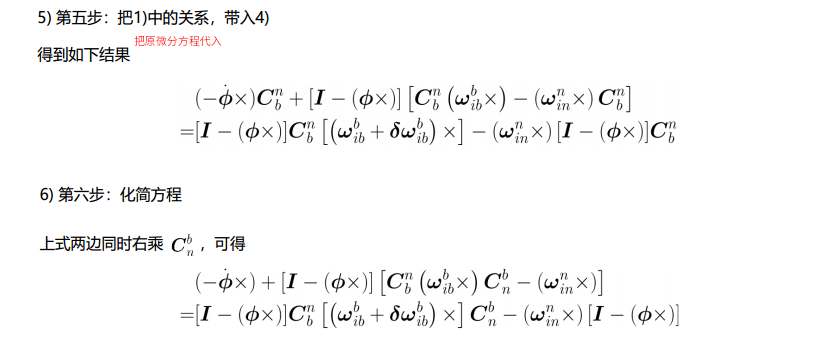

速度误差分析

位置误差分析

总结