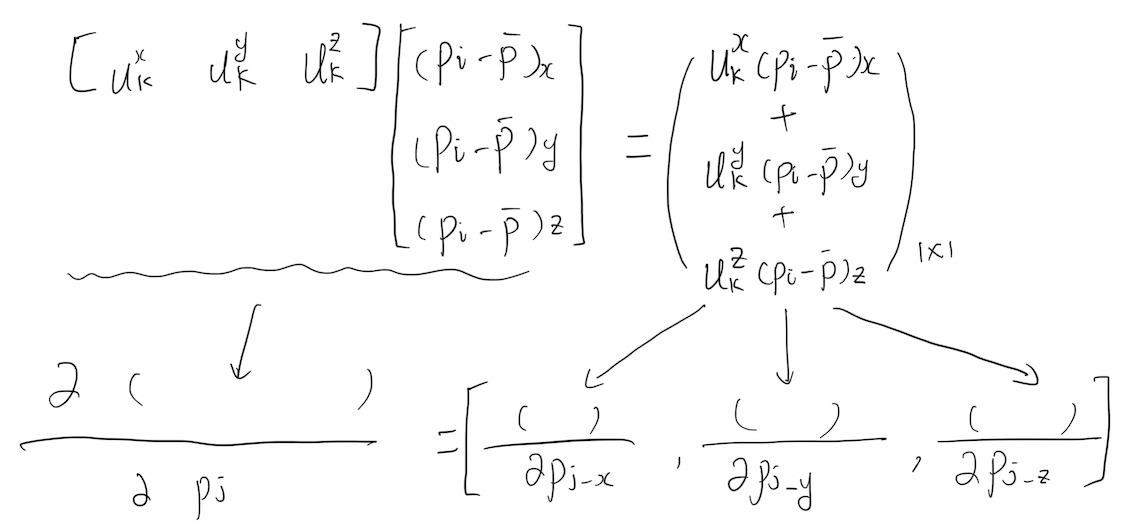BALM: Bundle Adjustment for Lidar Mapping

摘要
提出的方法通过最小化协方差矩阵的特征值来使得特征点分布在同一个边缘线或者平面上。为了加速求解,推到了微分,二阶闭式解。此外,还提出了自适应的体素滤波方法用来快速搜索特征关联。
介绍
增量式构建地图会由于环境退化或者较小视场角雷达而导致累计误差快速增大。降低这种漂移的其中一种方法是在激光雷达扫描的滑动窗口上执行局部BA,这使我们能够基于后续扫描中的新信息来重新评估过去的扫描,该方法已广泛用于视觉导航,并被证明是非常有效的。
由于直接进行深度测量,虽然激光雷达BA看起来比视觉BA更简单,但其公式实际上更复杂。因为在视觉BA,观测是高分辨率的图像,即每一个像素都可关联一个空间特征,如下图1,因此目标很明确,即最小化重投影误差。
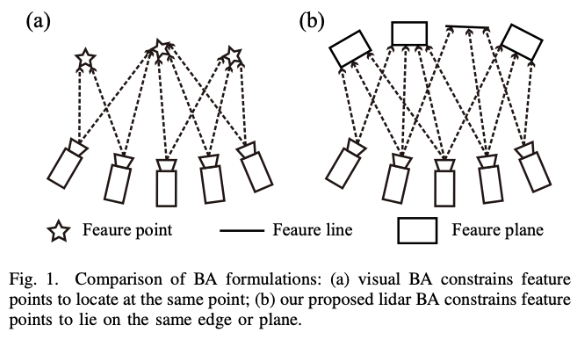
然而,这个并不适用于激光雷达,因为激光雷达点云非常稀疏,甚至是非重复的,因此无法进行精确的点对点匹配。
文章贡献:
- 提出了激光雷达BA框架,不像视觉ba那样,而是通过最小化协方差矩阵来约束特征点到边缘线或者平面的距离,还推到了cost func(如特征值)对激光雷达位姿的梯度和Hessian矩阵
- 提出了自适应体素化方法来快速搜索特征关联
效果:
BA推导
问题描述
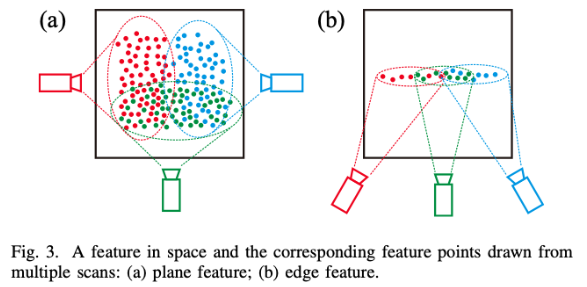
给定一组稀疏特征点\(p_{fi}(i=1,\cdots,N)\) ——从M帧扫描中提取的,并且都关联到同一个特征上(平面或者边缘线),如图3
假设第i个特征点从第\(s_i\)帧提取,其中
- \(i\in \{1,\cdots,N\}\)
- \(s_i \in \{1,\cdots,M\}\)
- M帧的位姿记为\(T=(T_1,\cdots,T_M)\)
那么,在全局地图上的特征点可以这样表示:
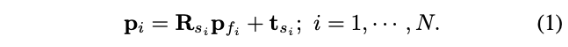
如先前所定义,激光雷达BA的问题是共同确定M扫描的姿势和全局3D点,现在3D地图是一个单一特征(边缘或平面),然后BA问题是联合确定姿态T和该特征的位置位置,这由特征上的点q和单位矢量n表示(n是平面的法线向量或边缘的方向)
对于平面特征
直接BA公式是最小化每个平面特征点到平面的距离,即:
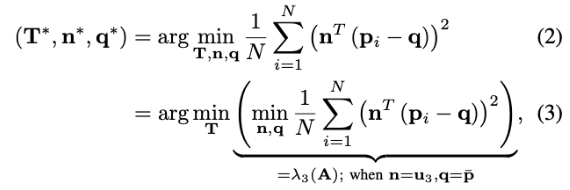
- \(p_i\):根据待估计位姿投影到全局地图上的特征点
- \(q\):某个特征上的点(边缘线内、平面内)
- \(\vec{n}\): 边缘线的方向向量或者是平面法向量
- 因此,上式即为最小化投影点到特征的距离
问:为啥当平面法向量取最小特征向量以及q取质心时,式(3)达到最小值,同时最小值即为最小特征值\(\lambda_3(\mathbf{A})\) ?
答:公式(3)中的问题等价于:
\[ \arg \min _{\mathbf{T}, \mathbf{n}, \mathbf{q}} \mathbf{n}^T\left(\min _{\mathbf{q}} \frac{1}{N} \sum_{i=1}^N\left(\mathbf{p}_i-\mathbf{q}\right)\left(\mathbf{p}_i-\mathbf{q}\right)^T\right) \mathbf{n} \]
通过对上式括号部分进行求导:
不难得到:
\[ \mathbf{q}^*=\frac{1}{N} \sum_{i=1}^N \mathbf{p}_i \]
(实际上,\(\mathbf{q}^*\)是平面上的点都能满足)
接下来,令:
\[ \mathbf{A} = \frac{1}{N} \sum_{i=1}^N\left(\mathbf{p}_i-\mathbf{q}^*\right)\left(\mathbf{p}_i-\mathbf{q}^*\right)^T \]
那么,原优化问题转化为:
\[ \arg \min _{\mathbf{T}, \mathbf{n}} \mathbf{n}^T \mathbf{A n} \]
此时,根据瑞利商定理,对称矩阵\(\mathbf{M}\)满足如下性质:
\[ \lambda_{\min }(\mathbf{M}) \leq \frac{\mathbf{x}^T \mathbf{M x}}{\mathbf{x}^T \mathbf{x}} \leq \lambda_{\max }(\mathbf{M}), \forall \mathbf{x} \neq \mathbf{0} \]
最终,原BA问题得到了与特征(\(\mathbf{n}, \mathbf{q}\))无关的闭式解,从而简化了BA问题为如下:
\[ \mathbf{T}^*=\arg \min _{\mathbf{T}} \lambda_{\min }(\mathbf{A}) \]
质心\(\bar{p}\)和A如下:
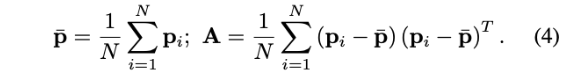
式(3)表明,优化特征点位置以及特征法向量(方向向量)可以写成关于位姿T的函数,因此只需要对位姿T进行优化。
同时,BA问题简化为通过调整激光雷达位姿\(\mathbf{T}\)来最小化(4)中定义的点协方差矩阵\(\mathbf{A}\)的最小特征值\(\lambda_3\)
对于边缘线特征
与平面特征类似,边缘特征的直接BA公式是将每条边特征点\(p_i\)到边的总平方距离最小化:
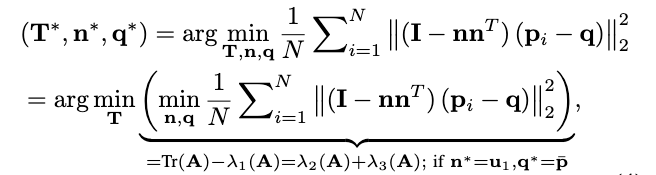
其中,\(\operatorname{Tr}(\mathbf{A})=\frac{1}{N} \sum_{i=1}^N\left\|\mathbf{p}_i-\overline{\mathbf{p}}\right\|_2^2\)表示矩阵\(\mathbf{A}\)的秩
请注意,在平面特征和边缘特征成本函数中,最佳点\(\mathbf{q}^*\)并非唯一的,因为点可以自由在平面内移动(或沿边缘移动),然而,这对要优化的最终成本函数没有影响
总而言之,激光雷达BA的目标是最小化每个项之和,其中每个项的形式如下:

为了快速优化求解,下面推导对于位姿T的微分的闭式解,最高2阶。
根据链式法则,首先对点\(p\)求导
微分
定理一
对于一组\(p_i(i=1,\cdots,N)\)以及式(4)定义的协方差矩阵\(A\)。假设矩阵\(A\)有特征值\(\lambda_k\)及其对应的特征向量\(u_k(k=1,2,3)\),则有\(\lambda_k\)对点\(p_i\)的偏导:
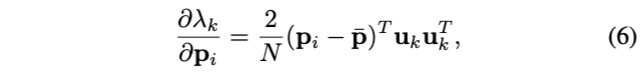
其中,\(\bar{p}\)是N个点的均值。
定理二
对于一组投影到世界坐标系的点\(p_i(i=1,\cdots,N)\)以及式(4)定义的协方差矩阵\(A\)。假设矩阵\(A\)有特征值\(\lambda_k\)及其对应的特征向量\(u_k(k=1,2,3)\),则有\(\lambda_k\)对点\(p_j\)的偏导*\(\lambda_k\)对点\(p_i\)的偏导:
- 当\(i \neq k\)时, \(\lambda_i \neq \lambda_k\)
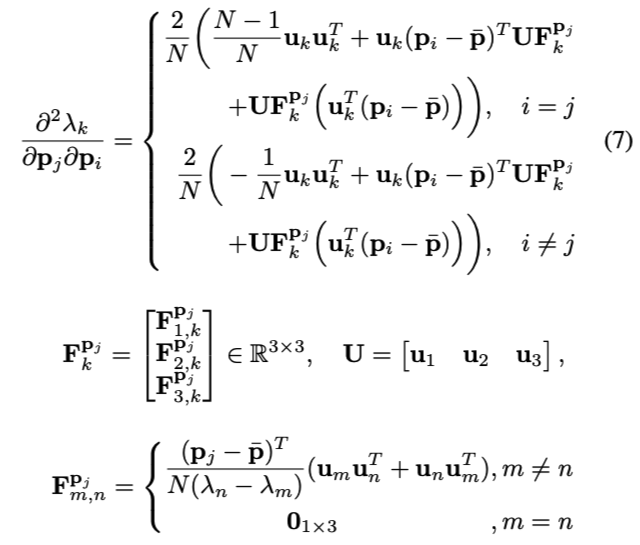
二阶微分
利用上述的一阶导和二阶导,可以使用如下二阶近似来近似式(5)的cost function
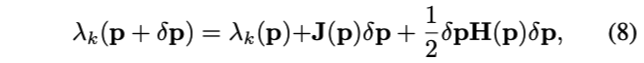
其中,
- \(J(p)\) 是雅可比矩阵,第i个元素按式(6)计算
- \(H(p)\) 是Hessian矩阵,其中第i行第j列元素按式(7)计算
回想一下,点向量p进一步依赖于式(1)中的扫描位姿\(T\)
因此,按照链式求导法则,还需要求出 点对位姿的导数,这个可以参考 《14讲》
如果对位姿\(T_j\)在其切平面进行扰动\(\delta T_j[\phi_j^T , \delta t_j^T]^T\),使用\(\boxplus\)表示,则有:
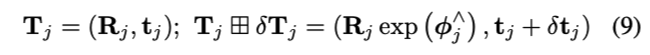
和
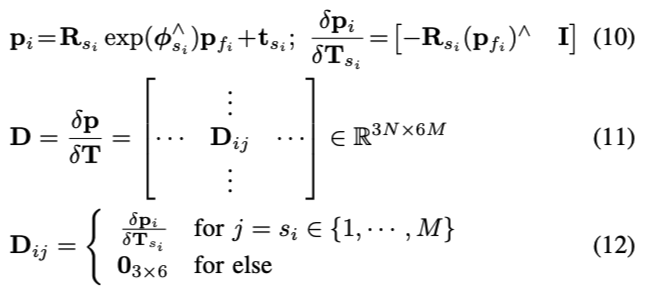
将式(12)带入式(8),可得:
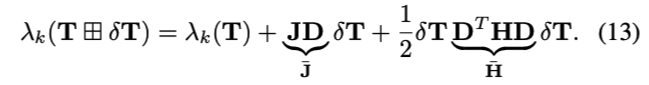
也就是说,特征值\(\lambda_k\)对位姿的求导实际上是: \(JD\)
最后,就可以使用LM迭代求解增量了
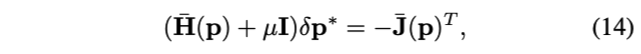
附录A
证明:定理一
记点\(\mathbf{p}_i=\left[\begin{array}{lll}x_i & y_i & z_i\end{array}\right]^T\)以及特征向量矩阵\(\mathbf{U}=\left[\begin{array}{lll}\mathbf{u}_1 & \mathbf{u}_2 & \mathbf{u}_3\end{array}\right]^T\)。进一步定义p是\(\mathbf{p}_i\)的一个元素,p是\(x_i, y_i,z_i\)中的其中一个(标量)。根据定义,我们有
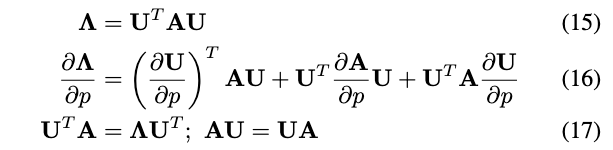
- \(\boldsymbol{\Lambda}\)是对角化后的矩阵
将式(17)代入到式(16),可得:
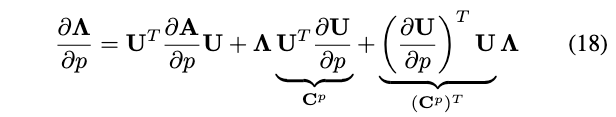
因为是特征值分解,所以有\(\mathbf{U}^T \mathbf{U}=\mathbf{I}\),进一步的,在\(\mathbf{U}^T \mathbf{U}=\mathbf{I}\)两边对p求偏微分得到如下:
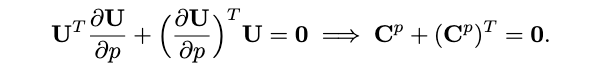
可以看出\(\mathbf{C}^p\)是一个反对称矩阵,其对角线元素为零。此外,由于\(\boldsymbol{\Lambda}\)是对角阵,也就是说式(18)右侧的最后两项\(\boldsymbol{\Lambda} \underbrace{\mathbf{U}^T \frac{\partial \mathbf{U}}{\partial p}}_{\mathbf{C}^p}+\underbrace{\left(\frac{\partial \mathbf{U}}{\partial p}\right)^T \mathbf{U} \boldsymbol{\Lambda}}_{\left(\mathbf{C}^p\right)^T}\)在对角线位置上的和为零。因此,仅考虑式(18)中的对角线元素可得(因为我们的目标是求特征值对位姿T的偏导,矩阵\(\boldsymbol{\Lambda}\)的对角线即为特征值):
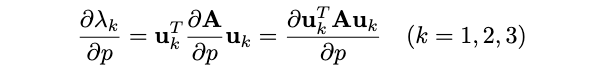
在第二个方程中,向量\(\mathbf{u}_k\)被视为常数。现在,将标量p换回点向量\(p_i\),即对上式进行堆叠,可得:
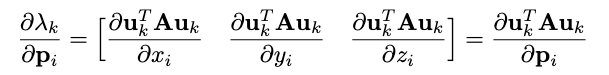
回想一下(3)中矩阵A的定义,以及下面的约束:
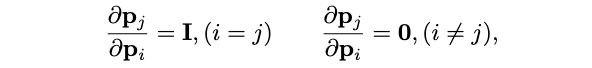
最终,我们得到如下偏导:
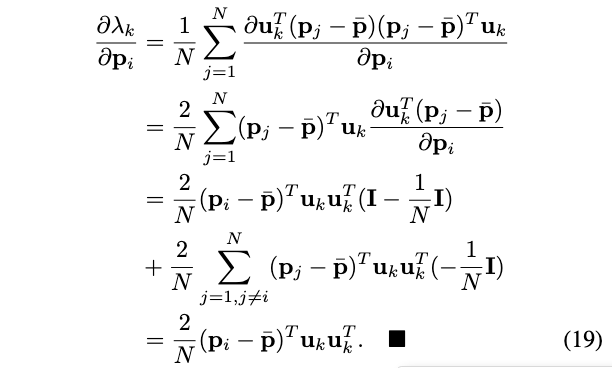
其中,
- \(\mathbf{u}_k^T\left(\mathbf{p}_j-\overline{\mathbf{p}}\right)\left(\mathbf{p}_j-\overline{\mathbf{p}}\right)^T \mathbf{u}_k\) = \(\left(\mathbf{p}_j-\overline{\mathbf{p}}\right)^T \mathbf{u}_k \mathbf{u}_k^T\left(\mathbf{p}_j-\overline{\mathbf{p}}\right)\)
- 可以看做是关于点\(p_i\)的函数\(\mathbf{B}(p_i) = \mathbf{P}^{T}(p_i) \mathbf{P}(p_i)\),其中\(\mathbf{P}(p_i) = \mathbf{u}_k^T\left(\mathbf{p}_j-\overline{\mathbf{p}}\right)\)
- 那么,可以将上面的求导看作是链式求导:
\[ \begin{aligned} \frac{\partial \lambda_k}{\partial \mathbf{p}_i} &=\frac{1}{N} \sum_{j=1}^N \frac{\partial \mathbf{B}(p_i)}{\partial p_i} \\ &=\frac{1}{N} \sum_{j=1}^N \frac{\partial \mathbf{P}^{T}(p_i) \mathbf{P}(p_i)}{\partial p_i} \\ &=\frac{1}{N} \sum_{j=1}^N 2 (\mathbf{P}^{T}(p_i))_{const} \frac{\partial \mathbf{P}(p_i)}{\partial p_i} \\ \end{aligned} \]
- \(\overline{\mathbf{p}} = \frac{1}{N} \mathbf{p}_i\)
补充材料:
证明:定理二
考虑两个点\(\mathbf{p}_i=\left[\begin{array}{lll}x_i & y_i & z_i\end{array}\right]^T\)、\(\mathbf{p}_j= \left[\begin{array}{lll}x_j & y_j & z_j\end{array}\right]^T\),记\(q\)是点\(\mathbf{p}_j\)的一个元素(\(x_j\),\(y_j\)或\(z_j\)),因为特征向量矩阵\(\mathbf{U}\)是正交的(\(\mathbf{U}^T \mathbf{U}=\mathbf{I}\)),因此,两边同时求导后,有:
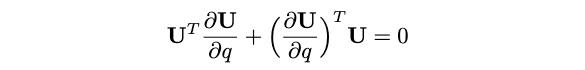
定义\(\mathbf{C}^q=\mathbf{U}^T \frac{\partial \mathbf{U}}{\partial q}\),则有:
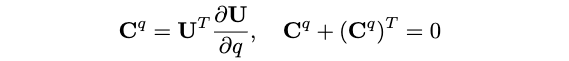
\(\mathbf{C}^q\)的对角线元素是零,与式(18)相似,使用q来替换p,有:
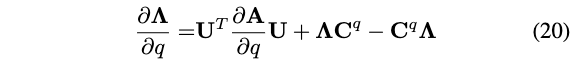
因为\(\boldsymbol{\Lambda}\)是对角线的,因此对于式(20)中\(\frac{\partial \boldsymbol{\Lambda}}{\partial q}\)的非对角线元素,我们有:
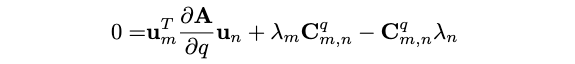
通过对上式进行反求,有\(\mathbf{C}_{m, n}^q\)是矩阵\(\mathbf{C}^q=\mathbf{U}^T \frac{\partial \mathbf{U}}{\partial q}\)的第m行,第n列的元素,如果\(\lambda_m \neq \lambda_n\),有:
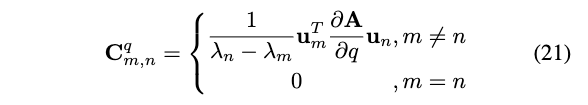
根据\(\mathbf{C}^q\)的定义:\(\mathbf{C}^q=\mathbf{U}^T \frac{\partial \mathbf{U}}{\partial q}\),有:
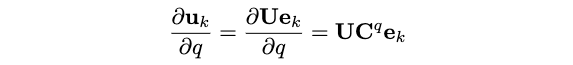
其中,
- \(\mathbf{e}_k\)是3x1的向量,并且第k个元素是1,其他是0
- 特征向量\(\mathbf{u}_m\) and \(\mathbf{u}_n\)被视为恒定向量
堆叠\(\mathbf{u}_k\)对\(\mathbf{p}_j\)的xyz三个分量的偏微分,有:
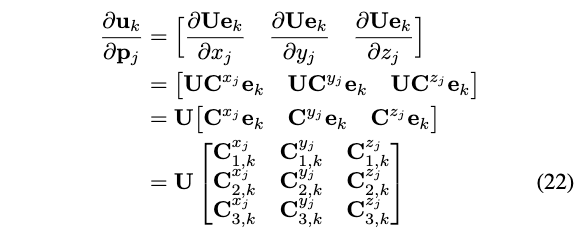
接下来,定义:

那么,式(22)可以表示为:
\[ \begin{aligned} \frac{\partial \mathbf{u}_k}{\partial \mathbf{p}_j}&=\left[\begin{array}{lll} \frac{\partial \mathbf{U} \mathbf{e}_k}{\partial x_j} & \frac{\partial \mathbf{U} \mathbf{e}_k}{\partial y_j} & \frac{\partial \mathbf{U} \mathbf{e}_k}{\partial z_j} \end{array}\right] \\ &= \mathbf{U}\left[\begin{array}{lll} \mathbf{C}_{1, k}^{x_j} & \mathbf{C}_{1, k}^{y_j} & \mathbf{C}_{1, k}^{z_j} \\ \mathbf{C}_{2, k}^{x_j} & \mathbf{C}_{2, k}^{y_j} & \mathbf{C}_{2, k}^{z_j} \\ \mathbf{C}_{3, k}^{x_j} & \mathbf{C}_{3, k}^{y_j} & \mathbf{C}_{3, k}^{z_j} \end{array}\right]\\ &= \mathbf{U} \left[\begin{array}{l} \mathbf{F}_{1, k}^{\mathbf{p}_j} \\ \mathbf{F}_{2, k}^{\mathbf{p}_j} \\ \mathbf{F}_{3, k}^{\mathbf{P}_j} \end{array}\right] \end{aligned} \]
即有:
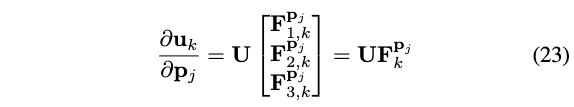
其中,根据定义,利用式(21)的xyz3个分量进行堆叠,可得:
\[ \begin{aligned} \mathbf{F}_{m, n}^{\mathbf{p}_j} &=\left[\begin{array}{lll} \mathbf{C}_{m, n}^{x_j} & \mathbf{C}_{m, n}^{y_j} & \mathbf{C}_{m, n}^{z_j} \end{array}\right] \in \mathbb{R}^{1 \times 3} \\ &=\left\{\begin{array}{cc} \frac{1}{\lambda_n-\lambda_m} \frac{\partial \mathbf{u}_m^T \mathbf{A} \mathbf{u}_n}{\partial \mathbf{p}_j}, & m \neq n \\ \mathbf{0} & , m=n \end{array}\right. \end{aligned} \]
进一步的,根据类似于式(19)的推导方法,可以进一步简化,得到:
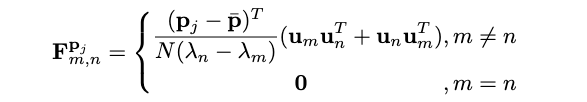
具体简化过程为:
根据性质:
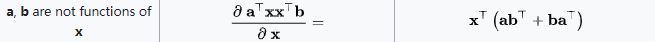
有:

现在,回过头来,我们需要求的是二阶导,有:
(因为\(\frac{\partial \lambda_k}{\partial \mathbf{p}_i}\)是 1x3 矩阵,但是Hessian是3x3矩阵,所以下面要对\(\frac{\partial \lambda_k}{\partial \mathbf{p}_i}\)的结果进行转秩,使得 3x1向量 对 1x3向量求导,才能得到3x3矩阵)
\[ \begin{aligned} \frac{\partial}{\partial \mathbf{p}_j}\left(\frac{\partial \lambda_k}{\partial \mathbf{p}_i}\right)&= \frac{2}{N} \frac{\partial \left ( \left(\mathbf{p}_i-\overline{\mathbf{p}}\right)^T \mathbf{u}_k \mathbf{u}_k^T \right)^{T}}{\partial \mathbf{p}_j} \\ &= \frac{2}{N} \frac{\partial \mathbf{u}_k \mathbf{u}_k^T \left(\mathbf{p}_i-\overline{\mathbf{p}}\right) }{\partial \mathbf{p}_j} \\ &= \frac{2}{N} \frac{\partial \mathbf{u}_k \left ( \mathbf{u}_k^T \left(\mathbf{p}_i-\overline{\mathbf{p}}\right) \right ) }{\partial \mathbf{p}_j} \\ &= \frac{2}{N} \left( \frac{\partial \mathbf{u}_k }{ \partial \mathbf{p}_j } \left ( \mathbf{u}_k^T\left(\mathbf{p}_i-\overline{\mathbf{p}}\right) \right ) + \mathbf{u}_k \frac{\partial \left ( \mathbf{u}_k^T\left(\mathbf{p}_i-\overline{\mathbf{p}}\right) \right )}{\partial \mathbf{p}_j} \right) \\ &= \frac{2}{N} \left( \frac{\partial \mathbf{u}_k }{ \partial \mathbf{p}_j } \left ( \mathbf{u}_k^T\left(\mathbf{p}_i-\overline{\mathbf{p}}\right) \right ) + \mathbf{u}_k \mathbf{u}_k^T \frac{\partial \left(\mathbf{p}_i-\overline{\mathbf{p}}\right)}{\partial \mathbf{p}_j} + \mathbf{u}_k \left(\mathbf{p}_i-\overline{\mathbf{p}}\right)^{T} \frac{\partial \mathbf{u}_k }{ \partial \mathbf{p}_j } \right) \end{aligned} \]
注意:\(\mathbf{u}_k^T\left(\mathbf{p}_i-\overline{\mathbf{p}}\right)\)是一个标量,所以\(\frac{\partial\left(\mathbf{u}_k^T\left(\mathbf{p}_i-\overline{\mathbf{p}}\right)\right)}{\partial \mathbf{p}_j}\)的结果应该是1x3的矩阵,在求导过程中,对他展开,就可以得到两项了,大概过程如下:
此时,将式(19)的\(\frac{\partial \lambda_k}{\partial \mathbf{p}_i}\)和式(23)的\(\frac{\partial \mathbf{u}_k}{\partial \mathbf{p}_j}\)代入上式,可得:
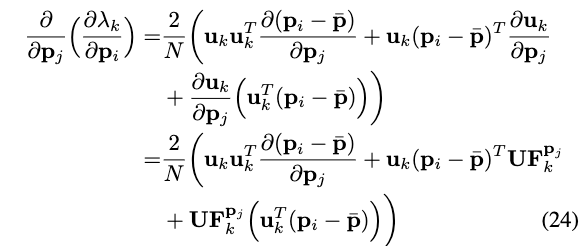
进一步的,又因为有:

代入式(24),可以得到最终结果: