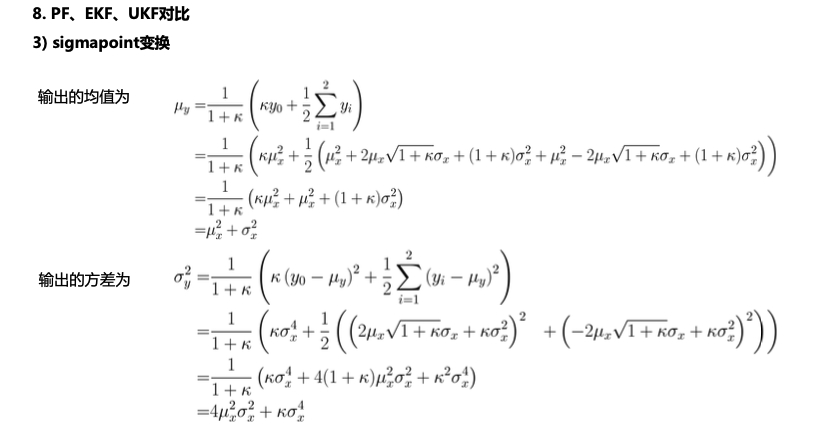基于滤波的融合方法


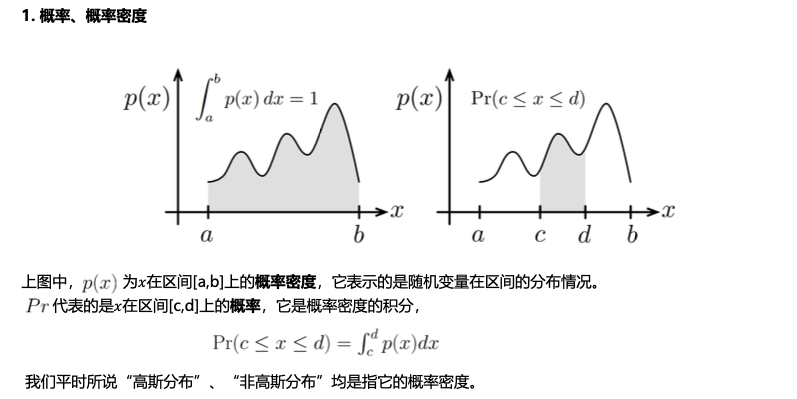
概率相关基础

贝叶斯公式和贝叶斯推断——核心

高斯概率密度函数——核心




上式说明,如果有(x,y)的联合概率密度函数,同时又有y的分布,那么就可以求出x关于y的条件概率密度,假设y是传感器观测的分布,而x是待求的状态量的话,那么相当于可以求出后验概率
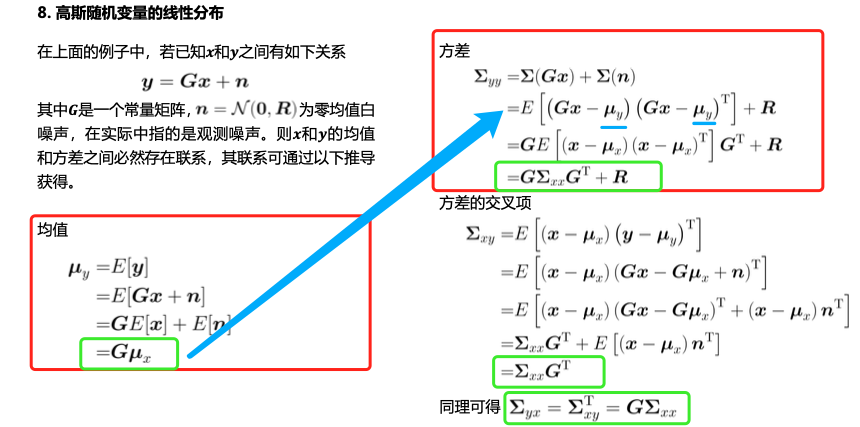
- 上图专门用来求后面观测量的均值和方差的
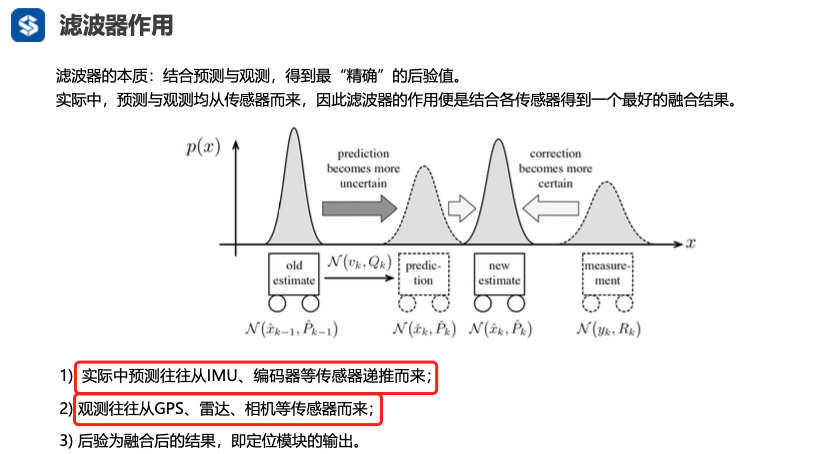
滤波器基本原理
滤波器的目的是求最大后验概率
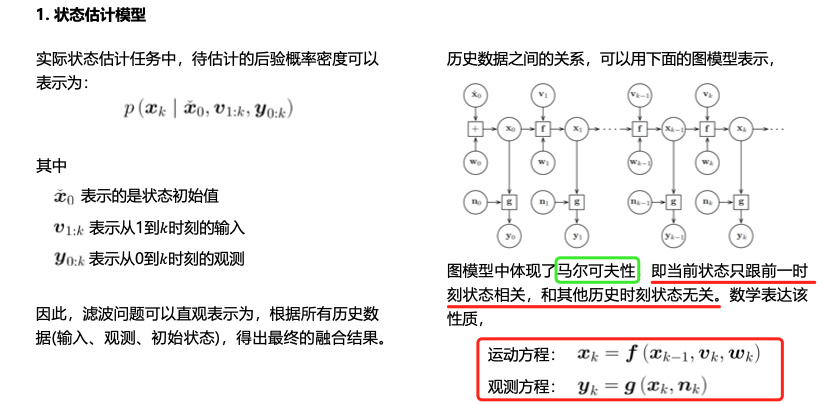

贝叶斯滤波器
详细推导
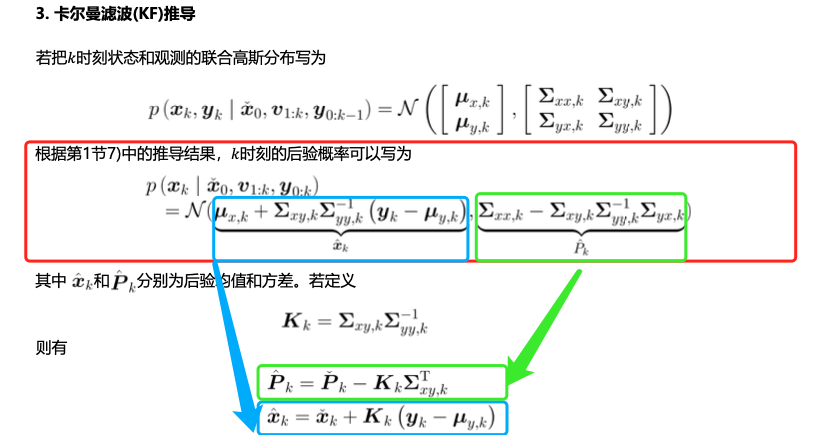
待估计的后验概率密度:
\[ \begin{aligned} p(x_k|x_0,v_{1:k},y_{0:k}) \end{aligned} \]
意思为,给定
- 初始状态\(x_0\)
- 1-k时刻的输入\(v_{1:k}\)
- 以及0-k时刻的观测\(y_{0:k}\)
发生状态为\(x_k\)的概率,我们后面的操作,就是为了求解\(x_k\),使得这个概率最大化
\[ \begin{aligned} p(x_k|x_0,v_{1:k},y_{0:k})&= p(x_k|x_0,v_{1:k},y_{0:k-1},y_k) \\ &= \frac{p(x_k,x_0,v_{1:k},y_{0:-1},y_k)}{p(x_0,v_{1:k},y_{0:k-1},y_k)} \\ &=\frac{p(y_k|x_k,x_0,v_{1:k},y_{0:k-1}) p(x_k|x_0,v_{1:k},y_{0:k-1}) p(x_0,v_{1:k},y_{0:k-1})}{p(y_k|x_0,v_{1:k},y_{0:k-1}) p(x_0,v_{1:k},y_{0:k-1})} \\ &= \frac{p(y_k|x_k,x_0,v_{1:k},y_{0:k-1}) p(x_k|x_0,v_{1:k},y_{0:k-1})}{p(y_k|x_0,v_{1:k},y_{0:k-1})} \\ &= \eta p(y_k|x_k,x_0,v_{1:k},y_{0:k-1}) p(x_k|x_0,v_{1:k},y_{0:k-1}) \end{aligned} \]
又因为观测方程中,\(y_k\)仅和\(x_k\)有关,所以进一步简化:
\[ p(x_k|x_0,v_{1:k},y_{0:k})=\eta p(y_k|x_k) p(x_k|x_0,v_{1:k},y_{0:k-1}) \]
接下来进一步化简上式右侧一项\(p(x_k|x_0,v_{1:k},y_{0:k-1})\)
根据\(p(x)=\int p(x|y) p(y) dy\)可得:
\[ \begin{aligned} p(x_k|x_0,v_{1:k},y_{0:k-1}) &= \frac{p(x_k,x_0,v_{1:k},y_{0:k-1})}{p(x_0,v_{1:k},y_{0:k-1})} \\ &= \int \frac{p(x_k,x_0,v_{1:k},y_{0:k-1}|x_{k-1}) p(x_{k-1})}{p(x_0,v_{1:k},y_{0:k-1})} d x_{k-1} \\ &= \int \frac{p(x_k,x_{k-1},x_0,v_{1:k},y_{0:k-1})}{p(x_{k-1},x_0,v_{1:k},y_{0:k-1})} \frac{p(x_{k-1},x_0,v_{1:k},y_{0:k-1})}{p(x_0,v_{1:k},y_{0:k-1})} d x_{k-1} \\ &= \int p(x_k|x_{k-1},x_0,v_{1:k},y_{0:k-1}) p(x_{k-1}|x_0,v_{1:k},y_{0:k-1}) d x_{k-1} \\ &= \int p(x_k| x_{k-1},v_k) p(x_{k-1}|x_0,v_{1:k},y_{0:k-1}) d x_{k-1} \end{aligned} \]
最后一步的化简是因为,k时刻的状态仅与k-1时刻的状态\(x_{k-1}\)和对应的输入有关
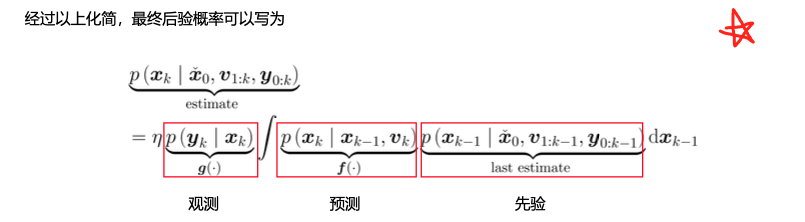
最终后验概率可以写成

其中,先验项就是k-1时刻下的后验概率。
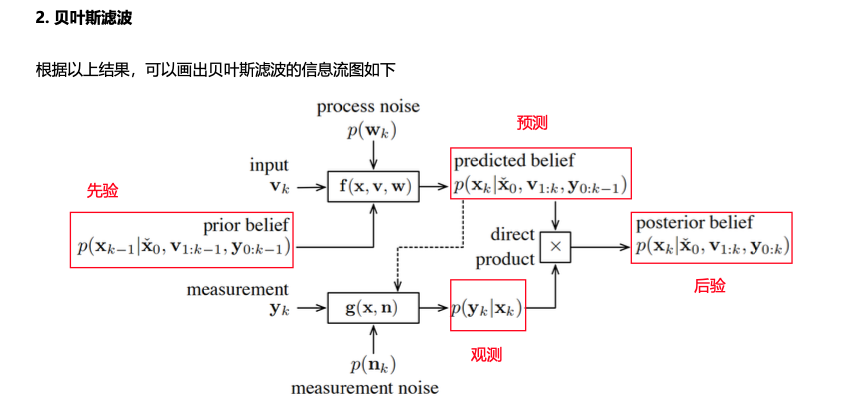
如何使用上面的推导? ————贝叶斯滤波器
卡尔曼滤波器

回顾: 多元联合高斯概率密度的分解

- 可参考:第四讲(拓展)_高斯过程(边缘化与条件作用)-联合高斯分布的分解 - 舒尔布顺序不一样,得到的结果不一样,但是实际上是等价的

回顾: 这里可用来求观测方程的均值和方差
因此,
- \(\Sigma_{xx}=\check{P_k}\)
- \(\Sigma_{xy}=\Sigma_{xx}G_k^T=\check{P}_k G_k^T\)
- \(\Sigma_{yx}=\Sigma_{xy}^T=G_k\check{P}_k^T=G_k\check{P}_k\)
- \(\Sigma_{yy}=G_k\check{P}_kG_k^T+C_k R_k C_k^T\)
所以,最终有:

- \(R\): 观测噪声
- \(Q\): 输入噪声,IMU噪声
扩展卡尔曼滤波器

- \(\hat{x}_{k-1}\) 预测方程线性化点,上一个时刻的更新值
- \(\check{x}_k\) 观测方程线性化点,是由预测方程得到的
对运动方程进行线性化之后,输入k-1时刻的更新后的状态\(\hat{x_{k-1}}\)以及控制输入\(w_k\),即可推导出预测值的均值和方差:

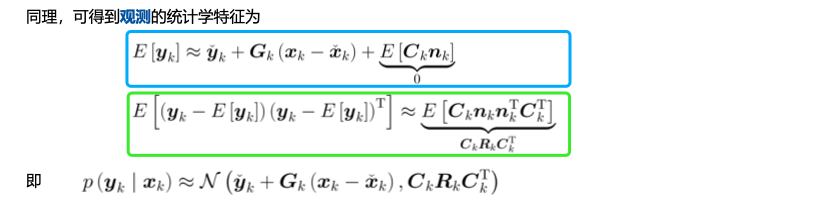
对观测方程进行线性化之后,即可得到观测的均值和方差:

推导套路
卡尔曼滤波
- 写出运动(预测)方程
- 写出观测方程
- 写出上一时刻(k-1)的后验分布,即更新后的状态值和方差
- 求预测值\(x_k\)的均值和方差 (利用线性高斯的性质)
- 求观测值\(y_k\)的均值和方差 (利用线性高斯的性质)
- 联合概率密度函数\(p(x_k,y_k)\)分解,得到后验概率\(p(x_k|y_k)\)的表示形式
- 将(4)(5)步求出来的均值和方差,带入(6)
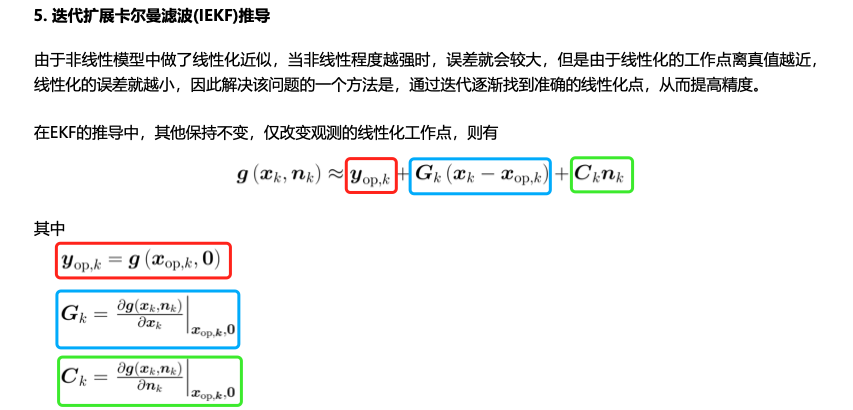
迭代扩展卡尔曼滤波(IEKF)

sigmapoint卡尔曼滤波(UKF/SPKF)
基本原理
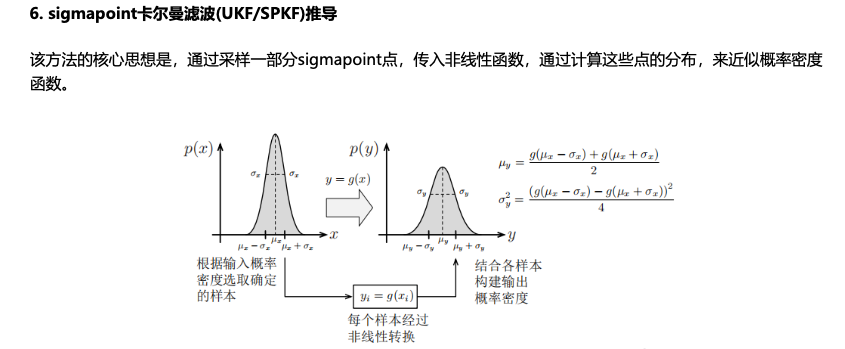
使用sigmapoint点进行采样,得到一个新的分布,并且计算均值和方差

预测步骤

更新步骤

粒子滤波器(PF)
UKF还是依赖高斯分布假设,而蒙特卡洛方法则基于大数定律
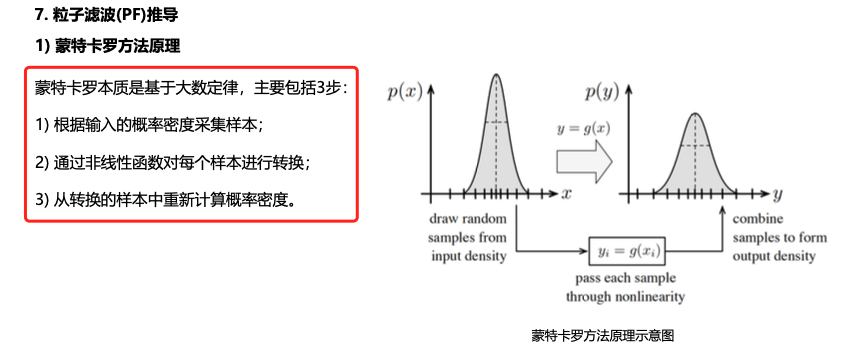
预测步骤

更新步骤

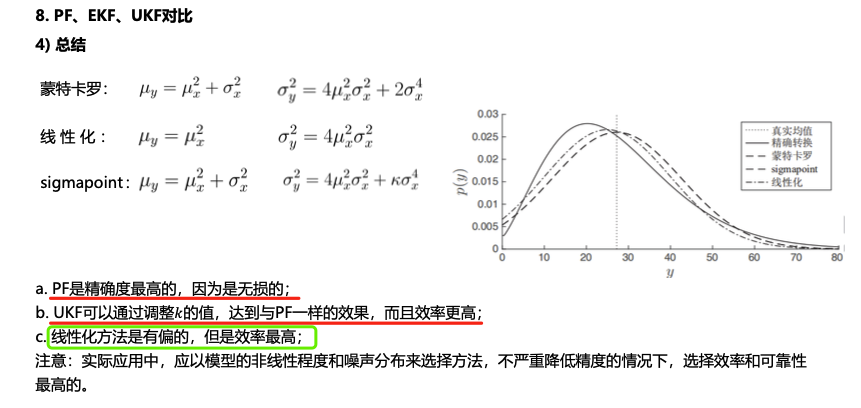
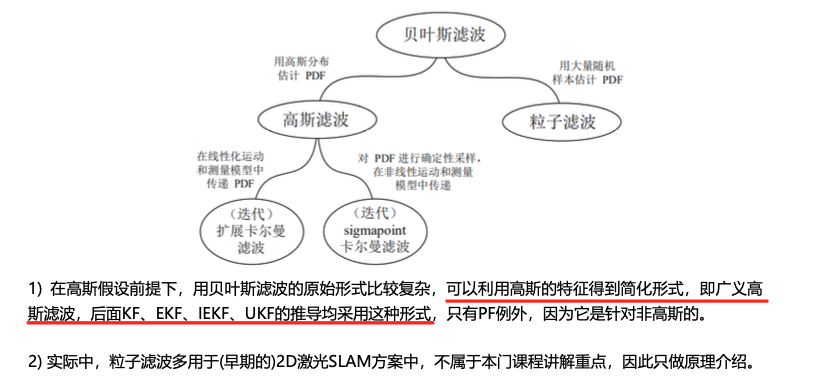
几种滤波方法对比