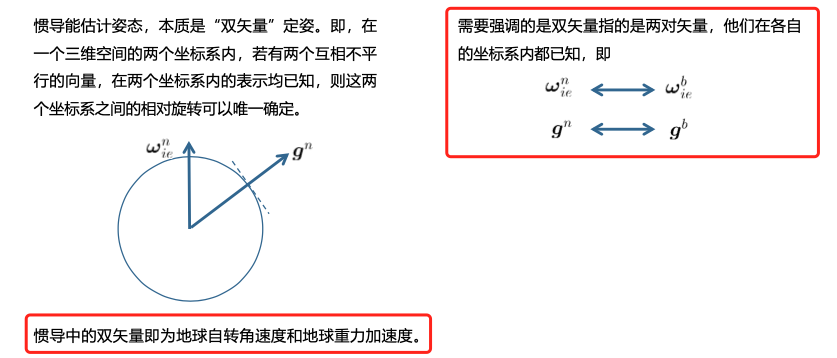
组合导航工程经验(重要)


初始对准:航向收敛
公式上理解现象
mems为什么不能做静态初始对准

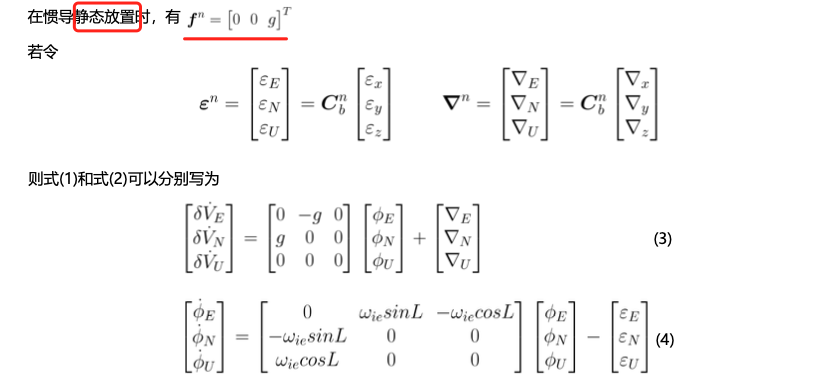
如果要解方程(3)
待求变量为:
- \(\phi_E\)
- \(\phi_N\)
- \(\phi_U\)
前两个比较好解,解\(\phi_U\)还需要用到方程组(4)
对方程组(3)展开,有:
\[ \begin{aligned} & \delta \dot{V}_E = -g \phi_N +\triangledown_E \\ & \delta \dot{V}_N = g \phi_E + \triangledown_N \\ & \delta \dot{V}_U = \triangledown_U \end{aligned} \]
如果对于高精度惯导,那么\(\triangledown_E , \triangledown_N \approx (1e-5g_0)\)可以忽略,所以,可以求得:
\[ \begin{aligned} & \phi_E = \frac{\delta \dot{V}_N}{-g} \\ & \phi_N = \frac{\delta \dot{V}_E}{g} \end{aligned} \]
对方程组(4)展开,有:
\[ \begin{aligned} \dot{\phi}_E = \phi_N (\omega_{ie}\sin L) - \phi_U (\omega_{ie}\cos L) + \epsilon_E \end{aligned} \]
由于\(\phi_E,\phi_N\)在前面已经求出来了,并且高精度惯导的\(\epsilon_E \approx 0.01\deg/h\)可以忽略
\[ \begin{aligned} \phi_U = \frac{C-\epsilon_E}{\omega_{ie} \cos L} \end{aligned} \]
其中,\(C\)是\(\phi_E,\phi_N\)组成的量

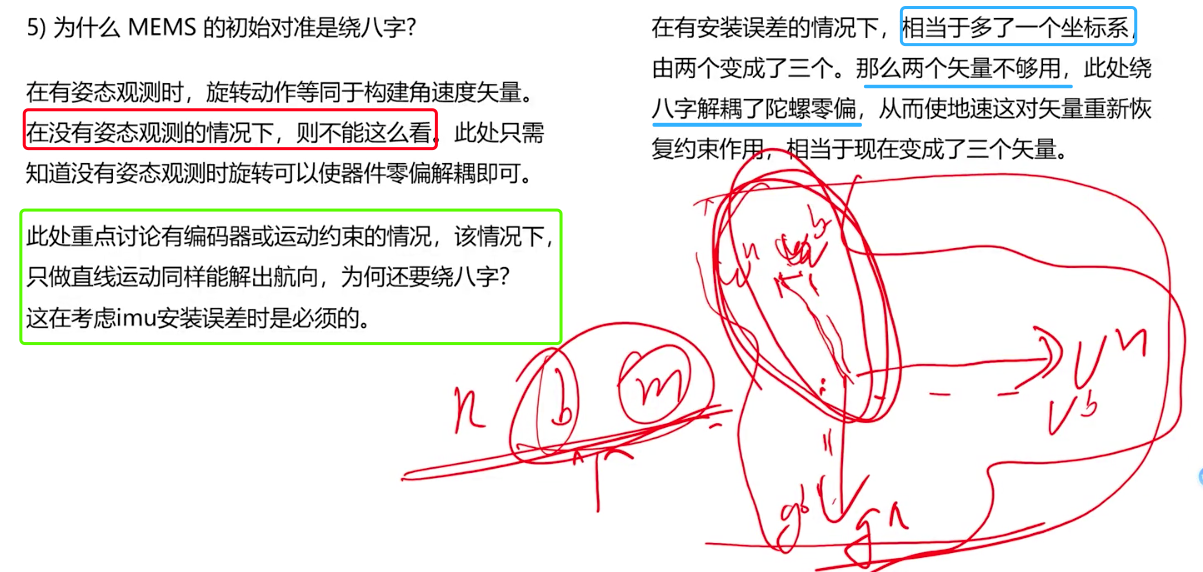
mems初始对准为什么需要绕8字
增加观测,增加矩阵的秩

加减速的收敛速度

mems直线行驶相关现象

从物理意义上理解