LINS: A Lidar-Inertial State Estimator for Robust and Efficient Navigation

ESKF模型
坐标系定义:
- \(\mathcal{F}_w\)表示固定的世界坐标系
- \(\mathcal{F}_{bk}\)表示第k个激光雷达时间步的imu坐标系
- \(\mathcal{F}_{lk}\)表示第k个激光雷达时间步的lidar坐标系
- local frame是指前一个激光雷达时间步的imu坐标系
状态定义
- \(x_w^{bk}\)表示\(\mathcal{F}_{bk}\)坐标系到\(\mathcal{F}_w\)世界坐标系的变换
- \(x_{bk+1}^{bk}\)表示从\(\mathcal{F}_{bk+1}\)坐标系到\(\mathcal{F}_{bk}\)坐标系的变换
\[ x_w^{bk} = [p_w^{bk},q_w^{bk}] \]
\[ x_{bk+1}^{bk} = [p_{bk+1}^{bk},v_{bk+1}^{bk},q_{bk+1}^{bk},b_a,b_g,g^{bk}] \]
误差状态定义
\[ \delta x=[\delta p, \delta v ,\delta \theta, \delta b_a , \delta b_g ,\delta g] \]
根据误差状态卡尔曼,一旦\(\delta x\)被估计出来,我们就可以获得最终的结果\(x_{bk+1}^{bk}\),通过向state nominal的\(^-x_{bk+1}^{bk}\)注入误差状态\(\delta\),即:
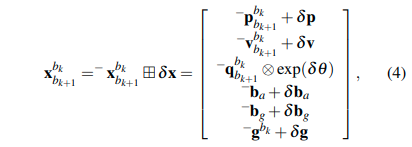
状态传播(预测)
这一步进行如下参数的传播
- 误差状态\(\delta x\)
- 误差状态协防差矩阵\(P_k\)
- state nominal的\(^-x_{bk+1}^{bk}\)
当新的imu测量到达,线性连续时间模型如下:
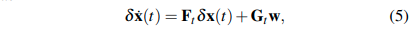
其中,
- \(w=[n_a^T,n_g^G,n_{ba}^T,n_{bg}^T]\),分别表示高斯噪声模型,与VINS-Mono一致
- \(F_t\)是误差状态转移矩阵
- \(G_t\)是噪声雅克比矩阵

论文公式有误,详细可参考 误差状态卡尔曼P69——The error state Jacobian and perturbation matrices 式(311)
其中,
- \([\cdot]_{\times} \in \R^{3\times 3}\)表示将3D向量转换成反对称矩阵
- \(R_t^{bk}\)表示将k时刻的imu坐标系转换到\(\mathcal{F}_{bk}\)坐标系的旋转
- \(\hat{a}^t,\hat{\omega}_t\)表示去除bias以及(重力影响?)的加速度计输出和陀螺仪输出
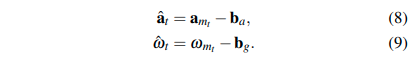
对式(5)进行离散化,得到离散时间的传播方程(预测)
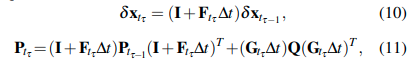
其中,
- \(\Delta_t=t_\tau-t_{\tau-1}\)
- \(t_\tau,t_{\tau-1}\)是imu数据时间戳
- Q表示噪声w的协方差矩阵,可以由离线的传感器参数标定获取
更新
文章的主要贡献在此
在iekf里面,更新步骤其实可以与优化问题建立关联:
参考文献:
- A review of point cloud registration algorithms for mobile robotics.
- Iterated extended kalman filter based visual-inertial odometry using direct photometric feedback.
即以误差状态作为待求解的变量\(\delta x\)
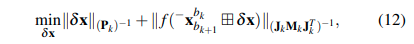
其中,
- \(f(\cdot)\)是残差函数,其输出是点——线、点——面距离的对叠向量
- \(||\cdot||\)是马氏距离
- \(J_k\)是残差函数\(f(\cdot)\)对观测噪声的雅克比
- \(M_k\)是观测噪声的协方差矩阵
当给定一个\(x_{bk+1}^{bk}\),\(f(\cdot)\)中关于点\(p_i^{lk+1}\)(\(\mathcal{F}_{lk+1}\)坐标系中的第i个点)的误差项可以描述如下:
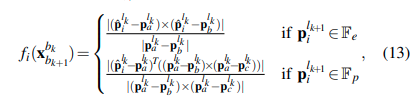
就是LOAM的距离计算公式
然后有:
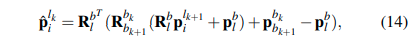
其中,
- \(\hat{p}_i^{lk}\)表示将点\(p_i^{lk+1}\)从\(\mathcal{F}_{lk+1}\)坐标系转换到\(\mathcal{F}_{lk}\)坐标系后的点
- \(R_l^b,p_l^b\)表示激光雷达到imu的外參(可离线标定获取)
关于式(13)的物理解释是:对于一个边缘线上的点,它描述了点\(\hat{p}_i^{lk}\)到与他相关联的边缘线\(p_a^{lk}p_b^{lk}\),对于平面点,同理 (就是LOAM嘛)
然后使用iekf来求解式(12)所描述的优化问题:
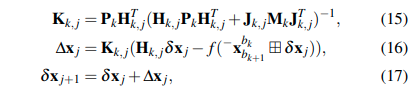
其中,
- \(\Delta x_j\)表示在第j次迭代的矫正,即求解出来的增量
- \(H_{k,j}\)表示\(f(^-x_{bk+1}^{bk}\boxplus\delta x_j)\)关于\(\delta x_j\)的雅克比
注意到,在每一次迭代中,将重新关联边缘线特征和平面特征,这样就可以重新计算\(H_{k,j},J_{k,j}和K_{k,j}\),相当于更新线性化点,重新关联特征
当\(f(x_{bk+1}^{bk})\)降低到一个特定的阈值,就对协方差\(P_k\)进行更新,结束迭代
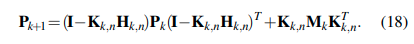
使用式(4),即可获取到最终的结果\(x_{bk+1}^{bk}\),然后还可以进行去畸变操作。
最后,可以对下一个状态\(x_{bk+2}^{bk+1}\)进行初始化:
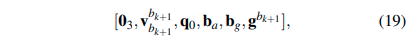
其中,
- \(q_0\)表示单位四元数
- \(v_{bk+1}^{bk+1}=R_{bk}^{bk+1}v_{bk+1}^{bk}\)
- \(g^{bk+1}=R_{bk}^{bk+1}g^{bk}\)
注意到,在协方差矩阵中,速度、bias、重力都保持,而其他关于相对位姿的项都被置零,因为相对于自身坐标系没有不确定性.
状态补偿
每一个更新步完成,需要对全局位姿\(x_w^{bk}\)进行更新,如下:
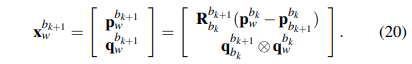
初始化
- 初始加速度bias,Lidar-imu外參都通过离线标定获取
- 初始的陀螺仪bias通过求均值获取
- 初始roll和pitch在运动之前可通过去除bias的加速度计算得到
- 初始的重力向量使用前面获取的roll和pitch将导航坐标系的重力向量转换到载体坐标系(imu系)获取