LiDAR Inertial Odometry Aided Robust LiDAR Localization System in Changing City Scenes

摘要
提出一种将激光惯性里程计(LIO)和激光扫描配定位模块进行整合,然后将两种观测融入到pose graph中进行联合优化的框架。基于激光扫描的global matching和 lio是互补的,这使的可以达到鲁棒的定位,以解决环境的短暂变化以及地图的误差问题,如图1所示。
本文贡献:
- 一种车辆定位的联合框架,可自适应融合激光扫描匹配和局部里程计,从而有效保护定位系统,使其免受城市场景变化的影响
- 一种LIO方法,并结合了占据栅格和激光强度
- 每天在拥挤繁忙的城市街道上经过严格测试的强大车辆定位系统,证明了其在充满挑战和动态变化的环境中的强大能力
相关工作
长期定位(Long-term Localization)
建立一个7天24小时的全天候定位系统是一项艰巨的任务,近年来受到了极大的关注。文献[6]表明,可以通过归一化每一帧的LiDAR扫描的亮度和标准偏差来调整由潮湿路面引起的较少反射率。文献[2][3]通过在地图中引入多分辨率高斯混合表示法,展示了一种强大的LiDAR定位系统,该系统可以通过道路翻修和降雪环境下运行。文献[5],LiDAR定位系统通过结合高度信息成功地通过了具有挑战性的路段,其中包括新建的墙壁和重新铺设的道路。文献[4]通过引入主成分分析(PCA)和边缘轮廓来增强其定位系统的鲁棒性,尤其是在下雨天或下雪天时。
这些工作着重于利用利基技术解决特定问题,但我们力图通过将里程表和全局匹配模块中的补充线索自适应地融合在一起,从而寻求更通用的解决方案。
其他工作如[7,8,9,10,11]解决了类似的长期定位问题,但使用的视觉传感器对时间,光线或天气导致的场景外观变化敏感。
激光惯性里程计(LiDAR Inertial Odometry)
目前有大量关于激光里程计的工作,如[12,13,14,15,16,17,18,19,20,21,22,23,24]。如[14],[18],[17],[17],惯性测量可通过提供先验估计并补偿运动失真来帮助解决问题。[18]构建更加紧密的局部运动约束,[23],[24]进一步建立紧密耦合的里程表。
在这项工作中,我们遵循Hess的工作[13],并将基于占用栅格的LiDAR惯性里程表集成到我们的定位框架中,因为它的地图表示与我们的全局匹配模块相似,并且与多个激光扫描仪兼容
融合定位方法
一类重要的是松耦合融合方法[25],[5],[26]利用误差状态卡尔曼滤波器并通过不同方法实现了松耦合的位姿估计。类似于[26],我们的方法不是使用卡尔曼滤波器,而是利用基于图的融合框架,该框架以每单位计算时间的精度更高的性能优于滤波方法[27],[28]。[29]展示了融合GNSS,LiDAR和惯性测量的紧密耦合导航系统。
系统框架
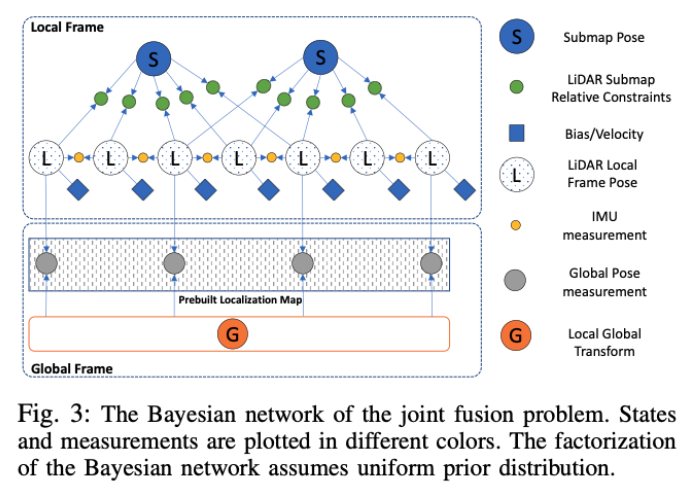
提出的系统包含四个模块:LiDAR惯性里程计(LIO),LiDAR全局匹配(LGM),基于姿态图的融合(PGF)和环境变化检测(ECD),如图2所示。
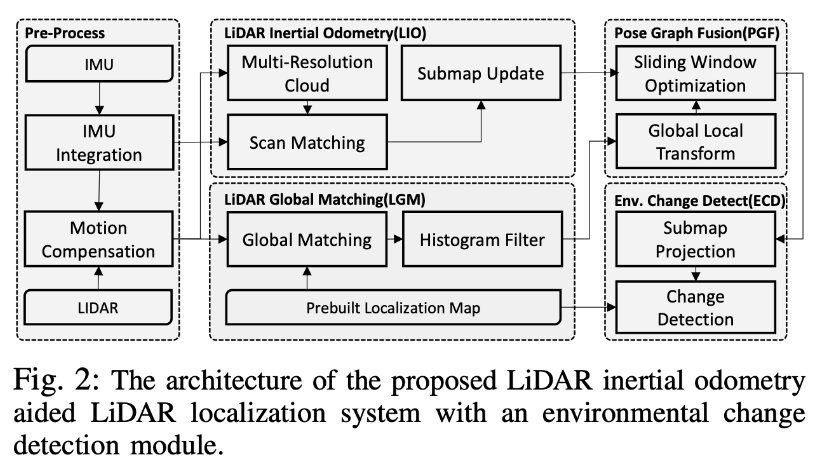
我们遵循G. Wan[5]等人的最新LiDAR定位工作来构建系统,并在我们的框架中将其作为子模块LGM。LGM模块是一种global定位方法,可将在线LiDAR扫描与预先构建的地图进行匹配,并进行3 DoF(x,y,yaw)估计,一旦我们成功地水平定位,就可以通过读取IMU重力测量值和数字高程模型(DEM)地图来估算其他3个自由度(侧倾,俯仰,高度)。
其他两个模块是,LIO和PGF,根据解决不同的最大后验概率(MAP)估计问题来实现。
最大后验概率(MAP)估计问题通常是在滑动窗口下定义的非线性优化问题,设\(\kappa\)记为窗口中的所有帧集合
- 滑动窗口中的状态\(\mathcal{X}=\left\{\mathbf{x}_{k}\right\}_{k \in \mathcal{K}}\)
- 观测集合分别记为\(\mathcal{Z}=\left\{\mathbf{z}_{k}\right\}_{k \in \mathcal{K}}\)
- 第k帧的状态\(\mathbf{x}_{k}=\left[\boldsymbol{\omega}_{k}, \mathbf{t}_{k}, \mathbf{v}_{k}, \mathbf{b}_{k}\right]\)分别表示旋转、位置、速度和bias,其中\(\omega_k\)是李代数中的\(so(3)\),即有\(R_k=\exp(\omega_k)\)。
提出的LIO框架
LiDAR惯性里程计在我们的系统中起着至关重要的作用,可在严峻的环境(例如,由于道路建设或恶劣天气导致的地图过期或环境变化)中提高定位性能。其中,激光里程计估计相邻帧的相对位姿变换,同时构建局部地图,称为子图,该子图始终是最新的,并且随着每个新的LiDAR SCAN不断更新。
我们的LiDAR惯性里程计的实现遵循W. Hess的工作[13] (注:cartographer),但有许多重要的扩展可提高其准确性。
- 使用了3d占据栅格来代替2d,来实现6自由度的里程计,这种扩展可将系统应用到3维环境中,如停车场结构或立交桥,同时简化了下面提到的imu预积分
- 重要的惯性测量数据被合并以提供运动预测和帧之间的相对约束,更重要的是,惯性测量的结合使我们能够对由载体运动引起的扭曲的LiDAR扫描进行运动补偿,为了控制计算时间,我们在实现中采用了[30]引入的惯性测量值的预积分
- 考虑到某些情况下来自车道或者路面标记的丰富信息,在占据栅格配准过程中整合了激光强度信息,用来补充每个网格单元的占用概率,它提供了有价值的环境纹理信息
- 最后,通过将多分辨率的占据栅格来实现求解非线性优化问题中的从粗到精细化的方法,它不仅有助于网格配准的收敛,而且可以避免计算需求
LIO问题描述:在给定先前的状态\(x_{k-1}^L\)、使用k-1帧更新后的子图\(\mathcal{S}_{k-1}\)以及观测\(z_k\),求状态\(x_{k}^L\)的最大后验概率。
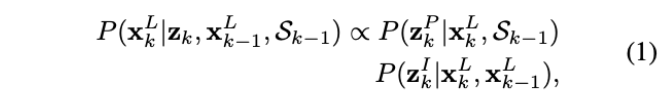
其中,\(\mathbf{z}_{k}=\left\{\mathbf{z}_{k}^{P}, \mathbf{z}_{k}^{I}\right\}\),\(\mathbf{z}_{k}\)和\(\mathbf{z}_{I}\)分别是点云和惯性测量的观测,上标\(L\)表示由子图和里程计表示的局部帧的状态\(\mathbf{x}_{k}^L\).
在零均值高斯似概率的假设下,观测的似然概率通过构建cost func来定义:
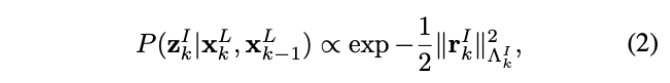
其中,\(\|\mathbf{r}\|_{\Lambda}^{2}=\mathbf{r}^{T} \Lambda^{-1} \mathbf{r}\),并且有:
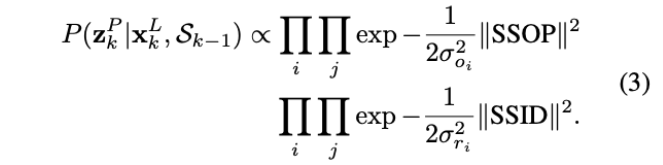
其中,
- 等式(2)根据imu预积分方法计算,可参考文献30
- 等式(3)中的
SSOP(Sum of Squared Occupancy Probability)和SSID(Sum of Squared Intensity Difference)分别代表占用栅格概率和LiDAR强度损失,其定义如下:
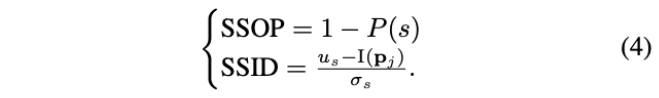
给定一个激光点\(\mathbf{p}_j \in \R^3\),一个分辨率为\(i\)的子图以及一个位姿状态\(\mathbf{x}_{k}^{L}=\left[\mathrm{R}_{k}, \mathbf{t}_{k}\right]\),子图中被击中的单元\(s\)可以被找到。\(P(s)\)是在分辨率i下击中子图的占用概率,这个占用概率的维持是通过以最大化后验概率\(P\left(\mathbf{x}_{k}^{L} \mid \mathbf{z}_{k}, \mathbf{x}_{k-1}^{L}, \mathcal{S}_{k-1}\right)\)的方法不断的将新的激光雷达扫描插入到子图中。
这个增量式升级问题可以通过使用inverse measurement模型以及[31]中引入的log adds ratio 的二进制贝叶斯滤波器来解决。
\(I(\mathbf{p}_j)\)是点\(\mathbf{p}_j\)的强度,\(u_s\)和\(\sigma_s\)是击中单元的激光强度均值和方差,(注:归一化到标准正态分布)。为了更好的确保配准性能,采用了三次插值从子图中获得概率和强度。方差\(\sigma_{Oi}\)和\(\sigma_{ri}\)用于在不同分辨率下对优化中的占据概率和强度项分别进行加权。
MAP估计值与负对数后验的最小值相对应,后者可以写为残差平方的总和,从而产生非线性最小二乘优化问题
位姿图融合
虽然LiDAR惯性里程计可以在局部坐标系中提供良好的相对约束,但我们仍然需要全局约束才能实现全局定位,baidu-LGM模块为我们的系统提供了全局定位信息,我们的LGM遵循[5].
将此融合问题公式化为MAP估计,并假设先验分布具有统一形式,将后验概率分解为:
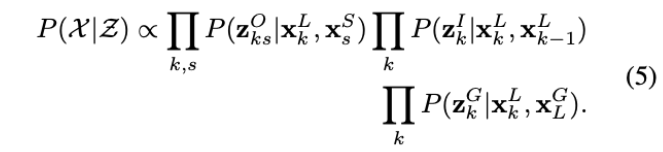
分解可以可视化为如图3所示的贝叶斯网络。在零均值高斯似概率的假设下,观测的似然概率如下:
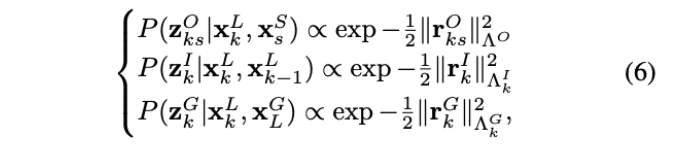
其中,\(\mathbf{r}_{k s}^{O}\)、\(\mathbf{r}_{k}^{I}\)、\(\mathbf{r}_{k}^{G}\)分别代表里程计、惯性测量、全局匹配的残差。
坐标系定义如下:
- Local Frame: 局部坐标系,如使用utm投影,再划分,以某个位置作为原点
- Global Frame: 全局坐标系,utm/wgs-84等
- Submap Pose: 子图相对于局部坐标系的位姿
- Lidar Local Frame: 激光雷达坐标系相对于局部坐标系的位姿
如果定义如下:
- 某帧相对于局部坐标系的位姿(待估计位姿):\(\mathbf{x}_{k}^{L}=\left[\mathrm{R}_{k}^{L},\mathbf{t}_{k}^{L}\right]\)
- 局部坐标系到全局坐标系的变换(应该是已知的):\(\mathbf{x}_{L}^{G}=\left[\mathrm{R}_{L}^{G}, \mathbf{t}_{L}^{G}\right]\)
- 由[5]中的LGM模块输出的全局位姿观测\(\mathbf{z}_{k}^{G}=\left[\mathrm{R}_{k}^{G}, \mathbf{t}_{k}^{G}\right]\)
- 全局残差可用如下表示: \(\left(\mathbf{r}_{k}^{G}\right)^{T}=\left[\log ^{T}\left(\mathrm{R}_{r G}\right), \mathbf{t}_{r G}^{T}\right]\),其中:
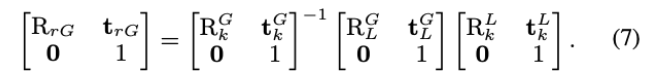
关于全局残差的协方差\(\Lambda_{k}^{G}\),我们将其写为:
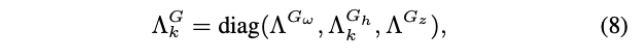
其中,
- \(\Lambda^{G_\omega} \in \R^{3\times3}\)是旋转协方差
- \(\Lambda^{G_{z}} \in \mathbb{R}^{1 \times 1}\)是高度方差
- 上述协方差矩阵是恒定的对角矩阵,因为我们的LGM模块仅使用[5]中讨论的2D直方图滤波器来估计水平定位的不确定性
- 如[5]中的等式12所示,相应地针对每个帧k计算水平匹配协方差矩阵\(\Lambda_{k}^{G_{h}} \in \mathbb{R}^{2 \times 2}\)
注意,此处介绍的不确定性估计对于定位系统的性能至关重要,从而产生自适应融合
关于里程计的残差问题,将会采用随着激光里程计的运行终结旧的子图更新并且创建新的子图。
由LIO模块输出的载体局部位姿与子图的之间的相对位姿关系约束\(\mathbf{z}_{ks}^O\)被构建并存在于滑动窗口的生命周期中。相似的,如果由如下定义:
- 某个子图的位姿:\(\mathbf{x}_{s}^{S}=\left[\mathrm{R}_{s}^{S}, \mathbf{t}_{s}^{S}\right]\)
- 某帧相对于子图的位姿观测: \(\mathbf{z}_{k s}^{O}=\left[\mathrm{R}_{k s}^{O}, \mathbf{t}_{k s}^{O}\right]\)
- 里程计残差可定义为: \(\left(\mathbf{r}_{k s}^{O}\right)^{T}=\left[\log ^{T}\left(R_{r O}\right), \mathbf{t}_{r O}^{T}\right]\)
其中,
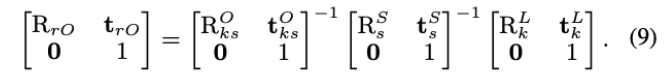
根据里程残差中的协方差\(\Lambda^O\),假设估计不确定性在所有帧之间均匀分布,我们在所有帧和子图上使用全局常数对角矩阵
惯性约束的预积分的处理方法与[30]中介绍的相同。 使用Ceres解算器[32]求解非线性最小二乘优化。
实验
传感配置:
- Velodyne HDL- 64E 360◦LiDAR
- NovAtel PwrPak7D-E1 GNSS RTK receiver integrated with dual antennas and an Epson EG320N IMU.
基准参考:
没有用rtk,用的啥离线slam方法?
The ground truth poses used in the evaluation are generated using offline LiDAR SLAM methods typically formulated as a large-scale global least-square optimization problem, which are beyond the scope of this work.
运行速度分析
- lio、pose graph fuse 运行在CPU上
- 全局激光匹配运行在FPGA上
