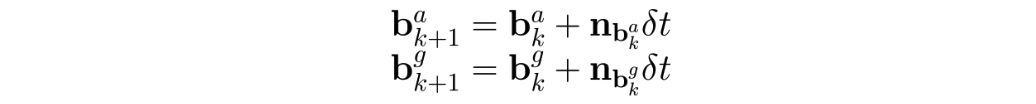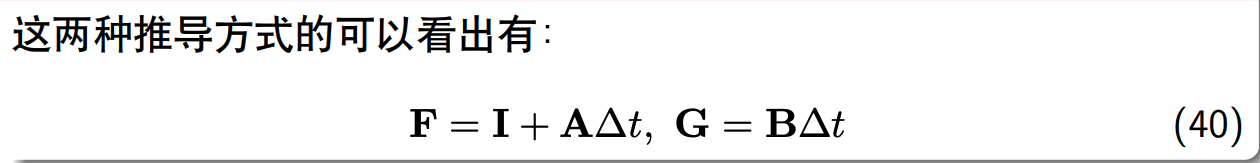- 1. 什么是预积分
- 2. 预积分计算
- 3. 预积分更新
- 4. 预积分(误差)协方差计算
什么是预积分
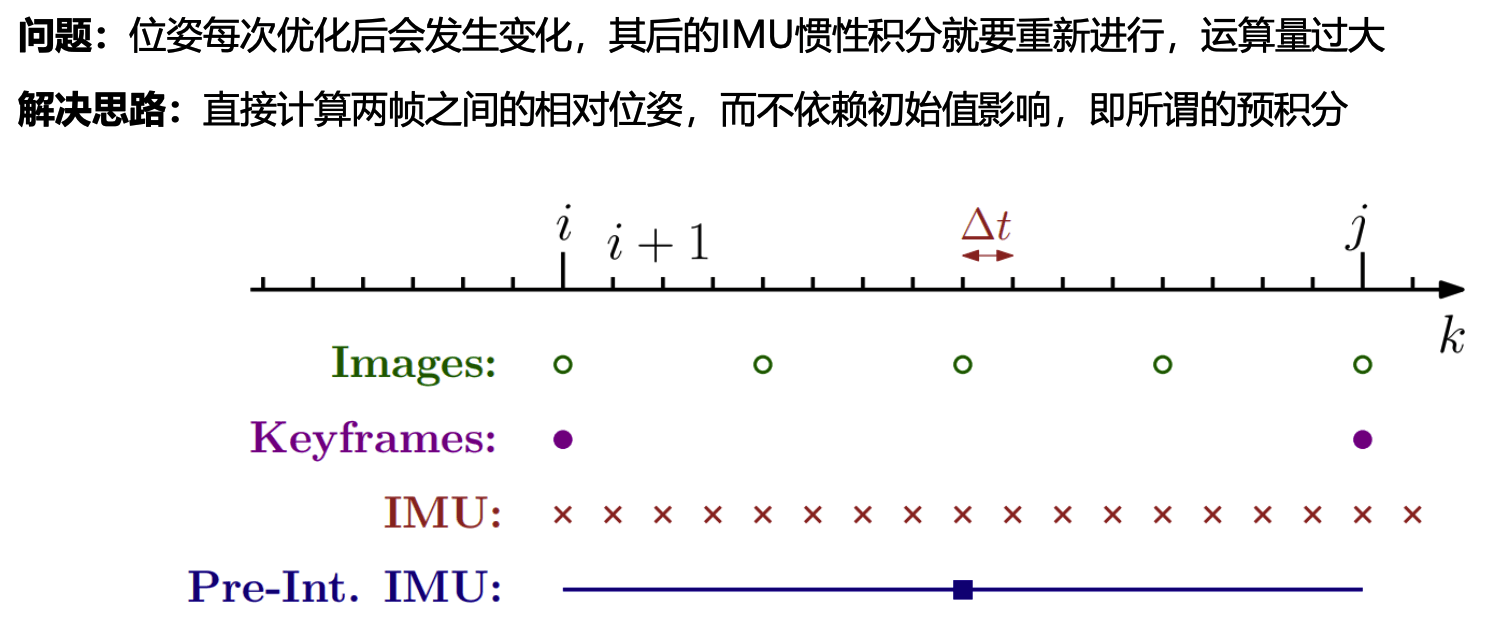
即对两个关键帧之间的imu数据进行整合,得到一个factor,并且该factor基本上不随两个关键帧的状态改变而变化
预积分计算
回顾惯导解算,已知系统位置、速度、姿态的微分方程如下:
\[ \begin{array}{l} \dot{\mathbf{p}}_{w b_{t}}=\mathbf{v}_{t}^{w} \\ \dot{\mathbf{v}}_{t}^{w}=\mathbf{a}_{t}^{w} \\ \dot{\mathbf{q}}_{w b_{t}}=\mathbf{q}_{w b_{t}} \otimes\left[\begin{array}{c} 0 \\ \frac{1}{2} \boldsymbol{\omega}^{b_{t}} \end{array}\right] \end{array} \]
基于上述微分方程,可以得到连续时间下的状态传播方程:
\[ \mathbf{p}_{w b_{j}}= \mathbf{p}_{w b_{i}}+\mathbf{v}_{i}^{w} \Delta t+\iint_{t \in[i, j]}\left(\mathbf{q}_{w b_{t}} \mathbf{a}^{b_{t}}-\mathbf{g}^{w}\right) \delta t^{2} \]
\[ \mathbf{v}_{j}^{w}= \mathbf{v}_{i}^{w}+\int_{t \in[i, j]}\left(\mathbf{q}_{w b_{t}} \mathbf{a}^{b_{t}}-\mathbf{g}^{w}\right) \delta t \]
\[ \mathbf{q}_{w b_{j}}=\int_{t \in[i, j]} \mathbf{q}_{w b_{t}} \otimes\left[\begin{array}{c}0 \\ \frac{1}{2} \boldsymbol{\omega}^{b_{t}}\end{array}\right] \delta t \]
由于上面三个公式都与前一个时刻的状态有关,因此需要进行变换:
根据\(\mathbf{q}_{w b_{t}}=\mathbf{q}_{w b_{i}} \otimes \mathbf{q}_{b_{i} b_{t}}\),即可将上面三个公式中的前一个时刻的位姿项提取出来:
\[ \mathbf{p}_{w b_{j}}=\mathbf{p}_{w b_{i}}+\mathbf{v}_{i}^{w} \Delta t-\frac{1}{2} \mathbf{g}^{w} \Delta t^{2}+\mathbf{q}_{w b_{i}} \underbrace{\iint_{t \in[i, j]}\left(\mathbf{q}_{b_{i} b_{t}} \mathbf{a}^{b_{t}}\right) \delta t^{2}}_{\mathbf{\alpha}} \]
\[ \mathbf{v}_{j}^{w}=\mathbf{v}_{i}^{w}-\mathbf{g}^{w} \Delta t+\mathbf{q}_{w b_{i}}\underbrace{\int_{t \in[i, j]}\left(\mathbf{q}_{b_{i} b_{t}} \mathbf{a}^{b_{t}}\right) \delta t}_{\mathbf{\beta}} \]
\[ \mathbf{q}_{w b_{j}}=\mathbf{q}_{w b_{i}}\underbrace{\int_{t \in[i, j]} \mathbf{q}_{b_{i} b_{t}} \otimes\left[\begin{array}{c}0 \\ \frac{1}{2} \boldsymbol{\omega}^{b_{t}}\end{array}\right] \delta t}_{\mathbf{\gamma}} \]
将上式的积分项分别提取出来,有:
\[ \boldsymbol{\alpha}_{b_{i} b_{j}}=\iint_{t \in[i, j]}\left(\mathbf{q}_{b_{i} b_{t}} \mathbf{a}^{b_{t}}\right) \delta t^{2} \]
\[ \boldsymbol{\beta}_{b_{i} b_{j}}=\int_{t \in[i, j]}\left(\mathbf{q}_{b_{i} b_{t}} \mathbf{a}^{b_{t}}\right) \delta t \]
\[ \mathbf{q}_{b_{i} b_{j}}=\int_{t \in[i, j]} \mathbf{q}_{b_{i} b_{t}} \otimes \left[ \begin{array}{c} 0 \\ \frac{1}{2} \boldsymbol{\omega}^{b_{t}} \end{array} \right] \delta t \]
由于上面的推导都是基于连续时间下的,在实际使用中,通常使用离散形式计算,采用中值积分法:
\[ \boldsymbol{\omega}=\frac{1}{2}\left[\left(\boldsymbol{\omega}^{b_{k}}-\mathbf{b}_{k}^{g}\right)+\left(\boldsymbol{\omega}^{b_{k+1}}-\mathbf{b}_{k}^{g}\right)\right] \]
\[ \mathbf{a}=\frac{1}{2}\left[\mathbf{q}_{b_{i} b_{k}}\left(\mathbf{a}^{b_{k}}-\mathbf{b}_{k}^{a}\right)+\mathbf{q}_{b_{i} b_{k+1}}\left(\mathbf{a}^{b_{k+1}}-\mathbf{b}_{k}^{a}\right)\right] \]
那么预积分量\(\boldsymbol{\alpha}_{b_{i} b_{j}},\boldsymbol{\beta}_{b_{i} b_{j}},\mathbf{q}_{b_{i} b_{j}}\)可以通过迭代计算得到,当新的一帧imu数据到达时,计算该imu预积分的第k+1次迭代,有:
\[ \boldsymbol{\alpha}_{b_{i} b_{k+1}}=\boldsymbol{\alpha}_{b_{i} b_{k}}+\boldsymbol{\beta}_{b_{i} b_{k}} \delta t+\frac{1}{2} \mathbf{a} \delta t^{2} \]
\[ \boldsymbol{\beta}_{b_{i} b_{k+1}}=\boldsymbol{\beta}_{b_{i} b_{k}}+\mathbf{a} \delta t \]
\[ \mathbf{q}_{b_{i} b_{k+1}}=\mathbf{q}_{b_{i} b_{k}} \otimes \left[ \begin{array}{c} 1 \\ \frac{1}{2} \boldsymbol{\omega} \delta t \end{array} \right] \]
预积分量计算完成
基于预积分量的导航状态更新公式为:
\[ \left[ \begin{array}{c} \mathbf{p}_{w b_{j}} \\ \mathbf{v}_{j}^{w} \\ \mathbf{q}_{w b_{j}} \\ \mathbf{b}_{j}^{a} \\ \mathbf{b}_{j}^{g} \end{array} \right] = \left[ \begin{array}{c} \mathbf{p}_{w b_{i}}+\mathbf{v}_{i}^{w} \Delta t-\frac{1}{2} \mathbf{g}^{w} \Delta t^{2}+\mathbf{q}_{w b_{i}} \boldsymbol{\alpha}_{b_{i} b_{j}} \\ \mathbf{v}_{i}^{w}-\mathbf{g}^{w} \Delta t+\mathbf{q}_{w b_{i}} \boldsymbol{\beta}_{b_{i} b_{j}} \\ \mathbf{q}_{w b_{i}} \mathbf{q}_{b_{i} b_{j}} \\ \mathbf{b}_{i}^{a} \\ \mathbf{b}_{i}^{g} \end{array} \right] \]
此中,陀螺仪和加速度计的零偏不变是认为在这个预积分中,由于时间很短,bias基本没有变化。然而,在整个系统中,其实是认为bias在缓慢变化的,因此,陀螺仪加速度计的模型为:
预积分更新
从上面的推导可以发现,预积分量中包含了bias,而在后续的优化过程中,bias作为待优化状态量会随优化而发生改变,因此,预积分量应该随之更新,为了避免完全重新计算预积分,一个技巧是把预积分结果在bias处进行泰勒展开,通过线性近似得到更新的预积分:
\[ \boldsymbol{\alpha}_{b_{i} b_{j}}=\overline{\boldsymbol{\alpha}}_{b_{i} b_{j}}+\mathbf{J}_{b_{i}^{a}}^{\alpha} \boldsymbol{b}_{i}^{a}+\mathbf{J}_{b_{i}^{g}}^{\alpha} \delta \mathbf{b}_{i}^{g} \]
\[ \boldsymbol{\beta}_{b_{i} b_{j}}=\overline{\boldsymbol{\beta}}_{b_{i} b_{j}}+\mathbf{J}_{b_{i}^{a}}^{\beta} \delta \mathbf{b}_{i}^{a}+\mathbf{J}_{b_{i}^{g}}^{\beta} \delta \mathbf{b}_{i}^{g} \]
\[ \mathbf{q}_{b_{i} b_{j}}=\overline{\mathbf{q}}_{b_{i} b_{j}} \otimes \left[ \begin{array}{c} 1 \\ \frac{1}{2} \mathbf{J}_{b_{i}^{g}}^{q} \delta \mathbf{b}_{i}^{g} \end{array} \right] \]
其中,(详细计算见后续)
\[ \begin{aligned} \mathbf{J}_{b_{i}^{a}}^{\alpha} &=\frac{\partial \boldsymbol{\alpha}_{b_{i} b_{j}}}{\partial \delta \mathbf{b}_{i}^{a}} \\ \mathbf{J}_{b_{i}^{g}}^{\alpha} &=\frac{\partial \boldsymbol{\alpha}_{b_{i} b_{j}}}{\partial \delta \mathbf{b}_{i}^{g}} \\ \mathbf{J}_{b_{i}^{a}}^{\beta} &=\frac{\partial \boldsymbol{\beta}_{b_{i} b_{j}}}{\partial \delta \mathbf{b}_{i}^{a}} \\ \mathbf{J}_{b_{i}^{g}}^{\beta} &=\frac{\partial \beta_{b_{i} b_{j}}}{\partial \delta \mathbf{b}_{i}^{g}} \\ \mathbf{J}_{b_{i}^{g}}^{q} &=\frac{\mathbf{q}_{i_{i} b_{j}}}{\partial \mathbf{b}_{i}^{g}} \end{aligned} \]
预积分(误差)协方差计算
由于预积分量是由imu数据迭代计算得到的,然而imu单次测量包含噪声,时间越长,预积分量越不准确,因此,需要计算对应的协方差来表示其不确定性,方差计算公式如下:
\[ \boldsymbol{P}_{i, k+1}=\mathbf{F}_{k} \boldsymbol{P}_{i, k} \mathbf{F}_{k}^{\top}+\mathbf{G}_{k} \boldsymbol{Q} \mathbf{G}_{k}^{\top} \]
注意:上式的\(\mathbf{F}_{k},\mathbf{G}_{k}\)是离散时间下的状态转移矩阵
下面需要求关于预积分误差的微分方程:
已知连续时间下的微分方程形式为:
\[ \dot{\boldsymbol{X}}=\boldsymbol{F}_{t} \boldsymbol{X}+\boldsymbol{G}_{t} \boldsymbol{N} \]
其中,
\[ \boldsymbol{X}= \left[ \begin{array}{l} \delta \boldsymbol{\alpha}_{t}^{b_{k}} \\ \delta \boldsymbol{\theta}_{t}^{b_{k}} \\ \delta \boldsymbol{\beta}_{t}^{b_{k}} \\ \delta \boldsymbol{b}_{a_{t}} \\ \delta \boldsymbol{b}_{w_{t}} \end{array} \right] \]
\[ \boldsymbol{N}= \left[ \begin{array}{l} \boldsymbol{n}_{a} \\ \boldsymbol{n}_{w} \\ \boldsymbol{n}_{b_{a}} \\ \boldsymbol{n}_{b_{w}} \end{array} \right] \]
预积分微分方程
\(\delta \dot{\theta}_t^{b_k}\)微分方程推导
符号简化:\(\delta \dot{\theta}_t^{b_k} \rightarrow \delta \dot \theta\)
此处的\(\boldsymbol{q}_{t}\)就是上面的\(\mathbf{q}_{b_{i} b_{k+1}}\)
- 写出不考虑误差的微分方程
\[ \dot{\boldsymbol{q}}_{t}=\frac{1}{2} \boldsymbol{q}_{t} \otimes \left[ \begin{array}{c} 0 \\ \boldsymbol{\omega}_{t}-\boldsymbol{b}_{\omega_{t}} \end{array} \right] \]
- 写出考虑误差的微分方程
\[ \dot{\tilde{\boldsymbol{q}}}_{t}=\frac{1}{2} \tilde{\boldsymbol{q}}_{t} \otimes \left[ \begin{array}{c} 0 \\ \tilde{\boldsymbol{\omega}}_{t}-\tilde{\boldsymbol{b}}_{\omega_{t}} \end{array} \right] \]
- 写出带有误差的参数与理想真实值之间的关系
\[ \tilde{\boldsymbol{q}}_{t}=\boldsymbol{q}_{t} \otimes \delta \boldsymbol{q} \]
\[ \tilde{\boldsymbol{\omega}}_{t}=\boldsymbol{\omega}_{t}+\boldsymbol{n}_{\omega} \]
\[ \tilde{\boldsymbol{b}}_{\omega_{t}}=\boldsymbol{b}_{\omega_{t}}+\delta \boldsymbol{b}_{\omega_{t}} \]
其中,\(\delta \theta\)是计算坐标系与真实导航坐标系的偏差 或者 在body系与计算误差body系之间的偏差
\[ \delta \boldsymbol{q}= \left[ \begin{array}{c} \cos \left(\frac{|\delta \theta|}{2}\right) \\ \frac{\delta \boldsymbol{\theta}}{|\delta \theta|} \sin \left(\frac{|\delta \theta|}{2}\right) \end{array} \right] \approx \left[ \begin{array}{c} 1 \\ \frac{\delta \boldsymbol{\theta}}{2} \end{array} \right] \]
- 将误差值与理想真实值的关系代入(2)
\[ \left(\boldsymbol{q}_{t} \dot{\otimes} \delta \boldsymbol{q}\right)= \frac{1}{2} \boldsymbol{q}_{t} \otimes \delta \boldsymbol{q} \otimes \left[ \begin{array}{c} 0 \\ \boldsymbol{\omega}_{t}+\boldsymbol{n}_{\omega}-\boldsymbol{b}_{\omega_{t}}-\delta \boldsymbol{b}_{\omega_{t}} \end{array} \right] \]
其中,
\[ \left(\boldsymbol{q}_{t} \dot{\otimes} \delta \boldsymbol{q}\right)=\dot{\boldsymbol{q}}_{t} \otimes \delta \boldsymbol{q}+\boldsymbol{q}_{t} \otimes \delta \dot{\boldsymbol{q}} \]
- 把(1)中的关系代入(4)
\[ \begin{aligned} \left(\boldsymbol{q}_{t} \dot{\otimes} \delta \boldsymbol{q}\right) &= \frac{1}{2} \boldsymbol{q}_{t} \otimes \delta \boldsymbol{q} \otimes\left[\begin{array}{c}0 \\ \boldsymbol{\omega}_{t}+\boldsymbol{n}_{\omega}-\boldsymbol{b}_{\omega_{t}}-\delta \boldsymbol{b}_{\omega_{t}}\end{array}\right] \\ \dot{\boldsymbol{q}}_{t} \otimes \delta \boldsymbol{q}+\boldsymbol{q}_{t} \otimes \delta \boldsymbol{q} &= \\ \frac{1}{2} \boldsymbol{q}_{t} \otimes\left[\begin{array}{c}0 \\ \boldsymbol{\omega}_{t}-\boldsymbol{b}_{\omega_{t}}\end{array}\right] \otimes \delta \boldsymbol{q}+\boldsymbol{q}_{t} \otimes \dot{\delta \boldsymbol{q}} &= \end{aligned} \]
- 化简
(5)两边同时左乘\((\boldsymbol{q}_t)^{-1}\),然后移项得到:
\[ \delta \dot{\boldsymbol{q}}= \frac{1}{2} \delta \boldsymbol{q} \otimes \left[ \begin{array}{c} 0 \\ \boldsymbol{\omega}_{t}+\boldsymbol{n}_{\omega}-\boldsymbol{b}_{\omega_{t}}-\delta \boldsymbol{b}_{\omega_{t}} \end{array} \right] -\frac{1}{2} \left[ \begin{array}{c} 0 \\ \boldsymbol{\omega}_{t}-\boldsymbol{b}_{\omega_{t}} \end{array} \right] \otimes \delta \boldsymbol{q} \]
根据四元数乘法性质,可以将四元数乘法转换成矩阵与向量相乘:
因此,可得:
\[ \begin{aligned} \delta \dot{\boldsymbol{q}} &= \frac{1}{2} \left[ \begin{array}{c}0 \\ \boldsymbol{\omega}_{1} \end{array} \right]_{R} \delta \boldsymbol{q} - \frac{1}{2} \left[ \begin{array}{c}0 \\ \boldsymbol{\omega}_{2} \end{array} \right]_{L} \delta \boldsymbol{q} \\ &= \frac{1}{2} \left[ \begin{array}{cc} 0 & \left(\boldsymbol{\omega}_{2}-\boldsymbol{\omega}_{1}\right)^{T} \\ \left(\boldsymbol{\omega}_{1}-\boldsymbol{\omega}_{2}\right) & -\left[\boldsymbol{\omega}_{1}+\boldsymbol{\omega}_{2}\right]_{\times} \end{array} \right] \delta \boldsymbol{q} \end{aligned} \]
其中,
\[ \boldsymbol{\omega}_{1}=\boldsymbol{\omega}_{t}+\boldsymbol{n}_{\omega}-\boldsymbol{b}_{\omega_{t}}-\delta \boldsymbol{b}_{\omega_{t}} \]
\[\boldsymbol{\omega}_{2}=\boldsymbol{\omega}_{t}-\boldsymbol{b}_{\omega_{t}}\]
又因为:
\[\delta \dot{\boldsymbol{q}}= \left[ \begin{array}{l} 0 \\ \frac{\delta \dot{\theta}}{2} \end{array} \right] \]
可以得到关于\(\delta \dot{\theta}\)的方程:
\[ \begin{aligned} \delta \dot{\boldsymbol{\theta}} &= -\left[\boldsymbol{\omega}_{1}+\boldsymbol{\omega}_{2}\right] \times \frac{\delta \boldsymbol{\theta}}{2}+\left(\boldsymbol{\omega}_{1}-\boldsymbol{\omega}_{2}\right) \\ &= -\left[2 \boldsymbol{\omega}_{t}+\boldsymbol{n}_{\omega}-2 \boldsymbol{b}_{\omega_{t}}-\delta \boldsymbol{b}_{\omega_{t}}\right]_\times \frac{\delta \boldsymbol{\theta}}{2}+\boldsymbol{n}_{\omega}-\delta \boldsymbol{b}_{\omega_{t}} \end{aligned} \]
忽略上式中的二阶小项,可得\(\delta \dot{\theta}_t^{b_k}\)微分方程
\[ \delta \dot{\boldsymbol{\theta}}=-\left[\boldsymbol{\omega}_{t}-\boldsymbol{b}_{\omega_{t}}\right]_{\times} \delta \boldsymbol{\theta}+\boldsymbol{n}_{\omega}-\delta \boldsymbol{b}_{\omega_{t}} \]
\(\delta \dot{\beta}_t^{b_k}\)微分方程推导
符号简化:\(\delta \dot{\beta}_t^{b_k} \rightarrow \delta \dot \beta\),此处的\(\boldsymbol{\beta}\)就是上面的\(\boldsymbol{\beta}_{b_{i} b_{k+1}}\)
- 写出不考虑误差的微分方程
\[ \dot{\boldsymbol{\beta}}=\boldsymbol{R}_{t}\left(\boldsymbol{a}_{t}-\boldsymbol{b}_{a_{t}}\right) \]
其中,\(\boldsymbol{R}_{t}\)表示载体姿态
- 写出考虑误差的微分方程
\[ \dot{\tilde{\boldsymbol{\beta}}}=\tilde{\boldsymbol{R}}_{t}\left(\tilde{\boldsymbol{a}}_{t}-\tilde{\boldsymbol{b}}_{a_{t}}\right) \]
- 写出带有误差的参数与理想真实值之间的关系
\[\tilde{\boldsymbol{\beta}}=\boldsymbol{\beta}+\delta \boldsymbol{\beta}\]
\[\tilde{\boldsymbol{a}}_{t}=\boldsymbol{a}_{t}+\boldsymbol{n}_{a}\]
\[\tilde{\boldsymbol{b}}_{a_{t}}=\boldsymbol{b}_{a_{t}}+\delta \boldsymbol{b}_{a_{t}}\]
\[ \begin{aligned} \tilde{\boldsymbol{R}}_{t} &=\boldsymbol{R}_{t} \exp \left([\delta \boldsymbol{\theta}]_{\times}\right) \\ &=\boldsymbol{R}_{t}\left(\boldsymbol{I}+[\delta \boldsymbol{\theta}]_{\times}\right) \end{aligned} \]
关于姿态与理想真实值的关系: 因为 \(\delta \boldsymbol{\theta}\)表示的是在载体姿态上的误差,直接右乘即可
- 将误差值与理想真实值的关系代入(2)
\[ \begin{aligned} & \dot{\boldsymbol{\beta}}+\delta \dot{\boldsymbol{\beta}} \\ =& \boldsymbol{R}_{t}\left(\boldsymbol{I}+[\delta \boldsymbol{\theta}]_{\times}\right)\left(\boldsymbol{a}_{t}+\boldsymbol{n}_{a}-\boldsymbol{b}_{a_{t}}-\delta \boldsymbol{b}_{a_{t}}\right) \end{aligned} \]
- 把(1)中的关系代入(4)
\[ \begin{aligned} & \boldsymbol{R}_{t}\left(\boldsymbol{a}_{t}-\boldsymbol{b}_{a_{t}}\right)+\delta \boldsymbol{\beta} \\ =& \boldsymbol{R}_{t}\left(\boldsymbol{I}+[\delta \boldsymbol{\theta}]_{\times}\right)\left(\boldsymbol{a}_{t}+\boldsymbol{n}_{a}-\boldsymbol{b}_{a_{t}}-\delta \boldsymbol{b}_{a_{t}}\right) \end{aligned} \]
- 化简(忽略二阶小项)
\[ \begin{aligned} & \delta \dot{\boldsymbol{\beta}} \\ =& \boldsymbol{R}_{t}[\delta \boldsymbol{\theta}]_{\times}\left(\boldsymbol{a}_{t}-\boldsymbol{b}_{a_{t}}\right)+\boldsymbol{R}_{t}\left(\boldsymbol{n}_{a}-\delta \boldsymbol{b}_{a_{t}}\right) \\ =&-\boldsymbol{R}_{t}\left[\boldsymbol{a}_{t}-\boldsymbol{b}_{a_{t}}\right]_{\times} \delta \boldsymbol{\theta}+\boldsymbol{R}_{t}\left(\boldsymbol{n}_{a}-\delta \boldsymbol{b}_{a_{t}}\right) \end{aligned} \]
\(\delta \dot{\alpha}_t^{b_k}\)微分方程推导
符号简化:\(\delta \dot{\alpha}_t^{b_k} \rightarrow \delta \dot \alpha\)
- 写出不考虑误差的微分方程
\[ \dot{\alpha}=\boldsymbol{\beta} \]
- 写出考虑误差的微分方程
\[ \dot{\tilde{\boldsymbol{\alpha}}}=\tilde{\boldsymbol{\beta}} \]
- 写出带有误差的参数与理想真实值之间的关系
\[ \begin{aligned} \tilde \alpha = \alpha + \delta \alpha \\ \tilde \beta = \beta + \delta \beta \end{aligned} \]
- 将误差值与理想真实值的关系代入(2)
\[ \begin{aligned} \dot {(\alpha + \delta \alpha)} = \beta + \delta \beta \\ \dot {\alpha} + \dot{\delta \alpha} = \beta + \delta \beta \end{aligned} \]
- 把(1)中的关系代入(4)
\[ \boldsymbol{\beta}+\delta \dot{\boldsymbol{\alpha}}=\boldsymbol{\beta}+\delta \boldsymbol{\beta} \]
- 化简
\[ \delta \dot{\boldsymbol{\alpha}}=\delta \boldsymbol{\beta} \]
预积分离散时间递推方程
实际上,计算预积分的方差,还需要离散时间下的递推方程,因此,需要对上面求出来的连续时间微分方程进行离散化,即:
已知连续时间下的微分方程形式为:
\[ \dot{\boldsymbol{X}}=\boldsymbol{F}_{t} \boldsymbol{X}+\boldsymbol{G}_{t} \boldsymbol{N} \]
离散化后的递推方程形式为:
\[ \boldsymbol{X}_{k+1}=\boldsymbol{F}_{k} \boldsymbol{X}_{k}+\boldsymbol{G}_{k} \boldsymbol{N}_{k} \]
其中,
\[ \boldsymbol{X}_{k+1}=\left[\begin{array}{c} \delta \boldsymbol{\alpha}_{k+1} \\ \delta \boldsymbol{\theta}_{k+1} \\ \delta \boldsymbol{\beta}_{k+1} \\ \delta \boldsymbol{b}_{a_{k+1}} \\ \delta \boldsymbol{b}_{\omega_{k+1}} \end{array}\right] \quad \boldsymbol{X}_{k}=\left[\begin{array}{c} \delta \boldsymbol{\alpha}_{k} \\ \delta \boldsymbol{\theta}_{k} \\ \delta \boldsymbol{\beta}_{k} \\ \delta \boldsymbol{b}_{a_{k}} \\ \delta \boldsymbol{b}_{\omega_{k}} \end{array}\right] \quad \boldsymbol{N}_{k}=\left[\begin{array}{c} \boldsymbol{n}_{a_{k}} \\ \boldsymbol{n}_{w_{k}} \\ \boldsymbol{n}_{a_{k+1}} \\ \boldsymbol{n}_{w_{k+1}} \\ \boldsymbol{n}_{b_{a}} \\ \boldsymbol{n}_{b_{w}} \end{array}\right] \]
more detail:


\(\delta \boldsymbol{\theta}_{k+1}\)递推
这里直接写出上面推导的微分方程:
\[ \delta \dot{\boldsymbol{\theta}}=-\left[\boldsymbol{\omega}_{t}-\boldsymbol{b}_{\omega_{t}}\right]_{\times} \delta \boldsymbol{\theta}+\boldsymbol{n}_{\omega}-\delta \boldsymbol{b}_{\omega_{t}} \]
改写成中值积分法:
\[ \delta \dot{\boldsymbol{\theta}}_{k}=-\left[\frac{\boldsymbol{\omega}_{k}+\boldsymbol{\omega}_{k+1}}{2}-\boldsymbol{b}_{\omega_{t}}\right]_{\times} \delta \boldsymbol{\theta}_{k}+\boldsymbol{n}_{\omega}-\delta \boldsymbol{b}_{\omega_{t}} \]
因此,离散时间下,有:
\[ \begin{aligned} \delta \boldsymbol{\theta}_{k+1}&= \delta \boldsymbol{\theta}_{k} + \left ( -\left[\frac{\boldsymbol{\omega}_{k}+\boldsymbol{\omega}_{k+1}}{2}-\boldsymbol{b}_{\omega_{t}}\right]_{\times} \delta \boldsymbol{\theta}_{k}+\boldsymbol{n}_{\omega}-\delta \boldsymbol{b}_{\omega_{t}} \right) \delta t \\ &=\left[\boldsymbol{I}-\left[\frac{\boldsymbol{\omega}_{k}+\boldsymbol{\omega}_{k+1}}{2}-\boldsymbol{b}_{\omega_{k}}\right]_{\times} \delta t\right] \delta \boldsymbol{\theta}_{k}+\delta t \frac{\boldsymbol{n}_{\omega_{k}}+\boldsymbol{n}_{\omega_{k+1}}}{2}-\delta t \delta \boldsymbol{b}_{\omega_{k}} \end{aligned} \]
令: \(\overline{\boldsymbol{\omega}}=\frac{\boldsymbol{\omega}_{k}+\boldsymbol{\omega}_{k+1}}{2}-\boldsymbol{b}_{\omega_{k}}\),则上式可重写为:
\[ \delta \boldsymbol{\theta}_{k+1}=\left[\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right] \delta \boldsymbol{\theta}_{k}+\frac{\delta t}{2} \boldsymbol{n}_{\omega_{k}}+\frac{\delta t}{2} \boldsymbol{n}_{\omega_{k+1}}-\delta t \delta \boldsymbol{b}_{\omega_{k}} \]
\(\delta \boldsymbol{\beta}_{k+1}\)递推
这里直接写出上面推导的微分方程,即连续时间下,有:
\[ \delta \dot{\boldsymbol{\beta}}=-\boldsymbol{R}_{t}\left[\boldsymbol{a}_{t}-\boldsymbol{b}_{a_{t}}\right]_{\times} \delta \boldsymbol{\theta}+\boldsymbol{R}_{t}\left(\boldsymbol{n}_{a}-\delta \boldsymbol{b}_{a_{t}}\right) \]
改成中值积分法形式,有:
\[ \begin{aligned} \delta \dot{\boldsymbol{\beta}}_{k}=&-\frac{1}{2} \boldsymbol{R}_{k}\left[\boldsymbol{a}_{k}-\boldsymbol{b}_{a_{k}}\right]_{\times} \delta \boldsymbol{\theta}_{k} \\ &-\frac{1}{2} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \delta \boldsymbol{\theta}_{k+1} \\ &+\frac{1}{2} \boldsymbol{R}_{k} \boldsymbol{n}_{a_{k}} +\frac{1}{2} \boldsymbol{R}_{k+1} \boldsymbol{n}_{a_{k+1}} \\ &-\frac{1}{2}\left(\boldsymbol{R}_{k}+\boldsymbol{R}_{k+1}\right) \delta \boldsymbol{b}_{a_{k}} \end{aligned} \]
根据上述\(\delta \boldsymbol{\beta}_{k+1}\)递推的结果,\(\delta \boldsymbol{\theta}_{k+1}\)如下:
\[ \delta \boldsymbol{\theta}_{k+1}=\left[\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right] \delta \boldsymbol{\theta}_{k}+\frac{\delta t}{2} \boldsymbol{n}_{\omega_{k}}+\frac{\delta t}{2} \boldsymbol{n}_{\omega_{k+1}}-\delta t \delta \boldsymbol{b}_{\omega_{k}} \]
其中,\(\overline{\boldsymbol{\omega}}=\frac{\boldsymbol{\omega}_{k}+\boldsymbol{\omega}_{k+1}}{2}-\boldsymbol{b}_{\omega_{k}}\)
将\(\delta \boldsymbol{\theta}_{k+1}\)代入到\(\delta \dot{\boldsymbol{\beta}}_{k}\),可得:
\[ \begin{aligned} \delta \dot{\boldsymbol{\beta}}_{k}=&-\frac{1}{2} \boldsymbol{R}_{k}\left[\boldsymbol{a}_{k}-\boldsymbol{b}_{a_{k}}\right]_{\times} \delta \boldsymbol{\theta}_{k} \\ &-\frac{1}{2} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times}\left\{\left[\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right] \delta \boldsymbol{\theta}_{k}+\frac{\delta t}{2} \boldsymbol{n}_{\omega_{k}}+\frac{\delta t}{2} \boldsymbol{n}_{\omega_{k+1}}-\delta t \delta \boldsymbol{b}_{\omega_{k}}\right\} \\ &+\frac{1}{2} \boldsymbol{R}_{k} \boldsymbol{n}_{a_{k}} +\frac{1}{2} \boldsymbol{R}_{k+1} \boldsymbol{n}_{a_{k+1}} \\ &-\frac{1}{2}\left(\boldsymbol{R}_{k}+\boldsymbol{R}_{k+1}\right) \delta \boldsymbol{b}_{a_{k}} \end{aligned} \]
进一步化简,合并同类项,可以得到微分方程中间结果:
\[ \begin{aligned} \delta \dot{\boldsymbol{\beta}}_{k}=&-\frac{1}{2}\left[\boldsymbol{R}_{k}\left[\boldsymbol{a}_{k}-\boldsymbol{b}_{a_{k}}\right]_{\times}+\boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times}\left(\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right)\right] \delta \boldsymbol{\theta}_{k} \\ &-\frac{\delta t}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \boldsymbol{n}_{\omega_{k}} \\ &-\frac{\delta t}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \boldsymbol{n}_{\omega_{k+1}} \\ &+\frac{\delta t}{2} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \delta \boldsymbol{b}_{\omega_{k}} \\ &+\frac{1}{2} \boldsymbol{R}_{k} \boldsymbol{n}_{a_{k}} \\ &+\frac{1}{2} \boldsymbol{R}_{k+1} \boldsymbol{n}_{a_{k+1}} \\ &-\frac{1}{2}\left(\boldsymbol{R}_{k}+\boldsymbol{R}_{k+1}\right) \delta \boldsymbol{b}_{a_{k}} \end{aligned} \]
对\(\delta t\)进行积分,即由导数形式可以得到递推形式如下:
\[ \begin{aligned} \delta \boldsymbol{\beta}_{k+1} = & \enspace \delta \boldsymbol{\beta}_{k} + \delta \dot{\boldsymbol{\beta}}_{k} \delta t \\ =& \enspace \delta \boldsymbol{\beta}_{k} \\ &-\frac{\delta t}{2}\left[\boldsymbol{R}_{k}\left[\boldsymbol{a}_{k}-\boldsymbol{b}_{a_{k}}\right]_{\times}+\boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times}\left(\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right)\right] \delta \boldsymbol{\theta}_{k} \\ &-\frac{\delta t^{2}}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \boldsymbol{n}_{\omega_{k}} \\ &-\frac{\delta t^{2}}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \boldsymbol{n}_{\omega_{k+1}} \\ &+\frac{\delta t^{2}}{2} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \delta \boldsymbol{b}_{\omega_{k}} \\ &+\frac{\delta t}{2} \boldsymbol{R}_{k} \boldsymbol{n}_{a_{k}} \\ &+\frac{\delta t}{2} \boldsymbol{R}_{k+1} \boldsymbol{n}_{a_{k+1}} \\ &-\frac{\delta t}{2}\left(\boldsymbol{R}_{k}+\boldsymbol{R}_{k+1}\right) \delta \boldsymbol{b}_{a_{k}} \end{aligned} \]
\(\delta \boldsymbol{\alpha}_{k+1}\)递推
这里直接写出上面推导的微分方程,即连续时间下,有:
\[ \delta \dot{\boldsymbol{\alpha}}=\delta \boldsymbol{\beta} \]
改成中值积分法形式,有:
\[ \delta \dot{\boldsymbol{\alpha}}_{k}=\frac{1}{2} \delta \boldsymbol{\beta}_{k}+\frac{1}{2} \delta \boldsymbol{\beta}_{k+1} \]
将\(\delta \boldsymbol{\beta}_{k+1}\)的递推结果代入到可得:
\[ \begin{aligned} \delta \dot{\boldsymbol{\alpha}}_{k}=& \frac{1}{2} \delta \boldsymbol{\beta}_{k}+\frac{1}{2} \delta \boldsymbol{\beta}_{k+1} \\ =& \enspace \delta \boldsymbol{\beta}_{k} \\ &-\frac{\delta t}{4}\left[\boldsymbol{R}_{k}\left[\boldsymbol{a}_{k}-\boldsymbol{b}_{a_{k}}\right]_{\times}+\boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times}\left(\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right)\right] \delta \boldsymbol{\theta}_{k} \\ &-\frac{\delta t^{2}}{8} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \boldsymbol{n}_{\omega_{k}} \\ &-\frac{\delta t^{2}}{8} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \boldsymbol{n}_{\omega_{k+1}} \\ &+\frac{\delta t^{2}}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \delta \boldsymbol{b}_{\omega_{k}} \\ &+\frac{\delta t}{4} \boldsymbol{R}_{k} \boldsymbol{n}_{a_{k}} \\ &+\frac{\delta t}{4} \boldsymbol{R}_{k+1} \boldsymbol{n}_{a_{k+1}} \\ &-\frac{\delta t}{4}\left(\boldsymbol{R}_{k}+\boldsymbol{R}_{k+1}\right) \delta \boldsymbol{b}_{a_{k}} \end{aligned} \]
对\(\delta t\)进行积分,即由导数形式可以得到递推形式如下:
\[ \begin{aligned} \delta \boldsymbol{\alpha}_{k+1}= & \enspace \delta \boldsymbol{\alpha}_{k} + \delta \dot{\boldsymbol{\alpha}}_{k} \delta t \\ =& \enspace \delta \boldsymbol{\alpha}_{k} +\delta t \delta \boldsymbol{\beta}_{k} \\ &-\frac{\delta t^{2}}{4}\left[\boldsymbol{R}_{k}\left[\boldsymbol{a}_{k}-\boldsymbol{b}_{a_{k}}\right]_{\times}+\boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times}\left(\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right)\right] \delta \boldsymbol{\theta}_{k} \\ &-\frac{\delta t^{3}}{8} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \boldsymbol{n}_{\omega_{k}} \\ &-\frac{\delta t^{3}}{8} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \boldsymbol{n}_{\omega_{k+1}} \\ &+\frac{\delta t^{3}}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \delta \boldsymbol{b}_{\omega_{k}} \\ &+\frac{\delta t^{2}}{4} \boldsymbol{R}_{k} \boldsymbol{n}_{a_{k}} \\ &+\frac{\delta t^{2}}{4} \boldsymbol{R}_{k+1} \boldsymbol{n}_{a_{k+1}} \\ &-\frac{\delta t^{2}}{4}\left(\boldsymbol{R}_{k}+\boldsymbol{R}_{k+1}\right) \delta \boldsymbol{b}_{a_{k}} \end{aligned} \]
预积分方差计算
由上面的离散时间下的递推方程,可以写出预积分离散时间的状态方程:
\[ \boldsymbol{X}_{k+1}=\boldsymbol{F}_{k} \boldsymbol{X}_{k}+\boldsymbol{G}_{k} \boldsymbol{N}_{k} \]
其中\(\mathbf{F}_{k}\)如下,
\[ \mathbf{F}_{k}=\left[\begin{array}{ccccc} \mathbf{I} & \mathbf{f}_{12} & \mathbf{I} \delta t & -\frac{1}{4}\left(\boldsymbol{R}_{k}+\boldsymbol{R}_{k+1}\right) \delta t^{2} & \mathbf{f}_{15} \\ \mathbf{0} & \mathbf{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t & \mathbf{0} & \mathbf{0} & -\mathbf{I} \delta t \\ \mathbf{0} & \mathbf{f}_{32} & \mathbf{I} & -\frac{1}{2}\left(\boldsymbol{R}_{k}+\boldsymbol{R}_{k+1}\right) \delta t & \mathbf{f}_{35} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} \end{array}\right] \]
且:
\[ \begin{aligned} &\boldsymbol{f}_{12}=-\frac{\delta t^{2}}{4}\left[\boldsymbol{R}_{k}\left[\boldsymbol{a}_{k}-\boldsymbol{b}_{a_{k}}\right]_{\times}+\boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times}\left(\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right)\right] \\ &\boldsymbol{f}_{15}=\frac{\delta t^{3}}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \delta \boldsymbol{b}_{\omega_{k}} \\ &\boldsymbol{f}_{32}=-\frac{\delta t}{2}\left[\boldsymbol{R}_{k}\left[\boldsymbol{a}_{k}-\boldsymbol{b}_{a_{k}}\right]_{\times}+\boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times}\left(\boldsymbol{I}-[\overline{\boldsymbol{\omega}}]_{\times} \delta t\right)\right] \\ &\boldsymbol{f}_{35}=\frac{\delta t^{2}}{2} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \end{aligned} \]
其中\(\mathbf{G}_{k}\)如下,
\[ \mathbf{G}_{k}=\left[\begin{array}{cccccc} \frac{1}{4} \boldsymbol{R}_{k} \delta t^{2} & \mathbf{g}_{12} & \frac{1}{4} \boldsymbol{R}_{k+1} \delta t^{2} & \mathbf{g}_{14} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \frac{1}{2} \mathbf{I} \delta t & \mathbf{0} & \frac{1}{2} \mathbf{I} \delta t & \mathbf{0} & \mathbf{0} \\ \frac{1}{2} \boldsymbol{R}_{k} \delta t & \mathbf{g}_{32} & \frac{1}{2} \boldsymbol{R}_{k+1} \delta t & \mathbf{g}_{34} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} \delta t & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} \delta t \end{array}\right] \]
且:
\[ \begin{aligned} &\boldsymbol{g}_{12}=-\frac{\delta t^{3}}{8} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \\ &\boldsymbol{g}_{14}=-\frac{\delta t^{3}}{8} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \\ &\boldsymbol{g}_{32}=-\frac{\delta t^{2}}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \\ &\boldsymbol{g}_{34}=-\frac{\delta t^{2}}{4} \boldsymbol{R}_{k+1}\left[\boldsymbol{a}_{k+1}-\boldsymbol{b}_{a_{k}}\right]_{\times} \end{aligned} \]
需要注意的是,上面的\(\boldsymbol{R}_{k}, \boldsymbol{R}_{k+1}\)都是相对于这个imu预积分起始时刻的,即\(\boldsymbol{R}_{k} = \mathbf{R}_{b_{i} b_{k}}, \quad \boldsymbol{R}_{k+1} = \mathbf{R}_{b_{i} b_{k+1}}\)
计算得到矩阵\(\mathbf{F}_{k}\)和\(\mathbf{G}_{k}\)后,即可按照如下公式来计算方差:
\[ \boldsymbol{P}_{i, k+1}=\mathbf{F}_{k} \boldsymbol{P}_{i, k} \mathbf{F}_{k}^{\top}+\mathbf{G}_{k} \boldsymbol{Q} \mathbf{G}_{k}^{\top} \]
预积分残差关于待求状态量的雅可比
在优化时,需要求出残差对待求解的状态量的雅可比。
已知基于预积分量的状态更新如下:
\[ \left[\begin{array}{c} \mathbf{p}_{w b_{j}} \\ \mathbf{q}_{w b_{j}} \\ \mathbf{v}_{j}^{w} \\ \mathbf{b}_{j}^{a} \\ \mathbf{b}_{j}^{g} \end{array}\right]=\left[\begin{array}{c} \mathbf{p}_{w b_{i}}+\mathbf{v}_{i}^{w} \Delta t-\frac{1}{2} \mathbf{g}^{w} \Delta t^{2}+\mathbf{q}_{w b_{i}} \boldsymbol{\alpha}_{b_{i} b_{j}} \\ \mathbf{q}_{w b_{i}} \mathbf{q}_{b_{i} b_{j}} \\ \mathbf{v}_{i}^{w}-\mathbf{g}^{w} \Delta t+\mathbf{q}_{w b_{i}} \boldsymbol{\beta}_{b_{i} b_{j}} \\ \mathbf{b}_{i}^{a} \\ \mathbf{b}_{i}^{g} \end{array}\right] \]
把上式左侧状态移到右侧,在理想的情况下左侧应该只剩下0,但是由于误差的存在,可以使用残差小量\(\mathbf{r}\)代替,因此有:
\[ \left[\begin{array}{c} \mathbf{r}_{p} \\ \mathbf{r}_{q} \\ \mathbf{r}_{v} \\ \mathbf{r}_{b a} \\ \mathbf{r}_{b g} \end{array}\right]=\left[\begin{array}{c} \mathbf{p}_{w b_{j}}-\mathbf{p}_{w b_{i}}-\mathbf{v}_{i}^{w} \Delta t+\frac{1}{2} \mathbf{g}^{w} \Delta t^{2}-\mathbf{q}_{w b_{i}} \boldsymbol{\alpha}_{b_{i} b_{j}} \\ 2\left[\mathbf{q}_{b_{i} b_{j}}^{*} \otimes\left(\mathbf{q}_{w b_{i}}^{*} \otimes \mathbf{q}_{w b_{j}}\right)\right]_{x y z} \\ \mathbf{v}_{j}^{w}-\mathbf{v}_{i}^{w}+\mathbf{g}^{w} \Delta t-\mathbf{q}_{w b_{i}} \boldsymbol{\beta}_{b_{i} b_{j}} \\ \mathbf{b}_{j}^{a}-\mathbf{b}_{i}^{a} \\ \mathbf{b}_{j}^{g}-\mathbf{b}_{i}^{g} \end{array}\right] \]
其中,关于姿态残差\(\mathbf{r}_{q}\)部分,需要将四元数拆开来看,根据四元数与等轴旋转矢量\(\mathbf{\phi}\)的关系:
\[ \mathbf{q}=\cos \frac{\phi}{2}+\left(u_{x} i+u_{y} j+u_{z} k\right) \sin \frac{\phi}{2}=\left[\begin{array}{c} \cos (\phi / 2) \\ \mathbf{u} \sin (\phi / 2) \end{array}\right] \]
等效旋转矢量可以用向量\(\mathbf{\phi}\),并用单位向量\(\mathbf{u}\)表示它的朝向,\(\phi\)表示它的大小,因此有: \(\mathbf{\phi}=\phi \boldsymbol{u}\)
其中,
\[ \mathbf{r}_{q} = 2\left[\mathbf{q}_{b_{i} b_{j}}^{*} \otimes\left(\mathbf{q}_{w b_{i}}^{*} \otimes \mathbf{q}_{w b_{j}}\right)\right]_{x y z} \]
取\([]_{xyz}\)就是取四元数的虚部\(\mathbf{u} \sin (\phi / 2)\),特别的,当旋转角度\(\phi\)是小量时,\(\sin (\phi / 2) \approx \phi / 2\),对其乘个2,就得到了上面的姿态残差\(\mathbf{r}_{q}\)。
在上面的预积分误差中,和预积分相关的量,仍然与上一时刻的姿态有关,如\(\mathbf{r}_{p},\mathbf{r}_{v}\),无法直接加减(啥意思),因此,把预积分残差进行修正,得到:
\[ \left[\begin{array}{c} \mathbf{r}_{p} \\ \mathbf{r}_{q} \\ \mathbf{r}_{v} \\ \mathbf{r}_{b a} \\ \mathbf{r}_{b g} \end{array}\right]=\left[\begin{array}{c} \mathbf{q}_{w b_{i}}^{*}\left(\mathbf{p}_{w b_{j}}-\mathbf{p}_{w b_{i}}-\mathbf{v}_{i}^{w} \Delta t+\frac{1}{2} \mathbf{g}^{w} \Delta t^{2}\right)-\boldsymbol{\alpha}_{b_{i} b_{j}} \\ 2\left[\mathbf{q}_{b_{i} b_{j}}^{*} \otimes\left(\mathbf{q}_{w b_{i}}^{*} \otimes \mathbf{q}_{w b_{j}}\right)\right]_{x y z} \\ \mathbf{q}_{w b_{i}}^{*}\left(\mathbf{v}_{j}^{w}-\mathbf{v}_{i}^{w}+\mathbf{g}^{w} \Delta t\right)-\boldsymbol{\beta}_{b_{i} b_{j}} \\ \mathbf{b}_{j}^{a}-\mathbf{b}_{i}^{a} \\ \mathbf{b}_{j}^{g}-\mathbf{b}_{i}^{g} \end{array}\right] \]
其中,待优化的变量是前后两帧的状态量:
\[ \left[\begin{array}{lllll} \mathbf{p}_{w b_{i}} & \mathbf{q}_{w b_{i}} & \mathbf{v}_{i}^{w} & \mathbf{b}_{i}^{a} & \mathbf{b}_{i}^{g} \end{array}\right] \]
\[ \left[\begin{array}{lllll} \mathbf{p}_{w b_{j}} & \mathbf{q}_{w b_{j}} & \mathbf{v}_{j}^{w} & \mathbf{b}_{j}^{a} & \mathbf{b}_{j}^{g} \end{array}\right] \]
而实际上,求导使用了扰动量,即实际上是对以下扰动量求雅可比:
\[ \left[\begin{array}{lllll} \delta \mathbf{p}_{w b_{i}} & \delta \theta_{w b_{i}} & \delta \mathbf{v}_{i}^{w} & \delta \mathbf{b}_{i}^{a} & \delta \mathbf{b}_{i}^{g} \end{array}\right] \]
\[ \left[\begin{array}{lllll} \delta \mathbf{p}_{w b_{j}} & \delta \theta_{w b_{j}} & \delta \mathbf{v}_{j}^{w} & \delta \mathbf{b}_{j}^{a} & \delta \mathbf{b}_{j}^{g} \end{array}\right] \]
\(\mathbf{r}_{p}\)对状态量的雅可比
首先,直接写出残差:
\[ \mathbf{r}_{p} = \mathbf{q}_{w b_{i}}^{*}\left(\mathbf{p}_{w b_{j}}-\mathbf{p}_{w b_{i}}-\mathbf{v}_{i}^{w} \Delta t+\frac{1}{2} \mathbf{g}^{w} \Delta t^{2}\right)-\boldsymbol{\alpha}_{b_{i} b_{j}} \]
对状态i求雅可比
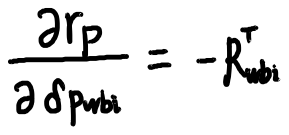

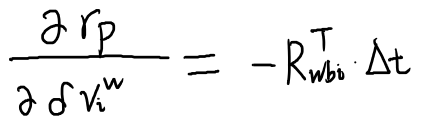
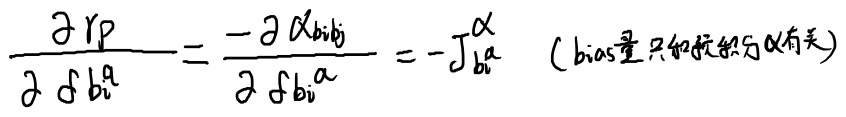
对状态j求雅可比
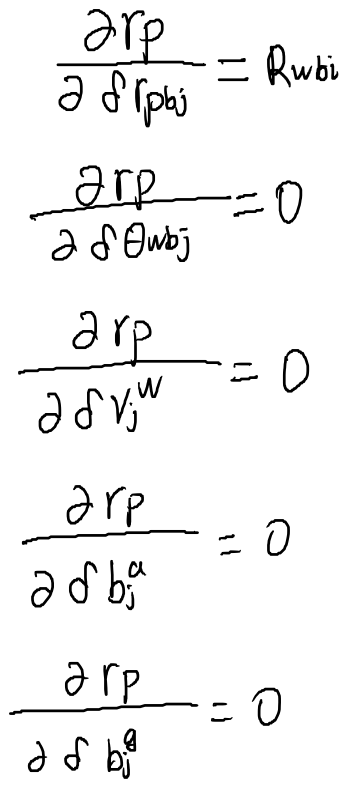
\(\mathbf{r}_{q}\)对状态量的雅可比
首先,直接写出残差:
\[ \mathbf{r}_{q} = 2\left[\mathbf{q}_{b_{i} b_{j}}^{*} \otimes\left(\mathbf{q}_{w b_{i}}^{*} \otimes \mathbf{q}_{w b_{j}}\right)\right]_{x y z} \]
对状态i求雅可比

对状态j求雅可比
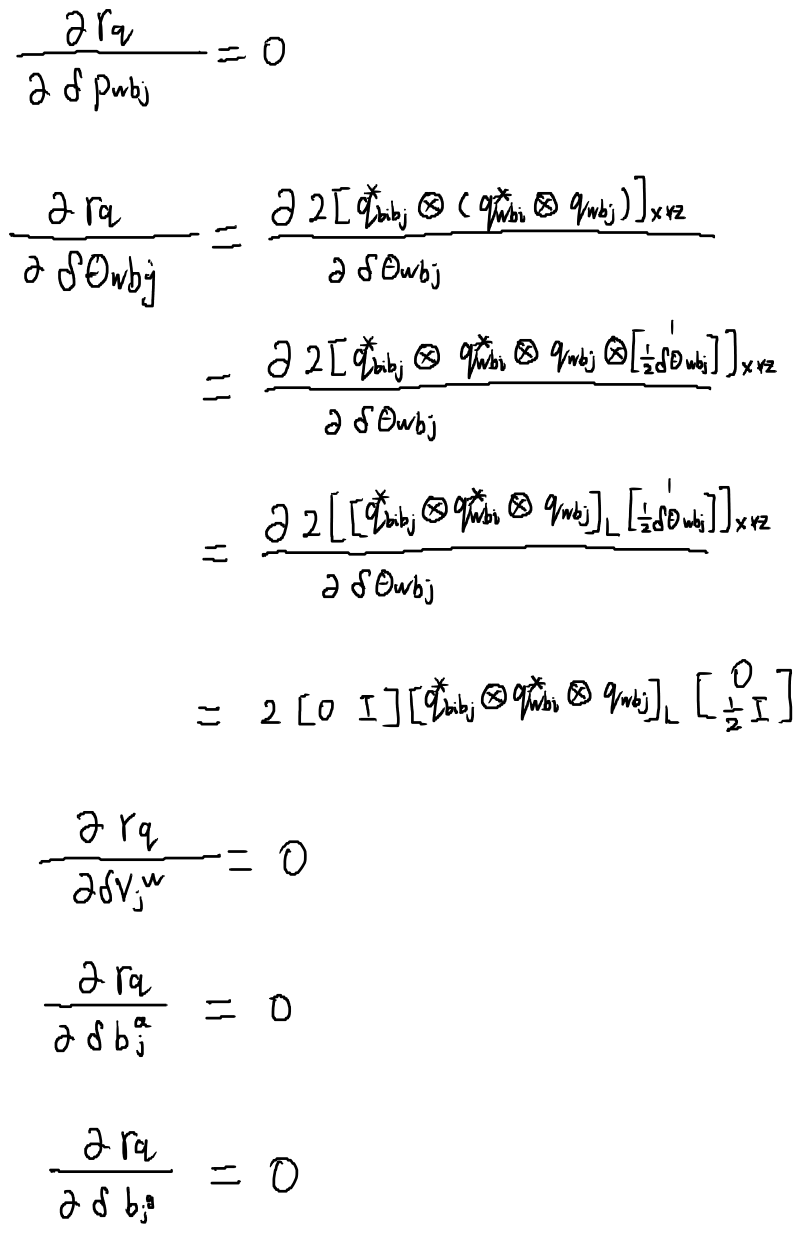
\(\mathbf{r}_{v}\)对状态量的雅可比
对状态i求雅可比

对状态j求雅可比

\(\mathbf{r}_{ba}\)对状态量的雅可比
对状态i求雅可比
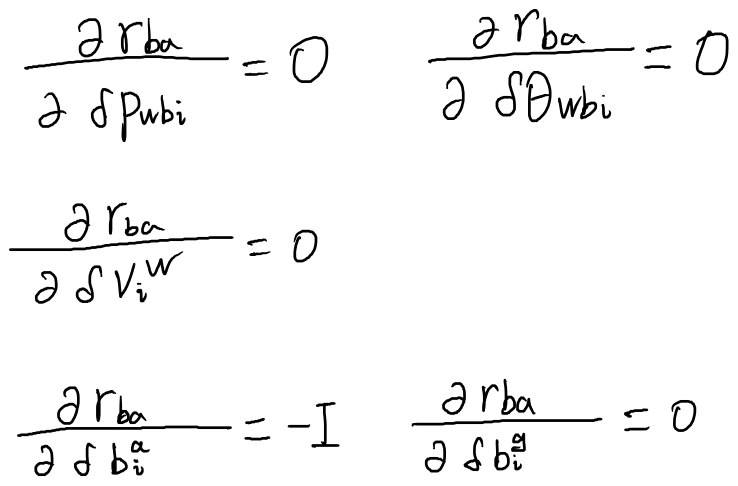
对状态j求雅可比
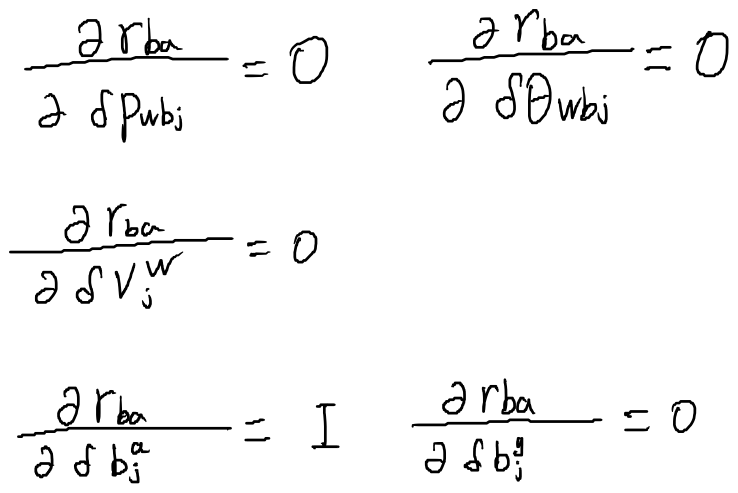
\(\mathbf{r}_{bg}\)对状态量的雅可比
对状态i求雅可比
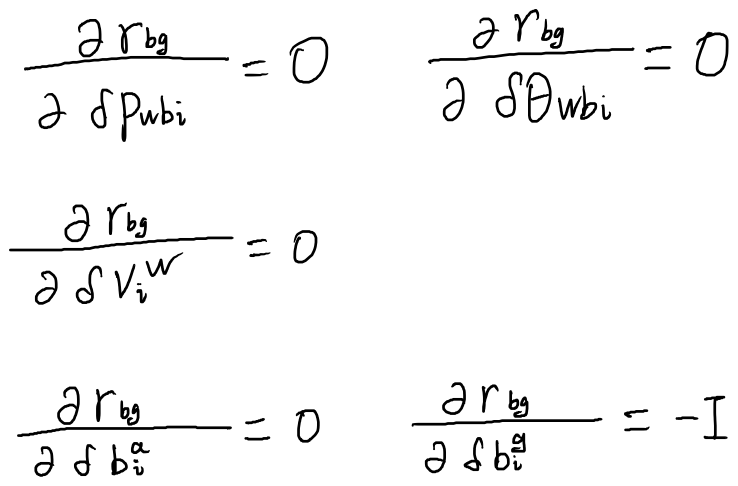
对状态j求雅可比
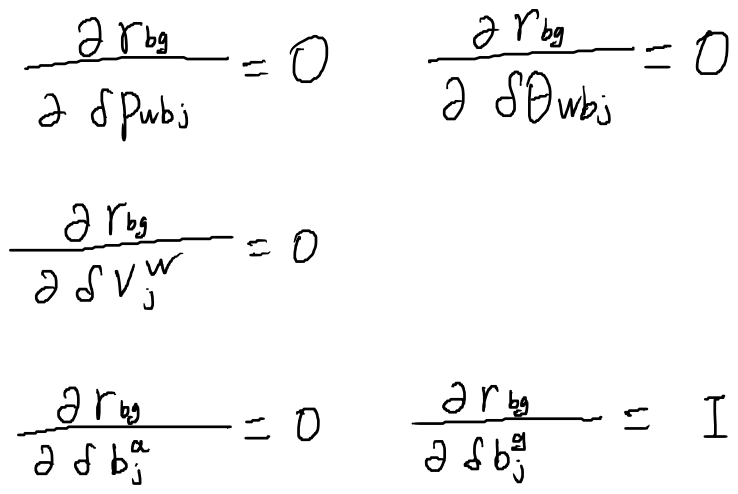
小结
残差

上面与vins-mono代码中 IntegrationBase::evaluate()对应
待优化变量
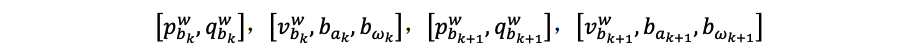
雅可比
计算 Jacobian 时,残差对应的求偏导对象为上面的优化变量,但是计算时采用扰动方式 计算,即扰动为:
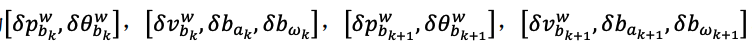
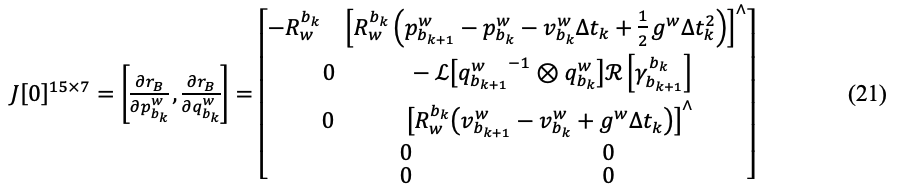
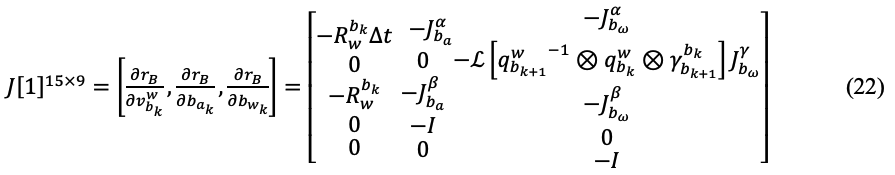


上面公式在vins-mono代码中对应:class IMUFactor : public ceres::SizedCostFunction<15, 7, 9, 7, 9> 对于 Evaluate 输入 double const const parameters, parameters[0], parameters[1], parameters[2], parameters[3]分别对应 4 个输入参数, 它们的长度依次是 7,9,7,9,分别对应 4 个优化变量的 参数块