LiDAR-Camera Calibration using 3D-3D Point correspondences

摘要
采用多个传感器来提供冗余信息,该信息可以减少具有错误测量的可能性。 在上述情况下,必须相对于单个参考帧从各种传感器获得数据,以便可以融合数据,并且可以利用冗余。
基于标记的[2]以及LIDAR和摄像机的自动校准已经提出,但在这些使用的方法和实验中讨论了高密度,更昂贵的激光雷达,并且当较低密度的LIDAR时,不太适用,例如 使用VLP-16。 我们提出了一种非常准确和可重复的方法来估计相机和激光器之间的6度自由度的外部校准参数
传感器及参数准备
我们提出的方法利用LIDAR和相机的传感器数据。 在启动激光雷达相机校准过程之前应该知道相机的内在参数.
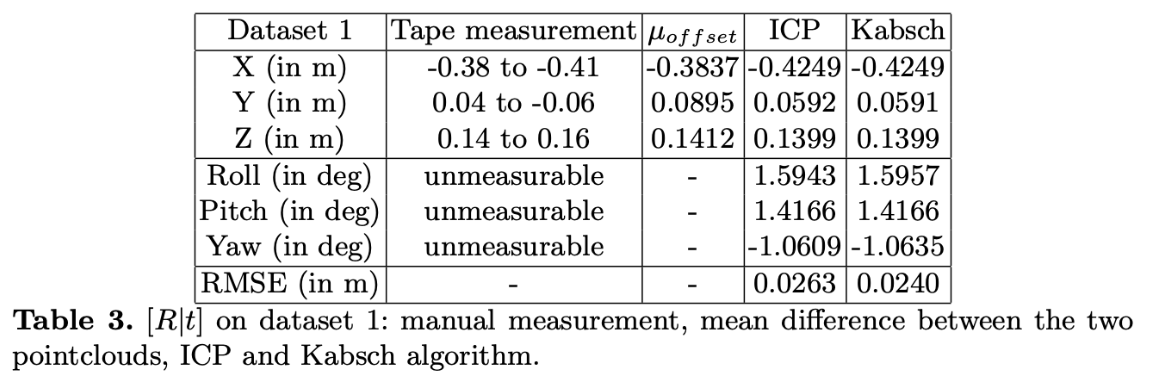
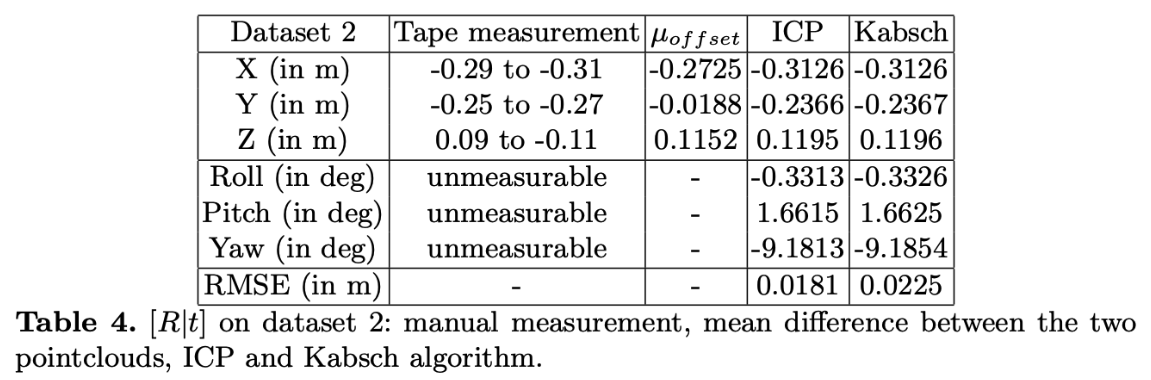
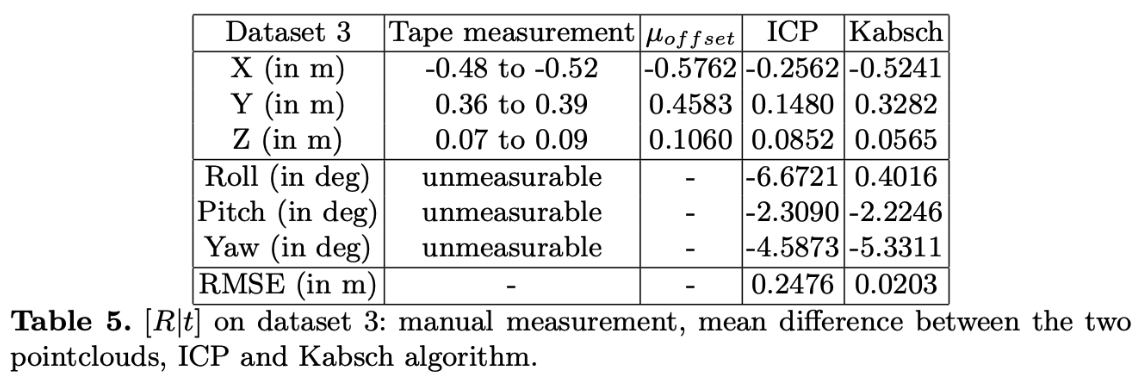
每次收集数据,LIDAR和相机都在3D空间中的任意距离保持,它们之间的转换是手动测量的。虽然,使用卷尺测量是粗糙的,但它用作使用各种算法获得的值的进行检查,测量平移量比旋转量容易的多,在其他情况下,当旋转极小时,我们假定它们为零。如果存在较大的角度,只能用三角板估计一下 。
2D-3D关联
在使用3D-3D点对应关系的方法之前,我们尝试了涉及2D-3D对应关系的方法。我们设计了自己的实验设置,以帮助校准激光器和相机。
实验设置
需要设置的标记:中空矩形纸板。
即使是普通纸板也可以很好地工作,因为我们将在即将到来的讨论中看到,提供更少的对应关系,而不是挖空的矩形纸板

数据提取
首先使用2D-3D方法:这种方法涉及通过匹配2D-3D点对应的方式在相机和激光器之间找到6-DOF变换,可以通过手动在图像中标记具有3-4像素的精度的图像中的特征点来容易地获得2D对应关系。
直接获取对应3d点的方法并不直接,这是因为lidar点云稀疏
平面纸板可以提供4个角点,在3D中,这些点可以通过直线拟合交点得到,在2D中,可以直接从marker的像素坐标获得。
如果空心纸板的外边框也使用,那么就可以提供8个3D-2D点关联,这样的设置允许有足够的数据来运行PNP算法的Ransac版本,并且还将有助于减少嘈杂的数据。
如果纸板的一侧与地面平行,由于激光水平扫描,那么可能只能获取到纸板的竖直边缘,而不能获取到水平边缘。为了克服这一点,我们将板倾斜以在一个边缘和地面平面之间制作大约45度来获取所有四个边缘获得点。 Ransac用于拟合LIDAR的点的直线。
这个节点允许手动绘制多边形,然后自动提取内部直线:
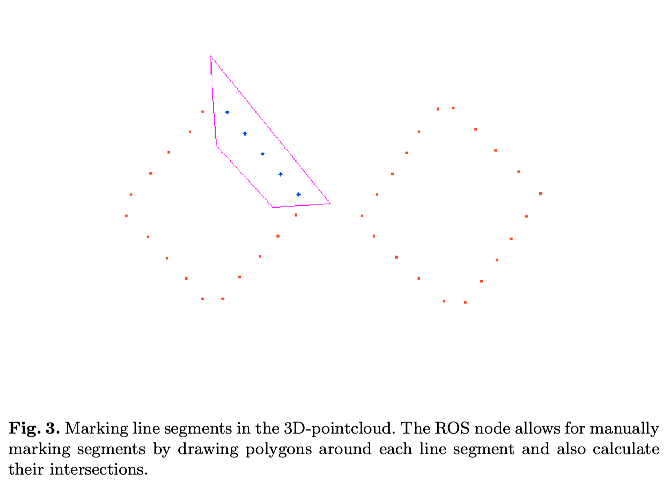
纸板上最突出的特征是角点,它可以在图像上相对容易地标记,并且由于我们对四个边缘具有相当准确的线条方程,因此它们的交叉点在3D中计算,这些空间中的直线实际上可能无法相交,但是非常接近。 我们将角点近似于两行之间最短线段的中点。
实验发现:两个线段之间的距离是\(10^{-4}\)米的距离,边缘长度之间的误差平均约为1厘米.
本实验获取到了20个角点:2个空心矩阵(2*8)+ 1个实心纸板(4)
问题求解
Perspective n-Point (PnP)方法用于寻找2D-3D匹配点对之间的刚体变换,其中式(1)展示了3D点投影方程:
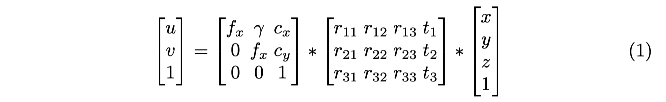
式(2)展示了使用的通用cost-function:

首先,使用了PNP和EPNP方法来最小化上述cost-func,然后通过手动剔除外点,进一步降低重投影误差到1.88个像素,但是,并没有求解出接近手动测量值的\(\{R,t\}\)
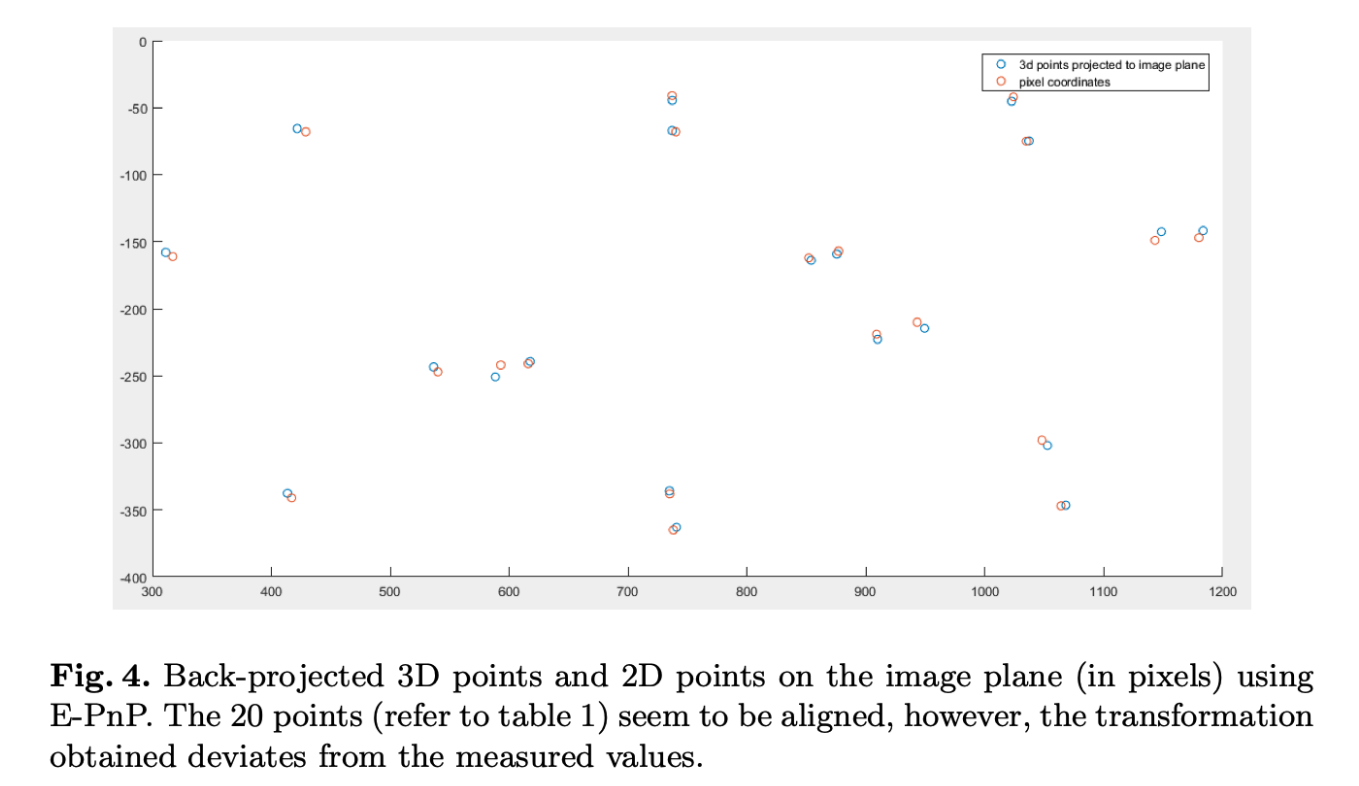
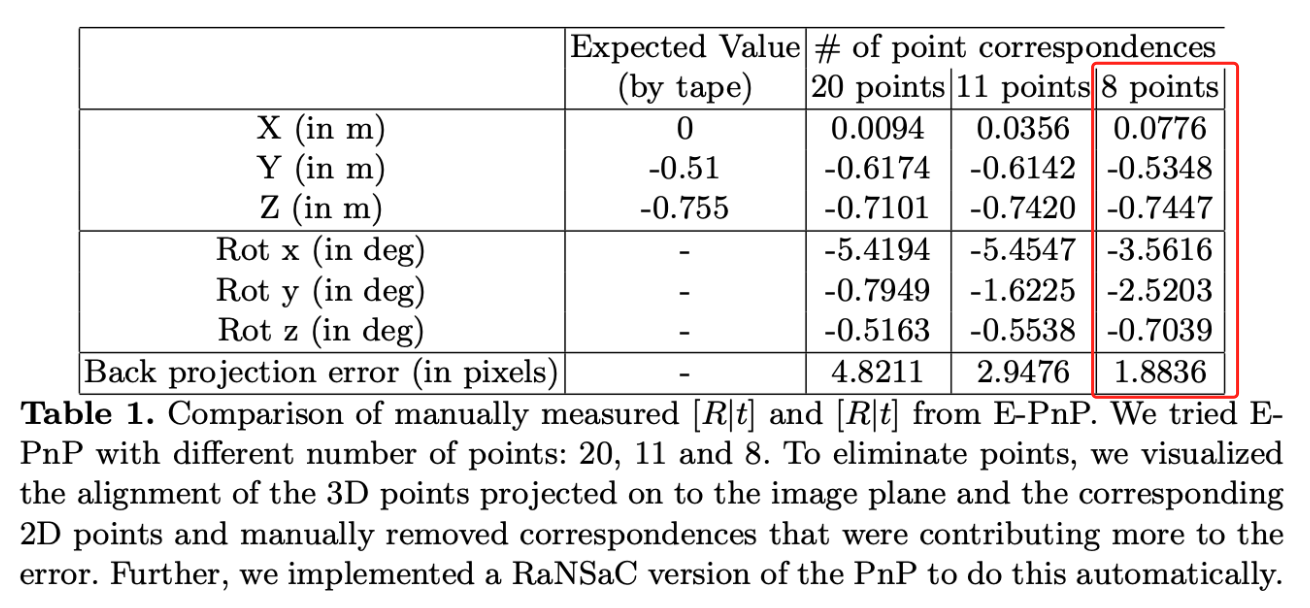
在上述实验中,由于激光雷达和相机比较接近,仅相差12厘米,且实验中仅使用了12个点进行EPNP,并没有达到预期效果。在随后的实验中,相机和lidar距离更远,减轻了误差的影响。
在检查数据时,我们发现了一些噪声点,这些噪声点造成了较大的重投影误差,我们运行了一个自定义的EPNP和RanSac算法,理论上可以确保滤除噪声点的影响。
通过实验发现,重投影误差小于1个像素,但是得到的\(\{R,t\}\)与期望值相差更大,这可能意味着最小化重投影误差可能不是一种整体最优的方法,因此必须使用其他更好的度量。
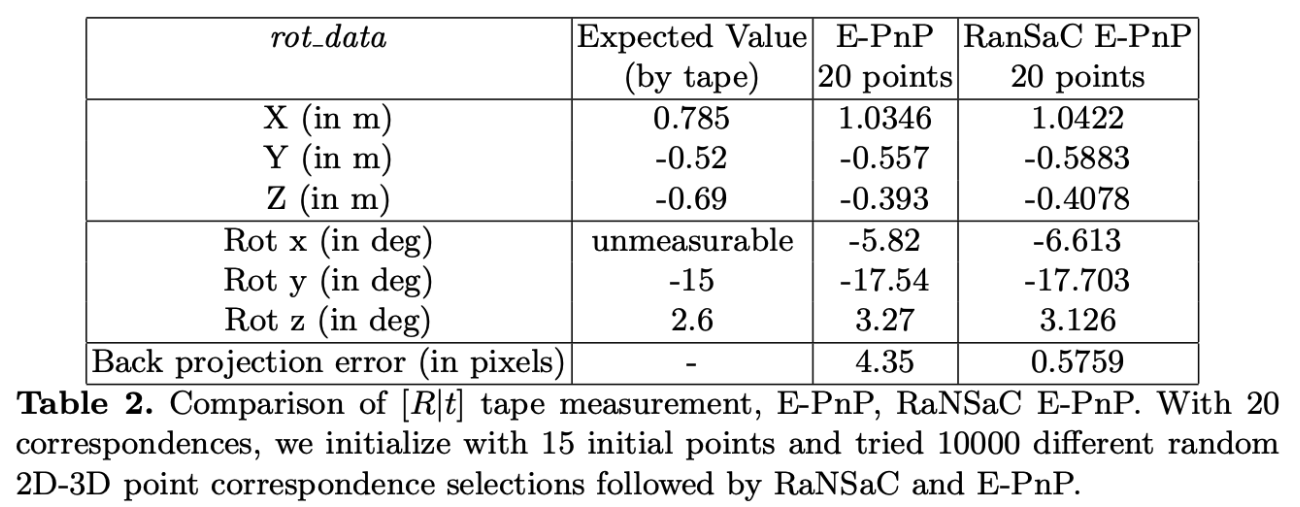
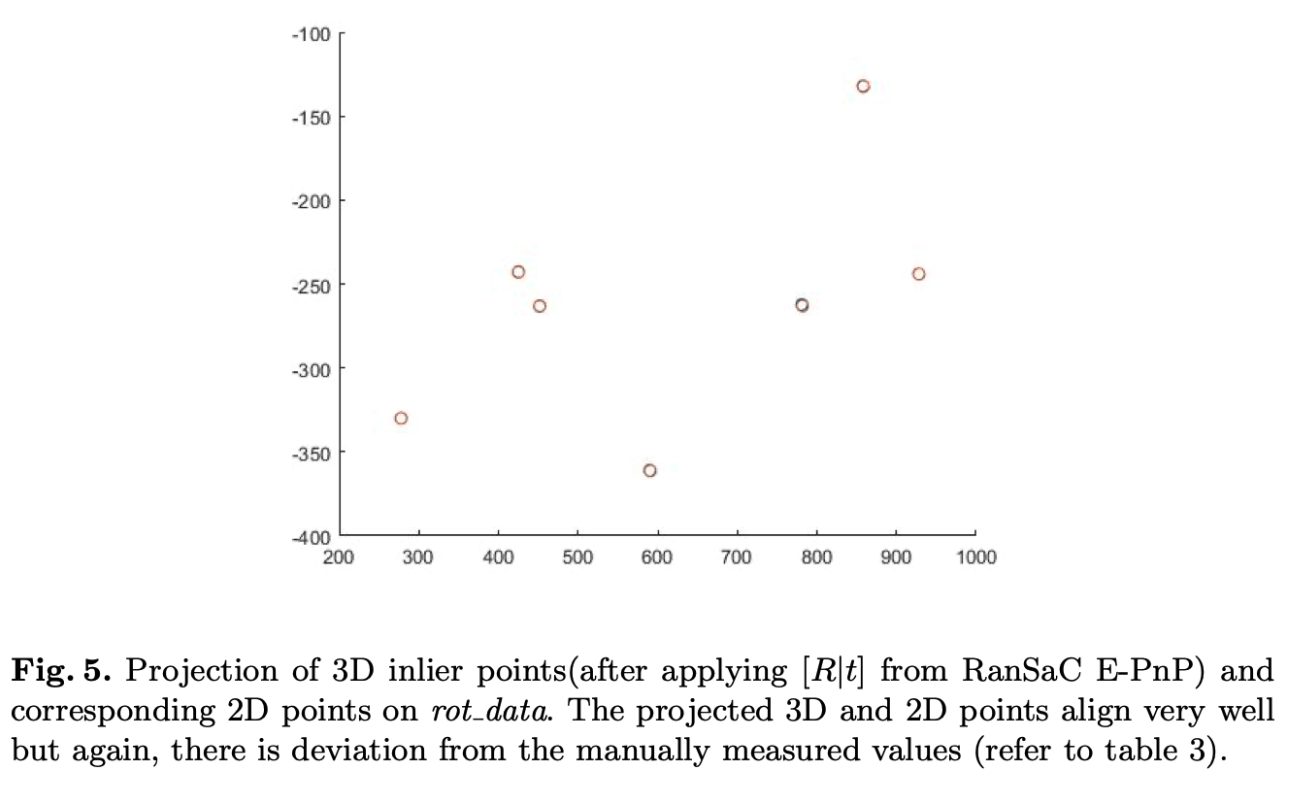
3D-3D关联
2D-3D对应方法在我们的实验设置中结果似乎不太理想,这可能是由于2D标记点的不准确或者使用含有噪声点进行PnP。尽管重投影误差似乎已经最小化,但是求出来的结果与测量值相差较大。
因此,这部分涉及使用增强 - 现实(AR)标签和LIDAR点云来找到外部校准参数,开源社区[7] [5]已释放多个版本的AR标签。 这里提出的方法使用ARUCO标签[5]。

为了找到相机与Velodyne之间的转换,我们需要两组3D点:一个在相机坐标系中,另一组在Velodyne坐标系中。 一旦发现这些点对应,就可以求解了。
实验设置
矩形纸板可以是任何任意尺寸。 我们执行的实验使用了一个Velodyne VLP-16 [3],其在单次扫描中仅具有16个环,与较高密度的LIDAR相比(每次扫描的32和64环)相比。 对于低密度的LIDAR,如果板的尺寸很小,并且LIDAR保持比特定距离更远,则击中板的环数变为低(2至3个环,导致边缘仅2至3点) ,使其非常困难地适应边缘(使用Ransac)
实验中使用的纸板的长度/宽度在45.0-55.0厘米之间,保持距离激光雷达2米左右距离,就可以有足够的点来拟合直线和计算交点。
相机坐标系中的3D点
ARUCO标记是特殊编码的模式,其促进标记本身的检测和纠错。 有关如何在这里找到工作的更多详细信息[5]
ArcoTag贴在纸板上,如果已知纸板的尺寸和ARUCO标记的位置,则可以容易地计算角落的位置(来自aruco标记的中心)。
ArcoTag提供相机坐标系和标记中心的\(\{R,t\}\)变换,这个变换可以用来将角点从标记所在的坐标系转换到相机坐标系。

激光雷达坐标系中的3D点
通过检测纸板的边缘可以找到激光雷达中的点,这又可以以类似的方式为拐角又可以解决第3节中描述的类似方式。
使用ArcoTag获取到的转换矩阵(特别是平移量)非常准确,一旦获取到两组3D点集合,就可以使用ICP算法进行求解了。
求解
ICP算法最小化式(3)表示的cost-func:
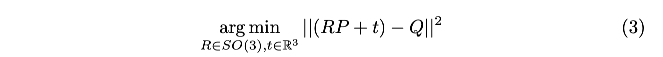
一般ICP算法认为点云中的最近点作为对应关系(有其他选择最接近点的其他变体,找到正确的对应关系可能是棘手的,可能导致不期望的解决方案.
由于在本方法中,点与点之间的对应关系是已知的,因此icp算法存在闭式解(Kabsch算法[9] [10]找到两点云之间的旋转,并且坐标系对齐后就可以找到平移):
下面的推导使用与[10]中的相同的参数。
首先,我们假设旋转是已知的,所以先求解平移量:
已知目标函数:
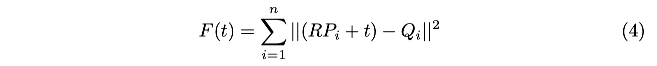
对平移量t求导并等于0:
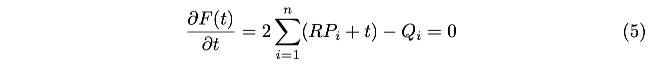
进一步有:

即:
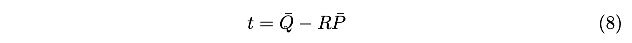
使用求出来的平移量替换式(4)中的部分,有:
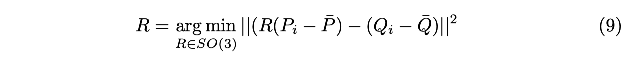
令:
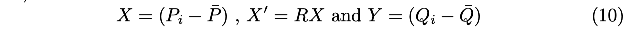
目标函数变成:
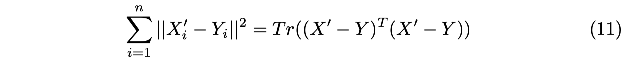
解释如下: 令\(X_{i}^{'}-Y_{i}=[x_i,y_i,z_i]^{T}\)
对不同的点得到的[x_i,y_i,z_i]进行堆叠,则有:
\[ \begin{aligned} (X'-Y)^{T}(X'-Y)&= \begin{bmatrix} x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end{bmatrix} \begin{bmatrix} x_1 & x_2 \\ y_1 & y_2 \\ z_1 & z_2 \\ \end{bmatrix} \\ &= \begin{bmatrix} x_1^{2}+y_1^{2}+z_1^{2} & m \\ n & x_2^{2}+y_2^{2}+z_2^{2} \end{bmatrix} \end{aligned} \]
实际上,我们的目标函数就是对角线元素之和。
进一步的,利用矩阵的迹的性质,可以进一步简化:
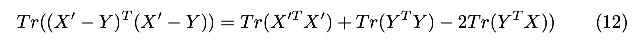
又因为旋转矩阵\(R\)是正交矩阵,因此有\(|X_i^{'}|^{2}=|X_i|^{2}\),进一步有:
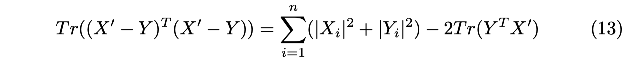
观察可知,前半部分是固定的,只有后半部分与旋转\(R\)有关,而且我们的目标是最小化,因此,即最大化后面的部分:
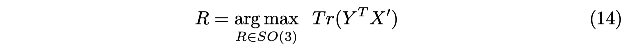
使用旋转\(R\)替换回\(X^{'}\),有:
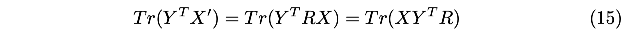
问题转化为,求\(R\)使得\(Tr(XY^{T}R)\)最大
进一步的,根据定理:

因此,对\(XY^{T}\)进行SVD分解,得到\(XY^{T}=UDV^{T}\),
令\(R=VU^T\),则
\[ Tr(XY^{T}R)=Tr(UDV^{T}VU^{T})=Tr((UD^{\frac{1}{2}})(UD^{\frac{1}{2}})^{T}) \]
因此,旋转\(R=VU^T\)
多帧求解
在初步实验中,观察到尽管在封闭空间中,激光雷达点云并非静止,为了减少噪声,采用多次扫描的方法。多帧数据中,保持激光雷达与相机空间关系不变:
对于每一帧数据估计出来的平移量,求均值有:
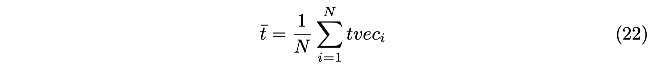
对于旋转量,先转换到四元数,然后求平均:
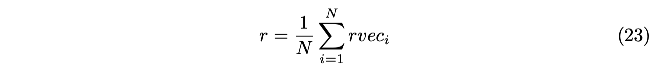
然后,还要进行归一化:
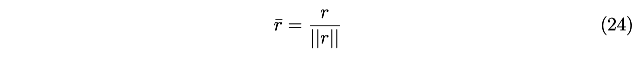
结果