Spatiotemporal Calibration of Camera and 3D Laser Scanner

摘要
我们提出了一种用于相机和3D激光扫描仪的开源时空校准框架。我们的解决方案基于常用的棋盘标记,需要在操作前进行一分钟校准,以提供准确和可重复的结果。该框架基于点对平面约束的批量优化,并且可以通过新颖的最小化来实现时间偏移校准,李代数中平面方程的连续表示以及B样条的使用。在仿真中评估了框架的属性,同时使用Velodyne VLP-16和SICK MRS6124 3D激光扫描仪通过两种不同的感官设置验证了性能。
介绍
提出的标定方法基于棋盘格的运动,以及一系列的来自相机和激光雷达的观测。然后执行批量优化来估计6dof刚体变换矩阵以及时间偏差。
该优化基于独立的激光雷达指向相机的平面约束,该平面约束由连续时间平面表示扩展,使得时间偏差可以得到优化。本文贡献在:
- 使用通用的棋盘格标记来估计lidar、camera的外参和时间偏移
- 新颖的李代数形式的连续时间最小化平面表示,使用B样条
- 对初值不敏感,可以收敛到预期结果
方法
提出的框架专用于刚体连接的具有全局快门相机和3D Lidar,并且假设相机内参已知且已经校正了。此外,假设传感器之间的时间偏移未知,且较小近似于常值。
标定过程需要包含标定板与传感器之间的相对运动,因此应该被激光雷达和相机连续观测得到。录制数据之后,按照下图的过程进行处理:

其中,对于相机,则使用opencv传统检测算法进行检测;对于激光雷达,首先将点投影成range-image,然后通过手动标记或半自动跟踪的方法来提取标定板对应的平面点。
如果不考虑时间偏移,标定可以描述为基于待求解位姿的点-面优化问题:
\[ T^{*} = \arg \min \sum_{i} \sum_{j} \pi(t_i)^{T}Tp_{i} \]
其中,
- \(T^{*}\)是期望得到的从激光雷达坐标系到相机坐标系的变换矩阵
- \(p_i\)表示标定板上第i个3D点的齐次坐标表示
- \(\pi(t_i)\)表示由相机在\((t_i+\Delta t)\)时刻估计得到的标定板平面等式。
提出的方法还注意到时间的校准,即考虑到点云中的每个点都对应一个时间戳,则目标函数变为:
\[ T^{*},\Delta t^{*} = \arg \min \sum_{i} \sum_{j} \pi(t_i+\Delta t)^{T}Tp_{i} \]
其中,
- \(\Delta t^{*}\)是待估计的时间差
- 要形成上式,需要知道每个3d激光点对应的时间戳以及对应任意时间的平面表示
- 本文使用LM以及g2o来求解
3D激光雷达时间偏移
对于机械旋转式激光雷达,都有一定的扫描周期,根据扫描起始和扫描结束,可以推断出对应点的时间:
vlp16
\[ t_{i}=t_{\text {cloud }}+\frac{\phi_{i}-\phi_{s}}{f\left(\phi_{e}-\phi_{s}\right)} \]
其中,
- \(t_{cloud}\)表示扫描起始时间
sick-mrs6124

连续时间平面表示
标定板在每一帧图像中都能检测到,由于相机内参、以及标定板物理参数已知,所以可以确定标定板坐标系到相机坐标系的变换。
因此,标定板的平面可以使用4维向量\((\bm{n},d)\)来表示,其中\(\bm{n}\)是平面法向量,\(d\)是到坐标系原点的距离。对于所有的图像,可以获取到离散时间下的一组平面方程集合。
为了确定各个时间戳的平面方程,需要对这些方程进行插值,因为4维的平面表示形式并非最小的表示方式,因此可能还需要做归一化处理。为了避免这个问题,提出一种使用类似于SO(3)以及对应的李代数so(3)的思想来表示平面法向量
该思想只需要使用两个参数就可以表示归一化法向量,因此,提出的方法几乎与[21]提出的球面插值法相同。
因此,平面的超参数化是因为法向量\(\bm{n}\),如果使用两个成分来表示,那么平面可以表示为:\((\bm{n},d) \rightarrow (\omega_x,\omega_y,d)_{3\times 1}\):
\[ \begin{aligned} \theta = acos(\bm{n}[2]) \\ \omega_{x}=-\bm{n}[1]*\frac{\theta}{\sin \theta} \\ \omega_{y}=\bm{n}[0]*\frac{\theta}{\sin \theta} \end{aligned} \]
这个思想来源于 [20]A. Bartoli, “On the non-linear optimization of projective motion using minimal parameters“ European Conference on Computer Vision (ECCV), Copenhagen, 2002, 340–354.
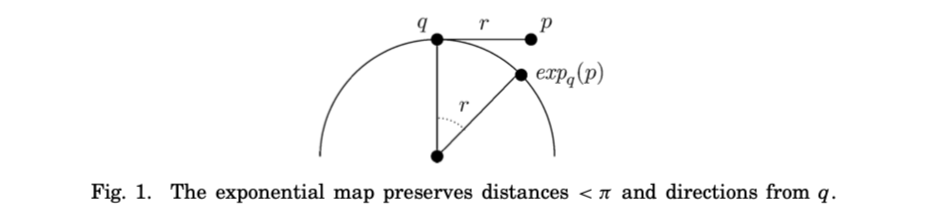
就是说,在3维欧氏空间中,以点(0,0,1)作为原点,以平行于x轴、y轴的方向作为坐标轴,展开一个超平面,那么3维欧氏空间中的矢量可以通过对数变换投影到该超平面上的一个点。
二维情况
三维情况
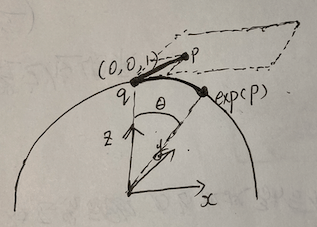
因此,选取3维欧氏空间中的单位向量\(q=[0,0,1]^{T}\),然后根据\(\cos \theta = q^{T} n\),那么可以得到\(\theta = \arccos (q^{T}n)=\arccos(\bm{n}[2])\),表示两个向量之间的夹角,特别的又因为球面半径是单位向量,因此,\(\theta\)也表示两个向量之间的球面距离。
特别的,根据下式可构成超平面上的点\(p=(\omega_x,\omega_y)\):
\[ \begin{aligned} \theta = \arccos(\bm{n}[2]) \\ \omega_{x}=-\bm{n}[1]*\frac{\theta}{\sin \theta} \\ \omega_{y}=\bm{n}[0]*\frac{\theta}{\sin \theta} \end{aligned} \]
其中,
\[ \begin{aligned} \sqrt{\omega_x^2 + \omega_y^2} &= \sqrt{ \frac{\arccos^{2} (n[2])}{\sin^{2}( \arccos(n[2])) } (n[0]^{2}+n[1]^{2}) } \\ &= \sqrt{ \frac{\arccos^{2} (n[2])}{1- \cos^{2}(\arccos(n[2])) } (1-n[2]^{2}) } \\ &= \arccos (n[2]) = \theta \end{aligned} \]
可以发现,在超平面上,点q和点p的距离等于球面上向量q和另一个向量之间的球面距离。
因此,实现了使用两个参数来表示欧氏空间中的向量,需要注意的是,\(\theta==0\)时,取\(\frac{\theta}{\sin \theta}=1\),特别的,仅适用于\(\theta < \pi\)的情况下。
平面方程插值
使用最小化的平面表示使得可以进行插值,然后返回到所需时间戳对应的4维的平面方程表示形式。
对于此任务,我们尝试了参数的线性插值,由于缺乏连续的微分导致优化陷入局部最小值。因此,提出了使用三次样条插值,确保最小平面表示具有一阶和二阶的连续微分。如下:
\[ \mathbf{s}(t)=\mathbf{s}_{0} B_{0}(t)+\sum_{i=1}^{n}\left(\mathbf{s}_{i}-\mathbf{s}_{i-1}\right) B_{i}(t) \]
其中,
- \(s(t)\)是在时间t插值得到的结果
- \(s_i\)是根据测量得到的第i个控制点的值
- \(B_i(t)\)是cumulative basis function的第i个成分
- \(n\)是B样条的阶数
对于李代数,则有插值方程如下:
\[ \mathbf{r}(t)=\log \left\{\exp \left(\mathbf{r}_{0} B_{0}(t)\right) \prod_{i=1}^{n} \exp \left(\boldsymbol{\Omega}_{i} B_{i}(t)\right)\right\} \]
其中,
- \(r(t)\)表示t时刻的李代数插值结果
- \(r_i\)表示李代数表示的第i个控制点
- \(\Omega_i=\log(\exp(r_{i-1})^{T}\exp(r_i))\)表示两个李代数之间的差值
来源于文献[23]:A. Patron-Perez, S. Lovegrove, and G. Sibley, “A spline-based trajec- tory representation for sensor fusion and rolling shutter cameras“, in International Journal of Computer Vision, vol. 113, no. 3, 208–219, 2015.
使用4阶B样条插值,cumulative basis function 如下:
\[ \mathbf{B}(u) = \frac{1}{6} \left[ \begin{array}{cccc} 6 & 0 & 0 & 0 \\ 5 & 3 & -3 & 1 \\ 1 & 3 & 3 & -2 \\ 0 & 0 & 0 & 1\end{array} \right] \left[\begin{array}{c} 1 \\ u \\ u^{2} \\ u^{3} \end{array} \right] \]
其中,
- \(u\)是从t2到t3之间的归一化时间(0~1),在实践中,我们还检查了检测到的棋盘的时间戳(T1,T2,T3,T4)是否均匀地分布在时间内,如果不满足这种情况,则不会执行插值
重要的是,可以使用[23]的已知方程来导出B样条曲线的jacobians,特别的,本系统使用了[24]所述的更有效的雅可比表示。
[24]C. Sommer, V. Usenko, D. Schubert, N. Demmel, and D. Cremers, “Efficient derivative computation for cumulative B-splines on Lie groups“, arXiv preprint, 1911.08860v1, 2019.
