3D激光雷达与全向相机外参标定

摘要
我们提出了一种使用全向摄像头系统对3D激光扫描仪进行外部校准的方法,该程序要求至少从3个视角同时从激光扫描仪和相机系统观察平面棋盘格图案,棋盘格的平面法向量和位于表面的3D点约束了激光扫描仪和全向相机系统的相对姿态,这些约束可用于形成外参标定的非线性优化问题,用于求解外参以及对应的协方差。
介绍
Scaramuzza et al. (2007).首先提出3d激光雷达与全向相机的外参标定问题,他们提出了使用手动选择关联点的方法完成标定。
本文提出的方法不需要手动选取对应点的3d激光雷达与全向相机的外参标定方法。
方法
在我们的校准程序中,我们使用安装在平面表面上的棋盘图案,我们将从现在开始将其称为目标平面,外部校准的近似设置以及用于实验的感知传感器(Velodyne HDL-64e 3D激光扫描仪和Pointgrey Ladybug3全向相机在图1中示出。
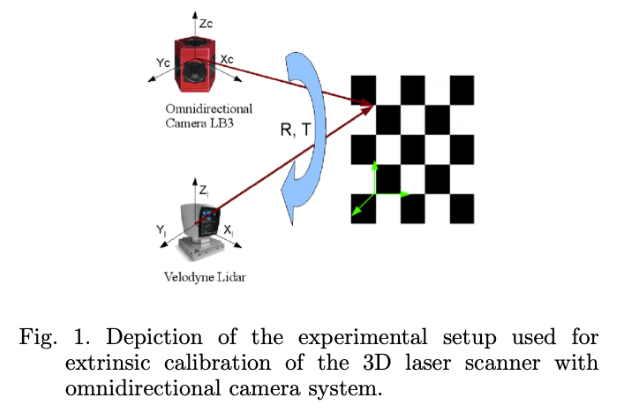
激光雷达内参标定
有关传感器的更多技术细节,参见McBride(2008)。 计算出的范围测量\(D_l\)由于TOF计算中的误差而包含一些偏差,因此具有来自实际测量的偏置校正\(\delta D\),因此制造商通常会为每条线束提供一个标定值\(\delta D\)来进行补偿,通常使用图2的方法:
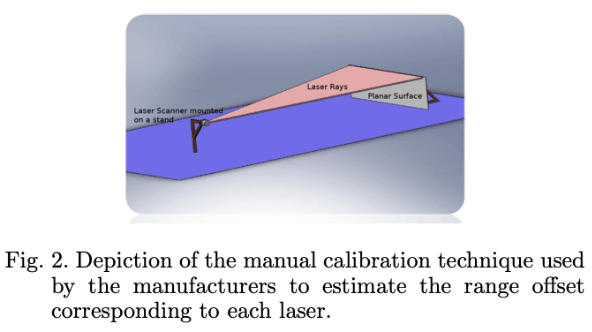
激光扫描仪安装在壁前的支撑件上,并且通过考虑墙壁和激光扫描仪之间的手动测量距离来计算范围测量中的偏移量:
\[ \delta D = D_m -D_l \]
- \(D_m\)是墙与雷达之间的距离手工测量值
- \(D_l\)是tof测量值
我们提出了一种鲁棒的方法来在范围测量中自动计算这种最佳偏移\(\delta D\)。
与制造商采用的校准方法相反,该方法仅要求用户将激光雷达放置于墙或者平面的前面,然后记录测量数据,如图3所示。

在墙壁或平面表面前方的传感器平台的不同位置记录激光测量。 现在,如果我们使用(1)中计算的\(\delta D\)校正,并考虑躺在墙壁上的点,它们应该都是共面的。
但是由于\(\delta D\)并非真值,因此这些点的重投影误差是显著的。因此可以通过最小化重投影误差来求解。
我们使用Ransac(Fischler和Bolles(1981))来估算在墙壁上的所有点的最佳拟合平面的等式,首先生成一个包含目标平面以及潜在激光点的边界框。然后,这些潜在激光点\(\{\tilde{Q}_l^i ; i=1,2,\cdots,N\}\)用于RANSAC进行平面拟合并返回内点。RANSAC步骤如下:
- 随机选取3个点from\(\{\tilde{Q}_l^i ; i=1,2,\cdots,N\}\)
- 求解3个点的平面方程
- 遍历其他点,寻找内点
- 重复,直到找到最佳平面方程
对RANSAC的最终结果进行参数化,\(\mathbf{N}=[n_x,n_y,n_z]^{\mathbf{T} }\),其中\(\|\mathbf{N}\|\)表示平面到坐标系原点的距离。
因此,平面中的点\(\tilde{P}=[X,Y,Z]^{T}\)在平面法向量\(\mathbf{N}\)的投影等价于平面距离\(\|\mathbf{N}\|\),即:
\[ \mathbf{P}\cdot\mathbf{N} = \|\mathbf{N}\|^{2} \]
记\(D\)为点的距离,\(\theta\)和\(\omega\)分别记为俯仰角和方位角,则有:
\[ \begin{aligned} X &=D \cos \theta \sin \omega, \\ Y &=D \cos \theta \cos \omega \\ Z &=D \sin \theta \end{aligned} \]
所以,使用平面法向量表示的点距离可以表示为(联合上面所有式子可得):
\[ D=\frac{\|\mathbf{N}\|}{n_{x} \cos \theta \sin \omega+n_{y} \cos \theta \cos \omega+n_{z} \sin \theta} \]
所以,我们现在获得了从RANSAC方法获得的点距离,以及激光雷达本身直接返回的点距离,可以构造如下非线性最小二乘:
\[ \delta D_{i}^{\prime}= \underset{\delta D_{i}^{\prime} }{\operatorname{argmin} } \sum_{i=1}^{64} \sum_{j=1}^{n} \left\|D_{i j}-\left(D_{l_{i j} }+\delta D_{i}^{\prime}\right)\right\| \]
- \(D_{i j}\)是根据
RANSAC计算的平面方程后得到的点距离 - \(D_{l_{i j} }\)是雷达直接返回的测距值
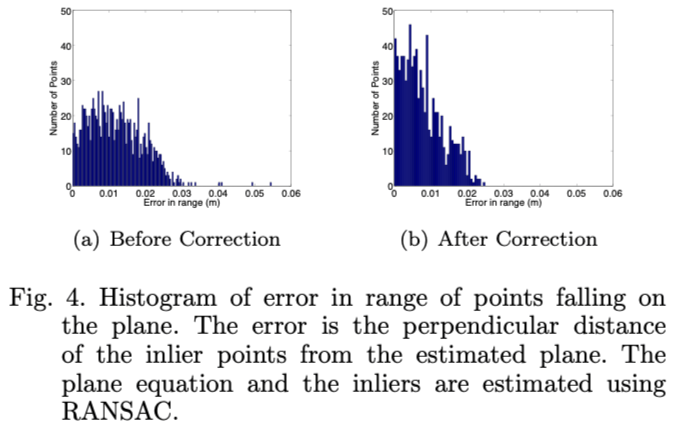
经过补偿之后的结果如图4所示:
全向相机
PointGrey Ladybug 3(LB3)是高分辨率全向摄像机系统,它有六个200万像素摄像头,其中五个CCD位于水平环中,另外一个位于垂直方向,使系统能够从超过80%的球形范围内收集视频。
摄像机由制造商预校准,因此单个相机的内在参数是已知的,同样的,以公共坐标系为参考基准(称为camera head),所有摄像头相对于参考坐标系的刚体变换也是已知的。
因此,我们需要估计camera head的姿势(相对于一些本地参考帧),以便我们可以代表相机头帧中的任何3D点,然后到任何相机的坐标系。
激光雷达与全向相机外参标定
外参标定方法与Zhang(2004)的方法相似,要求系统在不同的位姿观察平面pattern(如棋盘格),并根据激光雷达和相机同时观测的数据建立约束。
目标平面的法向量以及平面上的激光点之间存在关系,可用于约束相机和激光雷达的相对位姿关系。我们已知目标平面的方程,为了方便起见,以该平面构建坐标系,令
\[ Z=0 \]
令:
- \(\tilde{P}_{w}\)为在世界参考坐标系中的点(此处是attach到目标平面的坐标系)
- \({ }_{w}^{c_{i} } R\)是从世界坐标系\(w\)到第i帧相机坐标系\(c_i\)的旋转变换
- \({}^\mathrm{c_i}\mathrm{t}_{\mathrm{c}_{\mathrm{i} } \mathrm{w} }\)是平移量
因此,将一个世界参考坐标系中的点转换到第i帧相机参考坐标系可表示为:
\[ \tilde{P}_{c_{i} }={ }_{w}^{c_{i} } R \tilde{P}_{w}+{ }^{\mathbf{c}_{\mathbf{i} } } \mathbf{t}_{\mathbf{c}_{\mathbf{i} \mathbf{w} } } \]
其中,
- \(\tilde{P}_{c_{i} }\)是世界坐标系投影到第i帧相机坐标系的点
由于已知每个相机与camera head的相对位姿\({ }_{c_{i} }^{h} R,{ }^{\mathrm{h} } \mathbf{t}_{\mathbf{h c}_{\mathbf{i} } }\),因此可以将第i个相机坐标系中的点转换到camera head坐标系中:
\[ \tilde{P}_{h}= { }_{c_{i} }^{h} R \tilde{P}_{c_{i} }+{ }^{\mathbf{h} } \mathbf{t}_{\mathbf{h c}_{\mathbf{i} } } \]
因此,如果已知\({ }_{w}^{c_{i} } R\),\({}^\mathrm{c_i}\mathrm{t}_{\mathrm{c}_{\mathrm{i} } \mathrm{w} }\),就可以将世界坐标系中目标平面上的点\(\tilde{P}_w\)转换到camera head坐标系中。
论文采用了(Zhang (1998))的方法来获取相对目标平面(也就是棋盘格坐标系作为世界坐标系)的位姿变换。
特别的,对于pin-hole相机模型,3d点投影关系如下:
\[ \tilde{p} = K_i T_{w}^{ci} \tilde{P}_{w} \]
其中,
- \(K_i\)为3x4矩阵,是第i个相机的内参矩阵
- \(\tilde{P}_{w}\)为世界参考坐标系(棋盘格坐标系)下的点的齐次表达形式\(\tilde{P}_{w}=\left[\begin{array}{llll}X & Y & Z & 1\end{array}\right]^{\top}\)
- \(\tilde{p}\)为投影得到的图像点\(\tilde{p}=[u , v , 1]^{\top}\)
- \(T_{w}^{ci}\)为外参,是世界坐标系到相机坐标系的变换
假设图像点受独立同分布的噪声影响,外参\(T_{w}^{ci}\)的最大似然估计可以使用如下最小化重投影误差来表示:
\[ \underset{ { }_{w}{ }_{i} R,{ }^{\mathrm{c} } \mathbf{i} \mathbf{t}_{\mathbf{c}_{\mathbf{w} } \mathbf{w} } }{\operatorname{argmin} } \sum_{k=1}^{n} \sum_{j=1}^{m}\left\|p_{\hat{k} j}-K_{i}\left[{ }_{w}^{c_{i} } R{ }^{\mathbf{c}_{\mathbf{i} } } \mathbf{t}_{\mathbf{c}_{\mathbf{i} \mathbf{w} } }\right] \tilde{P}_{j}\right\| \]
其中,
- \(n\)表示n张图片
- \(m\)表示每张图片对应的m个点
- \({ }_{w}^{c_{i} } R=[\boldsymbol{r}_1,\boldsymbol{r}_2,\boldsymbol{r}_3]\)
- \({}^\mathrm{c_i}\mathrm{t}_{\mathrm{c}_{\mathrm{i} } \mathrm{w} }\)使用3维欧氏向量表示
因此,根据:
\[ \begin{aligned} Rp+t &= P_{new} \\ p &= R^{-1}(P_{new}-t) \end{aligned} \]
有:在第i个相机坐标系中的目标平面方程可以写成(利用平面\(Z=0\)的条件):
\[ \mathbf{r}_{3} \cdot\left(\mathbf{p}+{ }^{\mathbf{c}_{\mathbf{i} } } \mathbf{t}_{\mathbf{c}_{\mathbf{i} \mathbf{w} } }\right)=0 \]
其中,
- \(\boldsymbol{r}_3\)是旋转矩阵\({ }_{w}^{c_{i} } R\)第三列
- 旋转矩阵\({ }_{w}^{c_{i} } R\)第三列与点做
点乘相当于旋转矩阵的转置后的第3行与点做矩阵乘法,得到转换后的点的Z轴分量 - 同时,\(\boldsymbol{r}_3\)也是世界坐标系(棋盘格坐标系)的法向量方向
- \(\boldsymbol{p}\)是相机坐标系中,平面上的点
目标平面的法向量在第i个相机坐标系表示如下:
\[ \mathbf{N}_{\mathbf{c}_{\mathbf{i} } }=\left(\mathbf{r}_{\mathbf{3} } \cdot{ }^{\mathbf{c}_{\mathbf{i} } } \mathbf{t}_{\mathbf{c}_{\mathbf{i} \mathbf{w} } }\right) \mathbf{r}_{\mathbf{3} } \]
- 由于\(\boldsymbol{r}_3\)也是世界坐标系(棋盘格坐标系)的法向量方向,所以\(\|\mathbf{N}_{c_i}\|= \mathbf{r}_3 \cdot { }^{\mathbf{c}_{\mathbf{i} } } \mathbf{t}_{\mathbf{c}_{\mathbf{i} \mathbf{w} } }\) 表示第i个相机坐标系到目标平面的距离 (注意是点乘)
又因为第i个相机坐标系相对于camera head的位姿变换已知,因此可以计算以camera head坐标系为参考的目标平面法向量\(\mathbf{N}_h\):
(注意,这不是简单的向量做旋转,因为距离也会改变,即\(\| N_h\|\)是目标平面到camera head坐标系原点的距离),因此还要加上刚体变换的平移部分在法向量方向上的投影
\[ \mathbf{N}_{\mathbf{h} }= \frac{ { }^{h} R \mathbf{N}_{\mathbf{c}_{\mathbf{i} } } } {\left\|\mathbf{N}_{\mathbf{c}_{\mathbf{i} } }\right\|} \left(\left\|\mathbf{N}_{\mathbf{c}_{\mathbf{i} } }\right\|+\mathbf{N}_{\mathbf{c}_{\mathbf{i} } } \cdot \mathbf{h}_{\mathbf{t} \mathbf{h c}_{\mathbf{i} } }\right) \]
- 一旦我们已知了目标平面法向量在
camera head坐标系的表示,我们需要找到激光雷达坐标系中在目标平面中的3d点 - 我们使用上述
RANSAC方法来提取这些3d点 - 上述两种信息为外参标定提供了约束条件
令\(\{\tilde{P}_l^i ; i=1 , 2, \cdots ,n\}\)为提取的目标平面中的激光雷达点,利用待估计的外参,可以转换到camera head坐标系中:
\[ \tilde{P}_{h}^{i}={ }_{l}^{h} R \tilde{P}_{l}^{i}+{ }^{\mathbf{h} } \mathbf{t}_{\mathbf{h l} } \]
现在,如果将一束光线从camera head坐标系开始投射到目标平面上的一点,那么这个射线在平面法向量上的投影就等于从camera head坐标系到目标平面的距离,因此,从m个不同的视角获取数据,可以构造如下目标函数:
\[ F= \sum_{i=1}^{m} \sum_{j=1}^{n}\left(\frac{\mathbf{N}_{\mathbf{h} }^{\mathbf{i} } }{\left\|\mathbf{N}_{\mathbf{h} }^{\mathrm{i} }\right\|} \cdot\left({ }_{l}^{h} R \mathbf{P}_{l}^{j}+{ }^{\mathbf{h} } \mathbf{t}_{\mathbf{h l} }\right)-\left\|\mathbf{N}_{\mathbf{h} }^{\mathbf{i} }\right\|\right)^{2} \]
其中,
- \(\mathbf{N}_{\mathbf{h} }^{\mathbf{i} }\)是目标平面在
camera head坐标系中的第i个位姿对应的法向量 - 第一项表示激光雷达点在
camera head坐标系构成的向量,在法向量方向的投影 - 第二项表示由相机信息获取的
camera head坐标系与目标平面的距离
外参标定需要的最少视角个数
需要至少三个目标平面的非共面观点来完全限制优化问题(17)以估计校准参数,

只有一个平面的情况:如图5(a)所示:
- 当保持姿态不变,沿目标平面萍乡的方向进行平移时,目标函数的值不变
- 以平面法向量为轴进行旋转时,目标函数的值也不变
相似的,对于只有两个视角的情况:如图5(b)所示:
- 传感器沿着平面交叉线平移并不改变目标函数值,从而在该方向上产生大的不确定性
估计参数的协方差
通过最小化目标函数得到的参数估计会由于传感器测量的不确定性导致具有一定的误差,如激光雷达测距误差约为0.02m。知道这种不确定性是非常重要的,以便在任何视觉或SLAM算法中使用此处计算的参数。
Haralick(1998)已经描述了通过任何标量非线性优化函数传播测量协方差的方法,唯一的假设是标量函数是非负的,具有有限的第一和二阶偏微分,对于理想数据即其值为零,并且输入中的随机扰动足够小,以便可以近似输出一阶泰勒系列扩张。
前文提出的目标函数满足这些假设,因此可以用这个方法来估计参数的协方差。
假设camera head坐标系相对于激光雷达坐标系可以用参数来表示:
\[ \Theta=\left[{ }^{1} \mathbf{t}_{\mathbf{l h} }, \mathbf{\Phi}_{\mathbf{l h} }\right]^{\top} \]
其中,
- \({ }^{1} \mathbf{t}_{\mathbf{l h} }=\left[t_{x}, t_{y}, t_{z}\right]^{\top}\)表示从h坐标系到l坐标系的平移变换(在l坐标系的表示)
- \(\boldsymbol{\Phi}_{\mathrm{lh} }=\left[\theta_{x}, \theta_{y}, \theta_{z}\right]^{\top}\)表示从h坐标系到l坐标系旋转
关于参数\(\Theta\)的协方差如下:
\[ \Sigma_{\Theta}=\left[\frac{\partial^{2} F}{\partial \Theta^{2} }(X, \Theta)\right]^{-1} \frac{\partial^{2} F^{T} }{\partial X \partial \Theta}(X, \Theta) \Sigma_{X} \frac{\partial^{2} F}{\partial X \partial \Theta}(X, \Theta)\left[\frac{\partial^{2} F}{\partial \Theta^{2} }(X, \Theta)\right]^{-1} \]
其中,
- \(X=\left[\mathbf{N}_{\mathbf{h} }^{\mathbf{1} }, \tilde{P}_{l}^{1}, \tilde{P}_{l}^{2} \ldots \mathbf{N}_{\mathbf{h} }^{\mathbf{i} }, \tilde{P}_{l}^{1}, \ldots\right]^{T}\)表示观测信息(包括平面法向量和目标平面中的激光点)
实验
仿真实验(略)
真实环境实验
所提出的外在校准方法已经在由安装有3D激光传感器和全向相机系统的车辆收集的实际数据上进行了测试,如图8所示。

我们有两套结果验证算法的准确性,在第一种情况下,我们考虑了类似于校准设置的设置:在车库内进行校准,棋盘图案安装在所有可用的平面表面上(包括侧壁和底层),如图9所示,由不同颜色表示的来自不同平面的点已经投影到相应的图像上。

在第二种情况下,我们将车辆从车库外面带走,并从福特校园周围的行驶中的车辆中收集了一些数据,在全向相机系统的5个摄像机上的5个摄像机上的360度视场的投影的结果如图10所示。

代码库
https://github.com/SubMishMar/cam_lidar_calib