T-LOAM: Truncated Least Squares LiDAR-Only Odometry and Mapping in Real Time

摘要
提出了一个基于截断最小二乘法的新颖的、计算效率高、鲁棒的纯激光里程计。我们的方法侧重于减轻异常值的影响,允许在退化发生的稀疏,嘈杂或杂乱的情况下允许强大的导航。
作为预处理,使用了多区域的地面提取,动态曲率体素的聚类方法来完成3D点云的分割和滤除不稳定目标的工作。
提出一个新颖的特征提取模块,用于区分:边缘特征、球形特征、平面特征、地面特征。
作为前端,是一个基于分层特征的纯激光雷达里程计,通过截断最小二乘法来直接处理不同的特征以进行精确地运动估计。预处理模型和运动估计精度已经在 KITTI 里程计基准以及各种校园场景中进行了评估。 实验结果证明了所提出的T-LOAM的实时能力和优越的精度优于其他最先进的算法。
变量约定
DCVC聚类: Dynamic curved-voxel clusteringMRGE地面提取:Dultiregion ground extractionTLS截断最小二乘:Truncated least squares\(t_k\): 第k帧激光扫描结束的时间
\(L_k\): 时间\(t_k\)对应的LiDAR body坐标系
\(Q_i,S_j\):
MRGE的第i个象限,第j部分\(\mathbb{F}_{k}^{v}, \mathbb{F}_{k}^{b}\): 时间\(t_k\)
MRGE的前景和背景\(\mathbb{F}_{k}^{d}\): 在时间\(t_k\)由\(\mathbb{F}_{k}^{v}\)输出的
DCVC模型\(\mathbb{F}_{k}\): 在时间\(t_k\)对应\(L_k\)坐标系的所有特征
\(F_{k}^{e}, F_{k}^{s}, F_{k}^{p}, F_{k}^{g}\):边缘、球形、平面、地面特征
\(\mathbb{M} \mathbb{l}_{k}^{w}\):时间\(t_k\)的世界坐标系中的子图第k特征点
\(x_{k}^{w}\):时间\(t_k\)对应的机器人在全局坐标系的状态
介绍
在本文中,已经实施了一系列改进,以解决当前激光SLAM框架中存在的缺陷。 截断最小二乘(TLS)方法创新的应用于扫描匹配,使T-LOAM对于异常值更加鲁棒,并减轻其对初始值解决方案的依赖性。 原始点云通过精心设计的预处理模块进行了分割,以提取四个独特的功能:边缘特征,球形特征,平面特征和地面地面。 为了实现更加平滑的里程计,通过TLS方法构建了与不同特征相关的三种残差函数。 最后,构建如图1所示全局一致的地图。
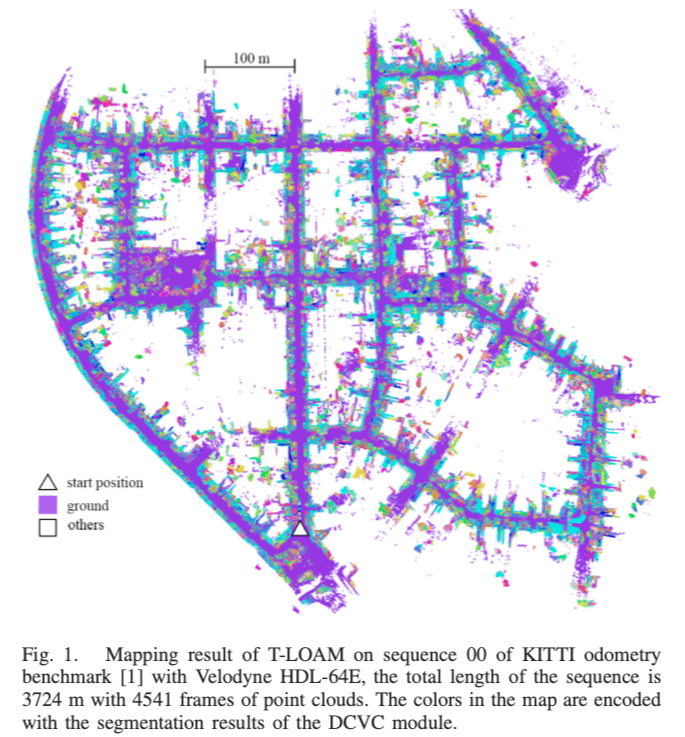
使用了KITTI Odomerty数据集来与其他state-of-art的方法相比,如F-LOAM,A-LOAM,SuMa等,实验结果表明T-LOAM在大多数序列实验场景中达到更优越的性能。
本文主要贡献:
- 提出一个基于截断最小二乘TLS的高效率鲁棒激光里程计,用于进行导航和构建全局一致性高的点云地图。
- 利用MRGE地面提取和DCVC聚类来实现一系列预处理步骤,提高点云分割的精度
- 首次使用
Open3D进行激光SLAM框架的开发,并开源
本方法受graduated nonconvexity(GNC)方法的启发,这在计算机视觉字段中执行了各种匹配和优化任务,已经证明有效。根据Convex优化理论基于TLS构建一种新颖的姿态优化函数,以估算6自由度的变换。
该实现遵循如图2所示,并通过多线程和OpenMP [28]设置并行化以保证算法的整体运行效率,另外还使用了ROS社区的nodelet功能包来实现Zero copy.
数据集与系统硬件介绍
本文中使用的TX2机器人是远程化的车辆,这是由双无刷电机驱动,由670-WH电池供电。LIDAR的安装高度设置为0.75米,以保证全向扫描。 通过遥控记录实验数据集。 此外,LIDAR采样频率设定为10 Hz。
采用两台计算机评估所提出的框架的实时能力,包括NVIDIA Jetson TX2(ARM Cortex-A57 CPU)以及2.5-GHz i7-10750H CPU的笔记本电脑。
所有模块由C ++实现,并将Nodelet包作为Ubuntu 18.04 Linux中的唯一节点集成到ROS [29]中,以完成它们之间的零拷贝传输。 本文中提出的实验仅利用这些系统中的CPU运行。
预处理模块
框架总览
T-LOAM框架如图2所示
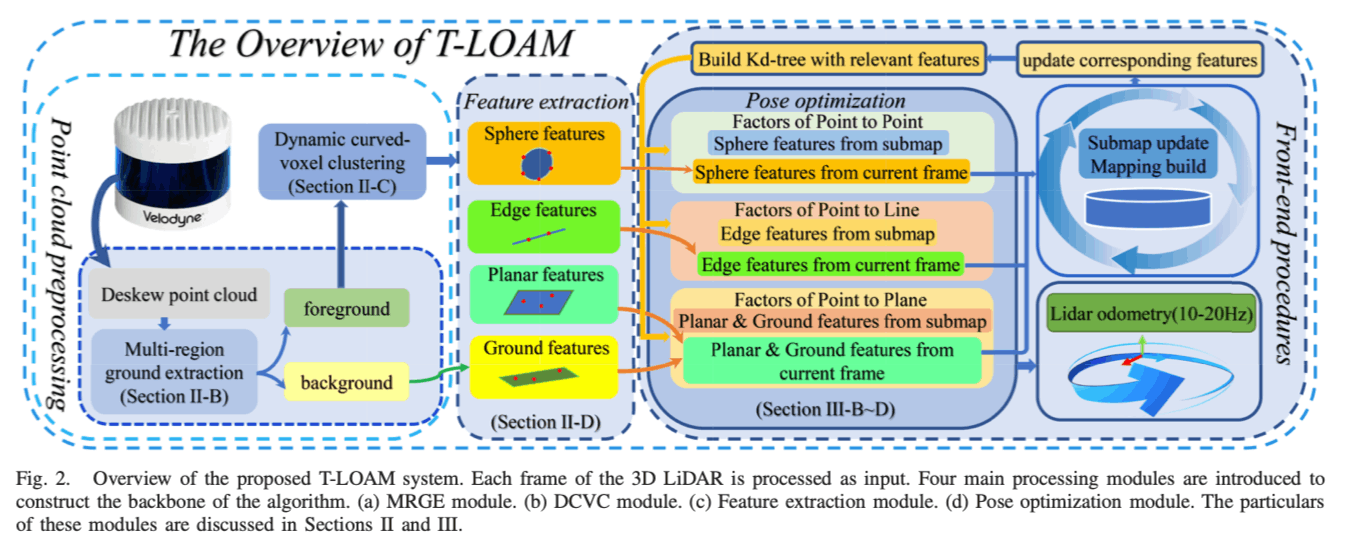
首先,对激光扫描进行关于旋转的畸变矫正,然后,将点云输入到MRGE模块中以获取前景\(\mathbb{F}_{k}^{v}\)和背景\(\mathbb{F}_{k}^{b}\)。随后,使用DCVC方法来对前景进行分割,并滤除不稳定的类别,得到\(\mathbb{F}_{k}^{d}\)。
此外,通过特征提取模块来分别得到特征点\(\mathbb{F}_{k}=\left\{F_{k}^{e}, F_{k}^{s}, F_{k}^{p}, F_{k}^{g}\right\}\),通过预处理扫描,关联的特征点通过位姿优化模块配准到子图上,得到全局一致性地图。此外,基于连续的激光扫描位姿优化得到的平移,将用于对当前帧扫描特征点云进行平移量的矫正。
多区域地面提取
地面点云通常占据了车载激光雷达扫描的大部分,并通常具有较简单的数学模型,有利于处理。
特别的,这些特征可以直接用于构造位姿优化的约束。但是,仅使用单个平面模型不足以准确表示复杂地形中的分布,因此,采用了MRGE方法来提高分割精度。

在算法一中,原始的激光扫描首先根据极坐标分为多个象限(默认是4),如图4(a)所示。其次,对于每一个象限,都将继续分为多个子区域(默认为3),如图4(b)所示,其中,每个子区域的边界如下计算:
\[ \theta_{i}=\theta_{s}+\frac{n}{b} \alpha \cdot k_{i} \]
\[ \lambda_{i}=\left\{\begin{array}{ll} h\left(\frac{1}{\tan \left(\theta_{i}\right)}\right), & \text { if } i \geq 1 \\ 0, & \text { if } i=0 \end{array}\right. \]
其中,\(\theta_s\)是激光扫描的起始仰角,\(b\)是子区域数,\(n\)是可能包含地面点的激光线束数总和。特别的,\(\alpha\)代表激光雷达的垂直角分辨率,\(h\)表示激光雷达的安装高度,\(k,i\)分别表示区域的系数和索引。
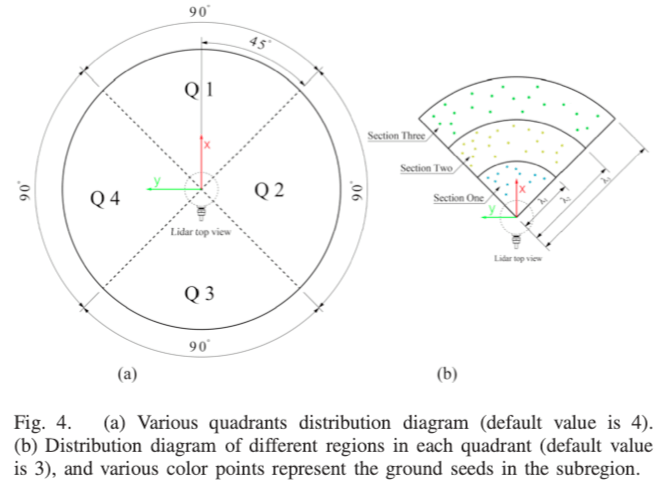
对于自动驾驶车辆来说,地面点的高度坐标分量通常位于最低位置,因此,可以利用这个先验信息来根据高度值对区域点云进行整理。
种子点在指定的阈值\(\tau\)内进行选择,主要用于拟合初始的平面模型。为了提高模型精度,多轴线性回归方法量身定制以计算相关参数,主要方向被加权,以减轻异常值的影响。线性平面模型被量身定制以反映子区域的分布,通过如下:
\[ \begin{aligned} a x+b y+c z+d &=0 \\ n^{T} \mathrm{p} &=-d \end{aligned} \]
其中,
- \(n=\left[\begin{array}{lll}a & b & c\end{array}\right]^{T}\),表示平面法向量
- \(\mathrm{p}=\left[\begin{array}{lll}x & y & z\end{array}\right]^{T}\),表示平面上的点
特别的,协方差矩阵M用于获取对应的每个子区域中指定的种子点的分散性:
\[ \mathcal{M}=\sum_{i=1}^{|s|}\left(s_{i}-\bar{s}\right)\left(s_{i}-\bar{s}\right)^{T}=\left(\begin{array}{lll} a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \\ c_{1} & c_{2} & c_{3} \end{array}\right) \]
其中,\(\bar{s} \in \mathbb{R}^{3}\)记为子区域中的所有点\(s_{i} \in S\)的均值。
下一步,计算出三个主方向:
\[ \begin{array}{l} v_{x}=\left[\begin{array}{l} b_{2} c_{3}-b_{3} b_{3} \\ a_{3} b_{3}-a_{2} c_{3} \\ a_{2} b_{3}-a_{3} b_{2} \end{array}\right], \quad v_{y}=\left[\begin{array}{l} a_{3} b_{3}-a_{2} c_{3} \\ a_{1} c_{3}-a_{3} a_{3} \\ a_{2} a_{3}-a_{1} b_{3} \end{array}\right] \\ v_{z}=\left[\begin{array}{l} a_{2} b_{3}-a_{3} b_{2} \\ a_{2} a_{3}-a_{1} b_{3} \\ a_{1} b_{2}-a_{2} a_{2} \end{array}\right] \end{array} \]
为了减轻异常值对法向量估计的影响,每个主方向加权,并应用线性回归来细化正常向量。 权重值是所示的每个主方向的二范数,如下:
\[ \begin{aligned} n &=\sum_{k \in\{x, y, z\}} w_{k} v_{k} \\ w_{x} &=v_{x}[0]^{2}, \quad w_{y}=v_{y}[1]^{2}, w_{z}=v_{z}[2]^{2} \end{aligned} \]
其中,\([]\)操作符表示取该向量对应的元素
参数\(d\)可以根据平面方程和\(p,\bar{s}\)计算获得,即当法向量\(n\)获取后,将一个点代入最终的平面模型即可计算得到。
动态曲率体素聚类
为了准确高效对点云进行分割,提出了DCVC方法。改进的空间体素类型满足[24]中描述的三个重要方面,以及与点云的空间分布更加对应。
- 定义1: 第i,j,k个动态弯曲的voxel表示一个3D空间的体素单元,其根据配置可以如下计算:
\[ \begin{aligned} D C V_{i, j, k}=\left\{P(\rho, \theta, \phi)=\mid \rho_{i}\right.& \leq \rho<\rho_{i}+\Delta \rho_{i} \\ \theta_{j} & \leq \theta<\theta_{j}+\Delta \theta_{j} \\ \phi_{k} &\left.\leq \phi<\phi_{k}+\Delta \phi_{k}\right\} \end{aligned} \]
其中,每个\(P(\rho, \theta, \phi)\)是极坐标系中的极径\(\rho\)、方位角(俯仰)\(\theta\),极角(水平)\(\phi\)。特别的,\(\Delta \rho_i,\Delta \theta_j, \Delta \phi_k\)表示根据点云的稀疏性和距离值调整的每个体素单元的边界上下界之差(即体素的尺寸)。
另外,每个方向上的体素的增量可以计算如下:
\[ \begin{array}{l} \Delta \rho_{i}=\rho_{s}-\left(a \times s_{i}+b\right) \times \Delta \rho \\ \Delta \theta_{j}=s_{j} \times \Delta \theta \\ \Delta \phi_{k}=s_{k} \times \Delta \phi \end{array} \]
其中,
- \(\rho_s\)表示起始的体素极径
- \(s\)表示步长
- \(\Delta \rho,\Delta \theta, \Delta \phi\)分别对应极径、方位角、极角的增量
- \(a,b\)是体素系数,其可以根据各种光束的点云和3D LIDAR的密度来确定
为了更好地理解实际分布,在图5中可视化两个相邻的空间动态体素。
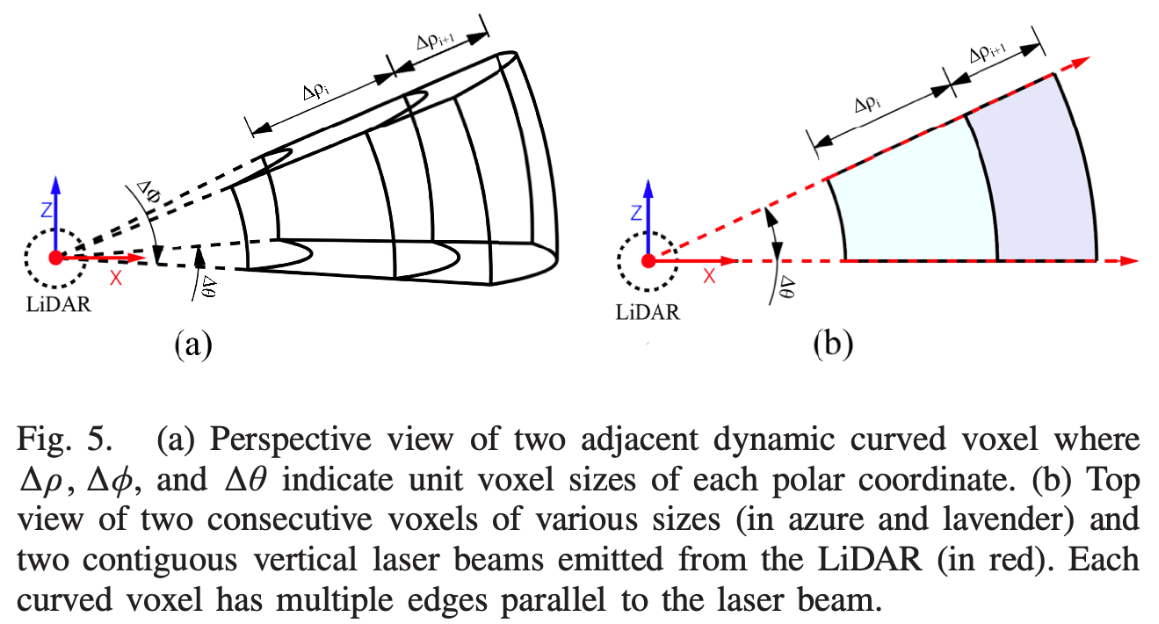
这个图右图有点问题,图中的z轴应该是y轴才对,因为右图是俯视图
稀疏系数可用于调节极径方向上不同距离的体积,这有利于防止对空间中相邻物体区分失败。
DCVC方法总结成算法2。

我们首先将笛卡尔坐标系的点云转换到极坐标系中,同时建立弯曲的体素。
然后,将非空的动态体素构建成哈希表,以提高搜索效率。
随后,根据哈希表映射关系,搜索当前点所在体素的周围体素,并将它们合并到统一标签中。
最后,我们返回每个点的类别信息,并提供合成判断,以滤除一组或潜在的动态目标,以获得最终的点云\(\mathbb{F}_{k}^{d}\)。以这种方式,当各种对象彼此依然相邻时,显著抑制了不正确的分割分类的发生。
特征提取
很明显,LOAM[10]中呈现的算法容易受几何退化场景的影响,这将直接衰减激光雷达测量仪的精度甚至使其失败。
为了提高纯激光雷达里程计的稳定性,T-LOAM将从\(\mathbb{F}_{k}^{d}\)和\(\mathbb{F}_{k}^{b}\)提取4个可区分的几何特征,包括边缘特征\(F_{k}^{e}\),球面特征\(F_{k}^{s}\),平面特征\(F_{k}^{p}\)和地面特征\(F_{k}^{g}\)。
背景\(\mathbb{F}_{k}^{b}\)首先进行降采样,边缘则使用LOAM[10]方法,根据平滑度提取:
\[ c=\frac{1}{|s| \cdot\left\|p_{i}\right\|}\left\|\sum_{m \in s, m \neq i}\left(p_{m}-p_{i}\right)\right\| \]
其中,\(s\)表示同一激光束的连续10个点的集合,即包含点\(p_i\)左右两侧的5个点
另外,球面特征\(F_{k}^{s}\)和平面特征\(F_{k}^{p}\)的垂直部分可以通过PCA算法获取。它用于捕捉局部领域的描述,包括曲率、主方向、次方向、法向量以及相应的特征值。为了实现上述,需要计算的协方差矩阵如下计算:
\[ \mathcal{M}=\frac{1}{k} \sum_{i=1}^{k}\left(p_{i}-\overline{p_{k}}\right)\left(p_{i}-\overline{p_{k}}\right)^{T} \]
其中,\(k\)表示总的点数,\(\bar{p_k}\)表示点集的均值。
进一步的,对协方差矩阵M执行了SVD分解,以获取特征值\(\lambda\)和特征向量\(v\)。可以通过协方差矩阵的特征向量来区分各种特征,这些特征向量与最显著的数据方差方向相关联。一些分散点主要根据特征值近似平等的方法来进行过滤。然后,点云的平坦度flatness和球面度sphericity[30]可以计算如下:
\[ \begin{aligned} \gamma &=\frac{\lambda_{3}}{\lambda_{1}+\lambda_{2}+\lambda_{3}} \\ \sigma &=\frac{\lambda_{2}-\lambda_{3}}{\lambda_{1}}, \quad \psi=\frac{\lambda_{3}}{\lambda_{1}} \end{aligned} \]
其中,
- \(\gamma\)是曲率
- \(\sigma\)是平坦度
- \(\psi\)是球面系数
- 需要注意的是,特征值以降序的顺序给出
如算法3展示,如果平坦度系数\(\sigma\)比平面特征阈值\(\tau\)更大,然后将点作为平面特征的垂直部分提取。对于非平面部分,如果球面系数\(\psi\)比球面特征阈值\(\pi\)更大,点将会添加到球面特征中。

来自HDL-64E激光雷达的不同特征的提取示意图如图6所示。

进一步的,主方向和法向量将会在后续残差计算中继续使用,以进一步细化水平和垂直分布的关联特征。