Trajectory modification considering dynamic constraints of autonomous robots

摘要
经典的“松紧带”使由全局规划器生成的路径相对于最短路径长度发生变形,为了避免与障碍物接触。它不直接考虑底层机器人的任何动态约束。本文贡献引入了一种名为“时间弹性带”的新方法,该方法明确地考虑了运动的时间方面的动态约束,如有限的机器人速度和加速度。“时间弹性带”问题用加权多目标优化框架表示。大多数目标是局部的,因为它们依赖于一些邻近的中间配置。这就得到了一个有效的大规模约束最小二乘优化方法存在的稀疏系统矩阵。
仿真和实际机器人的实验结果表明,该方法具有较好的鲁棒性和计算效率,能够实时生成最优机器人轨迹。“时间弹性带”将由一系列路径点组成的初始路径转换为明确依赖于时间的轨迹,从而实现对机器人的实时控制。由于其模块化的形式,该方法很容易扩展到包含额外的目标和约束。
介绍
在运动规划的背景下,本文侧重于局部路径修改,假设初始路径已由全局规划器生成[1]。特别是在服务机器人的环境中,由于动态环境可能是动态的,由于其固有的不确定性,修改路径是一种较好的方法。此外,由于局部、不完整的地图和动态障碍,环境模型可能会发生变化,此外,在实时应用中,大规模全局路径的(重新)计算往往是不可行的。这种观测结果导致了局部修改路径的方法,如[2,3]提出的“弹性带”,“松紧带”方法的主要思想是,将原来给定的路径视为受内外力影响的弹性橡皮筋,使其变形,而内外力相互平衡,使路径收缩,同时与障碍物保持一定距离。
后来这种方法被推广到非完整运动学[4,5,6]、多自由度[7]机器人系统和动态障碍[8],然而,据我们所知,动态运动约束还没有被认为是对路径变形的一个目标。典型的方法是用样条曲线平滑路径,获得动态可行轨迹。
我们的方法称为“时间弹性带”,是一种新颖的方法,因为它明确地增加了“弹性带”的时间信息,从而允许考虑机器人的动态约束和直接修改轨迹而不是路径。图1展示了使用时间弹性带架构的机器人系统:
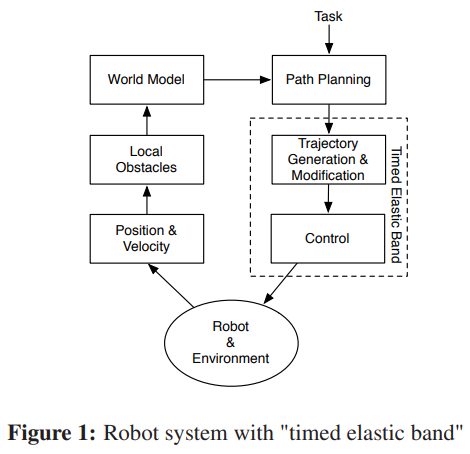
通过考虑时间信息,“时间弹性带”也可以用来控制机器人的速度和加速度,这个方法也适用于高维的状态空间,尽管本文只考虑了差分驱动机器人的平面环境移动,有三个全局自由度和两个局部自由度。
时间弹性带
经典的“弹性带”是用n个机器人的中间姿态序列来描述的,\(\mathbf{x}_{i}=\left(x_{i}, y_{i}, \beta_{i}\right)^{T} \in \R^{2} \times S^1\),下面记为位置(x_i,y_i)和旋转\(\beta_i\),如图2所示:
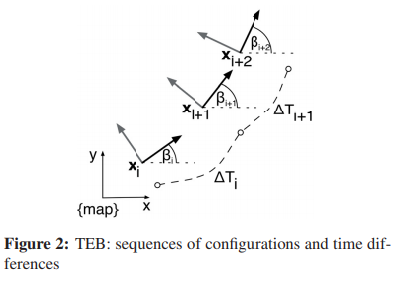
\[ Q=\left\{\mathbf{x}_{i}\right\}_{i=0 \ldots n} \quad n \in \mathbb{N} \]
TEB由两个连续的配置之间的时间间隔来进行时间调整,因此一个序列中包含\(n-1\)个\(\Delta T_i\):
\[ \tau=\left\{\Delta T_{i}\right\}_{i=0 \ldots n-1} \]
每个时间差表示机器人从一个配置依次过渡到下一个配置的时间(图2),因此TEB定义为元祖序列:
\[ B:=(Q, \tau) \]
其关键思想是通过实时加权多目标优化,在配置和时间间隔两个方面进行调整和优化:
\[ \begin{aligned} f(B) &=\sum_{k} \gamma_{k} f_{k}(B) \\ B^{*} &=\underset{B}{\operatorname{argmin}} f(B) \end{aligned} \]
其中,
- \(B*\)表示优化的TEB
- \(f(B)\)记为目标函数,在本文中由多个加权成分\(f_k\)组成,用于面对不同的方面,这是最基本的多目标优化方法,但它已经产生了非常好的结果。
目标函数的大部分分量相对于B是局部的,因为它们只依赖于几个连续的配置,而不是整个可配置空间带。
TEB的这种局部性导致了一个稀疏系统矩阵,为其提供了专门的快速有效的大规模数值优化方法[11]。
TEB的目标函数分为两类:
- 约束例如速度、加速度限制等惩罚项
- 目标项如最快、最短路径或者远离障碍等(等式8)
因此,在“时间弹性带”的背景下,这些约束被表述为一个分段连续、可微的代价函数的目标,该函数会惩罚违反约束的行为:
\[ e_{\Gamma}\left(x, x_{r}, \epsilon, S, n\right) \simeq \begin{cases}\left(\frac{x-\left(x_{r}-\epsilon\right)}{S}\right)^{n} & \text { if } x>x_{r}-\epsilon \\ 0 & \text { otherwise }\end{cases} \]
其中,
- \(x_r\)表示边界
- \(S,n,\epsilon\) 影响近似的准确性
- 特别的,\(S\)表示尺度缩放,\(n\)表示阶数,\(\epsilon\)是近似的一个位移小量
图3展示了等式6的两个不同的实现。 Approximation 1 (n = 2, S = 0.1, \(\epsilon\)= 0.1) , Approximation 2 (n = 2, S = 0.05 and \(\epsilon\) = 0.1) , 这个例子展示了约束\(x_r=0.4\)的一个近似。
使用多目标优化框架的一个明显优势是目标函数的模块化表达。目前TEB所采用的目标函数如下:
Way points and obstacles
TEB同时考虑原始路径的中间路径点的到达和避免静态或者动态的障碍物。这两个目标函数相似,不同之处在于点吸引橡皮筋,而障碍物排斥它。
目标函数企图最小化TEB和way point的距离\(d_{min,j}\),如图4所示:
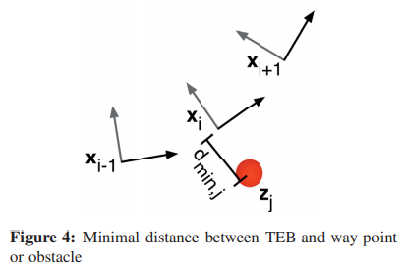
对于way point的情况,其距离以最大的目标半径\(r_{pmax}\)为界,这些约束由公式6中的惩罚函数实现:
\[ \begin{aligned} f_{\text {path }} &=e_{\Gamma}\left(d_{\min , j}, r_{p_{\max }}, \epsilon, S, n\right) \\ f_{o b} &=e_{\Gamma}\left(-d_{\min , j},-r_{o_{\min }}, \epsilon, S, n\right) \end{aligned} \]
由图3可知,必须将Eq. 8中\(d_{\min , j}\)和\(r_{o_{min}}\)交换符号来实现下界.
注意,这些目标函数的梯度可以解释为作用在弹性带上的外力
Velocity and acceleration
机器人速度和加速度的动力学约束用与几何约束相似的罚函数来描述,图2展示了TEB的结构,线速度和角速度的均值使用两个连续配置\(x_i,x_{i+1}\)之间的欧式距离和角距离和时间差\(\Delta T_i\)来计算:
\[ \begin{aligned} v_{i} & \simeq \frac{1}{\Delta T_{i}}\left\|\left(\begin{array}{l} x_{i+1}-x_{i} \\ y_{i+1}-y_{i} \end{array}\right)\right\| \\ \omega_{i} & \simeq \frac{\beta_{i+1}-\beta_{i}}{\Delta T_{i}} \end{aligned} \]
由于配置的临近,欧几里得距离是两个连续姿态之间的圆路径的真实长度的充分近似值。
加速度涉及两个连续的平均速度,因此考虑三个连续的构型,其中两个对应时间差:
\[ a_{i}=\frac{2\left(v_{i+1}-v_{i}\right)}{\Delta T_{i}+\Delta T_{i+1}} \]
为了清楚起见,用上式两个相关的速度来代替这三个连续的配置,旋转的加速度计算类似。
考虑一个差分驱动的移动机器人,轮速和位移\(v_i\)、旋转速度\(w_i\)关于机器人中心点的关系如下:
\[ \begin{aligned} v_{w_{r}, i} &=v_{i}+L \omega_{i} \\ v_{w_{l}, i} &=v_{i}-L \omega_{i} \end{aligned} \]
其中,L为机器人轮距的一半
将公式12和公式13(即上面两个式子)对时间进行微分就得到了相应的车轮加速度。车轮的速度和加速度是有界的,可根据制造商的规格获取。机器人的平移和转动惯量可以以一种明显的方式包括在内,但在这第一个实现中,我们还没有这样做。
Non-holonomic kinematics(非完整约束运动学方程)
差动驱动的机器人只有两个局部自由度,因此,它们只能在机器人当前航向的方向执行运动,这种运动学约束导致了由圆弧段组成的平滑路径。
因此,两个相邻的构型需要位于一个常曲率的公共圆弧上,如图5所示

初始配置\(x_i\)和方向\(d_{i,i+1}\)之间的角度\(\vartheta_{i}\)必须等于配置\(x_{i+1}\)和方向\(d_{i,i+1}\)之间的夹角,即:
\[ \vartheta_{i}=\vartheta_{i+1} \]
根据二维叉积(\(A \times B=|A|·|B|·\sin \alpha\)),有:
\[ \Leftrightarrow\left(\begin{array}{c} \cos \beta_{i} \\ \sin \beta_{i} \\ 0 \end{array}\right) \times \mathbf{d}_{i, i+1}=\mathbf{d}_{i, i+1} \times\left(\begin{array}{c} \cos \beta_{i+1} \\ \sin \beta_{i+1} \\ 0 \end{array}\right) \]
其中,机器人的绝对旋转为\(\beta_i\),位移方向向量为:
\[ \mathbf{d}_{i, i+1}:=\left(\begin{array}{c} x_{i+1}-x_{i} \\ y_{i+1}-y_{i} \\ 0 \end{array}\right) \]
因此,对应的目标函数为:
\[ f_{k}\left(\mathbf{x}_{i}, \mathbf{x}_{i+1}\right)=\left\|\left[\left(\begin{array}{c} \cos \beta_{i} \\ \sin \beta_{i} \\ 0 \end{array}\right)+\left(\begin{array}{c} \cos \beta_{i+1} \\ \sin \beta_{i+1} \\ 0 \end{array}\right)\right] \times \mathbf{d}_{i, i+1}\right\|^{2} \]
惩罚违反此约束的二次误差。一个潜在的180方向的变化用一个额外的项来处理
Fastest path
以往的“松紧带”方法通过收缩松紧带的内力获得最短路径。由于我们的方法考虑时间信息作为最短路径的目标,我们可以选择用最快路径的目标代替最短路径的目标,或者将这些目标结合起来。
最快路径的目标很容易通过最小化所有时间差的和的平方来实现:
\[ f_{k}=\left(\sum_{i=1}^{n} \Delta T_{i}\right)^{2} \]
这一目标导致了一种最快的路径,其中中间配置在时间上均匀分离,而不是在空间上
实现
图6展示了实现TEB的控制流程,在初始化阶段,初始路径被增强为初始轨迹,方法是根据动力学和运动学约束添加默认的时间信息。
在我们的例子中,初始轨迹是由带有纯旋转和平移的分段线性分段组成的,这种以多边形表示的路径通常由概率路线图规划者提供[9],另外,reed - shepp路径很容易被增强为允许的轨迹[10]。
在每一次迭代中,算法动态地添加新的结构或删除以前的结构,以调整空间和时间分辨率以适应剩余的轨迹长度或规划水平。
一个滞后被实施以避免振荡。将优化问题转化为一个超图,用包含在“g20 -框架”中的大规模稀疏系统优化算法求解[11]

所要求的超图是一条边的连接节点数量不受限制的图,因此,一条边可以连接两个以上的节点。
TEB问题(Eq. 4)可以转化为一个以配置和时间差为节点的超图。它们与表示给定目标函数fk或约束函数的边相连,图7展示了一个两配置一个时间差和一个点状障碍物的超图,
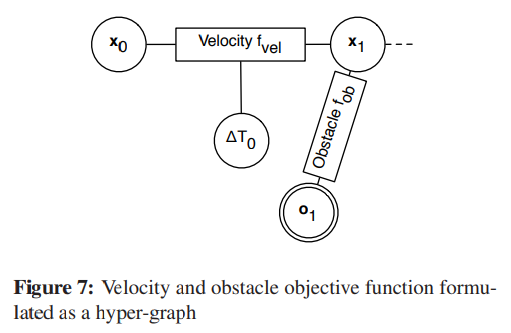
速度边界目标函数要求的平均速度与两个配置之间的欧氏距离和所需的时间有关。因此它形成一条连接B的那些状态的边。
障碍物需要一条与最近的配置相连的边,表示障碍物的节点是固定的(双圆),因此优化算法无法改变其参数(位置)
在验证优化后的TEB后,可以通过计算控制变量v和ω来直接命令机器人驱动系统。
在每一次新的迭代之前,重新初始化阶段将检查新的和变化的way-points,这将会比较有用如果way-points是在分析相机或者激光数据之后才收到的。