FAST-LIO2: Fast Direct LiDAR-inertial Odometry

摘要
在高效的紧密耦合迭代卡尔曼滤波器上,FAST-LiO2有两个关键的新科技,可允许快速,强大,准确的LIDAR导航(和建图)。
- 直接将原始点注册到地图(随后更新地图)而不提取特征点。这使得能够利用环境中的微妙特征,因此提高了准确性。取消手工设计的特征提取模块也使其自然适应不同扫描模式的新兴 LiDAR。
- 第二个主要新颖性是通过增量K-D树数据结构,来维护地图,该映射可以增量更新(即点插入,删除)和动态重新平衡。与现有的动态数据结构相比(Octree,R * -tree,Nanoflann K-D树),IKD-Tree实现了卓越的整体性能,同时支持基于数的降采样
我们在来自各种开放式LIDAR数据集中的19个序列中进行详尽的基准比较,与其他最先进的 LiDAR 惯性导航系统相比,FAST-LIO2 以更低的计算负载持续实现更高的精度,还进行了关于具有小FOV的固态激光雷达的各种真实实验。
总的来说,FAST-LiO 2是计算上有效的(例如,高达100 Hz的里程计和大型环境中的建图),鲁棒(例如,杂乱的室内环境中具有旋转的杂乱的室内环境的可靠姿态估计,多功能(即, 适用于多线和固态LIDARS,UAV和手持平台,英特尔和基于ARM的处理器),同时仍然比现有方法实现更高的准确性。
介绍
我们开发一个增量K-D树数据结构,IKD树,有效地表示大规模稠密点云地图。 除了有效的最近邻搜索之外,新的数据结构还支持增量地图更新(即,点插入,基于数的降采样,点删除)和最小计算成本的动态重新平衡。
这些功能使IKD树非常适合基于激光雷达的里程计和建图应用,在计算限制平台上实现100 Hz 里程计和建图,如微型UAV板载计算机(英特尔I7)甚至基于ARM的处理器。
通过增加IKD树的计算效率允许,我们直接将原始点注册到地图,即使具有激进的运动和非常杂乱的环境,也能够更准确和可靠的扫描配准。我们将此使用原始点的配准称为类似于Visual Slam的直接方法[21]。消除手工工程特征提取使得系统自然适用于不同的激光雷达传感器。
我们将以上两个改进整合到先前的工作FAST-LIO中,该系统使用IMU通过严格的反向传播步骤来遵从每个点的运动,并通过迭代扩展卡尔曼滤波器估计系统的完整状态。为了进一步加速计算,使用新的和数学上等同的计算卡尔曼增益的公式用于将计算复杂性降低到状态的维度(而不是观测的维度)。
新的系统称为FAST-LIO2,关于各种尺寸的18个序列的实验表明,IKD树在应用激光雷达测量和测绘时实现了相比于现有动态数据结构(Octree,R * -Tree,Nanoflann K-D树)的卓越性能
系统概述
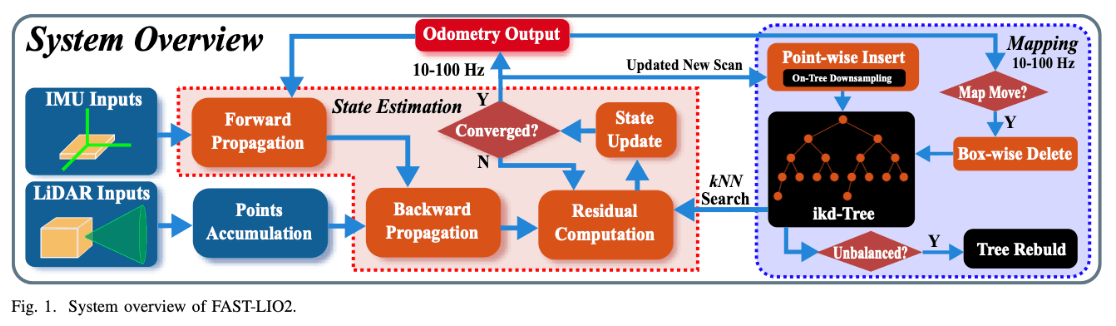
FAST-LIO2的数据流如图所示,为了执行状态估计,新扫描中的点被通过紧密耦合的迭代卡尔曼滤波器框架(有红色的大虚线块)注册到大型局部地图中。大型局部地图中的全局地图点由增量K-D树结构IKD-Tree组织(蓝色虚线块)。如果当前LIDAR的FOV范围交叉地图边界,则将删除IKD树中,从LIDAR位置到最远地图区域中的历史点。
结果,IDK-TREE跟踪在一个大范围立方体区域(map size)中的所有地图点,并用于计算状态估计模块中的残差。优化后的位姿最后将新扫描中的点注册到全局坐标系,并通过以里程计频率插入到IKD树,来将它们合并到地图中。
状态估计
FAST-LIO2的状态估计是从FAST-LIO[22]继承的,且进一步整合了Lidar-IMU的外参在线标定。在这里,我们简要解释滤波器的基本配方和工作流程,并参考[22]了解更多细节。
系统模型
我们首先导出系统模型,由状态转换模型和测量模型组成
状态转移模型
取第一个 IMU 帧(记为 I)作为全局帧(记为 G),记\({ }^{I} \mathbf{T}_{L}=\left({ }^{I} \mathbf{R}_{L},{ }^{I} \mathbf{p}_{L}\right)\)为激光雷达到IMU的外参(未知),那么模型如下:
\[ \begin{aligned} { }^{G} \dot{\mathbf{R}}_{I} &={ }^{G} \mathbf{R}_{I}\left\lfloor\boldsymbol{\omega}_{m}-\mathbf{b}_{\boldsymbol{\omega}}-\mathbf{n}_{\boldsymbol{\omega}}\right\rfloor_{\wedge}\\ { }^{G} \dot{\mathbf{p}}_{I} &={ }^{G} \mathbf{v}_{I} \\ { }^{G} \dot{\mathbf{v}}_{I} &={ }^{G} \mathbf{R}_{I}\left(\mathbf{a}_{m}-\mathbf{b}_{\mathbf{a}}-\mathbf{n}_{\mathbf{a}}\right)+{ }^{G} \mathbf{g} \\ \dot{\mathbf{b}}_{\boldsymbol{\omega}} &=\mathbf{n}_{\mathbf{b} \omega}, \dot{\mathbf{b}}_{\mathbf{a}}=\mathbf{n}_{\mathbf{b a}} \\ { }^{G} \dot{\mathbf{g}} &=\mathbf{0},{ }^{I} \dot{\mathbf{R}}_{L}=\mathbf{0},{ }^{I} \dot{\mathbf{p}}_{L}=\mathbf{0} \end{aligned} \]
其中,
- \({ }^{G} \mathbf{p}_{I},{ }^{G} \mathbf{R}_{I}\)分别为全局坐标系下的IMU的位置和姿态
- \({ }^{G} \mathbf{g}\)是全局坐标系下的重力向量
- \(\mathbf{a}_{m}\),\(\omega_{m}\)是IMU测量
- \(\mathbf{b}_{\mathbf{a}}\),\(\mathbf{b}_{\boldsymbol{\omega}}\)是由噪声\(\mathbf{n}_{\mathbf{b a}},\mathbf{n}_{\mathbf{b \omega}}\)驱动的随机游走过程建模的IMU偏置
- \(\lfloor\mathbf{a}\rfloor_{\wedge}\)表示由向量\(\mathbf{a}\)构成的反对称矩阵
记\(i\)为IMU测量的索引,基于[22]中定义的\(\boxplus\) 操作符,连续时间下的动态模型可以根据IMU采样周期\(\Delta t\)进行离散化,如下:
\[ \mathbf{x}_{i+1}=\mathbf{x}_{i} \boxplus \left(\Delta t \mathbf{f}\left(\mathbf{x}_{i}, \mathbf{u}_{i}, \mathbf{w}_{i}\right)\right) \]
其中,函数\(\mathbf{f}\),状态\(\mathbf{x}\),输入\(\mathbf{u}\)和噪声\(\mathbf{w}\)定义如下:
\[ \mathcal{M} \triangleq S O(3) \times \mathbb{R}^{15} \times S O(3) \times \mathbb{R}^{3} ; \operatorname{dim}(\mathcal{M})=24 \]
\[ \mathbf{x} \triangleq\left[\begin{array}{llllllll} { }^{G} \mathbf{R}_{I}^{T} & { }^{G} \mathbf{p}_{I}^{T} & { }^{G} \mathbf{v}_{I}^{T} & \mathbf{b}_{\boldsymbol{\omega}}^{T} & \mathbf{b}_{\mathbf{a}}^{T} & { }^{G} \mathbf{g}^{T} & { }^{I} \mathbf{R}_{L}^{T} & { }^{I} \mathbf{p}_{L}^{T} \end{array}\right]^{T} \in \mathcal{M} \]
\[ \mathbf{u} \triangleq\left[\begin{array}{ll} \boldsymbol{\omega}_{m}^{T} & \mathbf{a}_{m}^{T} \end{array}\right]^{T} \]
\[ \mathbf{w} \triangleq\left[\begin{array}{llll} \mathbf{n}_{\boldsymbol{\omega}}^{T} & \mathbf{n}_{\mathbf{a}}^{T} & \mathbf{n}_{\mathbf{b} \boldsymbol{\omega}}^{T} & \mathbf{n}_{\mathbf{b a}}^{T} \end{array}\right]^{T} \]
\[ \mathbf{f}(\mathbf{x}, \mathbf{u}, \mathbf{w})=\left[\begin{array}{c} \boldsymbol{\omega}_{m}-\mathbf{b}_{\boldsymbol{\omega}}-\mathbf{n}_{\boldsymbol{\omega}} \\ { }^{G} \mathbf{v}_{I}+\frac{1}{2}\left({ }^{G} \mathbf{R}_{I}\left(\mathbf{a}_{m}-\mathbf{b}_{\mathbf{a}}-\mathbf{n}_{\mathbf{a}}\right)+{ }^{G} \mathbf{g}\right) \Delta t \\ { }^{G} \mathbf{R}_{I}\left(\mathbf{a}_{m}-\mathbf{b}_{\mathbf{a}}-\mathbf{n}_{\mathbf{a}}\right)+{ }^{G} \mathbf{g} \\ \mathbf{n}_{\mathbf{b} \omega} \\ \mathbf{n}_{\mathbf{b a}} \\ \mathbf{0}_{3 \times 1} \\ \mathbf{0}_{3 \times 1} \\ \mathbf{0}_{3 \times 1} \end{array}\right] \in \mathbb{R}^{24} \]
量测模型
LIDAR通常是一个接一个地点的样品。 因此,当激光雷达经历连续运动时,所得到的点在不同的姿势处采样,为了纠正这种扫描运动,我们采用[22]中提出的反向传播,其估计每个激光点时刻下的激光雷达位姿相对于该帧激光扫描最后时刻的激光雷达位姿。估计的相对姿势使我们能够基于扫描中每个单独点的精确采样时间将所有点投影到扫描结束时间,以实现校正。
记\(k\)为激光扫描的索引,\(\{ { }^{L} \mathbf{p}_{j}, j = 1,\dots,m\}\)是第\(k\)帧激光坐标系下的激光点(扫描结束时刻),由于激光测量存在噪声,每一个点\(\mathbf{p}_{j}\)都会受到由测距和方向组合的噪声项\({ }^{L} \mathbf{n}_{j}\)影响。因此,真正的激光点与测量值之间存在如下关系:
\[ { }^{L} \mathbf{p}_{j}^{\mathrm{gt}}={ }^{L} \mathbf{p}_{j}+{ }^{L} \mathbf{n}_{j} \]
真正的激光点\({ }^{L} \mathbf{p}_{j}^{\mathrm{gt}}\),根据对应的激光雷达位姿\({ }^{\mathbf{G}}\mathbf{T}_{I_{k}}=\left({ }^{G} \mathbf{R}_{I_{k}},{ }^{G} \mathbf{p}_{I_{k}}\right)\)以及外参\({ }^{I} \mathbf{T}_{L}\)进行坐标转换,其应该准确的位于地图中的局部的平面上,满足:
\[ \mathbf{0}={ }^{G} \mathbf{u}_{j}^{T}\left({ }^{G} \mathbf{T}_{I_{k}}{ }^{I} \mathbf{T}_{L}\left({ }^{L} \mathbf{p}_{j}+{ }^{L} \mathbf{n}_{j}\right)-{ }^{G} \mathbf{q}_{j}\right) \]
其中,
- \({ }^{G} \mathbf{u}_{j}\)是对应关联平面的法向量
- \({ }^{G} \mathbf{q}_{j}\)是平面上的点
- 值得注意的是,\({ }^{G} \mathbf{T}_{I_{k}},{ }^{I} \mathbf{T}_{L}\)都包含在状态向量\(\mathbf{x}_k\)中
因此,第\(j\)个点的测量\({ }^{L} \mathbf{p}_{j}\),可以写成统一紧凑形式如下:
\[ \mathbf{0}=\mathbf{h}_{j}\left(\mathbf{x}_{k},{ }^{L} \mathbf{p}_{j}+{ }^{L} \mathbf{n}_{j}\right) \]
这定义了状态矢量\(\mathbf{x}_k\)的隐式测量模型
迭代卡尔曼滤波器
基于上面的状态模型和基于流形\(\mathcal{M} \triangleq S O(3) \times \mathbb{R}^{15} \times S O(3) \times \mathbb{R}^{3}\)的量测模型,我们使用迭代卡尔曼滤波器直接在流形\(\mathcal{M}\)上进行操作,遵循文献[55][22]。
其包含两个关键步骤:
- 在每个IMU测量上传播
- 在每一帧激光扫描上进行迭代
这两个步骤都自然地估计流形\(\mathcal{M}\)上的状态,从而避免了renormalization。
1)传播
假设最优状态估计在融合完最后一帧(如\(k-1\)帧)激光扫描后的状态为\(\overline{\mathbf{x}}_{k-1}\),且协方差矩阵为\(\overline{\mathbf{P}}_{k-1}\),前向传播是在IMU测量到达时进行的,更具体地说,通过将过程噪声\(\mathbf{w}_i\)设置为零,状态和协方差将按照状态转移模型进行传播: