FAST-LIO: A Fast, Robust LiDAR-inertial Odometry Package by Tightly-Coupled Iterated Kalman Filter

摘要
方法
架构总览
本文使用的符号如表一所示

系统的流图如图2所示
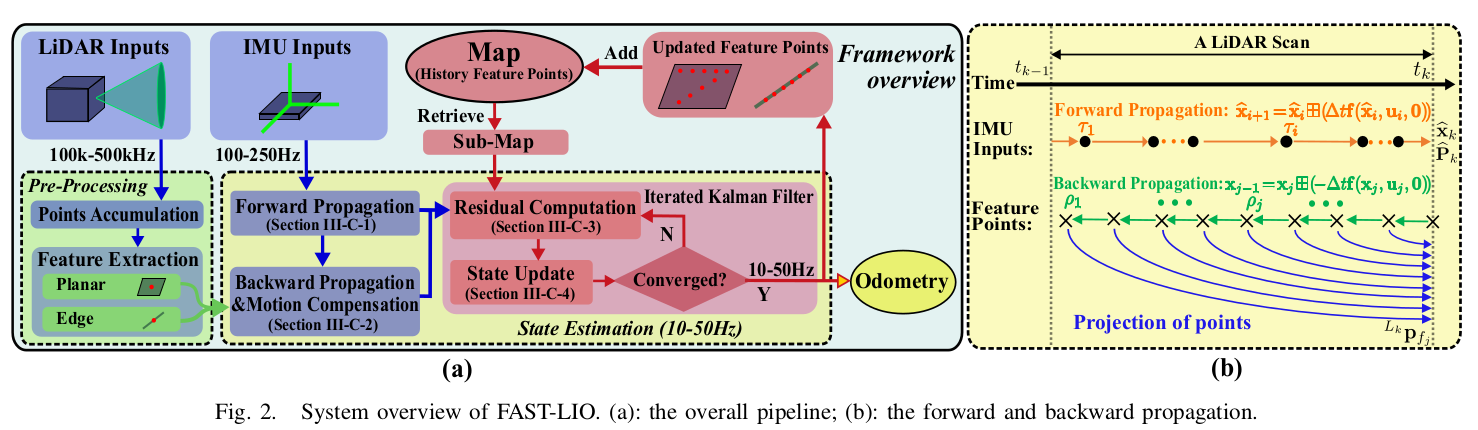
将激光雷达输入输入特征提取模块,获取平面和边缘特征。然后将提取的特征和IMU测量值输入状态估计模块进行10Hz和50Hz的状态估计。然后,估计的姿态将特征点注册到全局坐标系,并将它们与到目前为止建立的特征点地图合并,最后,在下一步中使用更新后的特征地图来注册更多的新点。
系统描述
操作符
设M为考虑维度n的流形(如: \(\mathcal{M}=S O(3)\)),因为流形对于\(\mathbb{R}^{n}\)是局部homeomorphic的,因此我们可以建立双向的映射,即通过操作符\(\boxplus,\boxminus\)[23],从流形 \(\mathcal{M}\)的局部邻域映射到其正切空间\(\mathbb{R}^{n}\):
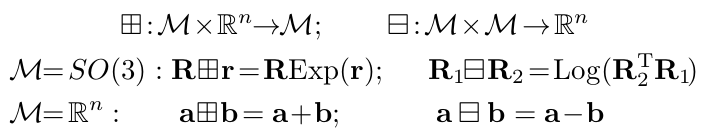
其中,\(\operatorname{Exp}(\mathbf{r})=\mathbf{I}+\frac{\mathbf{r}}{\|\mathbf{r}\|} \sin (\|\mathbf{r}\|)+\frac{\mathbf{r}^{2}}{\|\mathbf{r}\|^{2}}(1-\cos (\|\mathbf{r}\|))\)是指数映射[23],\(\log (\cdot)\)则是其逆映射。对于组合的流形\(\mathcal{M}=S O(3) \times \mathbb{R}^{n}\),我们有:
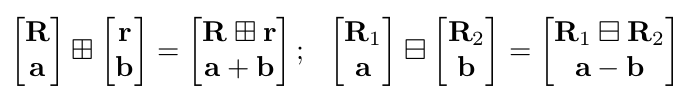
利用上述定义,我们可以得到:
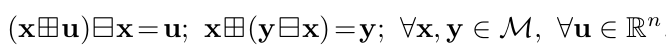
连续时间模型
假设IMU与激光雷达之间是刚体变换,其中外参是\({ }^{I} \mathbf{T}_{L}=\left({ }^{I} \mathbf{R}_{L},{ }^{I} \mathbf{p}_{L}\right)\)。以IMU坐标系(记为\(I\))作为body坐标系,可得运动学模型:
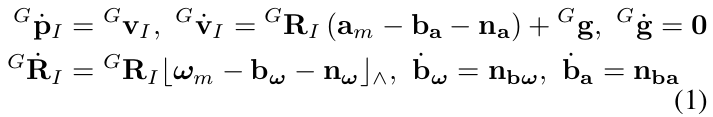
其中,
- \({ }^{G} \mathbf{p}_{I},{ }^{G} \mathbf{R}_{I}\)分别是IMU在全局坐标系(如第一帧IMU坐标系,记为\(G\))的位置和姿态。
- \({ }^{G} \mathbf{g}\)是全局坐标系下未知的重力向量
- \(\mathbf{a}_{m}\),\(\boldsymbol{\omega}_{m}\)是IMU测量
- \(\mathbf{n}_{\mathbf{a}}\) and \(\mathbf{n}_{\boldsymbol{\omega}}\)是IMU测量白噪声
- \(\mathbf{b}_{\mathbf{a}}\) and \(\mathbf{b}_{\boldsymbol{\omega}}\)是由高斯噪声\(\mathbf{n}_{\mathbf{b a}}\) , \(\mathbf{n}_{\mathbf{b} \omega}\)随机游走过程建模的bias
- \(\lfloor\mathbf{a}\rfloor_{\wedge}\)表示向量\(\mathbf{a} \in \mathbb{R}^{3}\)的反对称矩阵
离散时间模型
基于上面的\(\boxplus\)操作符,我们在IMU采样周期\(\Delta t\)内使用零阶保持器来对式(1)的连续时间模型进行离散化,得到:
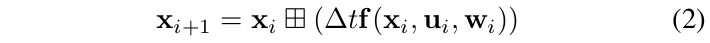
其中,i表示IMU测量的索引,函数\(\mathbf{f}\),状态\(\mathbf{x}\),输入\(\mathbf{u}\),噪声\(\mathbf{w}\)定义如下:
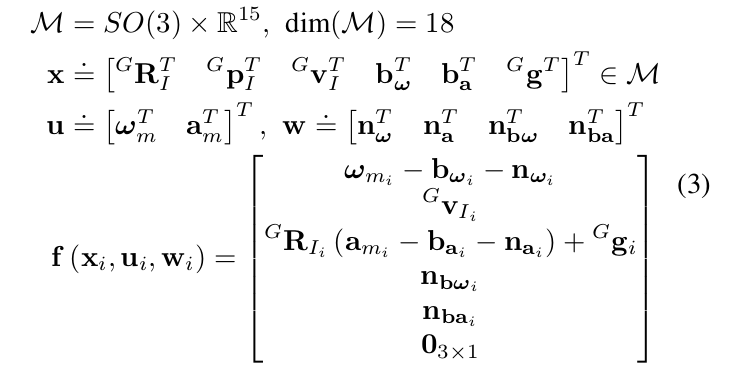
激光测量预处理
激光雷达测量是点坐标在它的局部坐标系。由于原始激光雷达点的采样速率非常高(例如,200kHz),通常不可能在接收到每个新点后马上进行处理,一种更实际的方法是在一段时间内积累这些点,然后一次性处理它们。
FAST-LIO中,最小积累间隔设置为20毫秒,可产生高达50 Hz的全状态估计(即里程计输出)和地图更新,如图2 (a)所示。这种累积的点集称为scan,其处理时间记为\(t_k\)(见图2 (b)。
我们从原始点中提取局部光滑度高的平面点[8]和局部光滑度低的边缘点[10],假设特征点的数量为m,每个特征点在\(\rho_{j} \in\left(t_{k-1}, t_{k}\right]\)时刻采样,特征点记为\({ }^{L_{j}} \mathbf{p}_{f_{j}}\),其中\(L_{j}\)是\(\rho_{j}\)时刻下激光雷达坐标系。
在激光扫描期间,通常会收到几帧IMU测量,假设每一个IMU采样时间\(\tau_{i} \in\left[t_{k-1}, t_{k}\right]\),其对应的状态\(\mathbf{x}_i\)如式(2)。注意,最后一个激光雷达特征点是扫描的结束,即\(\rho_{m}=t_{k}\),而IMU测量值不一定与扫描开始或结束时对齐。
状态估计
为了估计状态公式(2)中的状态,我们使用了迭代扩展卡尔曼滤波器,此外,我们刻画了状态估计的正切空间中的估计协方差,如[23,24]。
假设在\(t_{k-1}\)时刻下最后一次激光雷达扫描的最佳状态估计为\(\bar{\mathbf{x}}_{k-1}\),协方差为\(\overline{\mathbf{P}}_{k-1}\)。其中,\(\overline{\mathbf{P}}_{k-1}\)代表了如下误差状态向量的协方差:
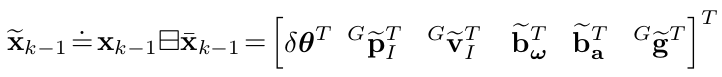
其中,
- \(\delta \boldsymbol{\theta}=\log \left({ }^{G} \overline{\mathbf{R}}_{I}^{T G} \mathbf{R}_{I}\right)\)是姿态误差
- 剩下的其他都是直接相减
直觉的,\(\delta \boldsymbol{\theta}\)描述了姿态真值和估计值之间的小偏差,使用这个来定义姿态误差的好处是允许使用3x3协方差矩阵\(\mathbb{E}\left\{\delta \boldsymbol{\theta} \delta \boldsymbol{\theta}^{T}\right\}\)来描述姿态的不确定性。因为姿态是3自由度,因此这是最小表达。
1)前向传播
一旦接收到IMU输入,则执行一次前向传播(如图2所示),特别的,前向传播根据式(2)进行,且把噪声\(\mathbf{W}_{i}\)设置为零,(相当于nominal state):
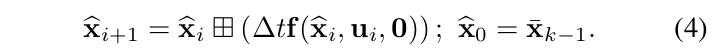
其中,\(\Delta t=\tau_{i+1}-\tau_{i}\),为了传播协方差,我们使用下面的误差状态动态模型:
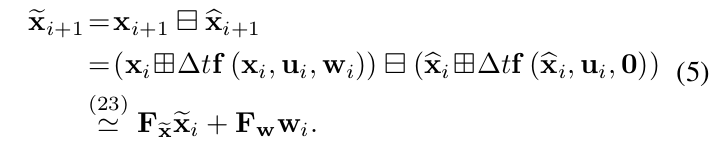
矩阵\(\mathbf{F}_{\widetilde{\mathbf{x}}}\)和\(\mathbf{F}_{\mathbf{w}}\)为误差状态模型(实际上就是误差分析,可参考博客),具体计算见附录A.
此处直接给出结果:

其中,
- \(\widehat{\boldsymbol{\omega}}_{i}=\boldsymbol{\omega}_{m_{i}}-\widehat{\mathbf{b}}_{\boldsymbol{\omega}_{i}}\)
- \(\widehat{\mathbf{a}}_{i}=\mathbf{a}_{m_{i}}-\widehat{\mathbf{b}}_{\mathbf{a}_{i}}\)
且\(\mathbf{A}(\mathbf{u})^{-1}\)遵循[25]中的定义,如下计算:
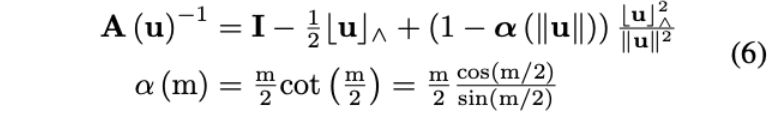
记白噪声\(\mathbf{w}\)的协方差为Q,然后可以通过下式来迭代传播协方差\(\widehat{\mathbf{P}}_{i}\):
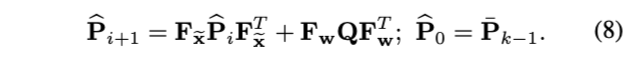
前向传播直到新的一帧数据结束\(t_k\),传播的状态和协方差分别记为\(\widehat{\mathbf{x}}_{k}, \widehat{\mathbf{P}}_{k}\),协方差表示状态真值与传播值之间的误差协方差。
2)反向传播和运动补偿
当在时间\(t_k\),新一帧的特征点应该与传播状态\(\widehat{\mathbf{x}}_{k}\)和协方差\(\widehat{\mathbf{P}}_{k}\)进行结合以产生最优状态更新。然而,尽管新的一帧是在\(t_k\)到达,实际上特征点是在各自的采样时刻\(\rho_j\)下得到的,因此要进行运动畸变矫正。
为了补偿\(\rho_j\)到\(t_k\)之间的相对运动(即运动畸变),根据式(2),可得传播方程\(\check{\mathbf{x}}_{j-1}=\check{\mathbf{x}}_{j}\) 田 \(\left(-\Delta t \mathbf{f}\left(\check{\mathbf{x}}_{j}, \mathbf{u}_{j}, \mathbf{0}\right)\right)\)。
向后传播在特征点的频率下执行,这通常远高于IMU速率,对于在两个IMU测量之间采样的所有特征点,我们使用左IMU测量作为后传播中的输入。
此外,注意到\(\mathbf{f}\left(\mathbf{x}_{j}, \mathbf{u}_{j}, \mathbf{0}\right)\)中最后三个块元素(对应于gyro bias,accelerometer bias和外参)都是零,因此,反向传播可以简化为:
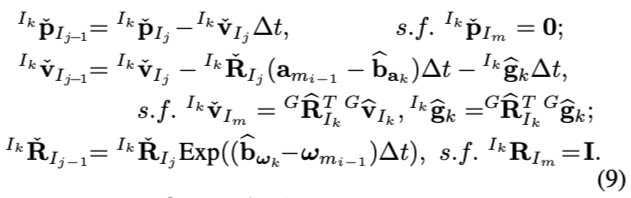
其中,
- \(\rho_{j-1} \in\left[\tau_{i-1}, \tau_{i}\right)\)表示一帧扫描内的某个时刻
- \(\Delta t=\rho_{j}-\rho_{j-1}\)表示两个点之间的时间差
- \(s.f.\)表示“starting form”的意思
反向传播会计算出时间\(\rho_{j}\)到时间\(t_k\) 的相对位姿变换\({ }^{I_{k}} \check{\mathbf{T}}_{I_{j}}=\left({ }^{I_{k}} \check{\mathbf{R}}_{I_{j}},{ }^{I_{k}} \check{\mathbf{p}}_{I_{j}}\right)\),这个相对位姿变换运行我们将激光扫描观测点\({ }^{L_{j}} \mathbf{p}_{f_{j}}\)投影到扫描结束时刻下的坐标系,如下:
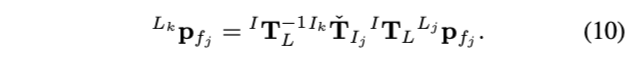
其中,\({ }^{I} \mathbf{T}_{L}\)是已知外参,投影点\({ }^{L_{k}} \mathbf{p}_{f_{j}}\)用于下一步构造残差。
3)残差计算
使用式(10)的运动补偿,我们可以看到在\(t_k\)时刻下所有特征点\(\left\{ { }^{L_{k}} \mathbf{p}_{f_{j}}\right\}\)正确的位置,并且用来构造残差。
假设当前IEKF迭代为\(\kappa\),对应的状态估计为\(\widehat{\mathbf{x}}_{k}^{\kappa}\)。当\(\kappa=0\),\(\widehat{\mathbf{x}}_{k}^{\kappa}=\widehat{\mathbf{x}}_{k}\),预测的状态即为式(4)传播的状态。因此,特征点可以被投影到全局坐标系,如下:

对于每一个激光特征点,假设其附近的附近特征点定义的最接近的平面或边缘是与之关联的特征。残差即为特征点与关联特征(平面、边缘)的欧式距离(全局坐标系下)。
记\(\mathbf{u}_{j}\)为平面法向量或者边缘方向,对于根据状态估计投影到全局坐标系的特征点\({ }^{G} \widehat{\mathbf{p}}_{f_{j}}^{\kappa}\),假设平面/边缘上有点\({ }^{G} \mathbf{q}_{j}\),残差\(\mathbf{z}_{j}^{\kappa}\)如下计算:
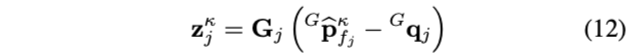
其中,
- \(\mathbf{G}_{j}=\mathbf{u}_{j}^{T}\)是平面特征
- \(\mathbf{G}_{j}=\left\lfloor\mathbf{u}_{j}\right\rfloor_{\wedge}\)是边缘特征
- \(\mathbf{u}_{j}\)的计算和最近邻点的搜索是通过构建局部地图KD-TREE来实现的
- 此外,我们只考虑
norm低于某些阈值(例如,0.5米)的残差。 超过此阈值的残差是异常值或新观察点