Kalman Filters on Differentiable Manifolds

摘要
卡尔曼滤波是现代控制系统中最重要和应用最广泛的滤波技术之一。然而,几乎所有当前的卡尔曼滤波器的变体都是在欧几里得空间Rn中制定的,而许多现实世界的系统(例如,机器人系统)实际上是在流形上进化的。
在本文中,我们提出了一种为这类流形上系统设计卡尔曼滤波器的方法。利用运算\(\boxplus \backslash \boxminus\),并进一步定义了相应流形上的⊕运算,给出了流形上系统的规范表示。这种非正则形式使我们能够在卡尔曼过滤的每一步中将多种约束从系统行为中分离出来,最终产生一个在流形上自然演化的通用的和象征性的卡尔曼过滤框架。
此外,这种流形上的卡尔曼滤波器集成了C++包实现,它使用户能够实现集成卡尔曼滤波器,就像在\(\mathbb{R}^{n}\)空间中的普通卡尔曼过滤一样:用户只需要提供系统特定的描述,然后调用各自的过滤步骤(例如,预测、更新),而不需要处理任何流形约束。
PRELIMINARIES OF DIFFERENTIABLE MANIFOLDS
可微分流形(Differentiable manifolds)
如文[34]所示,维数为n的流形是局部同胚于\(\mathbb{R}^{n}\)的集合M(称为homeomorphicspace)。、
也就是说,对于任意一个点\(\mathbf{x} \in \mathcal{M}\)以及一个包含该点的开子集\(U \subset \mathcal{M}\),存在一个双射函数(称为homeomorphism)φ,它将\(U\)中的点映射到\(\mathbb{R}^{n}\)的开子集。该对\((\phi, U)\)称为局部坐标图,如果任何两个图\((\phi, U)\)和\((\psi, V)\)共享重叠的合成映射\(\phi \circ \psi^{-1}\)是可微的,则该流形称为可微流形。
\(\boxplus \backslash \boxminus\)操作
流形M中任意点周围homeomorphisms的存在使我们能够封装两个算子\(\boxplus_{\mathcal{M}}\)(“boxplus”)和\(\boxminus_{\mathcal{M}}\)(“boxminus”)到流形[25]:
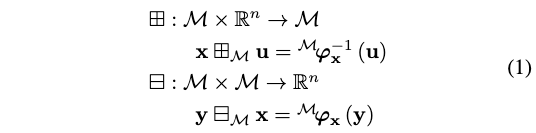
其中,\(\mathcal{M}_{\varphi_{\mathrm{x}}}\)是点\(\mathbf{x} \in \mathcal{M}\)的一个homeomorphism.
\(\mathbf{y}=\mathbf{x} \boxplus_{\mathcal{M}} \mathbf{u}\)的物理含义是向点\(\mathbf{x} \in \mathcal{M}\)添加一个扰动\(\mathbf{u}\),然后产生了流形上的\(\mathbf{y} \in \mathcal{M}\), 如图2所示。

其中,逆操作\(\mathbf{u}=\mathbf{y} \boxminus_{\mathcal{M}} \mathbf{x}\)可以确定扰动量\(\mathbf{u}\),该扰动量\(\mathbf{u}\)就是产生\(\mathbf{y} \in \mathcal{M}\)时,对点\(\mathbf{x} \in \mathcal{M}\)进行\(\boxplus_{\mathcal{M}^{-}}\)操作所添加的扰动。
这两个操作符创建了一个局部的、矢量化视角,对应于流形上复杂的全局结构。
对于李群来说,当\(\mathcal{M}\)是Lie group (e.g., \(\left.\mathbb{R}^{n}, S O(3), S E(3)\right)\),正切空间具有表示为m的李代数结构和指数映射\(\exp : \mathfrak{m} \mapsto \mathcal{M}\)。
令\(\mathfrak{f}: \mathbb{R}^{n} \mapsto \mathfrak{m}\)作为从最小参数化空间到李代数、指数映射\(\operatorname{Exp}=\exp \circ f\)以及其逆操作\(\log\)的的映射,那么\(\boxplus \backslash \boxminus\)操作的定义如下:
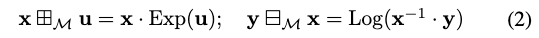
其中·是M上的二元运算,使得\((\mathcal{M}, \cdot)\)形成李群,\(\mathbf{x}^{-1}\)是\(\mathbf{X}\)的逆,对于李群上的元素,它总是存在。
当流形M不是李群时,找出流形与其切空间参数化之间的同胚没有一般准则。例如,2球面流形\(\mathbb{S}^{2}(r) \triangleq\{\mathbf{x} \in \left.\mathbb{R}^{3} \mid\|\mathbf{x}\|=r, r>0\right\}\)在点x处的切线空间就是在点\(\mathbf{X}\)的简单正切平面,如图3所示。



对于点\(\mathbf{x} \in \mathbb{S}^{2}(r)\),扰动可以通过沿着正切平面上的向量旋转来实现,结果仍将保留在\(\mathbb{S}^{2}(r)\)上。
正切平面中的旋转向量被\(\mathbf{u} \in \mathbb{R}^{2}\)最小参数化表达,其中,所在的空间为由两个bias向量\(\mathbf{b}_{1}, \mathbf{b}_{2} \in \mathbb{R}^{3}\)所展开的正切平面。也就是说:
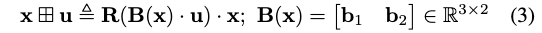
其中,\(\mathbf{R}(\mathbf{w})=\operatorname{Exp}(\mathbf{w}) \in S O(3)\)记为关于由向量\(\mathbf{w} \in \mathbb{R}^{3}\)所表示的轴-角旋转。特别的,\(\mathbf{b}_{1}, \mathbf{b}_{2}\)的选择不是唯一的,只要它们是正交的并且都垂直于x。
\(\mathbb{S}^{2}\)常用于重力的表示,如VINS-Mono就用这个来表示并进一步refine重力向量。
\(\oplus\)操作符
现实世界的系统通常是由一些外在的输入驱动的。为了模拟这一现象,除了描述流形本身所在的状态之外,还需要一个额外的操作来描述流形上的状态是如何在无限小的时间周期内由恒定的外生速度驱动的。
尽管速度对状态的影响增加了对流形上其原始位置的扰动,这在流形上有很好的描述运算符\(\boxplus\),则外部速度不一定在相同的homeomorphic空间(即,切线空间)中,该空间定义操作,因此需要表示为\(\oplus_{\mathcal{M}}\)的新操作。
假设外部速度的维度是l,那么新的操作为:\(\oplus_{\mathcal{M}}: \mathcal{M} \times \mathbb{R}^{l} \mapsto \mathcal{M}\)
具体地说,当\(\mathcal{M}\)是李群时,外生速度通常位于正切空间,同时也定义了公式(2)中的\(\boxplus \backslash \boxminus\)操作,因此操作⊕与\(\boxplus\)重合,即:
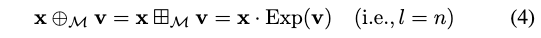
。。。
差分
\((((\mathbf{x} \boxplus \mathbf{u}) \oplus \mathbf{v}) \boxminus \mathbf{y})\)相对于\(\mathbf{u}\)和\(\mathbf{V}\)的差分将会在后面的卡尔曼滤波器中用到,其中,\(\mathbf{x}, \mathbf{y} \in \mathcal{M}, \mathbf{u} \in \mathbb{R}^{n}\),\(\mathbf{v} \in \mathbb{R}^{l}\)。
由链式法则,可得:

对于某些流形(例如,SO(3)),计算微分通常更为方便,而不用使用链式法则展开。
复合可微流形
基于流形的笛卡儿积原理,给出了流形的定义由两个子流形(归纳为任意个子流形)组成的复合流形上的\(\boxplus \backslash \boxminus\) and \(\oplus\)操作定义如下:

因此复合流形上的偏微分满足(见引理):
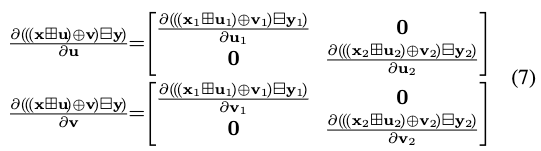
\(\boxplus \backslash \boxminus\) and \(\oplus\)运算及其在复合流形上的偏微分非常有用,使用户能够定义\(\boxplus \backslash \boxminus\) and \(\oplus\)运算及其导数(例如,\(\mathbb{R}^{n}, S O(3), \mathbb{S}^{2}(r)\)),然后将这些定义推广到更复杂的复合流形。
例如,根据前面讨论\(\boxplus \backslash \boxminus\) and \(\oplus\)的定义,总结了几个重要流形,包括\(\mathbb{R}^{n}, S O(3), \mathbb{S}^{2}(r)\)的运算,并在表中总结了它们的局部微分,其中:
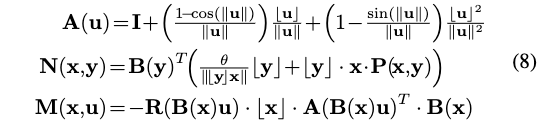
其中,\(\lfloor\mathbf{u}\rfloor\)记为反对称矩阵,并且有:
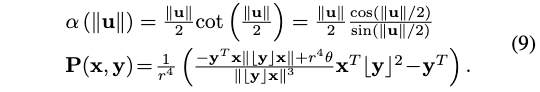
总结表如下: (详细推导见附录B)
